Cím:	1960. évi fizika OKTV feladatai
Füzet:	1960/október, 81 - 90. oldal	PDF  |  MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az I. forduló feladatai   1. Szabadon álló ház helyiségeinek $20{\text{C}}^{\circ }$-on való tartására egy fűtési idény alatt $50q$ szén szükséges. A ház hőleadása olyan, hogy a mennyezeten keresztül $30\%$-a, az oldalfalakon keresztül pedig $70\%$-a távozik a hőnek. A külső levegő átlaghőmérséklete az egész fűtési idény alatt $5{\text{C}}^{\circ }$. Mennyi tüzelőmegtakaritás érhető el, ha az oldalfalak vastagságát megkétszerezzük? Mennyi a szükséges tüzelőmennyiség mindkét esetben, ha a külső levegő átlaghőmérséklete a fűtési idény alatt $2{\text{C}}^{\circ }$, a belső hőmérsékletet viszont továbbra is $20{\text{C}}^{\circ }$-on tartjuk?   Megoldás: A ház eredeti állapota és az eredeti hőmérsékletadatok mellett az $50\text{<span style="font-weight: normal;font-style: normal;">q</span>}$ $30\%$-ának, azaz $15\text{<span style="font-weight: normal;font-style: normal;">q</span>}$ szén által termelt hőnek a menyezeten, a $70\%\left(35\text{<span style="font-weight: normal;font-style: normal;">q</span>}\right)$ szén által termelt hőnek a falakon át kell távoznia. Az összes szénfogyasztás $15+x-35=50\text{<span style="font-weight: normal;font-style: normal;">q</span>}$. Ha az oldalfalakat megvastagítjuk, ezeken át fele annyi hő távozik, mint előbb, vagyis csak $17\mathrm{,}5\text{<span style="font-weight: normal;font-style: normal;">q</span>}$ szén által termelt hő. Az összes szénfogyasztás $15+17\mathrm{,}5=32\mathrm{,}5\text{<span style="font-weight: normal;font-style: normal;">q</span>}$. Ha a külső hőmérséklet $5{\text{<span style="font-weight: normal;font-style: normal;">C</span>}}^{\circ }$ helyett $2{\text{<span style="font-weight: normal;font-style: normal;">C</span>}}^{\circ }$ akkor a hőmérsékletkülönbség ${15}^{\circ }$ helyett ${18}^{\circ }$ és így az egyébként változatlan körülmények között távozó hőmennyiségek $\frac{18}{15}=\frac{6}{5}$ arányban nagyobbak. Ennyiszer több szenet kell használni. Az első esetben a szénmennyiség $60\text{<span style="font-weight: normal;font-style: normal;">q</span>}$, $\left(18+42\right)$, a második esetben, dupla falaknál $39\text{<span style="font-weight: normal;font-style: normal;">q</span>}$, $\left(18+21\right)$.   2. 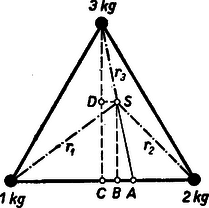$1\text{kg}$, $2\text{kg}$, illetőleg $3\text{kg}$ tömeg egymástól 1‐1 $\text{m}$ távolságra egyenlőoldatú háromszög csúcspontjaiban helyezkedik el. A rendszer a saját súlypontján keresztülmenő, a háromszög síkjára merőleges tengely körül másodpercenként $2$ fordulattal egyenletesen forog. Mennyi a rendszer forgási energiája? (A tömegeket tartó merev szerkezet tömege elhanyagolható.)   Megoldás: Először meg kell határoznunk a súlypont helyzetét. Az 1 kg és 2 kg közös súlypontja $A$-ban van, az 1 kg-tól $\frac{2}{3}$ méterre, a 2 kg-tól $\frac{1}{3}$ méterre. Az $A$-ban egyesített 3 kg és a háromszög harmadik csúcsában levő 3 kg közös súlypontja e távolság felezőpontjában, $S$-ben van.     A súlypont távolságai a tömegektől ($r_1$, $r_2$, $r_3$,) Pythagoras-tétellel számíthatók az $1BS$, $2SB$ és $3DS$ derékszögű háromszögekből, figyelembe véve, hogy $AB=\frac{1}{6}\text{<span style="font-weight: normal;font-style: normal;">m</span>}$, $AB=BC=\frac{1}{12}\text{<span style="font-weight: normal;font-style: normal;">m</span>}$, $BS=CD=3D=\frac{1}{2}\cdot \frac{\sqrt[]{3}}{2}\text{<span style="font-weight: normal;font-style: normal;">m</span>}$. A távolságok négyzetei: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle r_1^2=\frac{19}{36}\cdot {10}^4{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle r_2^2=\frac{13}{36}\cdot {10}^4{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle r_3^2=\frac{7}{36}\cdot {10}^4{\text{<span style="font-weight: normal;font-style: normal;">cm</span>}}^2\mathrm{.}}\hfill \end{array}}$ Az $\omega =2\pi n=2\pi \cdot 2=12\mathrm{,}56{\text{<span style="font-weight: normal;font-style: normal;">sec</span>}}^{-1}$ szögsebességgel történő forgáskor az egyes tömegek sebességei $v_1=\omega \cdot r_1$, $v_2=\omega \cdot r_2$, $v_3=\omega \cdot r_3$, és így az ergben kifejezett mozgási energia: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle E_{\text{<span style="font-weight: normal;font-style: normal;">m</span>}}}& {\displaystyle =\frac{1}{2}\cdot {10}^3\cdot r_1^2{\omega }^2+\frac{1}{2}\cdot 2\cdot {10}^3\cdot r_2^2{\omega }^2+\frac{1}{2}\cdot 3\cdot {10}^3\cdot r_3^2{\omega }^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\cdot {\omega }^2\cdot \left[{10}^3\cdot r_1^2+2\cdot {10}^3\cdot r_2^2+3\cdot {10}^3\cdot r_3^2\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\cdot 157\mathrm{,}8\cdot \left[{10}^7\cdot \frac{19}{36}+2\cdot {10}^7\cdot \frac{13}{36}+3\cdot {10}^7\cdot \frac{7}{36}\right]=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{1}{2}\cdot 157\mathrm{,}8\cdot \frac{66}{36}\cdot {10}^7=144\mathrm{,}6\cdot {10}^7\text{<span style="font-weight: normal;font-style: normal;">erg</span>}=144\mathrm{,}6\text{<span style="font-weight: normal;font-style: normal;">joule</span>}=14\mathrm{,}8\text{<span style="font-weight: normal;font-style: normal;">mkp.</span>}}\hfill \end{array}}$ A zárójelben levő mennyiség a tehetetlenségi nyomaték. Ha ezt ismerjük, akkor kiszámíthatjuk a mozgási energiát a minden pontban közös szögsebesség felhasználásával anélkül, hogy az egyes részek sebességeit külön ki kellene számítani.   Megjegyzés. Valamely (a rajz síkjára merőleges) tengely körüli forgás esetében akkor a legkisebb a tehetetlenségi nyomaték és adott fordulatszám mellett a mozgási energia, ha a tengely átmegy a súlyponton. Próbáljuk a rendszert más tengely, például a háromszög valamely csúcsán átmenő tengely körül forgatni: nagyobb lesz a tehetetlenségi nyomaték és a mozgási energia.   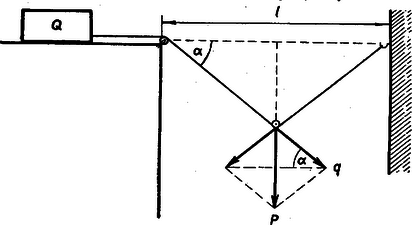3. Egy épület vízszintes, lapos tetején levő $300\text{kg}$ tömegű homokládához erősített kötelet a tető felett vízszintesen vezetjük, majd az épület széléhez erősített állócsigán vetjük át. A kötelet, még ráfűzve egy mozgócsigát, a szemben levő épületen egy vízszintes kötélrésszel a tetővel egy magasságban, az állócsigától $10\text{m}$ távolságban rögzítjük. A két épület között elhelyezett állványról a $10$ méteres szakasz közepére helyezett mozgócsigára $50\text{kg}$-os terhet akasztunk és a vízszintes kötélállásban nyugvó rendszert elengedjük. A belógó kötél milyen állásánál lesz egyensúly, ha a vízszintes tetőn a súrlódási együttható $1/6$-nak vehető? ‐ Milyen messzire kell lennie a ládának az álló csigától, hogy a végül létrejövő egyensúlyi helyzetben a láda még ne érje el az állócsigát? (A csigák méretei, a kötél és a csigák súrlódása, a közegellenállás elhanyagolható.)   Megoldás. A láda súlya $Q$ kp, a csigán lógó teher súlya $P$ kp. Amikor a kötél $\alpha$ szöggel hajlik le, akkor a $P$ súly kötelet feszítő összetevője $q=\frac{P}{2\text{sin}\alpha }$. Az a legnagyobb súrlódási erő, amely a láda fenekén létrejöhet: $\mu Q$, ($\mu$ a súrlódási együttható). Amikor a kötél még majdnem vízszintes egyenes, akkor $q$ igen nagy, feltétlenül nagyobb, mint a súrlódási erő, így a láda feltétlenül elindul. Ha a ládát kézzel fogjuk és nem engedve meglódulni lassan vezetjük, akkor addig megy tovább, amíg a kötelet feszítő erő egyenlő nem lesz a súrlódási erővel. Ebben a sztatikus egyensúlyi helyzetben $\begin{array}{c}{\displaystyle \frac{P}{2\text{sin}{\alpha }_0}=\mu Q\mathrm{,}}\end{array}$ Ezért a sztatikus egyensúly feltétele: $\begin{array}{c}{\displaystyle \text{sin}{\alpha }_0=\frac{P}{2\mu Q}\mathrm{.}}\end{array}$ Tehát lassan, fékezve csúszó láda esetében a láda és a mozgócsiga akkor áll meg, amikor a lehajló kötél ${\alpha }_0$ szöget zár be a vízszintessel. A mi adatainkkal $\text{sin}{\alpha }_0=0\mathrm{,}5$ és ${\alpha }_0={30}^{\circ }$.     Azonban feladatunkban arról van szó, hogy nem fékezzük a ládát, hagyjuk hogy felgyorsuljon, szabadon mozogjon. Ebben az esetben kérdezzük, meddig süllyed le $P$ súly és mennyit mozdul el a láda? A mozgás lefolyását nehéz volna számítással végig kísérni, azonban a végső helyzetet meghatározhatjuk az energiamegmaradás törvényével. A mozgási energia a kísérlet előtt és után nulla. $P$ súly lesüllyedésével helyzeti energiát veszít, ami súrlódás által hővé lesz a láda fenekén. Ha a láda valamilyen (végső) $\alpha$ kötélállás mellett áll meg, akkor $P$ lesüllyedése, $\frac{l}{2}\cdot \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha$ és a helyzeti energia csökkenése $\frac{l}{2}\cdot \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \cdot P$. A láda elmozdulása $2\cdot \left(\frac{l}{2\text{cos}\alpha }-\frac{l}{2}\right)=l\left(\frac{1}{\text{cos}\alpha }-1\right)$. Ugyanis a kötél által alkotott egyenlőszárú háromszög szára $\frac{l}{2\text{cos}\alpha }$, az egyenlőszárú háromszög alapjának fele $\frac{l}{2}$, tehát ennyivel hosszabb a szárak összege, mint az alap, vagyis ennyi kötélnek kellett az álló csigán átgördülnie. A $\mu Q$ súrlódási erő ellen végzett munka $\mu Ql\left(\frac{1}{\text{cos}\alpha }-1\right)$. Ezen nem változtat az a körülmény, hogy a mozgás folyamán a ládát húzó erő nem állandó, mert súrlódással hővé csak az a munka alakul, amelyet $\mu Q$ erő végez. A húzóerő többlete a mozgás elején gyorsítja a ládát, de a mozgás vége felé, amikor ${\alpha }_0$-t túltéptük, a húzóerő kisebb, mint a súrlódási erő; ekkor a ládát a lendület viszi tovább, amíg le nem fékeződik. Végeredményben mégis csak $\mu Ql\left(\frac{1}{\text{cos}\alpha }-1\right)$ a súrlódás ellen végzett munka. Ezt egyenlővé tesszük a helyzeti energia csökkenésével: $\begin{array}{c}{\displaystyle \mu Ql\left(\frac{1}{\text{cos}\alpha }-1\right)=\frac{l}{2}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \cdot P\mathrm{.}}\end{array}$ Ez egyenlet $\alpha$ számára. A $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{\sqrt[]{1-\text{cos}{}^2\alpha }}{\text{cos}\alpha }$ helyettesítéssel, négyzetre emeléssel és rendezéssel kapjuk az eredményt: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{1-{\left(\frac{P}{2\mu Q}\right)}^2}{1+{\left(\frac{P}{2\mu Q}\right)}^2}\mathrm{.}}\end{array}$ Felhasználhatjuk itt a $\text{sin}{\alpha }_0=\frac{P}{2\mu Q}$ röviditő jelölést: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{1-\text{sin}{}^2{\alpha }_0}{1+\text{sin}{}^2{\alpha }_0}\mathrm{.}}\end{array}$ Számértékeinket felhasználva $\text{cos}\alpha =0\mathrm{,}6$, $\alpha ={53}^{\circ }08\text{'}$. Eredményünk feltárja a sztatikus feladat ${\alpha }_0$ és a dinamikusan értelmezett feladat $\alpha$ eredményének összefüggését. Eredményünket a $\text{sin}\alpha =\sqrt[]{1-\text{cos}{}^2\alpha }$ azonosságba helyettesítve kapjuk: $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{2}{1+\text{sin}{}^2{\alpha }_0}\cdot \text{sin}{\alpha }_0\mathrm{.}}\end{array}$ Látható, hogy $\alpha$ feltétlenül nagyobb, mint ${\alpha }_0$, mert a $\frac{2}{1+\text{sin}{}^2{\alpha }_0}$ szorzó nagyobb 1-nél. A ládának az állócsigától mért legrövidebb távolsága $l\left(\frac{1}{\text{cos}\alpha }-1\right)=6\mathrm{,}67\text{<span style="font-weight: normal;font-style: normal;">m</span>}$. A kísérlet tényleges elvégzését valószínűleg nagyon befolyásolja, hogy a súrlódási együttható a valóságban nagymértékben függ a tárgy sebességétől.   A II. forduló feladatai   1. Szorosan illeszkedő, egymásba tolt tömör rézhengert és vascsövet két végén összehegesztettek. A rézhenger $10\text{mm}$ átmérőjű. Hogyan kellett megválasztani a vascső külső méreteit ahhoz, hogy a rendszer hosszanti hőtágulási tényezője a réz és a vas hőtágulási tényezőjének számtani középértéke legyen igen kis hőmérséklet-emelkedésnél? (A vas nyújtási modulusa $21000$, a rézé $12000\text{ kp/m<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$.)   Megoldás: Jelöléseink legyenek: (A nyújtási modulus a nyújtási rugalmassági együttható reciprok értéke.) A két rúd, illetve cső $0^{\circ }$-on, $l_0$ kezdeti hossz mellett van összehegesztve és a melegítés $t^{\circ }$-ra történik. Foglalkozzunk rögtön azzal az általánosabb esettel, amikor a kettős rúd tényleges $\alpha$ hőkiterjedési együtthatója a következő módon tevődik össze a két fém hőkiterjedési együtthatójából: $\begin{array}{c}{\displaystyle \alpha =m{\alpha }_1+n{\alpha }_2\mathrm{,}}\end{array}$ ahol $m+n=1$. Számtani közép esetében $m=n=0\mathrm{,}5$.     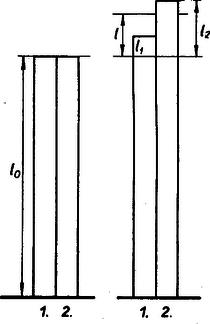Ha a rudak nem volnának összehegesztve, akkor a hőkiterjedések volnának a vasnál $l_1={\alpha }_1{l}_{0}t$, a réznél $l_2={\alpha }_2{l}_{0}t$. Azonban e kettő közötti $l$ közös megnyúlás jött létre. A réz a vasat felhúzta $l-l_1$ darabbal, a vas a rezet visszahúzta $l_2-l$ darabbal. Ezekre a hosszváltozásokra Hooke törvénye érvényes: $\begin{array}{c}{\displaystyle l-l_1=\frac{{\epsilon }_1{l}_{0}P}{F_1}\mathrm{,}{l}_2-l=\frac{{\epsilon }_2{l}_{0}P}{F_2}\mathrm{.}}\end{array}$ A megoldás alapja, hogy ezek a hosszváltozásból származó erők egyenlők. Kifejezzük ezeket az erőket: $\begin{array}{c}{\displaystyle P=\frac{\left(l-l_1\right)F_1}{{\epsilon }_1{l}_0}\mathrm{,}P=\frac{\left(l_2-l\right)F_2}{{\epsilon }_2{l}_0};}\end{array}$ azután az erőket egyenlővé tesszük: $\begin{array}{c}{\displaystyle \frac{\left(l-l_1\right)F_1}{{\epsilon }_1{l}_0}=\frac{\left(l_2-l\right)F_2}{{\epsilon }_2{l}_0}\mathrm{.}}\end{array}$ A megnyúlások helyébe betesszük a hőkiterjedési törvényből következő értékeket, figyelembe véve, hogy a kettős rúd előírt a hőkiterjedési együtthatójának jelentése szerint $l=\alpha l_{0}t$, $\begin{array}{c}{\displaystyle \frac{\left(\alpha l_{0}t-{\alpha }_1{l}_{0}t\right)F_1}{{\epsilon }_1}=\frac{\left({\alpha }_2{l}_{0}t-\alpha l_{0}t\right)F_2}{{\epsilon }_2}\mathrm{,}}\end{array}$ $t$ és $l_0$ kiesik. Feladatunk ismeretlene az $\frac{F_1}{F_2}$ keresztmetszetarány. Ezt kifejezzük: $\begin{array}{c}{\displaystyle \frac{F_1}{F_2}=\frac{{\epsilon }_1}{{\epsilon }_2}\cdot \frac{{\alpha }_2-\alpha }{\alpha -{\alpha }_1}\mathrm{.}}\end{array}$ Most gondoljunk arra, hogy előírásunk szerint $\alpha =m{\alpha }_1+n{\alpha }_2$, $\begin{array}{c}{\displaystyle \frac{F_1}{F_2}=\frac{{\epsilon }_1}{{\epsilon }_2}\cdot \frac{{\alpha }_2-m{\alpha }_1-n{\alpha }_2}{m{\alpha }_1+n{\alpha }_2-{\alpha }_1}\mathrm{.}}\end{array}$ Azonban $m$ és $n$ nem függetlenek egymástól: $n=1-m$ és $m=1-n$. Ezt felhasználva: $\begin{array}{c}{\displaystyle \frac{F_1}{F_2}=\frac{{\epsilon }_1}{{\epsilon }_2}\cdot \frac{{\alpha }_2-m{\alpha }_1-\left(1-m\right){\alpha }_2}{\left(1-n\right){\alpha }_1+n{\alpha }_2-{\alpha }_1}=\frac{{\epsilon }_1}{{\epsilon }_2}\cdot \frac{m{\alpha }_2-m{\alpha }_1}{n{\alpha }_2-n{\alpha }_1}=\frac{{\epsilon }_1}{{\epsilon }_2}\cdot \frac{m}{n}\mathrm{.}}\end{array}$ Igen érdekes, hogy a hőkiterjedési együtthatók kiesnek és a keresztmetszet területek arányát a nyújtási rugalmassági együtthatók aránya adja meg, mindegyiket megszorozva (súlyozva) azzal a törttel, amellyel az illető anyag hőkiterjedési együtthatója szerepel a közös hőkiterjedési együtthatóban. Feladatunkban $\frac{m}{n}=\frac{0\mathrm{,}5}{0\mathrm{,}5}=1$, $\frac{{\epsilon }_1}{{\epsilon }_2}=\frac{1:21000}{1:12000}=\frac{4}{7}$, tehát  $\frac{F_1}{F_2}=\frac{4}{7}$. Mivel $F_1=\pi \cdot 5^2{\text{<span style="font-weight: normal;font-style: normal;">mm</span>}}^2$, $F_2=\frac{7}{4}\cdot \pi \cdot 5^2{\text{<span style="font-weight: normal;font-style: normal;">mm</span>}}^2$, az együttes rúd keresztmetszet területe $F_1+F_2=\frac{11}{4}\cdot \pi \cdot 5^2$. Legyen az együttes rúd külső felületének rádiusza $r$, ekkor $\pi r^2=\frac{11}{7}\cdot \pi \cdot 5^2$, $r=\frac{5}{2}\sqrt[]{11}\text{<span style="font-weight: normal;font-style: normal;">mm</span>}$, a külső átmérő $2r=5\sqrt[]{11}=16\mathrm{,}56\text{<span style="font-weight: normal;font-style: normal;">mm</span>}$.   Azért kell kis hőfok különbségre szorítkoznunk, mert csak kis méretváltozásoknál egyezik a nyújtás és összenyomás Hooke-törvényének együtthatója, azonkívül mind a hőkiterjedési-, mind a Hooke-tőrvény szigorúan csak elég kis változásokra érvényes. Ha $a_2=a_1$, akkor az $a_2-a_1$-gyel történő egyszerűsítés helytelen. Valóban egyenlő hőkiterjedési anyagokból készült kettős rúd hőkiterjedési együtthatója a keresztmetszet területektől függetlenül azonos a két összetevő hőkiterjedési együtthatójával.   2. Egy egyenletesen tekercselt rugót a ráakasztott $m=1\text{kg}$ tömegű test súlya $\Delta l$ hosszúsággal nyújt meg $\text{g=981 <span style="font-weight: normal;font-style: normal;"><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>c</mi><mi>m</mi><mi>s</mi><mi>e</mi><mi>c</mi></mrow><mrow><mo stretchy="false">-</mo><mn>2</mn></mrow></msup></mrow></math></span>}$ mellett. A rugó egyik végéhez $m_1=1\text{kg}$, másik végéhez $m_2=2\text{kg}$ tömeget erősítettek és a szerkezetet kifeszített állapotban egy rakétában kilőtték. A rakéta szabadon repülő állapotában a rendszert kioldják. Mekkora lesz a tömegek rezgési ideje, ha a rugó tömege elhanyagolható?   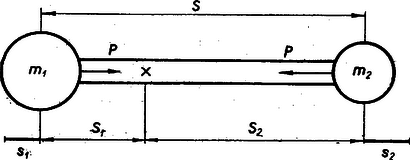Megoldás: Először csak a rezgés problémáját vizsgáljuk, azután térünk majd rá a rakétában való kilövés kérdésére. Rezgő rendszerünk jobb elképzelés szerint egy vastag, $S$ hosszúságú gumirúdból áll, amelynek végein $m_1$ és $m_2$ tömegek vannak. Elmegyünk olyan messze a Földünktől, hogy $m_1$ és $m_2$ tömegek súlya ne számítson. Ha a tömegeket távolabb húzzuk egymástól, a rugalmas erő visszaviszi a tömegeket eredeti helyzetük felé, majd a tehetetlenség következtében azon túlfutnak, a gumirudat összenyomják és rugalmas rezgés keletkezik. Keressük ennek a rezgésidejét. ,,Belső erők hatására a rendszer súlypontja továbbra is nyugalomban marad, rezgés közben nem mozdul el, akár meg is rögzíthető.'' (Párkányi László dolgozatából.)     A tömegek súlypontjainak távolságai fordítva arányosak a tömegekkel, $\begin{array}{c}{\displaystyle S_1:S_2=m_2:m_1\mathrm{.}}\end{array}$ Ha a tömegek széthúzásakor, a rugó megnyújtásakor ügyelünk arra, hogy a súlypont ugyanott maradjon, akkor $s_1$ és $s_2$ megnyúlásoknak is az $S_1$, $S_2$ arányában kell állniok, vagyis: $\begin{array}{c}{\displaystyle s_1:s_2=S_1:S_2=m_2:m_1\mathrm{.}}\end{array}$ Hooke törvénye szerint ugyanazon erőnél (ugyanazon rúdnál) a megnyúlások arányosak az eredeti hosszakkal. Aránypárunk éppen ezt jelenti, ezért a két tömegre ható rugalmas erőknek egyenlőknek kell lenni (Newton III. axiómájával is megegyezésben). A rezgő mozgás törvénye szerint az erő arányos az úttal: $m{\omega }^{2}s=P$, itt $\omega =\frac{2\pi }{T}$ tartalmazza $T$ rezgésidőt. A keletkező rezgés rezgésideje: $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{m\cdot \frac{s}{P}}\mathrm{.}}\end{array}$ Kiszámítjuk mindegyik tömeg rezgésidejét. $\begin{array}{c}{\displaystyle T_1=2\pi \sqrt[]{m_1\cdot \frac{s_1}{P}}\mathrm{,}{T}_2=2\pi \sqrt[]{m_2\cdot \frac{s_2}{P}}\mathrm{.}}\end{array}$ A fordított arányból következően $m_1{s}_1=m_2{s}_2$ tehát mindegyik tömeg rezgésideje ugyanaz, ami nélkül a súlypont állandó helyzete sem volna elképzelhető. Mivel $s_1+s_2=s$ a rugó teljes megnyújtása, és $s_1:s_2=m_2:m_1$, ezért $\begin{array}{c}{\displaystyle s_1=\frac{m_2}{m_1+m_2}\cdot s\mathrm{,}{s}_2=\frac{m_1}{m_1+m_2}\cdot s\mathrm{.}}\end{array}$ A rezgésidők: $\begin{array}{c}{\displaystyle T_1=T_2=2\pi \sqrt[]{\frac{m_1{m}_2}{m_1+m_2}\cdot \frac{s}{P}}\mathrm{.}}\end{array}$ Adatainkat felhasználva $T=0\mathrm{,}164\sqrt[]{\Delta l}$, ($T$ sec-ban, $\Delta l$ cm-ben.)   Most következik a rakétában történő kilövés vizsgálata. Ha az egész szerkezet ki van lőve a nehézségi erőtérbe (rakétával együtt vagy anélkül), akkor a rakétában beáll a súlytalanság állapota. Ez azt jelenti, hogy a rakétában a tárgyak nem nyomják egymást, mert valamennyien esnek (ez pedig a súlyos és tehetetlen tömeg egyenlőségének következménye). A kifeszített rugónk mindegyik tömege is egyformán esik (ugyancsak a súlyos és tehetetlen tömeg egyenlősége következtében), ezért a kioldás pillanatában, minthogy egyformán esik mindegyik tömeg, a közöttük levő távolság, az $s$ megnyúlás is változatlan marad, tehát ugyanúgy, ugyanolyan rezgésidővel rezegnek, mint az előbb tárgyalt esetben. De nem feltétlenül minden körülmény között: ha a rendszer forog, bukdácsol, akkor megváltozik a rezgésidő a centrifugális és Coriolis-erő következtében. Ezt legjobban így láthatjuk be: ha a szerkezet a gumirúdra merőleges tengely körül megfelelő fordulatszámmal forog, akkor a kioldott rugó tömegeire ható centrifugális erő előidézheti azt, hogy a rugó kinyúlva marad és nem keletkezik rezgés. Ha a rugós szerkezet kioldása pillanatában a rakéta még tüzel, ez nem jelent változást abban az esetben, ha az elszabadulás pillanatában a tömegek párhuzamos, egyirányú sebességet kapnak.   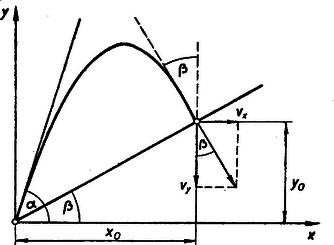3. Milyen szög alatt kell elhajítanunk egy testet, hogy az $\alpha$ hajítási pontból kiinduló $\beta ={20}^{\circ }$ hajlásszögű lejtőre esve, innen tökéletesen rugalmas ütközés után ugyanazon pályán térjen vissza kiindulási pontjába?   Megoldás: Az $\alpha$ szög alatt $c$ sebességgel elhajított tárgy pályájának függvénye: $\begin{array}{c}{\displaystyle y=\text{tg}\alpha \cdot x-\frac{\text{g}}{2c^2\text{cos}{}^2\alpha }\cdot x^2\mathrm{.}}\end{array}$ Itt $x$ és $y$ az elhajított tárgy koordinátái $t$ időpontban.     A $\beta$ hajlásszögű lejtő egyenesének függvénye $y=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta \cdot x$. A két függvényből álló egyenletrendszer ($x=0$-tól különböző) megoldása adja meg a lejtőre érkezés pontjának $x_0$ koordinátáját: $\begin{array}{c}{\displaystyle x_0=\frac{2c^2}{g}\cdot \text{cos}{}^2\alpha \left(\text{tg}\alpha -\text{tg}\beta \right)\mathrm{,}}\end{array}$ A becsapódásig eltelt idő: $\begin{array}{c}{\displaystyle t_0=\frac{x_0}{c\text{cos}\alpha }=\frac{2c\text{cos}\alpha }{\text{g}}\cdot \left(\text{tg}\alpha -\text{tg}\beta \right)\mathrm{,}}\end{array}$ mert a hajítás vízszintes, állandó sebességösszetevője $c\text{cos}\alpha$. Az elhajított tárgy visszatérésének feltétele, hogy a lejtőre rajzolt merőleges mentén történjen a becsapódás. Az elhajított tárgy sebességének összetevői: $\begin{array}{c}{\displaystyle v_x=c\text{cos}\alpha \mathrm{,}{v}_y=c\text{sin}\alpha -gt\mathrm{.}}\end{array}$ A mi esetünkben a becsapódási merőleges $\beta$ szöget alkot a függőlegessel és ezért $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{v_x}{-v_y}=\frac{c\text{cos}\alpha }{\text{g}{t}_0-c\text{sin}\alpha }\mathrm{.}}\end{array}$ Felhasználva $t_0$ időre kapott eredményünket: $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{c\text{cos}\alpha }{2c\text{cos}\alpha \left(\text{tg <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>α</mi></math>-<span style="font-weight: normal;font-style: normal;">tg</span> <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>β</mi></math>}\right)-c\text{sin}\alpha }=\frac{1}{2\left(\text{tg}\alpha -\text{tg}\beta \right)-\text{tg}\alpha }=\frac{1}{\text{tg}\alpha -2\text{tg}\beta }\mathrm{.}}\end{array}$ Ezt az egyenletet kell megoldanunk $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha$-ra: $\begin{array}{c}{\displaystyle \text{tg}\alpha =2\text{tg}\beta +\text{cotg}\beta \mathrm{.}}\end{array}$ Ez a képlet adja meg, hogy különböző $\beta$ hajlásszögű lejtők esetén mekkora a szög alatti elhajítás mellett pattan vissza a tárgy a kidobás helyére. Érdekes, hogy az elhajítás sebessége és $\text{g}$ nehézségi gyorsulás kiesnek. Feladatunk számadatai mellett, ha $\beta ={20}^{\circ }$, akkor $\alpha ={74}^{\circ }$. 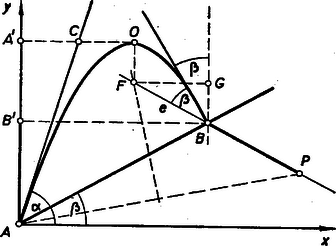(Mezei Ferenc dolgozatából.)     Bollobás Béla megoldása: Először szerkesztéssel keressük meg $\alpha$ szöget. $B$ becsapódási pontban a lejtő merőlegese $\beta$ szöget zár be a függőlegessel. Ugyanezt a $\beta$ szöget a másik oldalon mérve fel a merőlegestől olyan $e$ egyenest kell kapnunk, amely átmegy a parabola $F$ fókuszán, hiszen a parabola érintője felezi a fókuszhoz vezető és a direktrixre merőleges egyenesek szögét. Vetítsük $B$-t az $y$-tengelyre, kapjuk $B\text{'}$-t. $A$ pont $AB\text{'}$-vel van messzebb a direktrixtől, mint $B$ pont. De akkor $A$ pont a fókusztól számítva is $AB\text{'}$ darabbal van messzebb, mint $B$ pont. Egyenlítsük ki ezt az eltérést: mérjük rá $e$ egyenesre az $AB\text{'}=BP$ távolságot. Most már $P$ pont olyan messze van a fókusztól, mint $A$ pont. Ezek szerint a fókusz rajta van $AP$ merőleges felezőjén, valamint $e$ egyenesen is. Ezek metszéspontja adja meg $F$ fókuszpontot. Függőlegesen felette van a parabola $O$ csúcspontja. Helyét megkapjuk, ha az $FG$ távolság felét mérjük fel függőlegesen felfelé az $F$ ponttól. Az $OA\text{'}$ távolság $C$ felezőpontját $A$-val összekötve megkapjuk a kilövés $\alpha$ szögét. A szerkesztés menetéből levezethető az előbbi képletben kifejezett eredmény.   Kovács Béla megoldásában igen hasznosnak bizonyult az $x$-tengelynek a lejtőre való helyezése. Ezzel a számítás igen egyszerűvé vált. A kilövés szögét adja meg a lejtőhöz képest mért $\gamma$ szög, ekkor $\gamma =\alpha -\beta \cdot \gamma$ szöggel számolva a feladat megoldása ilyen egyszerű: $\begin{array}{c}{\displaystyle \text{tg}\gamma =\frac{1}{2}\text{cotg}\beta \mathrm{.}}\end{array}$ Megjegyzések: A feladatban kapott pálya azonos az 1956. évi Eötvös-verseny 1. feladatában szereplő pályával, amikor az volt a kérdés, hogy a lejtőn leguruló kocsiból hogyan kell úgy kilőni egy golyót, hogy az későbbi pályája folyamán eltalálja a kocsit.   Horváth Sándor (Bp., Rákóczi gimn. IV. o. t.) a Laphoz beküldött dolgozatában kimutatja, hogy a minimumon megy át, miközben $\beta 0^{\circ }$-ról ${90}^{\circ }$-ra növekszik. E minimumhoz tartozó értékek: $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta =\frac{\sqrt[]{2}}{2}$, $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =2\sqrt[]{2}$, $\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\gamma =\frac{\sqrt[]{2}}{2}$, $\beta =\gamma ={35}^{\circ }15\text{'}$, $\alpha ={70}^{\circ }30\text{'}$. Felhívjuk a figyelmet az ezzel a feladattal kapcsolatban levő, a Lap mai számában kitűzött feladatra!   Az 1960. évi országos középiskolai tanulmányi versenyen fizikából I. díjat nyert Párkányi László, a Budapest I. kerületi Petőfi g. IV. o. tanulója, II. díjat nyertek Bollobás Béla a Budapest V. kerületi Apáczai Csere g., Kovács Béla és Mezei Ferenc a Budapest II. kerületi II. Rákóczi Ferenc g. IV. o. tanulói. Dicséretet ill. könyvjutalmat nyertek a következő tanulók: Perjés Zoltán (Bp. VIII. Piarista g.), Zombori László (Bp. VIII. Vörösmarty g.), Balogh Zoltán (Bp. V. Apáczai Cs. g.), Elsner Gábor (Bp. I. Petőfi g.), Vatai István (Szolnok, Verseghy P. g.), Dobos László (Szeged, Radnóti g.), Farkas Henrik (Eger, Dobó g.), Gombkötő Mihály (Orosháza, Táncsics g.), Hammer Géza (Bp. I. Toldi F. g.), Jász Gábor (Bp. II. Rákóczi F. g.), Kiss Kálmán (Miskolc, Földes F. g.), Komlósi György (Szolnok, Verseghy g.), Máté Zsolt (Szeged, Radnóti g.), Pálfalvi György (Bp. VIII. Piarista g.), Poros Katalin (Bp. I. Szilágyi E. g.), Székely Jenő (Pécs, Nagy L. g.), Szűcs József (Szeged, Ságvári g.), Török Pál (Sárvár, Tinódi g.), Vámos Péter (Bp. III. Thán K. vegyipari techn.), Zajgóvári Károly (Bp. VIII. Piarista g.), Zólomy Imre (Sopron, Széchenyi g.).