Kezdőlap


Cím:	1959. évi Eötvös Loránd Fizikaverseny
Füzet:	1960/április, 149 - 152. oldal	PDF \| MathML
Témakör(ök):	Eötvös Loránd (korábban Károly Irén)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az Eötvös Loránd Fizikai Társulat minden év őszén versenyt rendez azok számára, akik abban az évben érettségiztek. A verseny ideje 5 óra és minden segédeszköz használható. Az 1959. évi Eötvös-verseny október 31-én folyt le. Ismertetjük a verseny feladatait és megoldásuk gondolatmenetét.

1. feladat: Vízzel telt nagy henger vízszintes helyzetű tengelye körül állandó szögsebességgel forog. A víz teljes mennyisége ugyanazzal a szögsebességgel mozog. A vízbe apró fémgolyót teszünk. A golyócska a víz forgása következtében nem süllyed a henger faláig, hanem a földhöz viszonyítva egyensúlyi helyzetben lebeg. Melyik körnegyedben helyezkedik el a fémgolyócska? (Megokolással). Állapítsuk meg pontosan a fémgolyócska helyét! (A közegellenállási erő dinben egyenesen arányos a golyó rádiuszával és a viszonylagos sebességgel, az arányossági szorzó

k = 0, 2

, ha a sebességet cm/sec-ban, a golyó rádiuszát cm-ben mérjük.) Mi történik fagolyó esetében? Felvehető számértékek: golyó rádiusza 1 mm, fémgolyó esetében a sűrűség

1, 7 g / c m^{3}

(magnézium), fagolyó esetében

0, 3 g / c m^{3}

, a szögsebesség

ω = 10 s e c^{- 1}

Megoldás: A

ϱ

rádiuszú,

d_{f}

sűrűségű,

V = 4, 19 ϱ^{3}

térfogatú,

q = 4, 19 ϱ^{3} d_{f}

tömegű golyó helyzetét

φ

szög és

r

távolság határozza meg. A golyóra három erő hat.

1. ábra

a) A súlyerő, amely a súly és az Archimedes törvényéből következő felhajtóerő különbsége. Ha a folyadék sűrűsége

d_{0}

, akkor ennek az erőnek a nagysága

q_{e} = 4, 19 ϱ^{3} (d_{f} - d_{0}) g

. Iránya fémgolyó esetében függőlegesen lefelé mutat.
b) A közegellenállási erő, amely arányos a víz

v = ω r

sebességével és az érintő irányában mutat; nagysága

P_{s} = k ϱ ω r

. (

k = 0, 2

az arányossági szorzó.)
c) A golyó tömegére nem hat centrifugális erő, mert a golyó nem mozog. A centrifugális erő nem a viszonylagos sebesség következménye, hanem a Földhöz, (valamely tehetetlenségi rendszerhez képest) létező sebesség következménye. Ellenben centrifugális erő hat a vízre és ez az erő a víz minden részecskéjét kifelé viszi. Kifelé vinné azt a vizet is, amelynek helyét a golyó foglalja el. Ezért, úgy mint a hidrosztatikában a felhajtóerő, itt a golyót körülvevő víz centrifugális ereje következtében a golyóra egy erő hat, amely a rádiusz mentén befelé, a középpont felé akarja elmozdítani és amelynek nagysága akkora, mint amekkora centrifugális erő hatna egy vízből álló golyócskára:

\begin{matrix} P_{c} = 4, 19 ϱ^{3} d_{0} ω^{2} r . \end{matrix}

A golyó akkor van egyensúlyban, ha e három erő eredője nulla. Az ábrából látható, hogy

tg φ = \frac{P_{c}}{P_{s}} = \frac{4, 19 ϱ^{3} d_{0}}{k ϱ} \cdot ω = \frac{4, 19 ϱ^{2} d_{0}}{k} \cdot ω

. Azonkívül

cos φ = \frac{P_{s}}{q_{e}} = \frac{k ϱ ω r}{4, 19 ϱ^{3} (d_{f} - d_{0}) g}

, innen

r = \frac{4, 19 ϱ^{2} (d_{f} - d_{0}) g cos φ}{k ω}

. Számadataink szerint

φ = 64^{\circ} 30'

és

r = 6, 185 cm

. A fagolyó az átellenes körnegyedben foglalna el szimmetrikus helyet.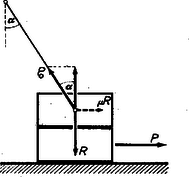

2. feladat: Vízszintes alapon egymáson fekszik két, egyenként

5

kilós tégla. A felső tégla, fedőlapjáról kiinduló fonállal egy állandó ponthoz van rögzítve. A fonál a függőlegessel

30^{\circ}

-os szöget zár be. A súrlódási együttható mindenütt

0, 2

. Mekkora erővel lehet az alsó téglát vízszintesen elhúzni?

Megoldás: A kötél a függőlegessel

α

szöget zár be. A fonálban ferdén felfelé

P_{0}

erő húz, a felső tégla az alsót

R

erővel nyomja.

2. ábra

Ez a két mennyiség az ismeretlen. A két ismeretlen meghatározásához szükséges két egyenlet a függőleges és vízszintes erők egyenlőségéből adódik. Ha

q

a tégla súlya és

μ

a súrlódási együttható, akkor igaz, hogy

P_{0}

vízszintes összetevője egyenlő a súrlódási erővel;

\begin{matrix} P_{0} sin α = μ R . \end{matrix}

Másrészt a felső téglát az alsóhoz szorító erőt megkapjuk, ha a felső tégla súlyából levonjuk a

P_{0}

fonálerő függőleges összetevőjét:

\begin{matrix} R = q - P_{0} cos α . \end{matrix}

Ennek az egyenletrendszernek a megoldása: (csak

R

-re van szükségünk)

\begin{matrix} R = \frac{q sin α}{sin α + μ cos α} . \end{matrix}

A leküzdendő súrlódási erő a húzott tégla felső oldalán

μ R

, az alsó oldalán

μ (q + R)

. Ezek összege a keresett teljes húzóerő:

\begin{matrix} P = μ R + μ (q + R) = μ q \frac{μ + 3 tg α}{μ + tg α} . \end{matrix}

Feladatunk számadataival

P = 2, 486 kgs

3. feladat: Helyezzünk el tőlünk nagy távolságban egy üvegkockát. Nézzük a kockát az alaplap átlójának meghosszabbításából. Mit látunk a kocka belsejében? (Törésmutató

1, 5

) Mit látunk, ha a kockát az asztalon elforgatjuk?

Megoldás: Vizsgáljuk rögtön azt az esetet, amikor a kocka elhelyezése nem szimmetrikus, és jobboldali oldallapja

ϵ

szöget zár be a felénk vezető fénysugarak irányával.

3. ábra

A messziről való nézés azt jelenti, hogy csak a kockából párhuzamosan kilépő fénysugarak lényegesek. Megfordítjuk a sugármenetet és a mi oldalunkról küldünk párhuzamos sugárnyalábot a kockára és azt keressük ezek fenn milyen módon hagynák el a kockát.
A kocka jobb alsó lapjához vezető párhuzamos sugarak egy része úgy megy át a kockán, mint párhuzamos falú üveglemezen. Ennek a sugárnyalábnak a szélessége

y

. A kocka oldallapjának

a

hosszúsága két részből tevődik össze:

\begin{matrix} \frac{y}{sin ϵ} + a \end{matrix}

Itt

δ

az üvegben létrejövő törési szög. Egyenletünkből

y = a sin ϵ (1 - tg δ)

. A töréstörvény szerint, ha

n

a törésmutató,

n = \frac{cos ϵ}{sin δ}

, ebből

tg δ = \frac{sin δ}{\sqrt[]{1 - sin^{2} δ}} = \frac{cos ϵ}{\sqrt[]{n^{2} - cos^{2} ϵ}}, és számításunk eredménye

\begin{matrix} y = a sin ϵ (1 - \frac{cos ϵ}{\sqrt[]{n^{2} - cos^{2} ϵ}}) . \end{matrix}

y

szélességű nyalábtól kifelé fekvő sugarak teljes visszaverődést szenvednek és, amint az ábrából könnyen megállapítható, baloldalt a kocka lapjához

ϵ

, a felénk tartó párhuzamos sugarak irányához képest

2 ϵ

szöggel haladnak.
A bal alsó oldalon kilépő, a kockán mint párhuzamos falú üveglemezen átment sugárnyaláb szélessége hasonló számítás alapján

x = a cos ϵ (1 - \frac{sin ϵ}{\sqrt[]{n^{2} - sin^{2} ϵ}})

. Az ennél kijjebb haladó sugarak most is teljes visszaverődéssel kerültek be a kockába, ezek a felénk tartó sugárnyaláb irányához képest fordítva felmért

2 ϵ

szöggel haladnak.
Tehát a kockába nézve a felénk mutató függőleges él két oldalán a kocka mögötti részeket látjuk, de felcserélve. Az éltől távolabb fekvő sávokban az oldalt fekvő teret látjuk teljes visszaverődés révén, ugyancsak felcserélve az oldalakat.
Abban az esetben, ha

n \leq \sqrt[]{2} cos ϵ

, a jobb oldalon kilépő nyaláb prizmaszerűen halad át a kockán. Ha

ϵ = 45^{\circ}

, a két oldalon látott képek szimmetrikusak.

Az Eötvös Loránd Fizikai Társulat az I. díjat nem adta ki. II. díjat nyert megosztva Tusnády Gábor (a sátoraljaújhelyi gimnáziumban Molnár Károly tanítványa) és Magos András (a budapesti II. Rákóczi Ferenc gimnáziumban Lantosy Károly tanítványa). III. díjat nyert Dániel Gábor (a budapesti piarista gimnáziumban Varga László tanítványa). Dicséretet kaptak Losonczi László (a miskolci Gábor Áron kohászati technikumban Schumann Sándor tanítványa), Szabó Gyula (a debreceni Fazekas Mihály gimnáziumban Nagy László tanítványa) és Tatai Péter (a budapesti I. István gimnáziumban Soós Károly tanítványa).