Kezdőlap


Cím:	A forgómozgásról. Impulzusnyomaték
Szerző(k):	Holics László
Füzet:	1960/április, 145 - 149. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bevezetés

A technikai civilizáció hajnalán történt hatalmas lépés, a kerék felfedezése és alkalmazása (kb. i. e. 4. évezredben) kinyitotta a kaput a mai értelemben vett technika szédületes fejlődése előtt. A forgómozgás a modern technikában rendkívül nagy szerepet játszik, szinte alig van mechanizmus, amely ne alkalmazna tengely körülforgó alkatrészeket. A forgó- és körmozgás (általában a centrális mozgások) nemcsak a technikai fejlődés bizonyos fokán lettek jelentősek, hanem a Világegyetemet alkotó anyag egyik legalapvetőbb fizikai mozgásformáját képviselik.
Az artista ellendül, többször megfordul a levegőben, majd pontosan talpra esik. A kerékpáros elengedi a kormányt, s biztonságosan halad, ha elég nagy a sebessége. Felpörögnek a lendkerekek és útjára indul az egysínű vasút. Hullámzik a viharos tenger és mégsem billeg a rajta úszó hajó. A pörgettyűs iránytű pontosan mutatja az irányt a repülőgép acéltömegei között. Forgózsámolyon pörgő tanuló összehúzza a széttárt karjait, s felgyorsul a forgása, mintha láthatatlan szerkezet perdítette volna meg. Búgócsigával játszó gyermek csodálkozva látja, amint az egy pontban alátámasztott test egyensúlyt tart. A bolygó vezérsugara egyenlő idők alatt egyenlő területeket súrol. Kísérleti tények kimutatták az antineutrínó létezését, ami a neki megfelelő neutrínótól épp forgásának egy jellemzőjében különbözik.

A fenti, és még sok hasonló tény és jelenség mögött a forgómozgásra nagy átfogó törvényt kell keresnünk, amelynek érvényesülése szabályozza az anyag e mozgását a gyerekjátéktól kezdve a bolygómozgáson keresztül az elemi részek fizikájáig. Nagyon hasznos tehát, hogy a forgómozgással kicsit behatóbban foglalkozzunk.

Egy újabb mennyiség. Még egy törvény

Ha megfigyeljük egy forgó kődarab mozgását, amelyet elhajítottunk, azt tapasztaljuk, hogy forgását és annak síkját is változatlanul, végig megtartja. Egy másik tapasztalat szerint toronyugró többszörös szaltó után úgy halad, ‐ esés közben forgássebességét belső,erőkkel ügyesen változtatva ‐ hogy mindig fejjel előre érkezzék a vízhez. Ezekről és még sok hasonló jelenségről a középiskolában tanult törvények nem képesek közvetlenül magyarázatot adni szükség van újabb fogalmakra és a forgó testek viselkedésének mélyebb vizsgálatára.
Bizonyára feltűnt az a,szembeszökő hasonlóság a haladó és forgómozgás között, amely abban nyilvánul meg, hogy mindkét területen léteznek egymásnak következetesen megfelelő mennyiségek, amelyek egymás szerepét betöltve a rájuk vonatkozó törvényeket (képleteket), megfelelő átírással megadják. (Pl.

m \sim I

ν \sim ω

s \sim α

, és ugyanakkor

E =^{1} /_{2} m v^{2} \to E =^{1} /_{2} I ω^{2}

, vagy

v = s / t \to ω = α / t

stb.) A haladó és forgómozgás közti párhuzamot a középiskolai tananyagban nem vittük végig a haladó mozgásnál tanult összes fogalomra. Most épp ezt akarjuk kiegészíteni.
A haladó mozgás útját megfeleltettük a körmozgás (forgómozgás) szögelfordulásának, az időt önmagának, a sebességet az újonnan definiált szögsebességnek, a vonalmenti gyorsulást a szöggyorsulásnak, a tömeget a tehetetlenségi nyomatéknak, az erőt a forgatónyomatéknak s ekkor a rájuk vonatkozó egyenletek közötti megfeleltetés végig helyesen adódott. Nem kerestük azonban a haladó mozgás mozgásmennyiségének megfelelőjét. Amint látni fogjuk, épp ebben rejlik a fenti megfigyelések magyarázata, szigorú leírása.
Az új mennyiség felismeréséhez induljunk ki a következő kísérletből. Közös (pl. függőleges) tengelyen, tetszőlegesen, súrlódás nélkül elfordulhat két, egymás fölött bizonyos távolságra levő korong. Az egyiknek

I_{1}

, a másiknak

I_{2}

a tehetetlenségi nyomatéka. Az alsó korongon egy ember áll, és a felső korongra, annak egy pontjában erőt fejt ki, amelynek hatására mindkét korong egymással ellentétes értelemben elfordul. (Ember helyett képzelhetünk egy összenyomott állapotban tartott rugót is, amelyik elengedés után elforgatja egymáshoz képest a két korongot. L. 1. ábrát).

1. ábra

Kövessük számítással a folyamatot, vizsgáljuk meg, mekkora szögsebességre tesznek szert a korongok külön-külön. E célból írjuk fel a mozgás tanult törvényeit.
Feltétlenül érvényes Newton III. törvénye, amely szerint

P_{12} = - P_{21}

Mivel az erő forgató hatására a forgatónyomaték jellemző, célszerű felírni:

\begin{matrix} F_{12} = - F_{21} \end{matrix}

ami szintén igaz, hiszen az erő karja értelemszerűen mindkét korongra nézve ugyanaz. A keresett szögsebességeket a fenti egyenletből tüstént kapjuk, ha felírjuk a forgatónyomatékok szöggyorsulásokkal kifejezett, jól ismert értékeit:

F = I β

és egyúttal az egyenlet mindkét,oldalát azzal a

t

idővel megszorozzuk, ameddig a kölcsönhatás tartott, s amely a III. törv. értelmében mindkét oldalra vonatkozóan ugyanaz az érték:

\begin{matrix} I_{1} β_{1} t = I_{2} β_{2} t, \end{matrix}

vagy

β_{1} t = ω_{l}

és

β_{2} t = ω_{2}

helyettesítéssel:

I_{1} ω_{1} = - I_{2} ω_{2}

. Innen a szögsebességekre kapjuk, hogy

I_{1} / I_{2} = - ω_{2} / ω_{1}

, vagyis a keletkező szögsebességek fordítottan arányosak a tehetetlenségi nyomatékokkal (és ellenkező irányúak)!
Ebből a tényből azonban egy sokkal általánosabb és fontosabb törvényt is ki tudunk olvasni az

I ω

jellegű mennyiségre vonatkozólag. Alakítsuk át ugyanis utolsó előtti egyenletünket nullára redukálva:

\begin{matrix} I_{1} ω_{1} + I_{2} ω_{2} = 0. \end{matrix}

Ha meggondoljuk, hogy az erőhatás előtt mindkét korong egymáshoz viszonyított szögsebessége 0 volt, az erőhatás előtti állapotra is igaz, hogy a tehetetlenségi nyomatékok megfelelő szögsebességekkel való szorzatainak összege nulla, azaz:

\begin{matrix} I_{1} 0 + I_{2} 0 = 0. \end{matrix}

Ezt úgy is megfogalmazhatjuk, hogy létezik a két forgó test rendszerére jellemző olyan

I ω

jellegű mennyiség, a következő összeg:

\begin{matrix} N \equiv I_{1} ω_{1} + I_{2} ω_{2}, \end{matrix}

(1)

amely értéke nem változik meg, ha a két test között belső forgatónyomatékok hatnak, például, ha a két testből álló rendszer zárt! Hiszen a fenti összegnek az erőhatás előtt is, utána is

0

az értéke, vagyis a belső forgatónyomatékok hatására olyan szögsebességek lépnek fel, hogy az

N = 0

egyenlet baloldalán szereplő (1) összeg a kölcsönhatás előtt is, után is 0 maradjon.
Ez a mennyiség tehát alá van vetve egy fontos törvénynek, amelyet az eddigi megmaradási törvényeink mellé kell sorolnunk. Máris szembeszökő e tételnek a mozgásmennyiség megmaradása tételével való nagy hasonlósága, sőt, levezetése lépésről lépésre megegyezik annak két testre való, elemi levezetésével. Rögtön láthatjuk, hogy ‐ amint azt várnánk ‐ az

I ω

jellegű mennyiség fog megfelelni formális átírással is a haladó mozgásnál szereplő mozgásmennyiségnek

(m v)

. Mielőtt ennek a mennyiségnek nevet adnánk, nézzük meg, milyen szorosabb kapcsolatban van a mozgásmennyiséggel. Egy általánosabb jellegű fogalom bevezetése után azonnal kiderül.

A nyomaték fogalma

Fizikában sokszor szerepel valamilyen vektor adott pontra vonatkozó nyomatékának a fogalma. Valamely tetszőleges vektornak adott 0 pontra vonatkozó nyomatékán értjük azt a vektort, amelynek 1) nagysága a vektor hosszának (absz. ért.) és hatásvonala 0 ponttól való távolságának szorzata, 2) iránya pedig merőleges az eredeti vektor és a 0 pont által meghatározott síkra, mégpedig úgy, hogy irányából visszanézve az eredeti vektor az óramutató járásával ellentétes (pozitív) irányba ,,forgat''.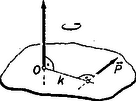

2. ábra

Ilyen módon definiált vektorral már találkoztunk eddig is. Hiszen az erőre alkalmazva a definíciót tengellyel rögzített testnél éppen a jól ismert forgatónyomatékot kapjuk (az erőnek a forgómozgásbeli megfelelőjét):

∣ \vec{F} ∣ = k \cdot ∣ \vec{P} ∣

, ahol

\vec{F} ⊥ k

és

\vec{P}

által meghatározott síkra. Az erő nyomatéka a forgatónyomaték. (A tehetetlenségi nyomaték nem ilyen értelmezésű, mert sem az, sem a tömeg nem vektort!)
Képezzük most a mozgásmennyiség nyomatékát adott tengely (pont) körül forgó anyagi pontnál. Mivel a körmozgásnál a sebesség és vele együtt a mozgásmennyiség minden pillanatban a sugárra merőleges (pályaérintő irányú) vektor, a mozgó ponthoz húzott sugár egyben a mozgásmennyiség hatásvonalának a forgásponttól való távolságát is adja. Így a mozgásmennyiség nyomatékának absz. értéke:

r \cdot m v

, ami a körmozgásnál szereplő szögadatokkal kifejezve:

r \cdot m v = r \cdot m ω r = m r^{2} ω

, ahol

m r^{2}

a pont

0

-ra vonatkozó tehetetlenségi nyomatéka, tehát:

\begin{matrix} r \cdot m v = I ω, \end{matrix}

vagyis a kísérletünkben olyan fontos szerepet játszó

I ω

jellegű mennyiség nem más, mint a mozgásmennyiség nyomatéka!

Ezt az egy pontra értelmezett vektort kiterjeszthetjük pontrendszerre (kiterjedt testre) is, mint az alábbi összeget:

\begin{matrix} \vec{N} \equiv I_{1} {\vec{ω}}_{1} + I_{2} {\vec{ω}}_{2} + ... + I_{n} {\vec{ω}}_{n} \equiv \sum_{i = 1}^{n} I_{i} {\vec{ω}}_{i}, \end{matrix}

ahol

I_{1} = m_{i} r_{i}^{2}

és

ω_{i} = a_{i} / t

(merev test esetén

ω_{1} = ω_{2} = ... = ω_{n}

). Jellege könnyen kiszámítható:

M L^{2} T^{- 1}

, egysége

gcm^{2}{sec}^{- 1}

és

kgm^{2}{sec}^{- 1}

. Vektor merőleges

r

és

m v

síkjára, azaz szögsebesség vektor irányú,

(\vec{N} = \vec{I ω})

, tehát a forgástengely irányába mutat (akár a forgatónyomaték). A fent levezetett tételt

\sum_{i = 1}^{n} I_{i} ω_{i} =

konstans általános alakban is megfogalmazhatjuk, és a mozgásmennyiség nyomatéka megmaradása tételének nevezzük.
Észrevehetjük a további összefüggéseket is. Ahogy a külső erő impulzusa megváltoztatja a rendszer mozgásmennyiségét, úgy a külső forgatónyomaték impulzusa (forgási impulzus, impulzusnyomaték) megváltoztatja a rendszer mozgásmennyiségének a nyomatékát. Ezek szerint a haladó mozgásnál szereplő impulzustételnek:

\begin{matrix} P = Δ m v / t, vagy P t = Δ m v \end{matrix}

(2a)

pontosan megvan a megfelelője, vagyis ha

r

-rel szorzunk (nyomaték):

\begin{matrix} F = Δ I ω / t, vagy F t = Δ I ω . \end{matrix}

(2b)

A (2a) képlet baloldalán az ún. impulzus szerepel, jobboldalán a mozgásmennyiség megváltozása. Az impulzus és mozgásmennyiség tehát általában nem azonos irányú és nagyságú vektorok, csak jellegük megegyező. Kizárólag egyenesvonalú mozgásnál, és ha a kezdősebesség

0

, igaz az, hogy az impulzus pillanatnyi értéke egyenlő a mozgásmennyiség pillanatnyi értékével. Az irodalom kissé felületes szóhasználattal azonban gyakran nem tesz különbséget az erő impulzusa és a test mozgásmennyisége között, s ilyen értelemben beszél a test impulzusáról is, az

m v

-t impulzusnak nevezve. Hasonlóképpen az

I ω

mennyiséget röviden impulzusnyomatéknak is nevezik (l. a címet). (A megmaradási elv nyilván az impulzusra és a mozgásmennyiségre is igaz.)

A (2a) összefüggéseket impulzustételnek, a (2b) alatti törvényt impulzusnyomaték tételének nevezzük.

Alkalmazás

Fenti tételeink speciális esete a következőképpen fogalmazható meg: Ha egy forgásba hozott tengelyhez rögzített, merev testet magára hagyunk, az megtartja egyenletes szögsebességű forgási állapotát mindaddig, amíg külső forgatónyomaték nem hat rá. (Külső forgatónyomaték származhat pl. súrlódó erőből is.) Hiszen ha

F = Δ I ω / t = 0

, akkor

I ω = const

, amiből következik, hogy ha a tehetetlenségi nyomaték

(I)

állandó (merev test), akkor a szögsebesség is állandó. Mivel az impulzusnyomaték vektor, melyet iránya is jellemez, a megmaradási tétel csak úgy lehet érvényben, ha annak sem nagysága, sem iránya nem változik meg. Mivel az

\vec{N} = \vec{I ω}

vektor a forgás síkjára merőleges, az iránytartás miatt következik, hogy a magára hagyott forgó test megtartja forgási síkját. (Forgó kő, pörgő búgócsiga, pörgettyűs iránytű stb.)
A másik típusú, magyarázatra szoruló jelenség: hogyan tudja belső erőkkel megváltoztatni forgó ember a szögsebességét?
Zárt rendszer esetén

I ω = const

. Eddig feltételeztük, hogy a test tehetetlenségi nyomatéka is állandó (merev test). Ez azonban nem szükségszerű: belső erőkkel könnyen meg tudjuk változtatni a tömegeloszlást (pl. összehúzódzkodással), aminek következtében a teh. nyom. is megváltozik. Ekkor tehát

I

és

ω

mennyiségek fordítottan arányosak, mert nem külön-külön állandók, hanem csak a szorzatuk az,

I ω = N

, vagy

I = N / ω

. Ha tehát a forgó ember hirtelen összehúzza magát, szögsebessége hirtelen megnövekszik. (Pl. ha felére csökken a teh. nyom., kétszeresére nő a szögsebesség.)

Kísérletek forgózsámollyal

A fentiek megértése után nézzünk néhány érdekes kísérletet, amit mindenki el tud végezni egy zongoraszék és egy ócska kerékpárkerék segítségével is. (A kerék abroncsát ajánlatos ólammal szegélyezni a nagyobb teh. nyom. elérése végett. Ezen kívül el kell látni a jó fogás számára egy tengellyel.)
1. A kísérletező személy feláll a forgózsámolyra, kezeibe vesz egy-egy 2 kp-os súlyt és kitárja karjait. Ezután valaki óvatosan megforgatja. Ha a forgó személy karjait összehúzza, a tehetetlenségi nyomaték lecsökkenése következtében a szögsebesség hirtelen megnő. (A magyarázat nem az energiamegmaradáson, hanem a mozgásmennyiség nyomatéka megmaradásán nyugszik.)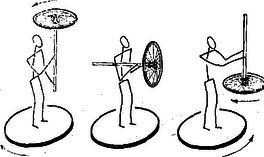

a) b) c)
3. ábra

Hajtsuk végre a 3/a, b, c ábrán közölt kísérleteket. a) Forgózsámolyon állva megforgatjuk a kereket: ellenkező irányban elindul a zsámoly. b) A forgó kerék tengelyét vízszintesre változtatjuk: a zsámoly forgása megszűnik. c) A forgó kerék tengelyét az első helyzethez képest

180^{\circ}

-ra állítva: a zsámoly forgása ellenkező irányba megindul. Magyarázat: a zsámoly-kerék rendszer összimpulzusnyomatéka kezdetben zérus. A kerék megforgatásakor keletkező többletimpulzusnyomatékot csak a zsámoly fent leírt mozgása tudja kompenzálni ellenkező irányú forgásából keletkező impulzusnyomatékkal.
3. Mi történik, ha a (2) alatt leírt helyzeteket úgy vesszük fel, hogy a kereket egy földön álló személy forgatta meg, majd úgy adta át a forgózsámolyon állá kísérletezőnek?