Cím: Az 1960. évi Arany Dániel tanulóversenyek II. fordulóján kitűzött feladatok megoldása, I. közlemény: A kezdők versenyének feladatai
Szerző(k):  Surányi János ,  Varga Tamás 
Füzet: 1960/november, 104 - 108. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. 41-nek a négyzete felírható úgy, hogy két ugyanannyi jegyből álló négyzetszámot (16 és 81) egymás után írunk. Írjunk a 41 jegyei közé valahány 9-est és a 9-esek után ugyanannyi 0-t. Bizonyítsuk be, hogy a keletkező számok négyzetének is mindig megvan a fenti tulajdonsága.

 

Megoldás: Néhány esetben az állítást könnyen igazolni tudjuk úgy, hogy elvégezzük a négyzetre emelést (akár csak szorzással is), az eredményt ,,kettévágjuk'', és mindkét részéből négyzetgyököt vonunk. Például:
412=1681,16=42,81=92,49012=24019801,2401=492,9801=992,4990012=249001998001,249001=4992,998001=9992.
A feladat állítása tehát azokban az esetekben, amikor egy vagy két 9-et és 0-t iktattunk közbe, helyes. Ezekből az esetekből úgy sejtjük, hogy a szóban forgó számok négyzetének két része nemcsak négyzetszám, (ami a feladat egyik állítása), hanem pontosan az első rész éppen a szóban forgó számok első felének négyzete, második részük pedig az eggyel több 9-esből álló szám négyzete, mint ahány 9-est közbeiktattunk.
Így van-e ez mindig ?
Képzeljük el, hogy n darab 9-est és utána n darab 0-t iktattunk a 4 és az 1 közé, ahol n bármely természetes szám. Így
49...9︸n+1jegy0...012︸n+1jegy=(49...9︸n+1jegy0...0︸n+1jegy+1)2=49...9︸n+1jegy0...02︸n+1jegy+2⋅49...9︸n+1jegy0...0︸n+1jegy+1.
Az összeg első tagjáról láthatjuk, hogy 2n+2 darab 0-ra végződik, és ezek előtt is van 2n+2 jegy, amelyek egybeolvasva éppen 49...9-nek a négyzetét adják. A megmaradó kéttagú összegről be akarjuk látni, hogy (10n+1-1)2-nel egyenlő. Ebből az is következni fog, hogy ez a szám csak 2n+2 jegyű (hiszen az első 2n+3 jegyű szám 10n+1-nek a négyzete, 102n+2), tehát nem nyúlik bele az előtte levő számba. A feladat megoldásához tehát csak annak igazolása hiányzik, hogy
(10n+1-1)2=2⋅49...9︸n+1jegy0...0︸n+1jegy+1.
A jobb oldalon álló számot így írhatjuk:
2(5⋅10n-1)⋅10n+1+1,
vagyis
10⋅10n⋅10n+1-2⋅10n+1+1,
azaz
102n+2-2⋅10n+1+1.
Ez pedig csakugyan egyenlő a bal oldali számmal.
 

Megjegyzés. A bizonyítást persze úgy is végezhettük volna, ha mindjárt az elején felírjuk algebrai alakban az n darab 9-es és n darab 0 közbeiktatásával kapott szám négyzetét:
[(5⋅10n-1)⋅10n+1+1]2,
elvégezzük a négyzetre emelést:
(5⋅10n-1)2⋅102n+2+2(5⋅10n-1)10n+1+1,
az összeg első tagjáról megállapítjuk, hogy négyzetszám, (5⋅10n-1)⋅10n+1-nek a négyzete, és a végén 2n+2 darab 0 van, a másik két tag összegéről pedig ‐ úgy mint az előbb ‐ megállapítjuk, hogy szintén négyzetszám, 10n+1-1-nek a négyzete, és mivel 2n+2 jegyből áll, nem nyúlik bele az előtte álló négyzetszámba, jegyei csak a 0-kkal adódnak össze. A bizonyítás általánossága azonban az előbb elmondott formában sem szenvedett csorbát, a kevesebb algebrai jelölés mögött jobban el lehet képzelni magukat a tízes számrendszerben felírt számokat.
 

2. feladat. Bizonyítsuk be, hogy egy szabályos ötszög két szomszédos csúcsán és az ötszög körülírt körének középpontján átmenő kör átmegy két átló metszéspontján is.
 

Megoldás: A bizonyításban az ábra jelöléseit vesszük alapul; csak az ott egy, ill. két ívvel jelölt szögekről lesz szó, ezért elég lesz a szögeket a csúcsuknál levő betűvel jelölni.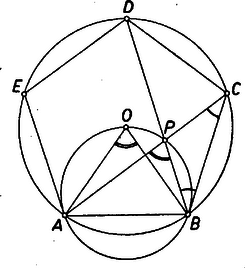
 

 

Be kell bizonyítanunk, hogy az A, B, és O ponton átmenő kör átmegy a P ponton is. Mint tudjuk (a kerületi szögekre vonatkozó tétel és megfordítása alapján) ez akkor és csak akkor igaz, ha O∢=P∢. De O∢=2C∢, tehát elég azt bizonyítanunk, hogy P∢=2C∢. P∢ viszont a PBC háromszög egyik külső szöge, tehát elég azt belátnunk, hogy C∢=B∢. Ez azonban nyilvánvaló, hiszen az ötszög szabályos, és így az AB^ és CD^ ívek, amelyeken ezek a szögek nyugszanak, egyenlők. Ezzel a bizonyítást befejeztük.
 

Megjegyzések. 1. Felhívjuk a figyelmet arra, hogy bár a bizonyítandó állításból indultunk ki, a továbbiakban nem azt vizsgáltuk, hogy ebből az állításból mi következik, hanem azt, hogy mi az, amiből ez következik.
2. Az ötszög szabályos voltából csak annyit használtunk ki a bizonyításban, hogy AB^ és CD^ a körnek két egyenlő, közös pont nélküli, egyező irányítású íve. Sőt, a bizonyítás kis módosítással kiterjeszthető arra az esetre is, amikor a két ívnek van közös pontja, akár közös ívdarabja is; csak azt kell kikötnünk, hogy az A, B, C és D pontok közül legalább három különböző legyen, mert különben AC és BD egy egyenesbe esik, és így metszéspontjukról nem beszélhetünk. Igaz tehát a következő állítás:
Ha AB^ és CD^ az O középpontú körnek két egyenlő és egyező irányítású íve (vagyis ha A-ból ugyanakkora abszolút értékű és ugyanolyan irányú forgás visz B-be, mint C-ből D-be), akkor az AC és a BD egyenes metszéspontja ‐ ha létezik ‐ rajta van az A, O és B pontokon átmenő kör kerületén.
 

3. feladat. Bizonyítsuk be, hogy bárhogyan választunk ki a 24-en aluli páratlan természetes számok közül 7 különbözőt, és képezzük belőlük az összes lehetséges különbségeket, van olyan szám, amely e különbségek között legalább háromszor fordul elő.
 

I. megoldás: 24-en alul 12 páratlan természetes szám van: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23. Ezek bármely kettője között a különbség (a nagyobból vonva le a kisebbet) pozitív páros szám és 2-től 22-ig minden páros szám előfordul különbségként.
Ha kiválasztunk hetet páratlan számaink közül, ezekből 21 pár képezhető és így 21 különbség lép fel (ismét mindig a nagyobból vonva ki a kisebbet).
Kíséreljük meg úgy választani ki a két számot, hogy a 21 különbség között a lehetséges 11 érték mindegyike legfeljebb kétszer forduljon elő. Be fogjuk látni, hogy ez lehetetlen. A követelmény teljesítéséhez minden esetre szükséges, hogy mind a 11 érték fellépjen a hét szám különbségei közt, mert ha kevesebb lépne fel, még ha mind elő is fordul kétszer, az is legfeljebb 20 értéket adna.
A legkisebb és legnagyobb szám különbsége nyilván nagyobb a többi 20 különbségnél, tehát csak egyszer lép fel a különbségek közt. Ennek tehát a lehetséges legnagyobb értéknek kell lennie, és a többi lehetséges értéknek mindnek kétszer kell fellépnie a 7 szám közti különbségek közt, mert még 20 különbség lép fel. A legnagyobb fellépő különbség tehát 22 lesz és ez csak úgy léphet fel, ha 1 és 23 szerepel a kiválasztott számok közt. Két kiválasztott számpár közt kell, hogy 20 legyen a különbség, ekkora különbséget azonban csak az 1 és 21, továbbá a 3 és 23 számok adnak. Így 3 és 21 is elő kell forduljon a hét kiválasztott szám között. Ezek különbsége, 18, még egy számpár között is fel kell, hogy lépjen. Ilyen számpár kettő van: az 1, 19 és az 5, 23. Azonban akár az 5, akár a 19 szerepel 1, 3, 21, 23-on kívül, a kiválasztott számok között, a 2 már háromszor lép fel mint különbség: az 1 és 3 továbbá a 21 és 23 számokon kívül a 3 és 5, ill. a 19 és 21 számok különbsége is 2. Nem lehetséges tehát a hét számot a kívánt módon kiválasztani. Ezzel a feladat állítása igazolást nyert.
Lényegében így oldotta meg a feladatot Kászonyi László (Szombathely, Nagy Lajos gimnázium).
 

Megjegyzések. 1. Többen azt állították, hogy a hét kiválasztott szám között 42 különbség lép fel, amelyek 11 féle értéket vehetnek fel. Ebből nyilvánvalóan következnék a feladat állítása, sőt az is, hogy van érték, amelyik négyszer is fel lép a különbségek közt. Hibás azonban az okoskodás, mert a fellépő különbségek közt a negatívakat is figyelembe veszi, a lehetséges különböző értékekként azonban csak a pozitívakat veszi számba. Az okoskodás helytelensége abból is látszik, hogy pl. az 1, 3, 7, 9, 17, 21, 23 számok különbségei közt egyetlen érték sem szerepel négyszer.
2. Voltak, akik beérték annak megállapításával, hogy néhány általuk felírt kiválasztás esetén találnak a különbségek közt legalább háromszor fellépő értéket. Ebből azonban nem következik semmi a további lehetséges kiválasztásokra. Az összes lehetséges (792) esetet végigpróbálgatni pedig igen fáradságos munka lenne.
 

II. megoldás: A hét kiválasztott számot rendezzük nagyság szerint sorba és vizsgáljuk a szomszédosak közt fellépő különbségeket. Ezek összege megadja a legkisebb és legnagyobb kiválasztott szám különbségét, tehát nem lehet nagyobb, mint 22. A tekintetbe vett különbségekként tehát hat pozitív páros számot kell keresnünk, amelyek összege nem nagyobb, mint 22. Ezek közt elő kell fordulnia a 2-nek, mert különben a hat szám összege legalább 6⋅4=24 volna. Ha további 5 szám 2-nél nagyobb, ez csak úgy lehet, hogy mind 4, tehát a 4 előfordul háromszor (többször is) a különbségek közt.
Tegyük fel most, hogy két különbség értéke 2. Ha a további különbségek közt is fellép még a 2, akkor ez az érték már legalább háromszor előfordul a különbségek közt. Ha viszont a további négy különbség mind nagyobb 2-nél,akkor vagy mindegyik a 4 értéket veszi fel, vagy a 2, 2, 4, 4, 4, 6 értékek lépnek fel valamilyen sorrendben a kiválasztott számok közül a szomszédosak különbségeiként.
Ezzel igazoltuk a feladat állítását, sőt annál többet is. Beláttuk, hogy a 24-nél kisebb páratlan természetes számok közül bárhogy választva ki hetet és azokat nagyság szerint rendezve a szomszédos számok közti hat különbség közül legalább három veszi fel a 2 értéket, vagy legalább három a 4 értéket. Mind a két eset elő is fordulhat. Csak a 2 lép fel háromszor pl. a 2, 2, 2, 4, 4, 8 értékek közt (összegük 22), és ezek lépnek fel az 1, 3, 5, 7, 11, 15, 23 számok közül a szomszédosak különbségeiként, vagy más sorrendben pl. az 1, 9, 11, 13, 15, 19, 23 számok közt. A 2, 2, 4, 4, 4, 4 számok közt (összegük 20) viszont csak a 4 lép fel kettőnél többször. Ennek megfelel pl. a 3, 5, 7, 11, 15, 19, 23 számok, vagy az 1, 3, 7, 11, 13, 17, 21 számok kiválasztása is.
 

Megjegyzések. 1. Ha még a 25 előfordulását is megengedjük a kiválasztandó hét szám közt, akkor a szomszédosak különbségei közt nem föltétlenül szerepel egy érték háromszor, így lehetnek a kérdéses különbségek 2, 2, 4, 4, 6, 6 és könnyen látható, hogy sorrendtől eltekintve csak ezek (minden más esetben vagy a 2, vagy a 4, vagy a 6 legalább háromszor fordul elő köztük). Ez esetben is előfordul azonban az összes különbségek közt legalább egy érték háromszor. Ha ugyanis kétszer egymásután következik 2 távolságra két szám, akkor az első és harmadik közt 4 a különbség (és ez a különbség még két szomszédos számokból álló párban is fellép); ha az egyik 2-es különbség mellett egy 4-es különbség lép fel, akkor fellép egy ,,második szomszéd'' pár közt is a 6-os különbség; végül a 2-esek csak a 2, 6, 2, 6, 4, 4, a 2, 6, 4, 4, 6, 2 és a 4, 4, 6, 2, 6, 2 sorrendekben nem szomszédosak sem egymással, sem 4-es különbséggel. Ekkor azonban az első és harmadik, harmadik és ötödik, ötödik és hetedik szám különbsége egyaránt 8 mind a három esetben.
Beláttuk tehát, hogy a feladat állítása akkor is helyes marad, ha a 26-nál nem nagyobb páratlan természetes számok közül választunk ki hetet.
2. Ezen túl már nem tágíthatjuk a kiválasztható számok körét, mert pl. az 1, 3, 7, 15, 17, 23, 27 számok különbségei közt egyetlen érték sem fordul elő háromszor, amint erről az olvasó könnyen meggyőződhet.
Az első megoldáshoz fűzött megjegyzésben említettük, hogy 3-nál többször egy értéknek sem kell szerepelnie a fellépő különbségek közt, és ha nem hét, hanem csak hat számot választunk ki, akkor az 1, 3, 7, 11, 17, 19 példán látható, hogy már a 20-nál kisebb páratlan természetes számok közül is kiválasztható hat úgy, hogy különbségeik közt egy érték se lépjen fel háromszor.
3. A feladat állítása általánosítható úgy, hogy egyidejűleg növeljük a kiválasztható páratlan számok körét és a kiválasztandó számok számát. Ekkor a II. megoldás gondolatmenetével a következő általánosabb tétel látható be: Legyen k a 2-nél nagyobb egész szám. Ha bárhogy választunk is ki a 2k(k+1)+2-nél kisebb természetes számok közül 2k+1-et, van olyan érték, amelyik az ezek közt fellépő különbségek közt legalább háromszor előfordul.