Cím: Az 1960. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok és megoldásuk: A haladók versenyének feladatai
Szerző(k):  Lőrincz Pál ,  Surányi János 
Füzet: 1960/október, 53 - 56. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

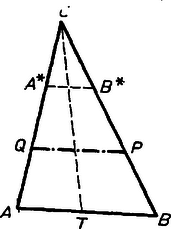
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Adott egy ABC háromszög. Szerkesszük meg a háromszög BC oldalán azt a pontot, melyen át AB-vel párhuzamos egyenest húzva a keletkezett trapéz és kis háromszög kerülete egyenlő!

 
I. megoldás: Gondoljuk a feladatot megoldottnak és legyen a keresett, AB-vel párhuzamos egyenesnek BC-vel, ill. AC-vel alkotott metszéspontja P, ill. Q. A PQ szakasz a kis háromszög és a trapéz kerületének egyaránt része, ezért a kerületek egyenlőségére vonatkozó követelmény így is írható:
PC+CQ=PB+BA+AQ,(1)
és így PC+CQ egyenlő az ABC háromszög kerületének felével.
 
 

Másrészt mivel QP párhuzamos AB-vel, azért a CPQ és CBA háromszögek hasonlók, és így
PC:CQ=BC:CA.(2)

Ezek alapján először k/2=(AB+BC+CA)/2 hosszúságú egyenesszakaszt szerkesztünk, majd ezt BC:CA arányban kettéosztjuk, és így nyerjük a keresett PC, ill. CQ szakaszt.
 
Szerkesztésünk helyessége nyilvánvaló; P mindig a BC szakaszon adódik, mert PC+CQ=k/2 a háromszög-egyenlőtlenség folytán kisebb BC+CA-nál.
 
II. megoldás: Tükrözzük A-t a Q, B-t a P pontra nézve, így nyerjük az A*, B* pontokat. (l)-ből az így létrejött további egyenlő darabokat elhagyva
B*C+CA*=BA.
Másrészt nyilvánvaló, hogy A*B* párhuzamos AB-vel, amiből következik, hogy
B*C:CA*=BC:CA.
Eszerint az AB oldalt a BC és CA oldalak arányában osztva nyerjük a B*C és CA* szakaszokat, a keresett P, Q pont pedig a BB*, AA* szakasz felezőpontja.
 
Megjegyzések: 1. Itt az I. megoldáshoz képest azt nyertük, hogy a felosztandó szakaszt nem kell szerkesztenünk. A felosztás igen egyszerűen adódik az ACB szög CT felezőjével.
2. A feladat általánosítható: előírhatjuk, hogy a kis háromszög és a trapéz kerületei egyenlőség helyett adott λ (λ≠1,λ>0) arányban álljanak:
PC+CQ+QP=λ(PB+BA+AQ+QP),(3)
(ahol λ-t úgy tekintjük adottnak, hogy ismerjük az egységnyi hosszúságú és a λ hosszúságú szakaszt). Előírhatjuk azt is, hogy az (1) két oldalán álló összegek aránya legyen egy adott μ érték:
PC+CQ=μ(PB+BA+AQ).(4)
Ezekkel a feladat így hangzik: Adott az ABC háromszög. Szerkesszük meg a BC oldalon a P, és az AC oldalon a Q pontot úgy, hogy PQ párhuzamos legyen BA-val és teljesüljön (3), ill. (4).
Tekintsük előbb a (4) követelmény esetét. Adjunk (4) mindkét oldalához μ(PC+CQ)-t, így
(1+μ)(PC+CQ)=μ(BC+BA+AC),
másképpen
(PC+CQ):(BC+BA+AC)=μ:(1+μ).(4')
Ennek alapján első lépésül a háromszög kerületéhez és a μ, 1+μ szakaszhoz negyedik arányosként megszerkesztjük PC+CQ-t, majd ezt (2)-nek megfelelően két részre osztjuk.
Megoldás létezésének feltétele, hogy PC+CQ kisebbnek adódjék BC+CA-nál. Ezt (4') csekély átalakításával úgy is mondhatjuk, hogy a μ:1 arány értéke kisebb legyen (BC+CA):AB-nél; egyenlőség esetén a P pont B-be, Q pedig A-ba esik, a trapéz elfajul egyenesszakasszá.
A (3) követelmény esetében a PC=a', QC=b', QP=c', BC=a, AC=b, AB=c egyszerűbb jelölésekkel a fentemlített hasonlóság alapján b'=ba'/a és c'=ca'/a. Ezek alapján (3) így alakítható:
a':a=k:(1+λλk-2c),
amiből a' az előbbi esethez hasonlóan megszerkeszthető.
A megoldhatóság feltétele, hogy a' kisebbnek adódjék a-nál, másképpen, hogy ‐ a legutóbbi aránypárból ‐ a λ:1 arány értéke kisebb legyen k:2c-nél. Egybetűs jelölésekkel a (4) követelmény hasonlóan így alakítható:
a':a=k:1+μμ(k-c).

 
2. feladat. Bizonyítsuk be, hogy bármely hegyesszögű háromszögnek van két olyan szöge, amelyek különbsége kisebb 30∘-nál!
 
I. megoldás: Az állítás egyenlő szárú háromszögre nyilván igaz, hiszen a két egyenlő szög különbsége 0∘. Ezért feltehetjük, hogy a szokásos jelölésekkel
α>β>γ,(1)
és a feladat megszorításánál fogva
α<90∘.(2)
Az állítást indirekt úton bizonyítjuk. Feltesszük, hogy van olyan háromszög, amelyben
α-β≥30∘,(3)
és
β-γ≥30∘,(4)
és megmutatjuk, hogy ilyen háromszög nem lehet hegyesszögű. Valóban, (3) kétszeresét és (4)-et hozzáadva a szögekre érvényes
α+β+γ=180∘(5)
egyenlőséghez, azt kapjuk, hogy
3α≥270∘,azazα≥90∘.
Eszerint hegyesszögű háromszögre (3) és (4) egyidejűen nem teljesülhet, ezért legalább az egyik szögkülönbség kisebb 30∘-nál. Ezt kellett bizonyítanunk.
 
Megjegyzések: 1. Meggondolásunkat egyenlőtlenségekkel való műveletek nélkül is elmondhatjuk. Feltesszük, hogy van olyan pozitív δ és ε szög, hogy
β=α-(30∘+δ)(3')
és
γ=β-(30∘+ε).(4')
Előbb (4')-t, majd (3')-t (5)-be helyettesítve átalakítással az
α=90∘+2δ+ε3
összefüggésre jutunk, ami ellentmond (2)-nek.
2. Több efféle úton járó versenyző szükségtelenül feltette, hogy δ=ε, vagyis hogy α-β=β-γ. Az ilyen megoldások nem teljesek, hiszen csak egy további speciális feltételnek eleget tevő háromszögekkel foglalkoznak; még jobban látszik ez abból, hogy minden ilyen háromszögben β=60∘.
3. Többen ilyenféleképpen kezdték okoskodásukat: ,,legyen α csak egy kevéssel kisebb 90∘-nál, pl. 89∘59'''. Az ilyen feltevés ‐ még ha azt helyes okoskodás követi is ‐ eleve lemond a bizonyítás teljességéről, hiszen figyelmen kívül hagyja mindazokat a hegyesszögű háromszögeket, melyek legnagyobb szöge 90∘ és 89∘59' közé esik. Az idézett feltevés abból a hibás szemléletből ered, mintha létezne a 90∘-nál kisebb szögek között egy legnagyobb szög. Ilyen azonban nincs.
 
II. megoldás: Vizsgáljuk a háromszögnek nagyságra nézve középső szögét, azaz (1) szerint β-t. Ha ez legalább 60∘, akkor α-β<30∘; ha viszont β<60∘, akkor α+β<150∘, és így γ=180∘-(α+β)>30∘, tehát β-γ<30∘. A feladat állítása tehát mindkét esetben teljesül.
 
3. feladat. Bizonyítsuk be, hogy bármely öt egymás után következő egész szám négyzetének összege osztható 5-tel, de 25-tel nem osztható!
 
Megoldás: A szimmetria érdekében jelöljük az öt egymás után következő egész szám közül a középsőt a-val, ekkor a feladat annak igazolása, hogy az
S=(a-2)2+(a-1)2+a2+(a+1)2+(a+2)2=5(a2+2)
szám osztható 5-tel, de 25-tel nem osztható.
a és azért a2+2 is egész és S első tényezője 5, ezért S osztható 5-tel. S akkor és csak akkor lenne 25-tel is osztható, ha a második tényezője, a2+2 is osztható volna 5-tel. Evégett a2+2-nek vagy 0-ra, vagy 5-re kellene végződnie, tehát a2 végződése 8, vagy 3 lenne. Négyzetszám azonban sem 8-ra, sem 3-ra nem végződhet, ezért a2+2 sem végződhet 0, vagy 5-re, tehát 5-tel nem lehet osztható a semmilyen egész értéke mellett sem, és így S nem osztható 25-tel.
 
Megjegyzés: Elkerülhetjük a négyzetszámok lehetséges végződéseire történő hivatkozást, ha megvizsgáljuk az a2+2 kifejezés 5-tel való oszthatóságát minden 5-tel való oszthatóság szempontjából különböző a mellett. Ezek a következők:
a=5b (ahol b egész szám), ekkor a2+2=25b2+2, és ez 5-tel osztva 2-t ad maradékul;
a=5b±1 esetén a2+2=25b2±10b+3, ez 5-tel osztva 3-at ad maradékul;
a=5b±2 esetén a2+2=25b2±20b+6, ez 5-tel osztva 1-et ad maradékul.
Végigvizsgáltunk minden lehetséges esetet, és azt találtuk, hogy a2+2 egyik esetben sem osztható 5-tel.