Kezdőlap


Cím:	Az 1960. évi Arany Dániel matematikai tanulóversenyek I. fordulóján kitűzött feladatok és megoldásuk: A kezdők versenyének feladatai
Szerző(k):	Bakos Tibor , Lukács Ottó , Surányi János
Füzet:	1960/október, 49 - 53. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Bizonyítsuk be, hogy ha két egész szám különbsége $2$ , akkor a két szám köbének különbsége három négyzetszám összegére bontható.

I. megoldás: Próbálgatással könnyen kapjuk a következő felbontásokat:

\begin{matrix} 3^{3} & - 1^{3} = 26 = 1^{2} + 3^{2} + 4^{2} = 0^{2} + 1^{2} + 5^{2}, \\ 4^{3} & - 2^{3} = 56 = 2^{2} + 4^{2} + 6^{2}, \\ 5^{3} & - 3^{3} = 98 = 3^{2} + 5^{2} + 8^{2} = 1^{2} + 4^{2} + 9^{2} = 0^{2} + 7^{2} + 7^{2}, \\ 6^{3} & - 4^{3} = 152 = 4^{2} + 6^{2} + 10^{2} = 2^{2} + 2^{2} + 12^{2}, \\ 2^{3} & - 0^{3} = 8 = 0^{2} + 2^{2} + 2^{2}, \\ 1^{3} - ( & - 1)^{3} = 2 = {(- 1)}^{2} + 1^{2} + 0^{2}, \\ {(- 2)}^{3} - ( & - 4)^{3} = 56 = {(- 4)}^{2} + {(- 2)}^{2} + {(- 6)}^{2} . \end{matrix}

Észrevesszük, hogy mindegyik különbség elsőnek írt felbontásában az első két négyzetszám alapja az a két szám, amelyek köbeinek különbségét éppen vizsgáljuk, a harmadik négyzetszám alapja pedig az előbbi kettőnek az összege. Ezek alapján azt sejtjük, hogy a vizsgálandó számokat

n

és

n + 2

-vel jelölve bármely

n

mellett fennáll

\begin{matrix} {(n + 2)}^{3} - n^{3} = n^{2} + {(n + 2)}^{2} + {(2 n + 2)}^{2} . \end{matrix}

(1)

Sejtésünk bizonyítására a két oldali hatványokat kifejtve mindkét oldalon

6 n^{2} + 12 n + 8

-at kapunk, tehát (1) helyes. Ha

n

és vele

n + 2

egész szám, akkor összegük is az, tehát a jobb oldal mindhárom tagja négyzetszám. Evvel az állítást igazoltuk.

Megjegyzések: 1. Kevesebb konkrét próbálgatást végzünk a következő meggondolásban, és nem lesz szükség bizonyításra. Nyilvánvaló, hogy a köbök

\begin{matrix} {(n + 2)}^{3} - n^{3} = 6 n^{2} + 12 n + 8 \end{matrix}

(2)

különbségében

n

-et változtatva a négyzetszámok alapjai is változnak, függnek

n

-től. Tegyük fel, hogy van olyan felbontás, melyben az alapok

n

-nek elsőfokú függvényei, vagyis ilyen alakúak:

\begin{matrix} a n + b, c n + d, e n + f, \end{matrix}

(3)

ahol

a

b

c

d

e

f

egész számok. Ezek négyzetösszege átrendezéssel

\begin{matrix} (a^{2} + c^{2} + e^{2}) n^{2} + 2 (a b + c d + e f) n + (b^{2} + d^{2} + f^{2}) . \end{matrix}

(4)

Ha találunk olyan

a, b, ..., f

egész számokat, amelyekkel (4) egymás utáni együtthatói egyenlők a (2) jobb oldalán álló együtthatókkal:

\begin{matrix} a^{2} + c^{2} + e^{2} = 6, \end{matrix}

(5)

\begin{matrix} 2 (a b + c d + e f) = 12, \end{matrix}

(6)

\begin{matrix} b^{2} + d^{2} + f^{2} = 8, \end{matrix}

(7)

evvel igazoltuk az állítást, és a talált

a, b, ..., f

számokkal képezett (3) kifejezések minden

n

-re adnak egy alapszám-hármast a kívánt négyzetösszegfelbontáshoz.
(5) és (7) szerint az

a, b, ..., f

együtthatók négyzetei számára csak a

6

-on,

8

-on aluli négyzetszámok jönnek szóba:

0

1

és

4

. Ezek közül vett három tagból a

6

-os,

8

-as összeg

1 + 1 + 4

, ill.

0 + 4 + 4

alakban kiadódik. Ennek alapján vehetjük egyrészt, hogy

a = c = 1

e = 2

, másrészt hogy,

b

d

f

értékei valamely sorrendben a

0

2

2

számok, és e sorrendet cserélgetve megvizsgálhatjuk, hogy teljesül-e (6). Mindjárt a

b = 0

d = f = 2

értékrendszerrel való próba eredményes, ezekkel a (3) kifejezések az (1) jobb oldalán álló alapokat adják.
2. Az (1) jobb oldalán álló alapszámok bármelyike helyett

(- 1)

-szeresét véve ‐ vagyis pl.

c

és

d

előjelének egyidejű cseréjével ‐ csupán látszólag kapnánk újabb felbontást, hiszen így maguk a négyzetszámok ugyanazok maradnak. (Ilyenkor (5) és (7)-ben a négyzetek, és (6)-ban a szorzatok értéke változatlan.) Felvetődik azonban a kérdés: található-e a (3) együtthatói számára adódott számok sorrendjének, valamint pl.

c

és

d

egyikének előjelét megváltoztatva ‐ vagy másképpen ‐ az (1)-től lényegesen különböző felbontás?
Nyilván sem (5)-ben, sem (7)-ben nem lehetséges más megfelelő előállítás. Továbbá, hogy az eddigi

b = 0

d = 2

értékeket felcserélve sem kapunk új felbontást,

f = 0

b = 2

-vel pedig a (6) bal oldalán álló

a b + c d + e f

kifejezés értéke kisebbnek adódik. Mindig az eddigi

6

-nál kisebbnek adódik ez a kifejezés, vagy változatlan marad, ha bármelyik tagjának egyik tényezőjét ellentett jellel próbáljuk venni. Így tehát nem kapunk új felbontást.
Nem jöhet szóba a (3)-beliek helyére elsőnél magasabb fokú kifejezés sem ‐ pl. egy vagy több másodfokú ‐, mert ilyenek négyzetében a legmagasabb fokú tag pozitív, és így összegük nem lehet

0

, amint (2) jobb oldala kívánná.
3. Legutóbbi meggondolásunkat nem teszi feleslegessé az az észrevétel, hogy

4^{3} - 2^{3} = 56

-ra csak a

2^{2} + 4^{2} + 6^{2}

felbontást adtuk, és könnyű belátni, hogy más ilyen felbontás nincs. Gondolni kell ugyanis arra, hogy e felbontás

2

4

6

alapszámait más (3) alakú kifejezések is kiadhatnák

n = 2

-vel.

II. megoldás: Ismert azonosság szerint

\begin{matrix} x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2}) . \end{matrix}

Innen az

x - y = 2

értéket figyelembe véve, alkalmas csoportosítással azonnal adódik, hogy

\begin{matrix} x^{3} - y^{3} = 2 x^{2} + 2 x y + 2 y^{2} = \\ = x^{2} + y^{2} + {(x + y)}^{2}, \end{matrix}

amit bizonyítanunk kellett.

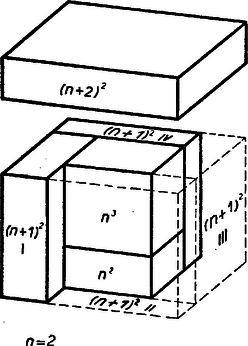
Megjegyzés: Pozitív

n

esetére a bebizonyított azonosságnak geometriai jelentést adhatunk, ha (1)-et a következő alakban írjuk:

\begin{matrix} {(n + 2)}^{3} = n^{3} + n^{2} + {(n + 2)}^{2} + 4 {(n + 1)}^{2} . \end{matrix}

(8)

Tekintsünk minden tagot egy-egy test térfogata mértékszámának. Így a köbök

n + 2

, ill.

n

egységnyi élű kockák, a négyzetek pedig hat olyan egységnyi magasságú, négyzetes oszlop térfogatát jelentik, amelyeknek alapéle rendre

n

n + 2

, ill. négy esetben

n + 1

egység.

Így (8) azt fejezi ki, hogy a nagyobb kocka térfogata egyenlő a további

7

test térfogatának összegével. Ennél többet láthatunk be könnyen: a

7

testből, mindegyiket tömörnek tekintve, hézagtalanul össze is lehet állítani egy a nagyobbal egybevágó kockát. Fektessük le evégett az ,,

n^{2}

-térfogatú'' oszlopot, állítsuk rá az ,,

n^{3}

''-kockát úgy, hogy a 4‐4 oldallapjuk síkjai egybeessenek, így

n

egységnyi alapélű,

n + 1

magasságú

O_{1}

oszlopot kapunk. Állítsuk

O_{1}

köré egy oldallapjukon állva, négyzetlapjukkal

O_{1}

egy-egy oldallapjához zárva a négy

{(n + 1)}^{2}

térfogatú oszlopot úgy, hogy egy-egy oldallapjuk a belső oszlop egy-egy oldallapjának síkjába essék, így

n + 1

egységnyi magas és

n + 2

alapélű

O_{2}

oszlopot kapunk. Végül fektessük rá

O_{2}

-re az

{(n + 2)}^{2}

térfogatú oszlopot úgy, hogy oldallapjaik síkjai egybeessenek.

2. feladat. Határozzuk meg ügyesen a következő számot:

\begin{matrix} \frac{12 346 \cdot 24 689 \cdot 37 033 + 12 347 \cdot 37 034}{12 345^{2}} . \end{matrix}

Megoldás: Vegyük észre, hegy a nevező

1

-gyel, ill.

2

-vel tér el a számlálóbeli szorzatok első tényezőitől, továbbá hogy a két szorzat utolsó tényezői a nevező

3

-szorosánál

2

-vel, ill.

1

-gyel kisebbek, végül, hogy a

24 689

tényező

1

híján

2

-szer akkora, mint a nevező. Ezért egyszerűsítést remélhetünk attól, ha a

12 345

számot átmenetileg

c

-vel jelöljük, evvel minden más előforduló számot a fentiek szerint egyszerűen kifejezünk és igyekszünk az így adódó kifejezést úgy átalakítani, hogy

c

értékének visszahelyettesítése után egyszerűen kiszámítható legyen. Valóban

\begin{matrix} \frac{(c + 1) (2 c - 1) (3 c - 2) + (c + 2) (3 c - 1)}{c^{2}} = \\ = \frac{(6 c^{3} - c^{2} - 5 c + 2) + (3 c^{2} + 5 c - 2)}{c^{2}} = \frac{6 c^{3} + 2 c^{2}}{c^{2}} = \\ = 6 c + 2 = 2 (3 c + 1) = 2 (3 c - 1) + 4, \end{matrix}

ennélfogva a keresett számot az utolsó három alak bármelyikéből könnyen megkaphatjuk; értéke ‐ pl. az utolsó alakból ‐

2 \cdot 37 034 + 4 = 74 072

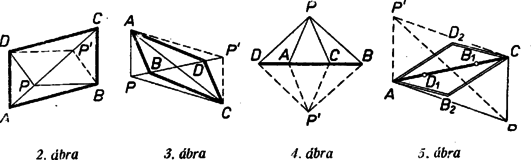
3. feladat. Szerkesszük meg az

A B C D

paralelogrammát, ha ismerjük

A C

átlóját és csúcsainak a sík egy

P

pontjától mért

P A

P B

P C

P D

távolságát.

Megoldás: A

P A C

háromszöget meg tudjuk szerkeszteni, mert ismerjük mind a három oldalát (1. ábra). A

B

és

D

pontok kitűzéséhez ismerjük a

P B D

háromszög

P B

és

P D

oldalát, és további adatot ad az a felismerés, hogy az

A C

és

B D

átlók

F

metszéspontja mindkét átlónak felezőpontja. Így a

P A C

háromszögből kiadódó

P F

szakasz

P B D

-nek is súlyvonala.

1. ábra

Adatainkból a

P B D

háromszög megszerkesztése, mint ismeretes, azon alapszik, hogy a háromszöget

F

-re tükrözve

B

és

D

egymás tükörképei lesznek, és

P

tükörképét

P'

-vel jelölve a

P B P' D

négyszög paralelogramma. Eszerint

P' B = P D

és

P' D = P B

, ennélfogva

B

-t a

P

körül

P B

és

P'

körül

P D

sugárral írt körök metszéspontja adja,

D

pedig a

P B P' D

paralelogramma negyedik csúcsa lesz.
A kapott

A B C D

négyszög megfelel a követelményeknek, mert csúcsai az előírt távolságokra vannak

P

-től, egyik átlója a kívánt

A C

hosszúság, végül a négyszög paralelogramma, mert átlói (

F

-ben) felezik egymást.
Mivel az ábrán

F

-re

A

és

C

, valamint

P

és

P'

tükrös párok, azért

P'

P A C

háromszöget paralelogrammává egészíti ki. Így

P'

-t

F

ismerete nélkül is kitűzhetjük. És mivel

F

-et tovább sem használjuk fel, megszerkesztése mellőzhető. Ezért

F

-et a diszkusszióban nem említjük.
A

P A C

háromszög és vele az

A P C P'

paralelogramma egyértelműen megszerkeszthető, ha az adott

A C

P A

és

P C

szakaszok közül bármelyik kettőnek összege nagyobb a harmadiknál. A

P B P' D

paralelogramma megszerkeszthető, ha a létrejött

P P'

és adott

P B

P D

szakaszok közül bármelyik kettő összege nagyobb, mint a harmadik, éspedig 2 megoldást kapunk, ha

P D \neq P B

, ha pedig

P D = P B

, akkor egyet. Eszerint

A B C D

-re is a megoldások száma 2. Mert bár a

P B P' D

-re adódó két megoldás egybevágó ‐ egymásnak

P P'

-re tükörképei ‐ a velük adódó

A B C D

paralelogrammák mégsem egybevágók, mert

P P'

A P C P'

paralelogrammának általában nem tengelye. Ha azonban

P A = P C

, és így

P A P' C

rombusz, akkor a (

P B \neq P D

mellett) adódó két

A B C D

paralelogramma egymásnak

P P'

-re tükörképe.

Eljárásunk akkor is használható, ha vagy az első három, vagy pedig az utóbbi három egyenlőtlenség közül az egyikben egyenlőség teljesül, mert ilyenkor

P

és

P'

A C

egyenesre, ill.

B

és

D

P P'

egyenesre esnek, de a 4 pont egy egyenesre esése csak egyszer fordul elő (2-3. ábra). Ha mindkét egyenlőtlenséghármas közül egyben-egyben egyenlőség lép fel, akkor mind a hat pont egy egyenesre esik, a paralelogramma elfajul egyenesszakasszá.
Kivétel a legutóbbi megjegyzésünk alól a

P A = P C = A C / 2

eset, amikor

C

A

pont

P

-re vonatkozó tükörképének adódik, és így

P'

egybeesik

P

-vel,

P P' = 0

. Ilyenkor ugyanis a

P B P' D

paralelogramma is elfajult és vagy egyáltalán nem szerkeszthető még elfajultan sem, ‐ ha ti.

P D \neq P B

‐ vagy végtelen sokféleképpen szerkeszthető ‐ ha

P D = P B

. Ilyenkor tulajdonképpen a két átlójából kellene megszerkeszteni a paralelogrammát.
Megjegyezzük még, hogy az

A B C D

paralelogramma akkor is adódhat elfajultnak, ha sem az

A P C P'

, sem a

P B P' D

paralelogramma nem elfajult, pl. ha

P A = P C (> A C / 2)

és

P B = P D

(4. ábra); sőt az egyik megoldás

P A \neq P C

és

P B \neq P D

esetén is lehet elfajult (5. ábra).

Megjegyzés: A feladat könnyen visszavezethető egy jól ismert négyszögszerkesztési feladatra. Toljuk el a

P C D

háromszöget úgy, hogy a

C D

oldal a vele párhuzamos és egyenlő

A B

oldalra kerüljön. Az így keletkező

A P B P'

négyszögben adottak az oldalak. Hogy a paralelogramma

A C

átlóját is kapcsolatba hozzuk ezzel a négyszöggel, figyeljük meg, hogy a

B C P P'

négyszög paralelogramma, s így

B P

és

C P'

átlóinak

E

metszéspontja mindkét átlót felezi. Így az

A P B P'

négyszög két nem szomszédos oldalának,

A P'

-nek és

B P

-nek a felezőpontjait összekötő

E F

szakasz egyben az

A C P'

háromszögnek középvonala, tehát

A C

felével egyenlő, s így adottnak tekinthető. A versenyfeladat tehát ekvivalens a következő ismert feladattal:^{$^{*}$} szerkesszünk négyszöget, ha adott az oldalak hossza és két nem szomszédos oldal felezőpontjának távolsága. A keletkező négyszög adódhat konkávnak vagy hurkoltnak is. (Ezért is kerültük el a ,,szemközti oldalak'' megjelölést.)

^{$^{*}$}Lásd pl. az I. o. gimn. tankönyvben (1959. évi kiadás) a 242. o. 18. feladatában.