Cím: Az 1960. évi Országos Középiskolai Matematikai Tanulmányi Verseny II. fordulóján kitűzött feladatok megoldása
Szerző(k):  Bakos Tibor ,  Surányi János 
Füzet: 1960/november, 97 - 104. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Állapítsuk meg az

y=2x2+6x+6x2+4x+5
függvény maximumát és minimumát !
 

I. megoldás: Fejezzük ki az adott kapcsolatból x-et y-nal. Így megadhatjuk, mely y-okhoz lehet x-et kiszámítani, más szóval, hogy mely y számokhoz van olyan x érték, amelyre függvényünk az y értéket veszi fel, vagyis mi függvényünk értékkészlete. Ebből már kiválaszthatjuk a keresett maximumot, ill. minimumot ‐ hacsak az értékkészletben van legnagyobb, ill. legkisebb szám.
A nevező sehol sem 0, mert x2+4x+5=(x+2)2+1≥1, ezért az átszorzással és rendezéssel adódó
(y-2)x2+(4y-6)x+(5y-6)=0
kapcsolat ekvivalens az eredetivel. Innen
x=-4y+6±-4y2+16y-122(y-2),(1)
hacsak y≠2, és x=-2, ha y=2.
x a gyökképletből akkor és csak akkor adódik valósnak, ha a diszkrimináns nem negatív, vagyis ha ‐ a másodfokú kifejezést mindjárt szorzattá alakítva ‐
-4(y-1)(y-3)≥0.
Ez pedig nyilván akkor és csak akkor teljesül, ha
1≤y≤3.

Ez a kettős egyenlőtlenség írja le függvényünk teljes értékkészletét, mert ennek a külön úton nyert fenti y=2 szám is eleget tesz. Eszerint függvényünknek van maximuma is, minimuma is, éspedig az
ymax=3,ill.ymin=1
érték. Ezeket a függvény (1) szerint az
xmax=-3,ill.xmin=-1
helyen veszi fel.
 

Megjegyzés. Néhány dolgozat a helyes eredményre a következő téves meggondolással jutott el: ,,maximum és minimum azok az értékek, amelyeket a függvény csak egyszer vesz fel, ezek azok, ahol a diszkrimináns 0.'' Eszerint minden elsőfokú függvény számára minden érték maximum volna és egyben minimum is; másrészt az y=1 érték nem volna maximuma az y=sinx függvénynek, úgyszintén y=-1 sem volna ennek minimuma, mert mindegyik értéket végtelen sokszor veszi fel. Azt mutatja ez, hogy a szélső értékek fogalma egyedül a másodfokú függvényre alapult.
 

II. megoldás. Osztással és a nevezőben teljes négyzetté való kiegészítéssel az adott kifejezés így alakítható:
y=2-2x+4x2+4x+5=2-2(x+2)(x+2)2+1,
majd x+2 helyére új z változót írva
y=2-2zz2+1=2-2y1,aholy1=zz2+1.(2)

Eszerint y-nak ott van maximuma, ahol az y1 függvény minimális értéket vesz fel, és ott van minimuma, ahol y1 maximális. y1 lehet pozitív, negatív és 0, mert ugyanolyan jelű, mint a z számláló, hiszen nevezője pozitív, z=0 mellett pedig y1=0; ezért y1 maximuma csak pozitív, minimuma csak negatív érték lehet. Elég y1-et pozitív z-k mellett vizsgálni, mert z és -z mellett felvett értékei csak előjelben különböznek, tehát az így meghatározandó maximum értékének, és helyének (-1)-szerese megadja a minimum értékét és helyét.
További átalakítással
y1=zz2+1=1z+1z=1y2,azazy2=z+1z,
így y1 maximuma egyenlő az y2 függvény minimumával. Vegyük észre, hogy pozitív z mellett az y2 összeg két tagjának mértani közepe 1, állandó. Ismeretes másrészt, hogy pozitív számok számtani közepe sohasem kisebb mértani közepüknél, és akkor egyenlő vele, ha a számok egyenlők. Eszerint y2 felének minimuma 1, így y2,min=2, és ez akkor adódik, ha z az a pozitív szám, amelyre z=1/z, vagyis z=1.
Most már y1 maximuma 1/2, és a fentiek szerint minimuma a z=-1 helyen y1,min=-1/2; végül (2) szerint y minimuma 1, maximuma 3, és e szélső értékeket x=z-2 figyelembevételével az x=-1, ill. x=-3 helyen veszi fel.
 

III. megoldás: Alakíthatjuk y-t a következők szerint is:
y=1+x2+2x+1x2+4x+5=1+(x+1)2(x+2)2+1,y=3-x2+6x+9x2+4x+5=3-(x+3)2(x+2)2+1.


Az első alak második tagja sohasem negatív, mert számlálója teljes négyzet és nevezője pozitív. Eszerint y minimumát x+1=0-nál, vagyis az x=-1 helyen veszi fel; itt a második tag 0, és y értéke 1. Hasonlóan a második alak kivonandója akkor legkisebb, ha x+3=0, azaz x=-3, és itt értéke 0, tehát y maximuma 3.
 

2. feladat. Adott egy kör és a kör belsejében fekvő P pont. Tekintsük a kör egy félkörnél kisebb AB ívét és jelöljük ennek felezőpontját F-fel. Bizonyítandó, hogy ha
PA<PB(1)
akkor
APF∢>FPB∢.(2)

I. megoldás: A feltevések folytán P az F ponthoz tartozó FG átmérővel kettévágott k kör azon félkörének belsejében van, amelynek ívén A fekszik.
a) Tulajdonképpen csak az AFG szögtartományban fekvő P pontokra kell bizonyítást adnunk, mert az FA húrral lemetszett kisebb körszeletben levő P pontokra az állítás magától értetődő, hiszen ilyenkor A és B az FP egyenes ugyanazon partján vannak, és ezért az FPB szög része az APF szögnek (1. ábra).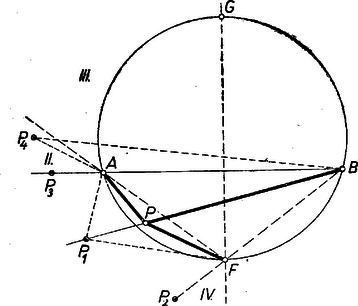
 
 
1. ábra
 

Másképpen: ilyen esetekben a PB félegyenes benne van az APF szögtartományban.
b) Ugyanez áll akkor is, ha P az FA húron van, mert ilyenkor az APF szög bármelyik irányú forgással 180∘, az FPB szög pedig kisebb.
c) Ha P az AFG szögtartományban van, akkor FP szétválasztja A-t és B-t. (2. áb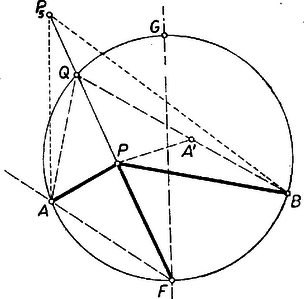ra).
 
 
2. ábra
 

Tükrözzük FP-re az APF szöget, legyen az A pont tükörképe A'. Ekkor elegendő azt igazolnunk, hogy az FPB szög része az FPA-val egyenlő FPA' szögnek. ‐ Messe az FP egyenes k-t másodszor Q-ban. Így egyrészt az FQA és FQB szögek egyenlők, mert k-nak a száraik közti FA, FB ívei egyenlők, másrészt a tükrözés folytán az FQA és FQA' szögek egyenlők, és ezért A' és QB egyenesen van, továbbá QA'=QA<QB, tehát A' a QB húr belső pontja. Így pedig a PB félegyenes valóban az A'PF szögtartományban van.
A fentiekben az állítást P minden lehetséges helyzetére igazoltuk.
 

Megjegyzések. 1. Nem használtuk fel, hogy az F-fel felezett AB ív kisebb félkörnél, ezért az állítás bármekkora AB ívre érvényes.
2. A bizonyítás a) részében nem használtuk fel, hogy P a k-n belül van, így meggondolásunk az ABF szögtartomány k-n és rajta kívül fekvő I. része minden pontjára érvényes (az 1. ábrán P1), úgyszintén a BF szakasz F-en túli meghosszabbításának P2 pontjaira is, mert így a P2B és P2F félegyenesek egybeesnek, szögük 0. Az I. síkrész másik határoló félegyenesén, a BA szakasz A-n túli meghosszabbításán levő P3 pontokra viszont a két kérdéses szög azonos.
Kézenfekvő most már legalább vázlatosan áttekinteni a kérdéses szögek nagyságviszonyát minden az (1)-et teljesítő P pontra. Ha P kilép I-ből BA-nak A-n túli meghosszabbításán át, de nem lépi át FA-t (II. síkrész, P4), akkor a PB félegyenes kilép az APF szögtartományból, APF része BPF-nek, (2) iránya ellentétesre fordul. Ugyanez adódik a III. síkrészben, vagyis ha P az AFG szögtartománynak k-n kívüli pontja (a 2. ábrán P5), mert ilyenkor a c) alatti Q pont F és P5 közé esik, és így 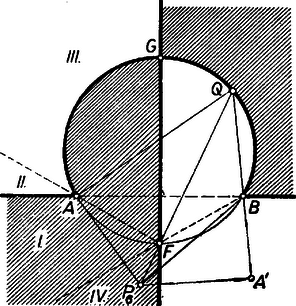A'P5F∢<BP5F∢.
 
 
3. ábra
 

Végül a IV. síkrészben választott P6-tal Q a GB íven adódik (3. ábra), ezért QA'>QB, így AP6F∢=A'P6F∢>BP6F∢, itt tehát érvényes (2). ‐ Most már a PA>PB követelmény mellett a megfelelő síkrészek határvonalait FG-re tükrözéssel kapjuk, így a 3. ábra csíkozott részein a kérdéses szögek közül APF nagyobb, a világosakon FPB nagyobb, a határvonalakon pedig a két szög ‐ amint az könnyen belátható ‐ egyenlő. (Mezei Ferenc ,,térképvázlata'').
A további megoldásokban csak a fenti c) esettel foglalkozunk, ezt 3 alesetre bontjuk fel aszerint, hogy P az AB-nek F-fel ellentétes, ill. megegyező partján van ‐ vagyis az utóbbi alesetben az ABF háromszögben ‐ vagy pedig magán az AB húron. ‐ Mindkét további megoldás Muszély György megoldásainak egyszerűsítése.
 
 
4. ábra
 

II. megoldás: c1) Ha P az AB-nek F-fel ellentétes oldalán van (4. ábra), akkor a kérdéses APF és FPB szögek a kisebb APB szögnek részei. Az A, B, P pontokon átmenő k1 kör P-t nem tartalmazó, vagyis k-n kívül levő AB ívének F1 felezőpontja az AB egyenesnek F-fel egyező oldalára, vagyis GF-nek F-en túl való meghosszabbítására esik. Így F1 az APF szögtartományban van, F pedig az F1PB szögtartományban. Ámde PF1 felezi a kisebb APB szöget, ennélfogva az APF szög F1PF szöggel nagyobb, az FPB szög pedig ugyanennyivel kisebb az APB szög felénél, ez megfelel az állításnak.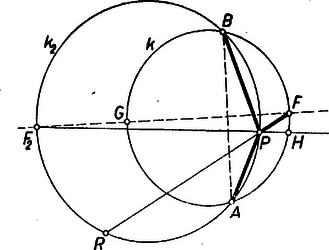
 
 
5. ábra
 

c2) Ha P az AB-nek F-fel egyező oldalán van (5. ábra), akkor az A, B, P pontokon átmenő k2 kör P-t nem tartalmazó, vagyis k-n kívül levő AB ívének F2 felezőpontja az AB egyenesnek F-fel ellentétes oldalára, FG-nek G-n túl való meghosszabbítására esik. A kérdéses APF és FPB szögek egyenes szögnél nagyobb összegét ebben az alesetben F2P-nek P-n túl való PH meghosszabbítása felezi. A PH félegyenes FG-nek A-t tartalmazó oldalán van, ezért az APF szöget osztja részekre. Így az APF szög nagyobb, FPB pedig kisebb az APH=HPB szögnél. Ezt kellett bizonyítanunk.
c3) Végül ha P az AB szakaszon van, akkor (2) fennáll, mert APF tompaszög, FPB pedig hegyesszög.
 

Megjegyzések. 1. A c2) aleset meggondolása nem alkalmazható az FA húrral lemetszett körszeletben felvett P-re, mert ilyen esetben a 180∘-nál nagyobb APF szöget hasonlítanók az FPB szöghöz.
2. Lényegében a fenti meggondolást mondjuk el másképpen annak az R pontnak a helyzetét tekintetbe véve, ahol a PF egyenes a k1, ill. k2 kört másodszor metszi.
A c1) alesetben (4. ábra) F a k1-re nézve belső pont, ezért R egyrészt a PF szakasz F-en túl való meghosszabbításán van, FG-nek P-vel ellentétes, vagyis B-vel egyező oldalán. Másrészt R a P-t nem tartalmazó AB ívnek pontja. Ezek szerint R a (rövidebb) BF1 íven van. Így k1-nek AF1R íve hosszabb a BR ívnél, tehát APR∢>RPB∢, vagyis APF∢>FPB∢.
A c2) alesetben (5. ábra) F a k2-re nézve külső pont, ezért R egyrészt az FP szakasz P-n túli meghosszabbításán van, FG-nek P-vel egyező, B-vel ellentétes oldalán, másrészt az AF2B íven. Így R a (rövidebb) AF2 ívnek pontja, AR^< <RB^, APR∢<RPB∢, ezért 180∘-APR∢>180∘-RPB∢, azaz APF∢>FPB∢.
 

III. megoldás: A feladat állítása akkor és csak akkor igaz, ha az APF háromszög A és F-nél levő (belső) szögeinek összege kisebb, mint a BPF háromszög B és F-nél levő (belső) szögeinek összege. Ezt fogjuk bizonyítani.
Legyen P tükörképe FG-re P', így az APP'B négyszög konvex trapéz.
A c1) alesetben P' az FBP szögtartományban van (6. ábra).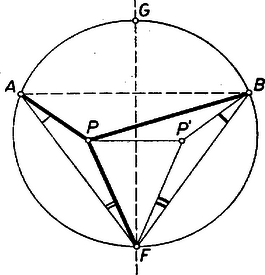
 
 
6. ábra
 

Ugyanis P és P' az ABP háromszög belsejében vannak, tehát P'BA∢<FBA∢, másrészt az ABP háromszögből (1) alapján PBA∢<PAB∢=P'BA∢. Ennélfogva
 

PAF∢=P'BF∢<PBF∢.(3)
Másrészt P' a BFG szögtartományban van, amely része BFP-nek, ezért
PFA∢=P'FB∢<PFB∢.(4)
Most már (3) és (4) két-két szélső tagjának összeadásával a kívánt egyenlőtlenség adódik.
 
 
7. ábra
 

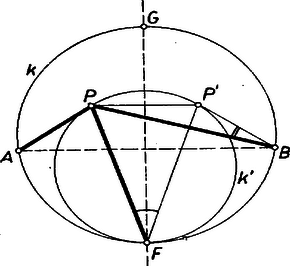Ha pedig AB elválasztja P-t és F-et (7. ábra), akkor egyrészt
PFB∢-PFA∢=PFB∢-P'FB∢=PFP'∢,(5)
ez pedig PP' látószöge F-ből; másrészt
PAF∢-PBF∢=P'BF∢-PBF∢=PBP'∢,(6)
ez pedig PP' látószöge B-ből; ekkor B ugyanazon oldalán fekszik PP'-nek, mint F. ‐ Mármost a PP'F háromszög köré írt k' kör érinti k-t F-ben, minden más pontja k belsejében van, így B a k'-re nézve külső pont. Ezért PP'-nek B-ből vett látószöge kisebb az F-ből vett látószögénél, azaz (5) és (6) alapján
PAF∢-PBF∢<PFB∢-PFA∢.
Innen pedig átrendezéssel
PAF∢+PFA∢<PBF∢+PFB∢,
amit bizonyítani akartunk.
 

3. feladat: Legyen az ABCD konvex négyszög AB és CD oldalának felezőpontja E és F, az AF és DE metszéspontja G, a BF és CE metszéspontja H. Bizonyítandó, hogy az AGD és BHC háromszögek területének összege egyenlő az EHFG négyszög területével.
 

I. megoldás: Húzzuk meg a négyszög AC és BD átlóit. Az AF és CE szakasz az ACD, ill. ABC háromszögben súlyvonal, tehát a háromszöget két egyenlő területű háromszögre osztja (8. ábra):
 
 
8. ábra

ADF=ACF,BCE=ACE(1)
(az idomok területét ugyanúgy jelöljük, mint magukat az idomokat). Ezekből összeadással
ADF+BCE=AECF,(2)
mert az ABCD négyszög konvexsége folytán D és B az AC-nek ellentétes partján feküsznek, és ezért ugyanez áll F és E-re is. Figyelembe véve a DE és BF egyenesekkel való felbontást is, (2)-t így írhatjuk:
ADG+DGF+BCH+BHE=AEG+CFH+EHFG(3)
(mindkét oldalon az ABCD négyszög területének fele áll).
Hasonlóan a DE és BF súlyvonalakkal két-két egyenlő részre osztott ABD és BCD háromszögekből
ADE+BCF=EBFD,(4)
amit részletesebben így írhatunk:
ADG+AEG+BCH+CFH=BHE+DGF+EHFG.(5)
Már most (3) és (5) összegéből a két oldalon fellépő egyenlő tagok elhagyásával és 2-vel való osztással a bizonyítandó egyenlőséget kapjuk:
ADG+BCH=EHFG.

II. megoldás: Ismeretes, hogy a trapézt átlói négy olyan háromszögre bontják, melyek közül a szárakra támaszkodók egyenlő területűek. Ezt a tételt fogjuk háromszor felhasználni. Feltehetjük, hogy D és C közül D van távolabb AB-től. Húzzunk D-n és C-n át AB-vel párhuzamost és jelöljük ezeknek AF meghosszabbításával, ill. BF-fel való metszéspontját D', ill. C'-vel (9. ábra), továbbá ED' és FC' metszéspontját 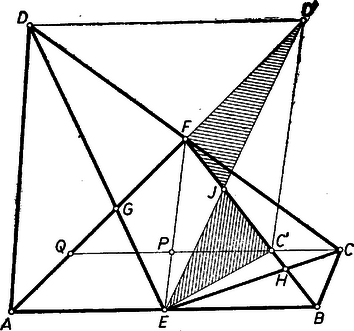J-vel.
 
 
9. ábra
 

AED'D és EBCC' trapézok, így
AGD=EGD'
és
BCH=EHC'.

Az EGD' és EHC' háromszögek együttesen nem takarják le az EHFG négyszöget, kinyúlik az FD'J, nincs lefedve az EC'J háromszög. Ha sikerül igazolnunk, hogy ezek egyenlő területűek, akkor a feladat tételét bebizonyítottuk. Ehhez viszont elegendő megmutatni, hogy C'D' párhuzamos EF-fel, mert ekkor az EC'D'F négyszög trapéz voltából következik állításunk.
Jelöljük CC'-nek EF és AF-fel való metszéspontját P, ill. Q-val. Így EF az AB szakasszal együtt a vele párhuzamos QC' szakaszt is felezi. Másrészt a QCF és D'DF háromszögek egybevágóságából következik, hogy QF=FD'. Tehát P, ill. F a QC'D' háromszög QC', ill. QD' oldalának felezőpontja, és így valóban PF párhuzamos C'D'-vel.
Ha D és C egyenlő távolságra esnek AB-től, akkor D' és C' egybeesnek F-fel, és így az EGD' és EHC' háromszögek együtt pontosan lefedik az EHFG négyszöget.
 

III. megoldás: Azt mutatjuk meg, hogy
AED+EBC=ABF,
illetőleg e területeket 2, 2, ill. 3 idom területének összegeként felírva
AEG+ADG+EBH+BCH=AEG+EBH+EHFG.
Innen ugyanis a két oldal egyenlő tagjainak elhagyásával a bizonyítandó tételt kapjuk.
Valóban, D, F, C-nek AB-n levő vetületét rendre D', F', C'-vel jelölve (8. ábra) a CDD'C' idom trapéz, és benne FF' a középvonal, tehát
DD'2+CC'2=FF'.
Innen pedig mindkét oldalt AE-vel szorozva, majd az AE=EB=AB/2 egyenlőségeket figyelembe véve
12AE⋅DD'+12EB⋅CC'=12AB⋅FF'
adódik, ami állításunkat igazolja.
 

Megjegyzések. 1. A feladat állítása általánosítható: a kimondott területegyenlőség akkor is fennáll, ha E és F az AB, ill. CD oldalt (nem felezi, hanem) ugyanolyan q arányban osztja két-két részre: AE:EB=q, azaz AE=q⋅EB, és ugyanígy CF=q⋅FD (10. ábra, itt 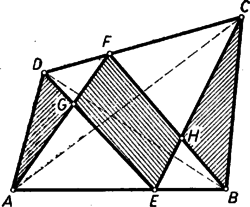q=2).
 
 
10. ábra
 

Az állítás mindhárom fenti megoldás gondolatmenetével igazolható; alább az I. megoldás módosításával bizonyítjuk. Az ott szereplő (1)‐(3) egyenlőségek jobb oldala most a bal oldal q-szorosával lesz egyenlő, (4) és (5) bal oldala viszont a jobb oldal q-szorosával. Így a (3) és (5)-ből keletkezett egyenlőségek összegében 2 helyett (1+q)-val osztva kapjuk az általánosítás állítását. Ez az általánosítás Bollobás Béla dolgozatában szerepel.
2. Könnyű belátni, hogy a nem konvex (vagyis az egy 180∘-nál nagyobb belső szöggel bíró, valamint a hurkolt) négyszögekre az állítás nem igaz.