Kezdőlap


Cím:	Az 1960. évi Országos Középiskolai Matematikai Tanulmányi Verseny I. fordulóján kitűzött feladatok és megoldásuk
Szerző(k):	Bakos Tibor , Lukács Ottó , Scharnitzky Viktor , Surányi János
Füzet:	1960/szeptember, 8 - 16. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat: Hány olyan legfeljebb hatjegyű természetes szám van, amelyben előfordul az 1-es számjegy ?
Előzetes megjegyzés. Számos versenyző azt határozta meg, hány az 1-es számjegyet tartalmazó szám ¹, van külön-külön az egy-, a két-, $...$ , a hatjegyű számok között, és a feladat kérdésére a választ e hat szám összegével adta meg. Ehhez hasonló, de egyszerűbb megoldás a következő.

I. megoldás: Legfeljebb hatjegyűek azok a számok, amelyek leírásához egy, vagy két, vagy

...

, vagy hat számjegy szükséges, más szóval hat számjegy elegendő. Mindezek pontosan hat jeggyel is írhatók, ha a 0 jegyet a többi jegyektől meg nem különböztetve kezdő számjegyként is megengedjük, és minden legfeljebb öt jeggyel írt szám elé annyi 0-t gondolunk írva, hogy jegyeinek száma hat legyen.
Jelöljük az 1-es jegyet tartalmazó legfeljebb

n

-jegyű számok számát

F_{n}

-nel. Így nyilván

F_{1} = 1

, mert az egyjegyű számok közül egy felel meg: az 1, és feladatunk

F_{6}

megállapítása. Tegyük fel, hogy

F_{n}

-et már ismerjük; ekkor

F_{n + 1}

-et a következő meggondolással kaphatjuk meg. Csoportosítsuk az 1-es jegyet tartalmazó legfeljebb

n + 1

jegyű számokat kezdő jegyük szerint. Az 1-essel kezdődők száma

10^{n}

, mert bennük a további

n

helyre tetszés szerint írhatunk jegyeket, mindegyikre a 10-féle jegy mindegyikét, egymástól függetlenül. ² A

0, 2, 3, 4, ...

9

-essel kezdődő

n + 1

jegyűek száma pedig minden csoportban

F_{n}

, hiszen ezeknek a hátralevő

n

jegyű részükben kell 1-est tartalmazniuk. Ezzel valamennyi megfelelő

n + 1

-jegyű számot figyelembe vettük, mindegyiket pontosan egyszer, tehát

\begin{matrix} F_{n + 1} = 10^{n} + 9 \cdot F_{n} . \end{matrix}

Ezzel ún. rekurzív³ képletet kaptunk

F_{n}

kiszámítására. Így

F_{2} = 10 + 9 \cdot F_{1} = 19

F_{3} = 100 + 9 \cdot 19 = 271

F_{4} = 1 000 + 9 \cdot 271 = 3 439

F_{5} = 10 000 + 9 \cdot 3 439 = 40 951

, végül

F_{6} = 100 000 + 9 \cdot 40 951 = 468 559

. ‐ Ezzel a kérdésre a választ megadtuk.

II. megoldás: Csoportosítsuk a szóban forgó számokat aszerint, hogy a legértékesebb helyen álló, más szóval balról első 1-es jegyük rendre az egyes, a tízes, a százas,

...

, a százezres helyen áll. Így hat csoport jön létre és minden számunk pontosan egy csoportba jut. Az előállításban az említett 1-es helyének kivételével mind az öt további helyet úgy kell betöltenünk, hogy az említett 1-es után bármely jegy állhat, előtte pedig bármely 1-től különböző jegy.
Az első csoport számainak az egyes értékű, vagyis balról az utolsó jegye 1-es, több 1-est nem tartalmaznak. Bennük a tízes értékű helyre az 1-estől különböző 9 jegy mindegyikét figyelembe kell vennünk. Bármelyiket véve tízesnek a százas értékű jegy ismét 9-féleképpen töltendő be, így a tízes és százas értékű helyeken

9 \cdot 9

-féle betöltés lehetséges. Ugyanígy a további három hely is 9-féleképpen tölthető be, tehát e csoport

9^{5}

számot tartalmaz.
A második csoportba tartozó számok tízes értékű jegye 1, a mögötte álló egyes értékű helyre mind a 10 jegyet írhatjuk, az előtte álló négy jegyet pedig ismét 9-féleképpen választhatjuk meg, így ebben a csoportban

9^{4} \cdot 10

számot kapunk. ‐ Tovább haladva csoportról csoportra eggyel-eggyel több hely tölthető be 9 helyett 10-féleképpen, így az 1-est tartalmazó számok száma a hat csoportból összesen:

\begin{matrix} N = 9^{5} + 9^{4} \cdot 10 + 9^{3} \cdot 10^{2} + 9^{2} \cdot 10^{3} + 9 \cdot 10^{4} + 10^{5} . \end{matrix}

Vegyük észre, hogy e hat tagú összeg tagjai mértani sorozatot alkotnak

10 / 9

hányadossal, így az összegképlettel

N = 468 559

III. megoldás: Kombinatorikai ismeretekre és a binomiális tételre támaszkodva a kérdéses számok számát az előzőkhöz hasonlóan a bennük fellépő 1-esek száma szerint csoportosított előállításuk alapján is megkaphatjuk, a számokat itt is hatjegyűre kiegészített alakjukban állítva elő. Az egyetlen 1-est tartalmazó számok 1-esét a 6 hely mindegyikén kell figyelembe vennünk, a többi 5 helyen pedig a további 9 jegyet minden lehetséges módon, tehát az ilyen számok száma

6 \cdot 9^{5}

. A pontosan két, három,

...

, hat 1-est tartalmazó számok 1-eseinek helyét rendre

\begin{matrix} (\binom{6}{2}), (\binom{6}{3}), (\binom{6}{4}), (\binom{6}{5}), (\binom{6}{6}) = 1 \end{matrix}

féleképpen választhatjuk meg és minden egyes megválasztás után a többi

4, 3, 2, 1

helyet

9^{4}, 9^{3}, 9^{2},9

-féleképpen tölthetjük be, ill. az utolsó esetben készen is vagyunk, nincs további betöltendő hely. Ezek alapján a keresett szám

\begin{matrix} N = 6 \cdot 9^{5} + (\binom{6}{2}) \cdot 9^{4} + (\binom{6}{3}) \cdot 9^{3} + (\binom{6}{4}) \cdot 9^{2} + (\binom{6}{5}) \cdot 9 + 1. \end{matrix}

Vegyük észre, hogy

N

ezen kifejezéséhez első tagként

9^{6}

-ot adva al

{(9 + 1)}^{6}

hatvány kifejtését kapjuk. Ennek alapján

\begin{matrix} N = {(9 + 1)}^{6} - 9^{6} = 10^{6} - 9^{6} = 1 000 000 - 531 441 = 468 559. \end{matrix}

IV. megoldás: A legutóbbi eredményhez egyszerűbben így juthatunk el. Tekintsük valamennyi hatjegyű és hatjegyűen írható számot, beleértve 0-t is a

000 000

alakban, ezek száma

999 999 + 1

, másképpen

10^{6}

, mert mind a hat helyre mind a 10 jegyet egymástól függetlenül sorra vesszük. A követelménynek megfelelő számokhoz úgy jutunk, ha elhagyjuk az 1-es jegyet nem tartalmazó számokat, más szóval mindazokat, amelyekben a 6 hely mindegyikén 1-estől különböző jegy áll. Ezek száma

9^{6}

, tehát

N = 10^{6} - 9^{6}

. (Eközben a 0-t is elhagytuk.)

Megjegyzések: 1. A II. megoldásban kapott összeget

10 - 9

alakban 1-gyel szorozva a III. megoldásban kapott

10^{6} - 9^{6}

alakra hozhatjuk.
2. A IV. megoldásban azt használtuk fel, hogy valamennyi legfeljebb hatjegyű természetes számnak összessége, ill. az 1-es nem tartalmazása miatt elhagyandó számok összessége ‐ a 0-t mindkét összességbe beszámítva ‐ azonos a 10-, ill. 9-féle számjegy ismétléses 6-odosztályú variációival.
3. Általánosítások: a) Egyik megoldásban sem használtuk ki, hogy a kitüntetett számjegy éppen az 1-es. Eszerint azoknak a legfeljebb hatjegyű természetes számoknak a száma, amelyekben egy adott tetszőleges (0-tól különböző) jegy előfordul:

468 559

.
b) Mindegyik megoldás gondolatmenete akkor is alkalmazható, ha az olyan legfeljebb

n

-jegyű természetes számok számát keressük, amelyekben egy megadott (0-tól különböző) számjegy előfordul. Ezek száma (pl. a IV. megoldásból)

10^{n} - 9^{n}

.
c) Ugyanezt a kérdést egy tetszőleges

k

alapú számrendszerben vizsgálva ‐ ahol

k

az 1-nél nagyobb természetes szám, és a figyelembe vett számjegy nem a 0, ‐ a követelménynek eleget tevő számok száma

\begin{matrix} k^{n} - {(k - 1)}^{n} . \end{matrix}

2. feladat:

a

b

c

olyan számok, melyekre

4 a c - b^{2}

nem-negatív és ,,

a

'' pozitív. Bizonyítandó, hogy

\begin{matrix} a + c - \sqrt[]{{(a - c)}^{2} + b^{2}} \leq \frac{4 a c - b^{2}}{2 a} . \end{matrix}

(1)

Mikor áll fenn egyenlőség ?

I. megoldás: Igyekezzünk az (1) egyenlőtlenséget olyan alakra hozni, melynek helyessége már nyilvánvaló.
Szorozzuk meg (1)-et a feltevés szerint pozitív

2 a

számmal, elegendő az így nyert

\begin{matrix} 2 a^{2} + 2 a c - 2 a \sqrt[]{{(a - c)}^{2} + b^{2}} \leq 4 a c - b^{2} \end{matrix}

egyenlőtlenséget igazolni, vagy ehelyett is az átrendezéssel keletkezett

\begin{matrix} 2 a^{2} - 2 a c + b^{2} \leq 2 a \sqrt[]{{(a - c)}^{2} + b^{2}} \end{matrix}

(2)

egyenlőtlenséget.
a) Ha itt a bal oldal negatív, azaz

2 a^{2} - 2 a c + b^{2} < 0

, akkor az egyenlőtlenség teljesül, mert a jobb oldal a négyzetgyök egyértelmű értelmezése, valamint a feltevés folytán nem lehet negatív. Mivel eddig csak megfordítható átalakításokat végeztünk, ebben az esetben a kiindulási egyenlőtlenség is helyes, mégpedig az egyenlőtlenség jele áll fenn.
b) Ha pedig a bal oldal nem-negatív, akkor elég megmutatni, hogy a bal oldal négyzete nem nagyobb a jobb oldal négyzeténél:

\begin{matrix} {(2 a^{2} - 2 a c + b^{2})}^{2} \leq 4 a^{2} {(a - c)}^{2} + 4 a^{2} b^{2} = {(2 a^{2} - 2 a c)}^{2} + 4 a^{2} b^{2} . \end{matrix}

(3)

A jobb oldal első tagját a bal oldalra áthozva és a két négyzet különbségét szorzattá alakítva:

\begin{matrix} b^{2} (4 a^{2} - 4 a c + b^{2}) \leq 4 a^{2} b^{2}, \end{matrix}

végül minden tagot a jobb oldalra gyűjtve

\begin{matrix} 0 \leq b^{2} (4 a c - b^{2}) . \end{matrix}

(4)

Mivel itt az első tényező mindig, a második pedig a feltevés szerint nem-negatív, azért a szorzat valóban nem negatív, és mint láttuk, ebből következik az eredet egyenlőtlenség helyessége. Egyenlőség (4)-ben és ezzel együtt az előző egyenlőtlenségekben is csak a

b^{2} = 0

, vagy a

4 a c - b^{2} = 0

esetben lehetséges.
Ha azonban valamely

a

b

c

értékrendszerrel (4)-ben és így (3)-ban is egyenlőség teljesül, ebből visszafelé nem föltétlenül következik, hogy (2)-ben és így (1)-ben is egyenlőség áll fenn, mert (2) jobb oldala pozitív, a bal azonban nem föltétlenül. Így a fönt említett két esetben meg kell még vizsgálnunk, állhat-e ‐ és ha igen, milyen feltételek mellett ‐ (1)-ben egyenlőség.

b = 0

esetén (1) így alakul:

\begin{matrix} a + c - | a - c | & \leq 2 c, \\ a - c & \leq | a - c |, \end{matrix}

itt egyenlőség csak

a \geq c

esetén áll fenn.

4 a c - b^{2} = 0

esetén (1) így alakul:

\begin{matrix} a + c - | a + c | & \leq 0, \\ a + c & \leq | a + c |, \end{matrix}

itt csak

a + c \geq 0

esetén áll fenn egyenlőség. Ez azonban mindig teljesül, mert

4 a c = b^{2} \geq 0

és

a > 0

folytán

c \geq 0

.
Mindezek szerint (1) a feltevések mellett mindig teljesül, egyenlőség akkor és csak akkor áll fenn, ha vagy

\begin{matrix} 1) b = 0 és a \geq c, vagy \\ 2) 4 a c - b^{2} = 0. \end{matrix}

Megjegyzések: 1. Többen a negatív oldalakat tartalmazó

\begin{matrix} - 2 a \sqrt[]{{(a - c)}^{2} + b^{2}} \leq - (2 a^{2} - 2 a c + b^{2}) \end{matrix}

egyenlőtlenség gépies négyzetreemelésével a bizonyítandó egyenlőtlenségnek éppen az ellenkezőjét vélték ,,bizonyítani''. Ezek a versenyzők a négyzetre emeléskor hibáztak, mert hiszen pl.

- 5 < 4

, és

- 5 < - 4

, de négyzetreemelés után már a

25 > 16

egyenlőtlenség áll fenn.
2. Azokra az

a

b

c

értékrendszerekre, amelyekre (2) bal oldala negatív, az eredeti egyenlőtlenség

4 a c - b^{2}

előjelétől függetlenül teljesül. (Itt csak

a

pozitív voltát használtuk ki.)
Azokra az

a

b

c

értékrendszerekre, amelyekre (2) bal oldala nem-negatív,

4 a c - b^{2} \leq 0

és

a > 0

esetén az eredeti egyenlőtlenség fordítottja igaz;

a < 0

és

4 a c - b^{2} \geq 0

esetén az egyenlőtlenségnek szintén az ellenkezője igaz; és végül

a < 0

és

4 a c - b^{2} \leq 0

esetén az eredeti egyenlőtlenség igaz.

II. megoldás: Vonjuk ki a vizsgálandó egyenlőtlenség bal oldalát a jobb oldalból; átalakítás és összevonás után

\begin{matrix} \frac{4 a c - b^{2}}{2 a} - (a + c) + \sqrt[]{{(a - c)}^{2} + b^{2}} = \\ (5) \\ = & \sqrt[]{{(a - c)}^{2} + b^{2}} - (a - c) - \frac{b^{2}}{2 a} \geq 0. \end{matrix}

Ebből egyszerűbb kifejezés adódik, ha megszorozzuk a

\begin{matrix} \sqrt[]{{(a - c)}^{2} + b^{2}} + (a - c) + \frac{b^{2}}{2 a} \end{matrix}

(6)

értékkel. Ez a szorzó nem negatív, mert nagyobb vagy egyenlő, mint

| a - c | + (a - c)

, ami pedig nem negatív, és

0

is csak

b = 0

a \leq c

esetben lesz, de ekkor (5) bal oldala

| a - c | - (a - c) = 2 (c - a) \geq 0

, tehát a bizonyítandó állítás érvényes.
Ha (6) értéke pozitív, és megszorozzuk vele (5)-öt, akkor

\begin{matrix} (7) \\ (\sqrt[]{{(a - c)}^{2} + b^{2}} - (a - c) - \frac{b^{2}}{2 a}) \cdot (\sqrt[]{{(a - c)}^{2} + b^{2}} + (a - c) + \frac{b^{2}}{2 a}) = \\ = {(a - c)}^{2} + b^{2} - {[(a - c) + \frac{b^{2}}{2 a}]}^{2} = b^{2} - \frac{b^{2}}{a} (a - c) - \frac{b^{4}}{4 a^{2}} = \\ = \frac{b^{2} (4 a c - b^{2})}{4 a^{2}} \geq 0. \end{matrix}

Ebből következik az állítás helyessége. Az egyenlőség esetének vizsgálata ugyanúgy történhet, mint az I. megoldásban.

Megjegyzés: A (6) kifejezés átalakításából adódik, hogy

\begin{matrix} \sqrt[]{{(a - c)}^{2} + b^{2}} + (a - c) + \frac{b^{2}}{2 a} = \sqrt[]{{(a + c)}^{2} - (4 a c - b^{2})} + (a + c) - \frac{4 a c - b^{2}}{2 a} \leq 2 (a + c) . \end{matrix}

Ha a (7) bal oldalán (6) helyébe a nála nagyobb vagy egyenlő (pozitív)

2 (a + c)

-t tesszük és átosztunk vele, azt kapjuk, hogy

\begin{matrix} \sqrt[]{{(a - c)}^{2} + b^{2}} - (a - c) - \frac{b^{2}}{2 a} \geq \frac{b^{2} (4 a c - b^{2})}{8 a^{2} (a + c)}, \end{matrix}

és ebből további átalakítással

\begin{matrix} (a + c) - \sqrt[]{{(a - c)}^{2} + b^{2}} \leq (1 - \frac{b^{2}}{4 a (a + c)}) \cdot \frac{4 a c - b^{2}}{2 a} . \end{matrix}

(8)

Ez a feladatban kitűzött állításnál erősebb állítás. Ugyanis a jobb oldal első tényezőjének értéke általában kisebb 1-nél.

III. megoldás: Az (1) egyenlőtlenség bal oldala nem negatív, mert

\begin{matrix} a + c - \sqrt[]{{(a - c)}^{2} + b^{2}} = a + c - \sqrt[]{{(a + c)}^{2} - (4 a c - b^{2})} \geq a + c - | a + c | = 0, \end{matrix}

ugyanis a feltétel szerint

4 a c - b^{2} \geq 0

, és

a > 0

, tehát

c \geq 0

, és így

a + c > 0

.
Ha pozitív a bal oldal (vagyis ha

4 a c - b^{2} \geq 0

), akkor osszuk el vele mindkét oldalt. Ekkor azt kell megmutatni, hogy a mondott feltételek mellett

\begin{matrix} A = \frac{\frac{4 a c - b^{2}}{2 a}}{a + c - \sqrt[]{{(a - c)}^{2} + b^{2}}} \geq 1. \end{matrix}

(9)

Gyöktelenítsük a nevezőt:

\begin{matrix} A & = \frac{(4 a c - b^{2}) (a + c + \sqrt[]{{(a - c)}^{2} + b^{2}})}{2 a [{(a + c)}^{2} - {(a - c)}^{2} - b^{2}]} = \\ = \frac{(4 a c - b^{2}) (a + c + \sqrt[]{{(a - c)}^{2} + b^{2}})}{2 a (4 a c - b^{2})} . & (10) \end{matrix}

4 a c - b^{2}

-ről feltettük, hogy nem zérus, egyszerűsítve vele

\begin{matrix} A = \frac{a + c + \sqrt[]{{(a - c)}^{2} + b^{2}}}{2 a} \geq \frac{a + c + | a - c |}{2 a}, \end{matrix}

és itt ha a)

a \geq c

, akkor a jobb oldalon

2 a / 2 a = 1

áll,
ha pedig b)

a < c

, akkor a jobb oldal értéke

2 c / 2 a > 1

,
tehát mindig

A \geq 1

.
Egyenlőség csak az a) esetben állhat, éspedig akkor és csak akkor, ha

\begin{matrix} \sqrt[]{{(a - c)}^{2} + b^{2}} = | a - c |, azaz ha b = 0. \end{matrix}

Ha viszont a

4 a c - b^{2}

kifejezés eltűnik, akkor, mint láttuk, az eredeti egyenlőtlenség bal oldala eltűnik, és eltűnik a jobb oldal is, tehát ez esetben is helyes az állítás, mégpedig egyenlőség áll fenn.

Megjegyzés: Míg az előző megoldásból egy élesebb felső becslést sikerült kapnunk, addig ebből a megoldásból (1) bal oldalára alsó becslést kaphatunk. Ha

4 a c - b^{2}

pozitív, akkor (10)-ben egyszerűsítve vele

\begin{matrix} A = \frac{a + c + \sqrt[]{{(a - c)}^{2} + b^{2}}}{2 a} = \frac{a + c + \sqrt[]{{(a + c)}^{2} - (4 a c - b^{2})}}{2 a} . \end{matrix}

A tört értékét határozottan növeljük, ha a gyökjel alatti pozitív kivonandót elhagyjuk:

\begin{matrix} A < \frac{a + c + | a + c |}{2 a} = \frac{2 (a + c)}{2 a} = \frac{a + c}{a} . \end{matrix}

A

értékét (9)-ből beírva és átszorozva kapjuk

\begin{matrix} \frac{4 a c - b^{2}}{2 a} < [a + c - \sqrt[]{{(a - c)}^{2} + b^{2}}] \cdot \frac{a + c}{a}, \end{matrix}

vagyis

\begin{matrix} \frac{a}{a + c} \cdot \frac{4 a c - b^{2}}{2 a} < a + c - \sqrt[]{{(a - c)}^{2} + b^{2}} . \end{matrix}

(11)

Ez akkor is teljesül, ha (1)-ben

b = 0

és

a \geq c

folytán egyenlőség áll fenn; ha pedig

4 a c - b^{2} = 0

, akkor (11) is egyenlőségbe megy át, mert mindkét oldal értéke 0.
Így (9) és (11)-gyel (1) bal oldalát a következő korlátok közé szorítottuk:

\begin{matrix} \frac{a}{a + c} \cdot \frac{4 a c - b^{2}}{2 a} \leq a + c - \sqrt[]{{(a - c)}^{2} + b^{2}} \leq (1 - \frac{b^{2}}{4 a (a + c)}) \cdot \frac{4 a c - b^{2}}{2 a} . \end{matrix}

3. feladat: Az

A B C

egyenlő szárú háromszögben a

B

csúcsnál fekvő szög

n

-szer akkora, mint az

A

csúcsnál fekvő szög, ahol

n

1

-nél nagyobb egész szám. Mutassuk meg, hogy lehet a háromszöget

n - 1

egyenes vágással úgy szétvágni

n

egyenlő szárú háromszögre, hogy valamennyi háromszög szárai egyenlők legyenek.

Megoldás: Legyen a

B A C

szög nagysága

φ

, így az

A B C

szög

n φ

. Ezek különbözők, ezért a háromszög szárai vagy

A

-ban, vagy

B

-ben futnak össze. Az állítást a két esetre külön-külön bizonyítjuk.
I. eset: a szárak

A B

és

A C

, tehát a

C

csúcsnál levő szög nagysága

n φ

, a szögek összegéből

φ = 180^{\circ} / (2 n + 1)

, ez hegyesszög, mert

2 n + 1 \geq 5

, és

n φ

ugyancsak hegyesszög. ‐ Elegendő egy olyan

A_{0} B_{0} C_{0}

háromszöget adnunk, amely

n - 1

egyenes vágással

n

egyenlő szárú háromszögre bontható egyenlő hosszú szárakkal és hasonló az

A B C

háromszöghöz. Nyilvánvaló ugyanis, hogy az

A_{0} B_{0} C_{0}

-t

A B C

-be átvivő hasonlósági transzformációval valamennyi vágásszakasz megfelelőjét

A B C

-ben megszerkesztve és e háromszöget a kapott szakaszok mentén szétdarabolva ebből is

n

egyenlő szárú háromszög áll elő egyenlő hosszú szárakkal.
Egy a kívánt tulajdonsággal bíró

A_{0} B_{0} C_{0}

háromszöget egy

A_{0}

csúcsú,

φ

nagyságú szögből kiindulva a következő,

n + 1

lépésből álló és lépésenként 1‐1 újabb segédpontot előállító szerkesztéssorozattal kaphatunk. A segédpontokat rendre

A_{1}, A_{2}, ..., A_{n}, A_{n + 1}

-gyel jelöljük. Első lépésül

A_{0}

-ból egy tetszés szerinti

A_{0} A_{1} = d

szakaszt mérünk a szög egyik szárára (1. ábra, ezen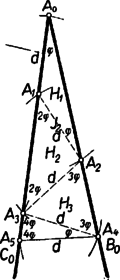

n = 4

1. ábra

A 2. lépésben

A_{1}

körül

d

sugárral kört írva

A_{2}

-ként vesszük e körnek a szög másik szárán levő,

A_{0}

-tól különböző metszéspontját. A további pontokat váltakozva a szög egyik és másik szárából metsszük ki az utoljára kapott pont körül

d

sugárral írt körívvel és mindig úgy, hogy azok a korábbi metszéspontoktól különbözők legyenek. Így

A_{3}

gyanánt az

A_{2}

körül

d

sugárral írt körnek a szög első,

A_{0} A_{1}

szárán levő,

A_{1}

-től különböző metszéspontját vesszük. Az

n + 1

-edik lépés után

A_{n}

-t

B_{0}

-nak,

A_{n + 1}

-et

C_{0}

-nak véve előttünk áll a kívánt

A_{0} B_{0} C_{0}

háromszög, és ezt az

A_{1}

-től

A_{n}

-ig terjedő egymás utáni

n - 1

segédpontpárt összekötő

n - 1

egyenlő szakasz darabolja fel a kívánt módon.
Mivel az

A_{0}

-nál levő

φ

szög hegyesszög, azért

A_{2}

valóban a másik száron jön létre. Az

A_{1} A_{0} A_{2} = H_{1}

háromszög egyenlő szárú, így

A_{2}

-nél levő szöge is

φ

, tehát

A_{1}

-nél levő külső szöge

φ + φ = 2 φ

. ‐ Ez is hegyesszög, ezért

A_{3}

A_{0}

-tól távolabb jön létre, mint

A_{1}

. Így az említett külső szög az

A_{2} A_{1} A_{3} = H_{2}

egyenlőszárú háromszögnek belső szöge, tehát

H_{2}

-nek

A_{3}

-nál levő szöge is

2 φ

, továbbá

H_{2}

kívül áll

H_{1}

-en,

A_{1} A_{2}

oldaluk közös,

A_{1}

-be befutó

A_{1} A_{3}

és

A_{1} A_{0}

oldalaik egymás meghosszabbításai, így együtt kitöltik az

A_{0} A_{2} A_{3} = J_{2}

háromszöget. Ezért az

A_{1} A_{3} A_{2}

szög

J_{2}

-nek is szöge, ennélfogva

J_{2}

-nek

A_{2}

-nél levő külső szöge

φ + 2 φ = 3 φ

. ‐ Ha

n > 2

, vagyis

n \geq 3

, akkor

3 φ

is hegyesszög, így

A_{4}

távolabb van

A_{0}

-tól, mint

A_{2}

. Ezért az

A_{3} A_{2} A_{4} = H_{3}

egyenlő szárú háromszög kívülről csatlakozik

J_{2}

-höz és

A_{4}

-nél levő szöge is

3 φ

, egyenlő az utóbbi külső szöggel. Az

A_{3} A_{4} A_{2}

szög a

J_{2}

és

H_{3}

-ból összetevődő

A_{0} A_{3} A_{4} = J_{3}

háromszögnek is szöge, így

J_{3}

-nak

A_{3}

-nál levő külső szöge

φ + 3 φ = 4 φ

.
Teljes indukcióval minden

k \leq n

-re könnyű belátni, hogy az

A_{k} A_{k - 1} A_{k + 1} = H_{k}

egyenlő szárú háromszögben

A_{k} A_{k - 1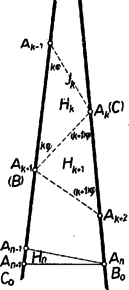} A_{k + 1} ∢ = A_{k} A_{k + 1} A_{k - 1} ∢ = k φ

(2. ábra).

2. ábra

Ennek helyességét

k = 1, 2

-re és

n \geq 3

mellett

k = 3

-ra az előzőkben láttuk. Ha már most

k

olyan az

n

-nél kisebb szám, amelyre állításunk érvényes, akkor érvényes

k + 1

-re is. Ugyanis

k < n

folytán

k + 1 \leq n

, és így a műveletsorozat még folytatódik. Az

A_{0} A_{k} A_{k + 1} = J_{k}

háromszög

A_{k}

-nál levő külső szöge

(k + 1) φ \leq n φ < 90^{\circ}

, ezért az

A_{k + 1}

körüli

d

sugarú körrel az

A_{0} A_{k}

szárból kimetszett

A_{k + 2}

távolabb van

A_{0}

-tól, mint

A_{k}

, tehát az

A_{k + 1} A_{k} A_{k + 2} = H_{k + 1}

egyenlő szárú háromszög kívülről csatlakozik

J_{k}

-hoz. Így

J_{k}

-nak

A_{k}

-nál levő

(k + 1) φ

nagyságú külső szöge

H_{k + 1}

-nek belső szöge, tehát

A_{k} A_{k + 2} A_{k + 1} ∢ = A_{k + 2} A_{k} A_{k + 1} ∢ = (k + 1) φ

. Ezek szerint állításunk érvényessége valóban öröklődik minden az

n

-nél kisebb

k

-ról

k + 1

-re.
Tekintsük most már a

J_{n} = A_{0} A_{n} A_{n + 1} = A_{0} B_{0} C_{0}

háromszöget. Ebben a fentiek szerint

A_{0} C_{0} B_{0} ∢ = A_{0} A_{n + 1} A_{n} ∢ = A_{n - 1} A_{n + 1} A_{n} ∢ = n φ

, és ezért

A_{0} B_{0} C_{0} ∢ = 180^{\circ} - φ - n φ = (2 n + 1) φ - (1 + n) φ = n φ

. Így

J_{n}

egyenlő szárú, a szögek egyenlősége folytán hasonló az adott

A B C

háromszöghöz és maradéktalanul szétvágható a

H_{1}, H_{2}, ..., H_{n}

egyenlő szárú háromszögekre. A szerkesztéssorozat első és utolsó lépése, az

A_{0} A_{1}

és

A_{n} A_{n + 1}

szakasz nem vágandó, tehát a vágások száma

(n + 1) - 2 = n - 1

. Mindezek szerint

J_{n}

-nek megvan a kívánt tulajdonsága. Ezt kellett megmutatnunk.
Továbbhaladás előtt vegyük észre, hogy az

A_{0} B_{0} C_{0}

háromszögben

B_{0} C_{0} = A_{n} A_{n + 1} = d

. Ennek alapján megtakaríthatjuk a hasonlósági transzformációt: a fenti szerkesztéssorozatot az adott háromszögben

A

-ból kezdve és

d = B C

-vel végrehajtva azonnal a kívánt felbontást kapjuk. Így

A_{n}

és

A_{n + 1}

kitűzése elmarad. A szerkesztéssorozatot fordított sorrendben, azaz

B

vagy

C

-ből kezdve is végrehajthatjuk, ilyenkor

A_{n - 1}

az első szerkesztett pont.
Vegyük észre azt is, hogy szerkesztéssorozatunk első

k + 1

lépésével, ill. az

A_{1} A_{2} ... A_{k - 1} A_{k}

vágássorozat

k - 1

vágásával, az

A_{0} A_{k} A_{k + 1} = J_{k}

(nem egyenlő szárú) háromszöget is az előírt tulajdonságú háromszögekre daraboltuk (itt

A_{k} A_{k + 1}

nem vágandó, mert

J_{k}

határának tekintjük). A felhasznált feltételeket áttekintve látjuk, hogy a következő általánosabb tételt bizonyítottuk be: Minden olyan

A B C

háromszög, melyben a

B

csúcsnál hegyes szög van és ez

k

-szor akkora, mint az

A

csúcsnál levő szög, ‐ ahol

k

az 1-nél nagyobb egész szám, ‐ szétvágható

k - 1

egyenes vágással

k

számú olyan egyenlő szárú háromszögre, hogy valamennyi rész-háromszög szárai egyenlők; a vágásszakaszok hossza a

B C

oldallal egyenlő. (Az első vágást célszerű

C

-ből indítani; de indulhat páros

k

esetén az

A B

oldal, páratlan

k

esetén az

A C

oldal azon

A_{1}

pontjából is, melyre

A A_{1} = B C

.
II. eset: a szárak

B A

és

B C

, a

C

-nél levő szög

φ

. Az állítást

n

párossága szerint két alesetben bizonyítjuk.

II/1. aleset:

n

páratlan. Legyen

n = 2 j - 1

, ahol

j > 1

, egész szám, így a szögek összegéből

φ = 180^{\circ} / (2 j + 1)

. A bizonyítást visszavezethetjük az I. esetre. Mérjük fel az

A B

szárat

A

-tól az

A C

alapra (3. ábra).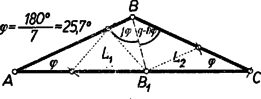

3. ábra

Az előálló

B_{1}

végpont az

A C

szakaszon van, mert

n φ > φ

folytán

A C > A B

. A háromszöget

B B_{1}

mentén kettévágva az

A B B_{1} = L_{1}

és

C B B_{1} = L_{2}

háromszögekre már alkalmazhatjuk a fenti általános tételt. Ugyanis

L_{1}

egyenlő szárú, és a

B B_{1}

alapon levő szögeinek nagysága

(180^{\circ} - φ) / 2 = (2 j + 1 - 1) φ / 2 = j φ = j \cdot p B A B_{1} ∢

. Ennélfogva

L_{2}

-ben

C B B_{1} ∢ = C B A ∢ - B_{1} B A ∢ = (2 j - 1) φ - j φ = (j - 1) φ = (j - 1) \cdot B C B_{1} ∢

. Továbbá a

B

-nél levő részszögek hegyesszögek, mert az

A B B_{1}

szög egy egyenlő szárú háromszögnek alapon levő szöge, a

C B B_{1} ∢ = (j - 1) φ

pedig kisebb

A B B_{1} ∢ = j φ

-nél. A vágásszakasz hossza

L_{1}

és

L_{2}

-ben egyaránt

B B_{1}

, mint az

A

, ill.

C

-nél levő

φ

szöggel szemben fekvő oldal. A vágások száma

1 + (j - 1) + (j - 2) = 2 j - 2 = n - 1

, a létrejövő háromszögek száma pedig

j + (j - 1) = 2 j - 1 = n

, amint bizonyítanunk kellett.
II/2. aleset:

n

páros:

n = 2 j

, ahol

j \geq 1

, egész szám. Vágjuk ketté az

A B C

háromszöget a

B

csúcsból induló

B B_{2}

magasságvonallal (4. ábra).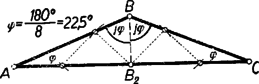

4. ábra

A létrejött egybevágó

A B B_{2}

és

C B B_{2}

derékszögű háromszögek

B

-nél levő szögei hegyesszögek és

n / 2 = j

-szer akkorák, mint az

A

, ill.

C

-nél fekvő szögek. Így a két rész-háromszög a fenti tétel szerint az előírásnak megfelelően feldarabolható (ill.

j = 1

, azaz

n = 2

esetén már fel is van darabolva), tehát az eredeti háromszög is. A vágásszakaszok hossza

B B_{2}

, a vágások száma az egész háromszögben

1 + 2 (j - 1) = 2 j - 1 = n - 1

, és az egyenlő szárú rész-háromszögek száma

2 j = n

az állításnak megfelelően. Ezzel a bizonyítást befejeztük.

Megjegyzés. A feldarabolhatóság bizonyításában az I. esetben a

B

-nél levő

n φ

, szög csúcsából kiinduló vágással is kezdhettük volna vágási sorozatunkat. Így be kellett volna bizonyítanunk, hogy az utolsó vágás utáni maradék-háromszög ugyancsak egyenlő szárú.

¹A feladat tartalmának megfelelően elég ,,természetes szám'' helyett röviden ,,szám''-ot mondanunk.

²Másképpen: e számok $100 ... 0$ -tól $199 ... 9$ -ig terjednek, ahol a 0-ok, ill. 9-esek száma $n$ , ‐ így számuk $199 ... 9 - 9 ... 99 = 100 ... 0 = 10^{n}$ .

³Szó szerint: visszafutó; az előzőre támaszkodó.