| Cím: | Megjegyzés az 596. gyakorlathoz | ||
| Szerző(k): | Bakos Tibor | ||
| Füzet: | 1960/november, 108 - 109. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
| Hivatkozás(ok): | Feladatok: 1959/november: 596. matematika gyakorlat Feladatok megoldásai: 1960/október: 596. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 1 Alább bemutatunk egy más természetű bizonyítást arra, hogy az 596. gyakorlat megoldása I. 3. pontjában felsorolt a), b), c) rendszereken kívül nincs más 4 pontból álló síkbeli pontrendszer. (Az egyenlő oldalú háromszögekre nem leszünk tekintettel.) ‐ Készítsünk táblázatot a mondott három rendszerről úgy, hogy mindegyik szakaszuk részére egy sort és mindegyik háromszögük részére egy oszlopot nyitunk, és ebben a háromszögek és száraik közti kapcsolatot úgy tüntetjük fel, hogy pl. az háromszög oszlopa és a , szárak sora közös mezejére egy jelet teszünk, elég pl. egy pontot. Jellegzetesebbé válnak e táblázatok, ha a berajzolt pontok ugyanazon sorba, ugyanazon oszlopba eső párjait egyenes szakaszokkal összekötjük; ezeket az összekötéseket a továbbiakban fel is használjuk (1. ábra). 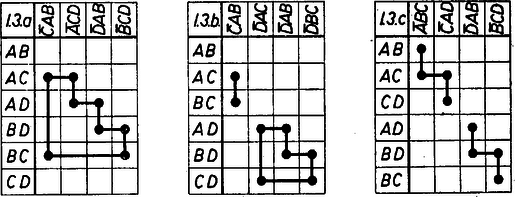 Így ugyancsak pontokból álló, de az eredeti pontrendszerektől különböző, újfajta szemléletes képet kaptunk az egyenlő szakaszok számáról és eloszlásáról. Nevezzük a kapott vonalrendszereket az eredeti ábrák sémáinak. Ha a séma vonalai mentén pontról pontra haladunk, akkor az eredeti pontrendszer azon szakaszairól tudjuk, hogy egyenlők, amelyek soraiba így egymásból eljuthatunk. Ha volna az I. 3-ban látottakon kívül további ilyen pontrendszer, nyilván ahhoz is lehetne hasonló sémát készíteni. Kérdezhetjük tehát, lehetséges-e további ilyen séma ? Tisztázzuk evégett, hogy megfordítva milyen sémákhoz tudunk pontrendszert szerkeszteni. Minden séma 8 pontból áll legfeljebb 6 sorba és pontosan 4 oszlopba rendezve; oszloponként 1 pontpár, tehát oszloponként pontosan egy összekötés van. E pontpárok csak olyan sorpárokban állhatnak, amelyekhez tartozó szakaszoknak egyik végpontjuk közös. Így ha a táblázat soraiba a pontrendszer szakaszai be vannak írva, ebből megállapíthatjuk az oszlopok háromszögeit. Ha pl. 2 egymás fölötti pont a és szakaszok sorában áll, akkor oszlopunk a háromszöghöz tartozik. Eszerint 2 oszlop 4 pontja nem adhatja egy téglalap csúcsait, különben ugyanis a 2 oszlophoz ugyanaz a háromszög tartoznék. Soronként legfeljebb 2 pont áll, mert a pontrendszer minden szakasza csak 2 háromszögnek oldala, ‐ de nem is mindig szára. Így soronként legfeljebb 1 összekötés van, továbbá a 8 pont legalább sorra oszlik el. Ezek szerint a séma minden pontja legfeljebb 2 ponttal lehet összekötve. Sémáink 1 vagy 2 összefüggő részből állnak, ezeket zártnak vagy nyitottnak mondjuk aszerint, hogy nincs, ill. van végpontjuk. Nyitott sémarésznek a végpontokba befutó összekötései ,,függőlegesek'', mert oszlopbeli összekötése minden sémapontnak van. Ezért nyitott sémarész összekötéseinek száma páratlan, mert a kötések váltakozva függőlegesek és ,,vízszintesek''; másrészt az összekötések száma 1-gyel kevesebb, mint a sémarész pontjainak száma. Hasonlóan zárt sémarészben az összekötések száma páros, éspedig ugyanannyi, mint a sémarész pontjainak száma. Láttuk, hogy sémarész nem lehet téglalap, tehát zárt sémarész legalább 6 összekötést tartalmaz. Keressük most már azokat a számunkra értelmezhető sémákat, melyek pontjai 6 sorból valók. Ezekben sorra jut 1‐1 ,,többletpont'', tehát 2 vízszintes összekötést tartalmaznak, bennük az összekötések összes száma . Így 2 nyitott részből állnak, mert az összekötések száma a pontokéhoz képest hiányt mutat. Ilyen az I. 3. c) séma két 3-tagú résszel, de elképzelhető a 2. ábra sémája is, melyen a részek összekötéseinek száma 1 és 5. 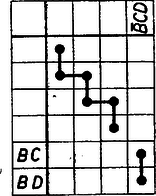 ‐ Tartozik-e ehhez pontrendszer ? Az 1-tagú rész két pontja tartozzék pl. a háromszöghöz, másképpen a , szakaszpárhoz. Így az 5-tagú rész összekötései folytán a 4 további szakasz egyenlő: , tehát az háromszög egyenlő oldalú és a háromszög köré írt kör középpontja. Ezek szerint az új sémához tartozik pontrendszer, de ez nem új, hanem a többlet-egyenlőségeket mutató I. 3. b'). Ha a séma 8 pontja 5 sorra oszlik el, akkor sorra jut 1‐1 többletpont, az összekötések száma . Ha feltesszük, hogy van zárt rész, az I. 3. b)-re jutunk, ha pedig nincs, akkor az ugyancsak ismert I. 3. ) rendszerre, mert a 3. ábra szerint 5 szakasz egyenlő. 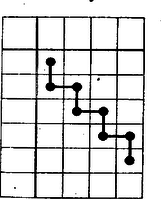 Még be kell azonban látnunk, hogy a I. 3. b) séma mellől a betűzést törölve azt lényegében csak egyféleképpen lehet visszaállítani. Valóban, a 4. és 6. sort , ill. sorának véve a zárt sémarész alapján a 2. oszlop egyértelműen a háromszögé, ennélfogva a 3. oszlop csak az háromszögé lehet, mert másodszor ebben lép fel, a 4. oszlop pedig ugyanígy csak a háromszögé. Így az 5. sor és -nek közös szakaszához tartozik, tehát , vagyis , , egy a körül írt körön vannak. Az háromszög egyenlő szárú mivoltát a séma 1 tagú része biztosítja, bármelyik csúcs lehet a főcsúcs. Hasonlóan látható be, hogy a séma 8 pontját 4 sorba rendelve összekötés van, így sem nyitott sémarész nem lehet, sem több darabból nem állhat a séma, végül a betűzés is ‐ két sor szakaszának megválasztása után ‐ egyértelműen meghatározható, tehát nem kapunk új pontrendszert. Ezzel a bizonyítást befejeztük. Elvileg esetére is szerkeszthetünk sémákat, ezek azonban egyre bonyolultabbak 1Lásd a megoldást K. M. L. XXI. (1960), 66. o. |