Cím: 1959. évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1960/február, 42 - 49. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Bizonyítsuk be, hogy ha x, y, z különböző egész számok, n pedig nem negatív egész szám, akkor

xn(x-y)(x-z)+yn(y-x)(y-z)+zn(z-x)(z-y)(1)
értéke egész szám.
 

I. megoldás. Azt fogjuk megmutatni, hogy a kifejezést közös nevezőre hozva a számláló osztható a nevezővel, közelebbről azt, hogy a nevező tényezői kiemelhetők a számlálóból, a visszamaradó tényező x, y, z-nek egész együtthatós polinomja. Így ha x, y, z egész, akkor a kifejezés értéke is egész szám.
A közös nevezőre hozott alak
xn(y-z)+yn(z-x)+zn(x-y)(x-y)(x-z)(y-z).(2)
Itt n=0-ra a számláló
(y-z)+(z-x)+(x-y)=0,
s így 0 a kifejezés értéke. Másrészt ebből
x-y=-(y-z)-(z-x).
Ezt felhasználva a számláló tetszés szerinti n-re a következőképpen alakítható:
(xn-zn)(y-z)+(yn-zn)(z-x).
Ez n=1-re 0-t ad, ha pedig n≥2, akkor (x-z)(y-z)-t, kiemelve a következőt kapjuk:
(x-z)(y-z)[xn-1+xn-2z+...+xzn-2+zn-1--yn-1-yn-2z-...-yzn-2-zn-1]==(x-y)(x-z)(y-z)[(xn-2+xn-3y+...+xyn-3+yn-2)++z(xn-3+...+yn-3)+...+zn-2].


Itt a szögletes zárójelben x, y, z-nek egész együtthatós polinomja áll állításunknak megfelelően. (Az n=2 esetben a szögletes zárójelben csak az utolsó tag, az n=3 esetben pedig csak az első kifejezés és az utolsó tag lép fel.)
 

Megjegyzés. 1. Ha n≥2, a szögletes zárójelben egyszerű felépítésű polinom keletkezett: azoknak az x, y, z hatványait tartalmazó szorzatoknak az összege, amelyekben a hatványkitevők összege n-2.
2. Sok versenyző a feladat állítását bizonyítottnak vélte annyit mutatva meg, hogy a (2) alatti kifejezés számlálója osztható külön-külön az x-y, x-z, y-z egészekkel. Ebből azonban csak akkor következtethetnénk arra, hogy ezek szorzatával is osztható a számláló, ha a három különbség semelyik kettőjének nem volna 1-nél nagyobb közös osztója; ez azonban általában nem teljesül.
Helyessé tehető ez az okoskodás, ha a számlálót és nevezőt az x, y, z változók polinomjának tekintjük. Ekkor az x-y, x-z, y-z polinomoknak nincs változót tartalmazó közös osztója, és mindegyik kiemelhető a számlálóban szereplő polinomból. Ebből az egész együtthatós polinomok körében is következik, hogy a három kifejezés szorzata is kiemelhető a számlálóból. Néhány versenyző ezen az úton helyes bizonyítást adott a feladat állítására, ezzel azonban lényegesen mélyebb tételt használt fel bizonyítatlanul, mint a bizonyítandó állítás.
Helyessé tehető azonban ez a gondolatmenet a gyöktényezők kiemelésére vonatkozó tételt a következő alakban használva fel: Ha egy f(x) polinomnak gyöke a t szám, akkor f(x) felbontható x-t-nek és egy polinomnak a szorzatára. Ha f(x) egész együtthatós, és t is egész szám, akkor x-t szorzója is egész együtthatós polinom. Ez könnyen leolvasható a gyöktényező kiemelésére vonatkozó szokásos bizonyításokból például a következő módon: Legyen
f(x)=a0xn+a1xn-1+...+an-1x+anésf(t)=0.
Ekkor
f(x)=f(x)-f(t)=a0(xn-tn)+a1(xn-1-tn-1)+...+an-1(x-t)==(x-t)[a0(xn-1+xn-2t+...+tn-1)+a1(xn-2+...+tn-2)+...+an-1]==(x-t)[a0xn-1+(a0t+a1)xn-2+(a0t2+a1t+a2)xn-3+...++(a0tn-1+a1tn-2+...+an-1)].


Ha itt az ai együtthatók és t egész szám, akkor nyilvánvalóan egész együtthatós a szögletes zárójelben levő kifejezés is.
Ennek alapján a feladat állítása így látható be:
 

II. megoldás. A (2) kifejezés számlálója 0, ha n értéke 0 vagy 1. Ha n≥2, akkor rendezzük a kifejezés számlálóját x hatványai szerint, és végezzük el a kínálkozó kiemelést:
xn(y-z)-x(yn-zn)+yz(yn-1-zn-1)=(3)=(y-z)[xn-x(yn-1+yn-2z+...+zn-1)+yz(yn-2+...+zn-2)].


(Itt n=2 esetén a szögletes zárójelben az utolsó tag utolsó tényezőjén az 1 számot kell érteni.) Tekintsük ezt most az x változó polinomjának, y és z pedig jelentsenek adott különböző egész számokat. Ekkor (3) bal oldala eltűnik az x=y helyen, így a jobb oldal második tényezője is, mert y és z különböző. Ez a tényező egész együtthatós és y is egész, így kiemelhető az x-y tényező és kiemelése után egy egész együtthatós polinom marad vissza.
Ez a polinom eltűnik az x=z helyen, mert (3) bal oldala eltűnik, viszont a jobb oldalon az előző kiemelés után keletkezett (y-z)(x-y) szorzat nem tűnik el, mivel y és z különböző. Így kiemelhető még az x-z tényező is és ismét x egész együtthatós polinomja marad vissza. Ha az így átalakított számlálóban x helyébe is az adott egész értéket helyettesítjük, azt kapjuk, hogy a számláló az (y-z)(x-y)(x-z) szorzatnak egy egész többszöröse, tehát a (2) kifejezés egész szám.
 

III. megoldás. Jelöljük az (1) kifejezést Pn(x,y,z)-vel. Teljes indukcióval fogjuk bizonyítani, hogy ez az x, y, z változók egész együtthatós polinomja.
Az állítás n=0-ra igaz, mert P0(x,y,z) azonosan 0.
Tegyük fel, hogy valamilyen n=k értékre Pk(x,y,z) egész együtthatós polinom. Kiküszöbölve Pk+1(x,y,z)-ből és Pk(x,y,z)-ből a harmadik tagot a következő azonossághoz jutunk:
Pk+1(x,y,z)-zPk(x,y,z)=xk+1-zxk(x-y)(x-z)+yk+1-zyk(y-x)(y-z)=xk-ykx-y,
azaz
Pk+1(x,y,z)=zPk(x,y,z)+(xk-1+xk-2y+...+yk-1),(4)
ahol k=0-ra a zárójelben álló összeg 0-val helyettesítendő. Ebből azonnal következik, hogy Pk(x,y,z)-vel együtt Pk+1(x,y,z) is x, y, z egész együtthatós polinomja. Állításunk tehát minden nem negatív egész n-re érvényes.
 

Megjegyzés. A (4) azonosság mindjárt módot is ad a Pn(x,y,z) polinomok lépésről lépésre történő ‐ úgynevezett rekurzív ‐ meghatározására. Megkaphatjuk ebből Pn(x,y,z) explicit előállítását is, teljes indukcióval bebizonyíthatjuk az I. megoldáshoz fűzött 1. megjegyzés állítását.
 

IV. megoldás. Az (1) kifejezést tekinthetjük a
Pn(k)(x1,x2,...,xk)=x1n(x1-x2)(x1-x3)...(x1-xk)++x2n(x2-x1)(x2-x3)...(x2-xk)+...+xkn(xk-x1)(xk-x2)...(xk-xk-1)


kifejezések speciális esetének, ha k=3. Értelem szerint Pn(x1)-en x1n-t értjük. Az alábbi meggondolások erre az esetre is érvényesek. Megmutatjuk, hogy ezek a kifejezések minden k-ra és tetszés szerinti nem negatív egész n-re a változók egész együtthatós polinomjai.
A bizonyítás történhetik a változók számára vonatkozó teljes indukcióval. A k=1 értékre
Pn(1)(x1)=x1n
az x1 változó egész együtthatós polinomja.
Tegyük fel, hogy ha k valamilyen l-1 értékkel egyenlő (ahol l-1≥1), akkor Pn(l-1)(x1...,xl-1) a változóinak egész együtthatós polinomja. Ekkor képezzük a
Pn(l-1)(x1,...,xl-2,xl-1)-Pn(l-1)(x1,...,xl-2,xl)
kifejezést. Itt az xin számlálójú tag mindkét kifejezésben fellép, ha l>2 és i≤l-2, a nevezők pedig egyenlővé válnak, ha az első törtet xi-xl-lel, a másodikat xi-xl-1-gyel bővitjük. Ekkor a számlálóban
xin(xi-xl)-xin(xi-xl-1)=xin(xl-1-xl)
lesz, tehát a két tört összevonásával az
xin(xl-1-xl)(xi-x1)...(xi-xi-1)(xi-xi+1)...(xi-xl-1)(xi-xl)
tag keletkezik. Az első, ill. második kifejezés utolsó tagját xl-1-xl-lel bővítve így alakítjuk át:
xl-1n(xl-1-x1)...(xl-1-xl-2)=xl-1n(xl-1-xl)(xl-1-x1)...(xl-1-xl-2)(xl-1-xl),
ill.
-xln(xl-x1)...(xl-xl-2)=xln(xl-1-xl)(xl-x1)...(xl-xl-2)(xl-xl-1).
Így a következő azonosságra jutunk, kiemelve a minden tagban közös (xl-1-xl) tényezőt:
Pn(l-1)(x1,...,xl-2,xl-1)-Pn(l-1)(x1,...,xl-2,xl)=(xl-1-xl)Pn(l)(x1,...,xl).(5)

Itt a bal oldalon Pn(l-1)(x1,...,xl-2,xl-1) és Pn(l-1)(x1,...,xl-2,xl) az indukciós feltevés szerint a változók egész együtthatós polinomja; az utóbbi úgy nyerhető az előbbiből, hogy xl-1 helyébe xl-et írunk. Így az egyiket xl-1, a másikat xl hatványai szerint rendezve a két kifejezésben xl-1, ill. xl egyenlő hatványainak megegyezik az együtthatója. A különbségben ezeket a közös együtthatókat kiemelve xl-1r-xlr alakú különbségek lépnek fel. Ezek mindegyikéből, s így (5) bal oldalából is kiemelhető az xl-1-xl tényező. A visszamaradó tényező, ami (5) szerint Pn(l)(x1,...,xl)-et adja, az x1,...,xl változók egész együtthatós polinomja. Ezzel indukciós bizonyításunkat befejeztük.
 

Megjegyzések. 1. A bizonyítást lépésről lépésre követve az is könnyen bizonyítható teljes indukcióval, hogy Pn(k)(x1,...,xk) az x1,...,xk változók hatványaiból képezett összes olyan szorzatok összege, amelyekben a kitevők összege n-k+1, ha n≥k; Pn(k) azonosan egyenlő 1-gyel, ha n=k-1, ha pedig n≤k-1, akkor 0-val.
2. Az eddigi bizonyítások mindegyike felhasználta az
ak-bk=(a-b)(ak-1+ak-2b+...+abk-2+bk-1)
azonosságot. A következő ‐ lényegében Arató Péter dolgozatából származó ‐ megoldásban erre sincs szükség.
 

V. megoldás. A
(t-x)(t-y)(t-z)=t3-(x+y+z)t2+(xy+xz+yz)t-xyz
kifejezés, mint t polinomja nyilván eltűnik a t=x, t=y, t=z helyeken és ugyanez áll a kifejezés tn-szeresére is. Így ha t az x, y, z akármelyikét jelenti, azonosan teljesül, hogy
tn+3=tn+2(x+y+z)-tn+1(xy+xz+yz)+tnxyz,(6)(t=x,vagyt=y,vagyt=z)


(ami különben közvetlenül is könnyen belátható).
Jelöljük a feladatban szereplő kifejezést Pn(x,y,z)-vel, amint a III. megoldásban is tettük, akkor Pn+3(x,y,z) tagjainak számlálójában felhasználva a (6) azonosságokat, a következő azonossághoz jutunk:
Pn+3(x,y,z)=(x+y+z)Pn+2(x,y,z)-(xy+xz+yz)Pn+1(x,y,z)++xyzPn(x,y,z).


Ebből látjuk, hogy ha kifejezésünk n három egymásutáni egész értékére a változók egész együtthatós polinomja, akkor ugyanez áll minden nagyobb n egész számra is. Mivel pedig P0(x,y,z)=P1(x,y,z)=0, P2(x,y,z)=1, így Pn(x,y,z) minden nem negatív egész n-re az x, y, z változók egész együtthatós polinomja.
 

Megjegyzés. Az V. megoldás módszerével is bizonyítható a IV. megoldásban szereplő általánosabb állítás tetszés szerinti adott k-ra, csak ekkor n=0,1,...,k-1-re kell meghatározni Pn(k)(x1,x2,...,xk) értékét.
 

2. feladat. Megmértük egy vízszintes terepen álló antennatorony emelkedési szögét a talppontjától 100m, 200m és 300m távolságból. A három szög összege 90∘. Milyen magas a torony?
 

Igen egyszerű trigonometriai megoldás kínálkozik a feladatra és a versenyzők mind ilyen utat is választottak.
 

I. megoldás. Jelöljük a torony magasságát méterben mérve x-szel, a látószögét 100, 200, 300m-ről rendre α, β, γ-val, ekkor
tgα=x100,tgβ=x200,tgγ=x300,
és feltétel szerint α+β+γ=90∘, tehát
tgγ=x300=tg[90∘-(α+β)]=ctg(α+β)=ctgαctgβ-1ctgα+ctgβ==100x⋅200x-1100x+200x=100⋅200-x2300x.


Innen
2x2=100⋅200,
és mivel x gyanánt csak pozitív érték jön számításba, tehát a torony magassága x=100m.
Megjegyzés. Mint többen észrevették, megoldható a feladat ugyanezzel a gondolatmenettel akkor is, ha tetszés szerinti a, b, c távolságokból mért α, β, γ látószögekről tudjuk azt, hogy összegük 90∘. Ekkor a torony magassága abc/(a+b+c).
Megoldható azonban a feladat lényegesen egyszerűbb összefüggésekre támaszkodva is.
 

II. megoldás. Sík talajon nem lényeges, hogy milyen irányból mérjük a torony látószögét az adott távolságokból, válasszuk tehát a 100, ill. 200m távolságra levő A, ill. B pontokat a toronytól egymással ellentétes irányban, a γ látószöget pedig szemléltessük úgy, hogy a B pontból az AB egyenesnek a torony C csúcsával ellentétes oldalán mérünk fel AB-re merőlegesen a torony magasságával egyenlő BD távolságot. Ekkor 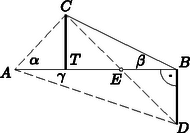BAD∢=γ, mert AB=300m.
 
 

1. ábra
 

A torony T talppontja, C csúcsa továbbá a B és D pontok meghatározta négyszög paralelogramma, mert két oldala egymással párhuzamos és egyenlő, tehát CD a TB szakaszt E felezőpontjában metszi. Eszerint ET=100m, s így TEC∢=α, az ACE háromszög egyenlő szárú. Megállapíthatjuk C-nél levő szögének a nagyságát is abból, hogy az ADBC négyszög A-nál és B-nél levő (szemben fekvő) szögeinek összege α+γ+β+90∘, a feltétel szerint 180∘-ot ad; a négyszög tehát húrnégyszög, és AD a körülírt kör átmérője, mert a B pontból 90∘-os szögben látszik. Így az ACD∢=ACE∢ szintén 90∘-os, az ACE egyenlő szárú háromszög tehát derékszögű. Ebből adódik, hogy α=45∘, így az ATC derékszögű háromszög ugyancsak egyenlő szárú, tehát a torony magassága 100m.
 

III. megoldás. Rajzoljuk meg a tornyot háromféleképpen. Két oldalról egyrészt az α és β látószögű egyenesekkel, másrészt β és γ, harmadrészt γ és α látószögű egyenesekkel (2. ábra). A keletkező három háromszögben az A1B1, B2C2, C3A3 oldalakon levő szögek összege 2α+2β+2γ=180∘, így a D1, D2, D3-nál levő szögek összege 360∘. Mivel még B1D1=B2D2, C2D2=C3D3, A3D3=A1D1, így a három háromszög egy ABC háromszöggé tehető össze. Ennek oldalai AB=300m, BC=500m, CA=400m kielégítik a
BC2=CA2+AB2
összefüggést, és ismeretes, hogy ebből következik a háromszög derékszögű volta, (a Pythagorász-tétel megfordítható) derékszöggel az A csúcsnál. Így 2α=90∘, és ebből következik, hogy a torony 100m magas.
 
 

2. ábra
 

Megjegyzés. A II. megoldás lényegesen kihasználja a feladat speciális adatait, a III. azonban csak részben. Ha ugyanis megfigyeljük, hogy az összeillesztésnél a D1, D2, D3 egybeesésével keletkező D pont az ABC háromszög beírt körének a középpontja, akkor területszámítás segítségével más távolságadatok mellett is meghatározható a torony magassága.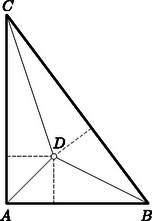
 
 

3. ábra
 

3. feladat. Három fivér egy napon látogatott meg egy beteget. Ugyanazon a napon mindegyiknek a felesége is ott járt. Egyikük sem volt ott aznap többször. Mindhárom fivér találkozott a betegágynál mindkét sógornőjével. Bizonyítandó, hogy valamelyikük a feleségével is találkozott ott.
 

I. megoldás (Kóta Gábor dolgozata nyomán). Tegyük fel, hogy pl. A és A-né nem találkozott a betegágynál. Ekkor A-né vagy elment, mielőtt férje megérkezett és ez esetben korábban távozott a betegágytól mint két sógornője, hiszen ők találkoztak a betegágynál az A-né távozása után érkező A-val, vagy pedig A-né A távozása után érkezett és ekkor későbben érkezett mint két sógornője, hiszen azoknak A távozása előtt kellett a beteghez érkezniük. Csak úgy lehet tehát, hogy egy asszony nem találkozott a férjével, ha vagy előbb távozott, mint a két sógornője, vagy később érkezett náluk.
Azonban három asszony közül legalább az egyik sem nem érkezett a másik kettő után, sem nem távozott azok távozása előtt, így legalább egynek találkoznia kellett a férjével.
 

II. megoldás. Indirekt úton bizonyítjuk a feladat állítását. Tegyük fel, hogy egyik házaspár sem találkozott a betegágynál. Ez esetben, ha pl. A előbb érkezett A-nénél, akkor el is kellett távoznia felesége érkezése előtt. Viszont találkozott B-nével, tehát B-né előbb érkezett mint A-né. B-nek felesége távozása után kellett érkeznie, csak így találkozhatott A-néval anélkül, hogy feleségével találkozott volna. Ha A a felesége után érkezett a betegágyhoz, akkor fenti meggondolásunkban férj és feleség szerepét mindenütt megcserélve szintén azt nyerjük, hogy férj és feleség a B házaspárból fordított sorrendben kellett, hogy a betegágyhoz érkezzék, mint az A házaspárból.
Ugyanezt a meggondolást megismételve egyrészt az A és C házaspárra, másrészt a B és C házaspárra azt kapjuk, hogy C és C-né fordított sorrendben kellett hogy a betegágyhoz érkezzék, mint A és A-né, de ugyancsak fordított sorrendben, mint B és B-né. Ez azonban már lehetetlen, tehát legalább egy házaspárnak találkoznia kellett a betegágynál.
 

Megjegyzés. A most ismertetett meggondolás alkalmas egy általánosabb tétel bizonyítására is. Hogy ezt könnyebben megfogalmazhassuk, előbb átfogalmazzuk az eredeti feladatot.
A három házaspár elhelyezkedhet egy kerek asztal körül pl. A, B-né, C, A-né, B, C-né sorrendben (C-né másik szomszédja A). Ekkor azt mondhatjuk: a hattagú társaság minden tagja meglátogatott (pl. másnap) egy beteg ismerőst. Mindenki csak egyszer járt ezen a napon a betegágynál és mindenki találkozott ott mind a két előző napi asztalszomszédjával. Ez csak úgy történhetett, hogy valaki házastársával (azaz a vele szemben ülővel) is találkozott.
Ez speciális esete a következő általánosabb tételnek: Egy nap n házaspár beszélgetett egy asztal körül, ahol úgy helyezkedtek el, hogy mindenki éppen házastársával szemben ült. Elhatározták, hogy másnap mindegyikük meglátogatja egy közös ismerősüket, aki beteg. A látogatás során úgy adódott, hogy mindenki találkozott a betegágynál két előző napi asztalszomszédjával és ezen a napon mindenki csak egyszer járt a betegnél. Ekkor valamelyik házaspár találkozott a betegágynál.
Tegyük fel az állítással ellentétben, hogy egyik házaspár sem találkozott, noha a többi feltételek teljesültek. Az asztalszomszédok legyenek sorra A1, A2, ..., A2n, A1, itt A1 és An+1, A2 és An+2, ..., An és A2n házastársak. Tegyük fel, hogy a betűzést úgy választottuk, hogy A1 előbb érkezett a betegágyhoz, mint házastársa, An+1 (és feltevésünk szerint el is kellett távoznia An+1 érkezése előtt).
Ekkor A2, aki találkozott A1 gyel, előbb kellett, hogy érkezzék, mint An+1. Így An+2, aki találkozott An+1-gyel, de feltevésünk szerint nem találkozott házastársával, A2-vel, csak A2 távozása után érkezhetett. Hasonlóan An+3-nak A3 távozása után kellett érkeznie és így tovább. Így azonban az n-edik lépésben azt kapjuk, hogy az A2n-nel találkozó A1 csak azután érkezhetnék a betegágyhoz, miután An-nel találkozó házastársa, An+1 eltávozott, holott abból indultunk ki, hogy A1 előbb érkezett mint An+1.
Nem lehet tehát, hogy egyik látogató se találkozzék a betegágynál a házastársával.