Cím: Az 1959. évi matematika OKTV II. fordulóján kitűzött feladatok és megoldásuk
Füzet: 1960/január, 2 - 7. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat: k-nak mely pozitív egész értékei mellett lesz a

N=36n-1-k⋅23n-2+1
kifejezés n minden pozitív egész értékére osztható 7-tel ?
 

Megoldás: Ha N valamilyen k érték mellett minden n-re osztható 7-tel, akkor n=1-re is osztható, tehát
35-2k+1=244-2k=7m.(1)
Itt a bal oldal páros, tehát a jobbnak is párosnak kell lennie. Ez akkor és csak akkor áll fenn, ha m páros: m=2m1. Így k-ra azt kapjuk, hogy
k=122-7m1=7(17-m1)+3=7m2+3.
Itt m2 tetszés szerinti egész értéke mellett fennáll (1) az m=34-2m2 értékkel.
Megmutatjuk másfelől, hogy N minden n-re 7-tel osztható számmal tér el az n=1-hez tartozó értéktől. Valóban
N-(35-2k+1)=35(36(n-1)-1)-2k(23(n-1)-1),
és a jobb oldal első különbsége osztható 36-1=(33-1)(33+1)=26⋅28-cal, tehát 7-tel is, a második tag pedig osztható 23-1=7-tel, így az egész különbség is.
Azt kaptuk tehát, hogy N akkor és csak akkor osztható minden n-re 7-tel, ha ez az n=1-hez tartozó értékére teljesül, ehhez pedig szükséges és elegendő is, hogy k 7-tel osztva 3-at adjon maradékul.
 

2. feladat: Adva vannak az e, f párhuzamos egyenesek és köztük az O pont; O távolsága e-től a, f-től b. Az O-n áthúzott g egyenes e-t E-ben, f-et F-ben metszi. F-ben merőlegest állítunk g-re, és erre az e-vel való metszéspontja irányában felmérjük az OE szakaszt, ennek végpontja P. Mi a P pont mértani helye, ha g az O körül forog ?
 

I. megoldás: Legyen g-nek az f-re merőleges helyzete g0, ennek metszéspontjai e, f-en E0, F0. Ekkor a kérdéses merőleges maga f, így az e-vel való metszéspont nem létezik, P nem szerkeszthető egyértelműen; azonban f-nek F0-tól OE0=a távolságra fekvő P01 és P02 pontjait tágabb értelemben a mértani helyhez tartozóknak tekinthetjük. ‐ Elegendő g-nek azon helyzeteivel foglalkoznunk, amelyek f-et az F0P01 félegyenesén metszik, mert a mértani helynek az így mellőzött pontjait a figyelembe vettekből g0-ra való tükrözéssel megkaphatjuk, hiszen g minden mellőzött helyzetének megvan a tükörképe a figyelembe vett helyzetek között.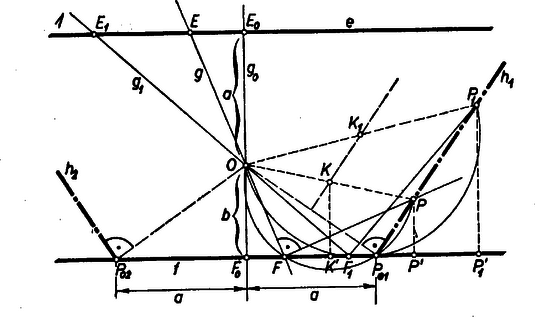
 
 

Legyen a forgó egyenesnek egy g helyzetében OP felezőpontja K, P és K vetülete f-en P', K'. Ekkor az FPP' és OEE0 derékszögű háromszögek egybevágók, mert FP=OE, továbbá F, ill. O-nál levő szögeik merőleges szárú hegyes szögek, és ezért egyenlők. Így FP'=OE0=a=F0P01 és F a P'-től ellentétes irányban van, mint P01 az F0-tól (ugyanis az F0FP szög nagyobb az OFP szögnél, ez pedig derékszög). Ezért P01 és F tükrös párok az F0P' szakasz felező merőlegesére ‐ ami egyben az OF0P'P trapéz KK' középvonala ‐, és így KP01=KF. Másrészt K az OFP derékszögű háromszög köré írt kör középpontja. Ezek szerint e kör átmegy P01-en és ezért az OP01P szög (g bármely helyzete mellett) derékszög; más szóval P csak a P01-ben OP01-re állított merőlegesen fekhet. Tegyük hozzá: az FP szakaszok felmérési irányára tekintettel P a merőlegesnek csak azon a h1 félegyenesén lehet, amely f-nek ugyanazon partján van, mint e (és O).
Megmutatjuk, hogy a figyelembe vett g helyzetekre a keresett mértani hely éppen h1, vagyis h1 bármely P01-től különböző P1 pontja előáll g valamely helyzetéből.
g1-nek a P1-et előállító helyzetére, ill. a vele adódó E1, F1-re egyrészt a P1F1O szögnek derékszögnek, másrészt F1P1=OE1-nek kell lennie. Az első követelményből g1 egyértelműen megszerkeszthető, ehhez F1-et az OP1 átmérőjű (és P1P01O∢=90∘ folytán P01-en átmenő) Thalész-körnek f-fel való, P01-től különböző metszéspontja adja ‐ amennyiben két ilyen metszéspont van ‐, és F1≡P01, ha e kör érinti f-et. E kör K1 középpontja rajta van az F0P'1 szakasz felező merőlegesén (P'1 a P1 vetülete f-en), így F1 és P01 tükrös pontpár F0P'1 felezőpontjára, és ezért F1P'1=F0P01=OE0. Így az OE1E0 és F1P1P'1 derékszögű háromszögek egybevágók (E1 a g1 és e metszéspontja), mert O, ill. F1-nél fekvő szögük szárai páronként merőlegesek (Thalész-kör), ennélfogva OE1=F1P1 amit bizonyítani akartunk. (Teljesség kedvéért megjegyezzük, hogy F1 az F0P01 félegyenesen van, mert nem lehet sem F0-ban, sem az F0P02, félegyenesen; ugyanis F0 a körre nézve külső pont, K1 az OP0 szakasz felező merőlegesének azon a félegyenesén van, amely OP01-nek F0-val ellentétes oldalára esik, az utóbbinak pontjai pedig F0-tól távolabb vannak, mint P01-től.)
Ezek szerint a keresett mértani helyet h1 és ennek g0-ra való h2 tükörképe adja, vagyis az f egyenes F0P01=F0P02=OE0 tulajdonságú P01, P02 pontjaiban OP01, ill. OP02-re állított merőlegeseknek azok a félegyenesei, amelyek f-nek O-t tartalmazó partján vannak. P01 és P02 a mértani helynek csupán tágabb értelemben vett pontjai.
 

Megjegyzések. 1. FP'=F0P01 megállapítása után ‐ ahol a szakaszok iránya is megegyező ‐, vizsgálatunkat így is befejezhetjük: eszerint P01P'=F0F, másrészt PP'=EE0, ennélfogva PP':P01P'=EE0:F0F=OE0:OF0=a:b, azaz állandó, tehát bármely P-be P01-ből ugyanaz az irány mutat. Így azonban még hátra van ennek az iránynak a meghatározása.
2. Többen pontos rajzú próbák nélkül azt a pusztán szabadkézi vázlatra alapított sejtésüket próbálták igazolni, hogy a mértani hely kör, hiperbola, hiányos parabola, vagy két kotangens-görbe.
A versenyzők nagyobb része a koordináta-geometria módszereivel kereste a mértani hely egyenletét, gyakran elég bonyolult számításokkal, a szakaszfelmérést egyenes és kör metszésének tekintve, ami két lehetőséget ad P-re, a helyes irány megválasztása pedig diszkussziót igényel. Alább egy ezt a lépést kikerülő, részben koordináta-geometriai megoldást adunk.
 

II. megoldás: Válasszuk f-et X-, és a rá O-n át húzott merőlegest Y-tengelynek úgy, hogy O ordinátája b legyen, és legyen a kezdőpont K, továbbá e és az Y-tengely metszéspontja L. Tekintsük egyelőre azokat a g-ket, amelyek az X-tengelyt pozitív abszcisszájú F-ben metszik, és jellemezzük g helyzetét azzal a γ pozitív hegyes szöggel, amellyel O körül az Y-tengelyhez képest el van fordulva. Így F, E koordinátái: (btgγ,0), (-atgγ,b+a) és a felmérendő OE=z szakasznak az Y-tengelyre való vetülete a, az X-tengely irányára pedig 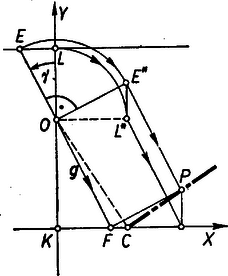LE=-atgγ.
 
 

E szakasz előírt felmérését helyettesíthetjük O körüli -90∘-os elforgatásával és O-nak F-be való eltolásával.
Így az elforgatott OE* vetületei X, Y irányára OL*=a, L*E*=atgγ, és az eltolás után P koordinátái: x=btgγ+a, y=atgγ. (f, e pontjainak ordinátája 0, ill. b+a>0, ennélfogva OE-nek e felé való felmérése P-re pozitív ordinátát ír elő; valóban y>0, mert γ>0∘.
A keresett mértani hely eddig tekintetbe vett részének egyenletét P koordinátáiból a γ paraméter kiküszöbölésével kapjuk:
tgγ=x-ab=ya-ból:y=ab(x-a),
és ehhez járul tgγ>0 helyett az y/a>0, azaz y>0 megszorítás. Ez félegyenes egyenlete, amely az X tengelyt az x=a abszcisszájú C pontban metszi (itt a kezdőpontja) és amely merőleges OC-re, mert OC iránytangense -b/a.
Hasonlóan kapjuk az X-tengelyt negatív abszcisszájú F-ben metsző g egyenesekre F(-btgγ,0) és E(atgγ,b+a)-ból P-re: x=-btgγ-a, y=atgγ (itt γ a g elfordulása Y-tól a negatív forgási irányban). Eszerint P abszcisszája az előbbinek -1-szerese, ordinátája változatlan, ez az Y-tengelyre való tükrözést jelent, ennélfogva a mértani hely hiányzó része az eddigiből az f-re O-n át húzott merőlegesen való tükrözéssel áll elő.
 

Megjegyzések. 1. A fentiekben nem ,,tiszta'' koordinátageometriai módszerrel dolgoztunk, több lépést elemi, ill. trigonometriai úton végeztünk.
2. OE-nek a g-re merőlegesen való felmérésével adódó pontot megkaphatjuk a merőleges és a g-ből (rá merőleges) OE nagyságú eltolással előálló g' egyenes metszéspontjaként is. Így azonban mindegyik említett egyenes egyenletét fel kellene írnunk, és többet kellene számolnunk. Az ,,e felé'' való eltolás révén a g'-vel az Y-ból lemetszett szakasz b-ről b+OE/sinγ=b+a/sinγcosγ-ra növekszik.
 

3. feladat: Egy ABCA'B'C' konvex hatszög csúcsai egy kör AA', BB', CC' átmérőinek végpontjai, és P a körnek a hatszög csúcsaitól különböző pontja. Legyenek P-ből az AB, BC, CA', A'B', B'C', C'A oldalra bocsátott merőlegesek talppontjai rendre Q1, Q2, Q3, Q4, Q5, Q6. Bizonyítandó, hogy a Q1Q2Q3Q4Q5Q6 hatszögnek bármelyik két egymás utáni oldala derékszöget alkot, továbbá, hogy a Q1Q4 Q2Q5, Q3Q6 szakaszok felező pontjai és P egy körön fekszenek.
 

I. megoldás: A Q1Q2Q3Q4Q5Q6=H2 hatszög bármelyik két egymás utáni oldalát ‐ három egymás utáni csúcsát ‐ az ABCA'B'C'=H1 hatszög három egymás utáni oldala ‐ négy egymás utáni csúcsa ‐ határozza meg; és az első és a negyedik csúcs egy átmérőnek két végpontja.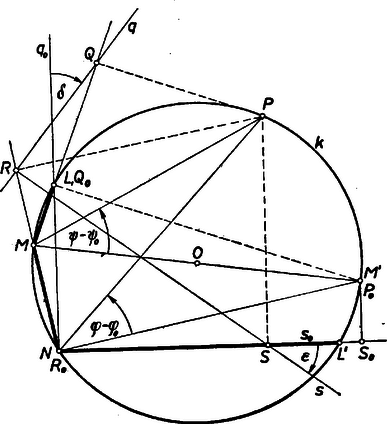
 
 

Ezért az állítás első részében elég azt bizonyítanunk, hogy ha L, M, N, L' ebben a sorrendben egy k körnek egymástól különböző pontjai, LL' a k-ban átmérő, és egy a k-n fekvő P-ből az LM, MN, NL' egyenesekre bocsátott merőlegesek talppontjai rendre Q, R, S, akkor QR=q és RS=s egymásra merőlegesek. Evégett megmutatjuk egyrészt, hogy P egy bizonyos P0 helyzetében Q0R0=q0 és R0S0=s0 merőlegesek, másrészt hogy ha P elmozdul a k-n, akkor QR=q és RS=s egymással megegyező irányban ugyanakkora szöggel fordulnak el. (L, M, N és L' sorrendje megfelel H1 konvexségének.)
Valóban, P0-ként az M-en átmenő átmérőnek M' másik végpontját véve Q0 az L-be, R0 az N-be esik, így Q0R0S0∢=LNS0∢=LNL'∢, és ez a feltevésnél fogva derékszög.
 
 

Legyen η az s (előjellel vett) hajlásszöge PR-nek attól a élegyenesétől mérve, amely MN-nek ugyanazon partján van, mint L. Az N, P, R, S pontok P bármely helyzetében húrnégyszöget határoznak meg, ebből látható, hogy η mindig egyenlő a φ=L'NP szöggel, de avval ellentétes irányú: η=-φ. Eszerint ha P a P1 helyzetből P2-be megy át, akkor a megfelelő s1-nek s2-be való δ elfordulási szögét P1R1 és P2R2 párhuzamossága folytán az η2-η1 különbség adja, és erre δ=η2-η1=-(φ2-φ1), vagyis s elfordulása egyenlő, de ellentétes irányú NP elfordulásával. (Ez nem a k-n fekvő P-re is érvényes.) ‐ Eredményünk alapján egy P2-ből szerkesztett q2-nek egy P1-ből szerkesztett q1-hez képest való ε elfordulási szöge is kiadódik: -(ψ2-ψ1), ahol ψ1 és ψ2 a ψ=NMP szög megfelelő két értékét jelöli. ‐ Most már P két helyzetének k-n P0-t és P-t véve ψ-ψ0=P0MP∢=P0NP∢=φ-φ0, eszerint ε=δ, vagyis q, s a q0, s0-hoz képest valóban ugyanannyival és ugyanazon irányban fordulnak el, és ezért SRQ∢=S0R0Q0∢, derékszög, amit bizonyítani akartunk.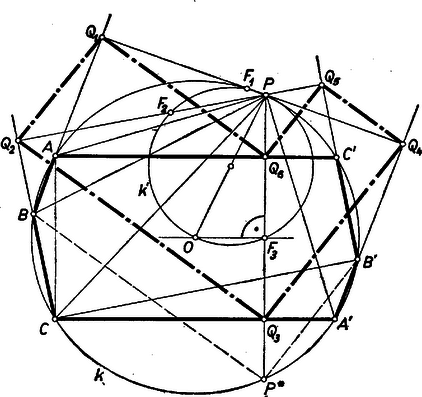
 
 

H1 mindegyik szemben fekvő oldalpárja egymással párhuzamos, mert végpontjaik, mint két átmérő végpontjai, egy téglalapnak a csúcsai; ezért a P-ből rájuk bocsátott merőlegesek azonosak, így pl. a P, Q3, Q6 ponthármas egy egyenesbe esik. Ezért a Q3Q6 szakasz F3 felezőpontja egyrészt PQ3-on fekszik, másrészt az ACA'C' téglalapnak az AC-re merőleges tengelyén, amely k-nak átmérője, tehát F3-ból az OP sugár derékszögben látszik, F3 az OP átmérőjű k' Thalész-körnek pontja. (Az utóbbi akkor is áll, ha F3 éppen P-be esik.) Ugyanez áll a Q1Q4, Q2Q5 szakaszok F1, F2 felezőpontjára. Ezzel bebizonyítottuk az állítás második részét, és egyben a szóban forgó második kört közvetlen kapcsolatba hoztuk k-val és P-vel.
 

II. megoldás: A H1 hatszög oldalainak merőlegességét a következőképpen is igazolhatjuk. Elegendő P-nek a C'A íven felvehető helyzeteire szorítkozunk mert H1-nek nincs kitüntetett oldala, így a betűzés megváltoztatásával mindig elérhetjük az említett helyzetet. Másrészt elég az egymást Q6, Q1, Q2, Q3-ban metsző oldalakra megmutatni, hogy merőlegesek egymásra, mert H1 csúcsait fordított sorrendben betűzve (A,B,...,C' helyére rendre C',B',...,A-t írva) Q5 és Q1 valamint Q4 és Q2 felcserélődnek.
Q1 mint a PAB háromszög magasság talppontja az AB oldal A-n túli meghosszabbításán van, mert a PAB szög tompaszög, szárai között k-nak a C' és C pontokat tartalmazó, és ezért félkörnél nagyobb PB íve fekszik; hasonlóan Q2 a BC oldal B-n túli meghosszabbításának pontja. Ezekből a betűzés megfordításával kapjuk, hogy Q5, Q4 a C'B', B'A' oldalnak C'-n, B'-n túli meghosszabbításán van. Q3 viszont a CA' és Q6 a C'A szakaszon fekszik, mert a PCA', PC'A háromszögekben C-nél és A'-nél, C' és A-nál hegyes szögek vannak. Eszerint P a H2-höz viszonyítva a Q6, Q2, Q3-nál fekvő (180∘-nál kisebb) szögek terében fekszik, és a Q1-nél, Q5-nél fekvő egyik-egyik külső szög terében, ezért a Q1 szög PQ1 révén két szög különbségeként írható: Q6Q1Q2∢=PQ1Q2∢-PQ1Q6∢ a Q6, Q2, Q3-nál fekvő szögek pedig PQ6, PQ2, PQ3-mal két szög összegére bonthatók, pl. Q2Q3Q4∢=Q2Q3P∢+PQ3Q4∢.
Folytatólag a PQ1Q2B és PQ1AQ6 ,,talpponti'' húrnégyszögek, majd a PABC ,,k-beli'' húrnégyszög révén (mivel bármelyik szög egyenlő a szemben fekvő szög külső szögével) Q6Q1Q2∢=PBC∢-PAC'∢=PAC∢-PAC'=C'AC∢, és ez feltevésnél fogva derékszög: a CC' átmérő látószöge a k-n fekvő A pontból. ‐ Majdnem ugyanígy halad a bizonyítás a többi három szög esetében is. A megkezdett példát folytatva: Q2Q3Q4∢=BCP∢+PA'B'∢=BCP∢+PCB'∢=BCB'∢, ami derékszög. (Olyan, a szereplőkkel egyenlő szögekre térünk át, melyek H1 csúcsaival vannak meghatározva, majd amelyeknek csúcsuk és egyik száruk közös, és így összegük egyetlen szögként írható.)
Ezzel az állítás első részét bebizonyítottuk.
 

III. megoldás: Megmutatjuk, hogy H2-nek egy oldala a tőle számított második oldallal párhuzamos, és a harmadikra merőleges; ebből már következik, hogy a második és a harmadik oldal egymásra merőleges, vagyis az állítás első része igaz. Valóban, egyrészt pl. Q6Q1 párhuzamos Q3Q2-vel, mert egyenlő szöget alkotnak a Q6P (másképpen Q3P) félegyenessel: PQ6Q1∢=PAQ1∢=PCQ2∢=PQ3Q2∢ továbbá Q1 és Q2 a PQ3 egyenesnek ugyanazon partján feküsznek. Másrészt Q6Q1 merőleges Q3Q4-re. Ugyanis a Q6-nál derékszögű PAQ6 és a Q3-nál derékszögű A'PQ3 háromszögek hasonlók, mert P-nél fekvő hegyes szögeik PA és PA' merőlegessége folytán egymásnak pótszögei; a PAQ6 háromszög egy +90∘ szögű forgatva nyújtással áll elő A'PQ3-ból (megfelelők azok a csúcsok, amelyek a két felsorolásnak ugyanannyiadik tagjai). Ugyanez érvényes a Q1-nél, Q4-nél derékszögű PAQ1 és A'PQ4 háromszögekre is, és így a PQ6AQ1, A'Q3PQ4, négyszögekre is, mert a hasonlóság aránya mindkét esetben ugyanaz: a PA, A'P átfogók aránya. Így Q6Q1 is +90∘-os forgatva nyújtással áll elő Q3Q4-ből (ez többet is mond annál, mint amit állítottunk), ennélfogva Q3Q2 merőleges Q3Q4 -re.
 

Megjegyzés. Egyenesek párhuzamosságára támaszkodik a következő bizonyítás is. Legyen k és a PQ6 egyenes második közös pontja P*. Ekkor CQ2Q3∢=CPQ3∢=CPP*∢=CBP*∢, eszerint P*B párhuzamos Q3Q2-vel. Hasonlóan P*B'∥Q3Q4, így a Q2Q3Q4 szög egyállású a BP*B' szöggel, ez pedig derékszög.