Cím: Egyenesek mértani helye
Szerző(k):  Vigassy Lajos 
Füzet: 1960/április, 82 - 91. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Amikor mértani helyről beszélünk, rendszerint csak pontokra vonatkozó mértani helyekre gondolunk. Beszélhetünk azonban egyenesekre vonatkozó mértani helyekről is, ha az egyenest is alapelemnek tekintjük1. Ezen a pontokra vonatkozó mértani helyfogalom pontos megfelelőjét értjük: ha adva van valamely tulajdonság (követelmény), akkor az ezzel a tulajdonsággal bíró (ezt a követelményt kielégítő) egyenesek mértani helyén egyenesek olyan összességét értjük, amely egyrészt magában foglal minden, az adott tulajdonsággal bíró egyenest, másrészt minden egyenesének megvan a szóban forgó tulajdonsága.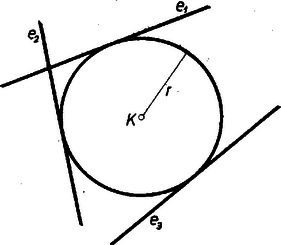
A továbbiakban egyenesek mértani helyére vonatkozó példákat mutatunk be alkalmazásokkal. Csak a síkon maradunk, térbeli mértani helyekről nem lesz szó.
1. példa. Közismert az adott K ponttól adott r távolságra levő egyenesek mértani helye (1. ábra). Ennek a követelménynek nyilván eleget tesznek a K középponttal bíró r sugarú kör összes érintői, és csak ezek.

 
 
1. ábra
 

2. példa. Ebből az is könnyen belátható, hogy egy adott r sugarú körből adott h hosszúságú húrokat kimetsző szelők mértani helye: egy az adott körrel koncentrikus másik kör érintői, ha h<2r; e kör sugarát úgy kapjuk; hogy r átfogóval és h/2 befogóval derékszögű háromszöget szerkesztünk és vesszük ennek másik befogóját, ‐ ugyanis r sugarú körben a h hosszúságú húrok ekkora távolságra vannak a középponttól. Ha pedig h=2r, akkor a keresett mértani hely az adott kör középpontján átmenő egyenesek összessége. h>2r esetén a mértani hely nem létezik, nincs a követelménynek eleget tevő egyenes.
Feladat: Adva van egy k kör, rajta kívül egy M pont és egy PQR=H háromszög. Szerkesszünk a H-hoz hasonló olyan háromszöget, amely a k-ba van beleírva, és egyik oldalának egyenese átmegy M-en.
Megoldás: Megválaszthatjuk, hogy a keresett háromszög oldalai közül pl. a QR-nek megfelelő menjen át M-en. Szerkesztünk k-ba egy a H-hoz hasonló beírt P1Q1R1=H1 háromszöget, pl. helyzetre is hasonlót: meghúzva k azon sugarait, az OP1,OQ1,OR1 félegyeneseket, amelyek párhuzamosak és egyirányúak a H köré írt kör P-hez, Q-hoz, R-hez vezető sugaraival (2. ábra).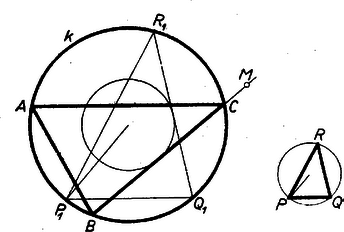
 
 
2. ábra
 

H1-et k középpontja körül forgatva a Q1R1 oldal állandóan érint egy, a k-val koncentrikus kört. Ezért a kívánt oldalegyenes gyanánt csak az M-ből e körhöz húzható két érintő felel meg. Bármelyiknek k-val való két metszéspontját kétféleképpen oszthatjuk be Ql,R1 szerepére (kivéve, ha a PQR háromszög egyenlő szárú és benne PR=PQ ebből pedig P1 helyzete a Q1,R1-nél levő szögek alapján egyértelműen meghatározható. Ezek szerint a megoldások száma 4, ill. 2. (Megoldás mindig van, mert M a k-ra nézve külső pont, a felhasznált kör pedig k belsejében fekszik.)
3. példa. Két adott A és B ponttól egyenlő távolságra fekvő egyenesek mértani helye két részből tevődik össze: egyrészt az AB egyenessel párhuzamos, másrészt az AB szakasz F felezőpontján átmenő egyenesek összességéből (3. ábra); ‐ gyakran használt elnevezéssel; az F pontra illeszkedő sugársorból, ill. az AB-vel egyirányú párhuzamos sugársorból. Az AB egyenes mindkét összességbe beletartozik.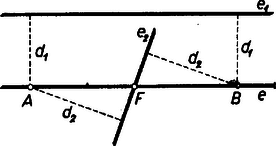
 
 
3. ábra
 

Állításunk helyessége ‐ már ami azt illeti, hogy a két összesség valamennyi tagja megfelel a követelménynek ‐ közvetlenül belátható, ill. könnyen bizonyítható. Néhány olvasóban azonban a két különböző összesség láttán felvetődik az a kétség, hátha vannak még további megfelelő egyenesek is. Bizonyítanunk kell, hogy több megfelelő egyenes nincs. Ennek során a mértani helyek felkutatására is példát látunk.
Ahogyan a két ponttól egyenlő távolságra fekvő pontok mértani helyét keresve a pontok körül egymás után több egyenlő sugárral írt körpár metszéspontjainak sorakozásából alakult ki előttünk a felező merőleges, úgy itt is célszerű több egyes eset felvételével tájékozódni. A keresett egyenesek A-tól és B-től leendő távolságának minden megválasztott d értéke mellett az egyenest csak az A ill. B körül d sugárral írt körök érintői közül választhatjuk; ezért minden közös érintőjük megfelel, és más egyenes nem. A két körnek bármely d-re van közös külső érintője, éspedig kettő. Ugyanis általában két egymástól c távolságra fekvő pont körül R, ill. r sugárral írt körnek (R≦r) akkor és csak akkor van közös külső érintője, ha egyik sem zárja magába a másikat: c+r≧R, azaz R-r≦c, és ez a feltétel itt teljesül, mert a sugarak különbsége 0. Ha d minden (pozitív) értéket felvesz, a közös külső érintők adják az AB-vel párhuzamos egyeneseket. d=0 esetén körökről már nem lehet szó (bár szokás a pontokat 0-sugarú körnek tekinteni), de enélkül is látjuk, hogy van az A- és B-től 0-távolságra fekvő egyenes: maga az AB egyenes. Továbbá 2d≦AB esetén van az A és B körüli d sugarú köröknek közös belső érintőjük, kettő, ill. egyenlőség esetén egy, mert így teljesül a közös belső érintő létezésének az előbbi jelölésekkel általában kimondott R+r≦c feltétele (hogy ti. a két kör egymáson kívül álljon). Mindezek az érintők átmennek AB felezőpontján, ezek adják az F-en átmenő sugársor egyeneseit. Ezek szerint más megfelelő egyenes valóban nincs, a bizonyítást befejeztük.
Bizonyos esetekben célszerű, ha a pont és egyenes közti távolsághoz irányítást, előjelet értünk hozzá, azt mondjuk, hogy az egyenes két oldalán fekvő pontoknak az egyenestől mért távolsága ellentétes előjelű. (Hogy melyik oldali pontok távolságát vesszük pozitívnak, ez csak megállapodás dolga; az adott helyzet egy kitüntetett szerepet játszó távolságát szokás pozitívnak venni.)
Irányított távolságokra gondolva a legutóbbi mértani helyet csak az AB-vel párhuzamos egyenesek alkotják, mert ezekhez képest A és B ugyanazon oldalon vannak, tehát a távolságok előjelben is megegyezők; viszont az F-re illeszkedő sugársor tagjaihoz képest A és B ellentétes oldalon feküsznek, az előjellel vett távolságok nem egyenlők. (E sugársorból mégis kivétel maga az AB egyenes, erre a két távolság zérus, előjel hozzáértésével sem különböző.)
4. példa. Azon egyenesek mértani helye, amelyeknek az adott A és B pontoktól mért távolságainak aránya adott m:n=k szám (k>0), ‐ ha figyelmen kívül hagyjuk a távolságok előjelét ‐ két sugársor, ezek az AB egyenesnek arra az M,N pontjára illeszkednek, amelyre MA:MB=NA:NB=k (belső ill. külső osztópont, 4. ábra).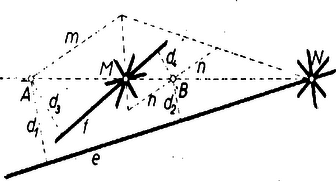
 
 
4. ábra
 

Kiveendő azonban mindkét sugársorból az AB egyenes, amelyre a két távolság 0, és így arányuk nincs értelmezve. k=1 mellett a 3. példabeli mértani helyet kapjuk. Ha k negatív, akkor a kérdésnek csak előjeles távolságok mellett van értelme. Ilyenkor csak a belső osztópontra illeszkedő sugársor a mértani hely, kifejezetten pozitív k mellett pedig csak a külső osztópontra illeszkedő sugársor, mindkétszer az AB egyenes nélkül. (Mindez az A,B körüli kd, ill. d sugarú körpár közös érintőivel a 3. példabelihez hasonló meggondolással bizonyítható, M,N valamennyi ilyen körpárnak külső, ill. belső hasonlósági pontja.) Ha a követelményt úgy fogalmazzuk, hogy az egyenesek A-tól mért távolsága a B-től mértnek k-szorosa legyen, akkor AB is beletartozik a mértani helybe.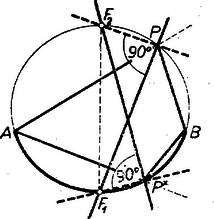
 
 
5. ábra
 

5. példa. Adott kör adott ívén ‐ pl. az 5. ábrán az A,B pontokkal meghatározott ívek közül az AF1B íven ‐ nyugvó kerületi szögek szögfelezőinek mértani helye az ív F1 felezőpontjára illeszkedő sugársornak egy része: azok az egyenesek, amelyeknek egyik félegyenese a BF1A szög terében fekszik, e szög szárait nem beleértve. Ismeretes ugyanis, hogy az AF1B íven nyugvó kerületi szögek felezői az ívet is felezik, átmennek az F1 felezőponton; és fordítva az F1-en átmenő sugársor mondott részét képező minden egyes f egyenes a kört másodszor az AF2B ív valamely belső pontjában metszi, ez a csúcsa annak a kerületi szögnek, amelynek felezője f. (Hasonlóan látható be, hogy a kimaradt egyenesek a ,,másik'' AB íven, a kiegészítő AF2B íven nyugvó kerületi szögek mellékszögeit felezik ‐ kivéve ismét F1A-t és F1B-t. Ugyanígy az F1-gyel átellenes F2 pontra illeszkedő sugársor egyeneseinek egy része az AF1B íven nyugvó kerületi szögek mellékszögét felezi, a többiek pedig az AF2B íven nyugvó kerületi szögeket.)
Feladat: Adva van egy kör és rajta két pont: A és B, amelyek nem egy átmérő végpontjai. Tűzzük ki a kisebb AB íven a C pontot úgy, hogy a CA és CB húrok aránya adott m:n=q érték legyen.
Megoldás: Ismeretes, hogy a háromszög bármelyik szögének felezője olyan két részre osztja a szemben fekvő oldalt, amelyeknek aránya megegyezik a szöget bezáró oldalak arányával. Ha már most F a nagyobb AB ív felezőpontja, és D az AB szakaszt az előírt arányban osztó pont, akkor a keresett C pontot az FD egyenes metszi ki a körből (6. ábra; itt előjel kérdésről nem lehet szó, mert a húrok nem párhuzamosak).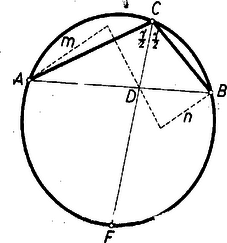
 
 
6. ábra
 

A következő 6. és 7. példában az előjellel vett távolságok kérdését majd együtt vizsgáljuk, mert a kérdések ebből a szempontból egymásba mennek át.
6. példa. Keressük azon egyenesek mértani helyét, amelyeknek az adott A és B pontoktól mért távolságainak összege adott szakasszal egyenlő: d1+d2=2s.
A keresett egyenesek összességét az A körül d1=x és B körül d2=2s-x sugárral írt körpár közös érintői adják, ha x felvesz minden 2s-nél nem nagyobb, nem negatív értéket, ezekkel ugyanis 2s-x sem negatív. (Az x=0, ill. 2s-x=0 sugarú körön az A, ill. B pontot értjük; ha egyik kör sugara 0, akkor a körpár közös külső és közös belső érintői páronként azonosak.) Kívánatos azonban, hogy a mértani helyet áttekinthetőbben jellemezzük.
a) Közös külső érintőik mindenesetre vannak a körpároknak, vagyis amelyekhez képest A és B ugyanazon oldalon vannak, mert teljesül létezésüknek fent kimondott feltétele, hiszen pl. x=s mellett a két sugár különbsége 0. Legyen egy körpár egy közös külső érintője e1 erre tehát 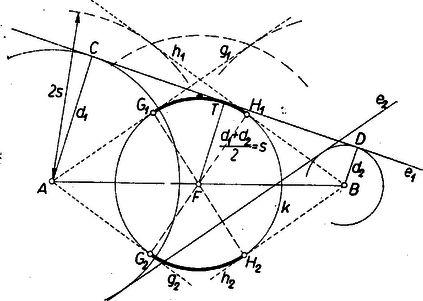AC+BD=2s (7. ábra).
 
 
7. ábra
 

Az ABDC négyszög derékszögű trapéz, az AB és CD szárak F és T felezőpontjaival határolt középvonalra FT=(AC+BD)/2=s, továbbá FT merőleges e1-re, eszerint e1 (T-ben) érinti az AB szakasz F felezőpontja körül s sugárral írt k kört. Eszerint a keresett mértani helybe a minden körpárra közös k mindazon érintői beletartoznak, amelyeknek ugyanazon oldalán fekszik A és B. Ha 2s≧c(=AB), vagyis A és B a k-ra nézve nem külső pontok, akkor k minden érintője a mértani helyhez tartozik, 2s<c mellett pedig csupán azok, amelyek k-t a sem A-ból, sem B-ből ,,nem látható'' G1H1, G2H2 ívein érintik, hozzáértve az ívek végpontjaihoz tartozó, vagyis az A-n, B-n átmenő érintőket.
b) Közös belső érintői ellenben nem mindig vannak az A körül x és B körül 2s-x sugárral írt körpárnak ‐ vagyis olyanok, amelyekhez képest A és B az ellentétes oldalakon fekszenek ‐, hanem csak akkor, ha x+(2s-x)=2s≦c. Ha ez a feltétel teljesül, a közös belső érintőknek a körzsugorítás módszerével végzett szerkesztésére gondolva 2s<c esetére nyilvánvaló, hogy míg x minden fenti értékén végigfut, addig a közös belső érintők két párhuzamos egyenesnyalábot alkotnak. Irányukat az x=0, ill. x=2s értékhez tartozó ,,körpárok'' felhasználásával úgy kapjuk, hogy az AB=c átfogó fölé (egyik oldalán) 2s-sel mint befogóval derékszögű háromszögeket szerkesztünk (általában kettőt lehet, kivételesen egyet) és vesszük ezek másik befogóinak irányát (a kivételes esetben mindkét befogó irányát). A két irány párhuzamos az előbbi kör G2H1,G1H2 átmérőivel. Egy-egy nyalábba, mint a keresett mértani hely részébe mindazok az egyenesek tartoznak bele, amelyek metszik az AB szakaszt, az A-n, B-n átmenő párhuzamost is beleértve. Vagyis a k-hoz G1 és H2-ben, ill. G2 és H1-ben húzott érintőkkel határolt síksávnak a sáv határaival párhuzamos egyeneseiről van szó (7. ábra, e2).
2s=c esetére megállapításaink kissé módosulnak: minden körpárnak csak egy közös érintője van és az merőleges AB-re, a két egyenesnyaláb azonossá válik, a mértani hely második részét az AB szakaszt merőlegesen metsző egyenesek nyalábja adja.
Összefoglalva: 2s és c bármely nagyságviszonya esetén vannak a követelménynek megfelelő egyenesek, vagyis a mértani hely létezik. A mértani helyet 2s>c esetén az AB szakasz F felezőpontja körül s sugárral írt kör valamennyi érintője alkotja; A és B valamennyinek ugyanazon oldalán fekszik.
2s=c esetén ugyanezen érintők és az AB szakaszt merőlegesen metsző egyenesek nyalábja a mértani hely. Az AB-re A-ban és B-ben állított a,b merőlegeseket leszámítva A és B az érintőknek ugyanazon oldalán, a nyaláb egyeneseinek pedig ellentétes oldalán feküsznek. Végül
2s<c esetén az említett kör fent leírt íveihez tartozó érintők és a két fent leírt módon szerkeszthető, párhuzamos egyenesnyaláb alkotja a mértani helyet, A és B-nek az egyenesekhez képest elfoglalt helyzete ugyanaz, mint a 2s=c esetben.
7. példa. Keressük azon egyenesek mértani helyét, amelyeknek az adott A és B pontoktól mért távolságainak különbsége adott 2s szakasszal egyenlő: d1-d2=2s. A különbségben hangsúlyozzuk A és B sorrendjét, vagyis csak azokat az e egyeneseket fogadjuk el, amelyekre az Ae=d1 távolság 2s-sel nagyobb a Be=d2 távolságnál.
A keresett összességet a B körül d2=x, és az A körül d1=x+2s sugárral írt körpár közös érintői adják, ha x felvesz minden nem negatív értéket. Itt is törekszünk az áttekinthetőbb leírásra.
a) Kezdjük most a vizsgálatot a közös belső érintőkkel. Ilyenek létezésének szükséges és elegendő feltétele, hogy (x+2s)+x=2x+2s≦c legyen; ebből x≦(c-2s)/2, vagyis x≧0 folytán a feltétel így írható: 2s≦c. Tegyük fel, hogy ez teljesül és legyen 2s<c esetére egy ilyen típusú körpár egyik közös belső érintője e1 vagyis erre 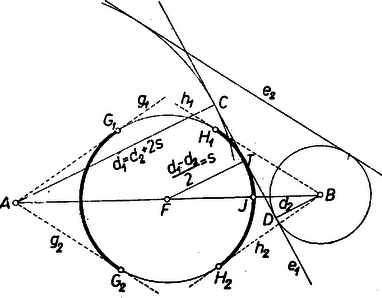AC-BD=2s (8. ábra).
 
 
8. ábra
 

Az ACBD négyszög trapéz, benne az AB és CD átlók F és T felezőpontjai közti szakaszra FT=(AC-BD)/2=s, továbbá FT merőleges e1-re, eszerint e1 (T-ben) érinti az. AB szakasz F felezőpontja körül s sugárral írt k kört. Feltétel szerint A és B a k-ra nézve külső pontok.
A B körüli ,,kör'' x=0 esetén, még csak egy pont, így a B-ből k-hoz húzható h1,h2 érintőket kapjuk, legyenek érintési pontjaik H1,H2; x fenti legnagyobb értékével pedig a körpár tagjai érintkeznek, az egyetlen közös belső érintő k-t az AB-vel való, B-hez közelebbi J metszéspontjában, a rövidebb H1H2 ív felezőpontjában érinti, és a közbülső x értékek mellett az érintési pontok egyike a H1J, másika a H2J íven van, mert a körpár belső hasonlósági pontjának B-től A felé mért cx/(2x+2s)=c:(2+2s/x) távolsága x növekedésével növekszik (2+2s/x csökken, ezért a hányados növekszik), a pont B-től J-ig eltolódik. Eszerint a mértani hely idevágó részét a k-t a H1H2 íven érintő egyenesek alkotják.
2s=c esetén x egyetlen lehetséges értéke x=0, és k átmegy B-n, a mértani hely idevágó része egyedül a k-hoz B-ben húzott, AB-re merőleges b érintőből áll.
b) Közös külső érintőjük sem mindig van körpárunk tagjainak, csak akkor ha (x+2s)-x=2s≦c, vagyis a feltétel azonos az előbbivel. Ha ez teljesül, akkor a közös külső érintőknek a körzsugorítás módszerével végzett szerkesztésére gondolva, 2s<c esetére nyilvánvaló, hogy míg x minden fenti értéken végigfut, addig minden közös külső érintő párhuzamos két iránnyal, az A körül 2s sugárral írt körhöz B-ből (vagy ami ugyanaz: k-hoz B-ből) húzható h1,h2 érintők irányával. Helyzetüket tekintve pedig e közös érintők kitöltik a h1-gyel, ill. h2-vel kettévágott síknak azt a félsíkját, amely nem tartalmazza az A pontot. h1 és h2 hozzátartozik a mértani helyhez.
2s=c esetén a két félsík azonos, az egyenesek merőlegesek AB-re és azt az AB szakasz B-n túli meghosszabbításán, ill. B-ben metszik.
Összefoglalva: a kérdéses mértani hely csak 2s≦c esetére létezik,
2s<c esetére k fent leírt H1H2 ívének érintőiből és a két félsík h1-gyel, h2-vel párhuzamos egyeneseiből áll; A és B az érintőknek ellentétes oldalán, a félsík egyeneseinek ugyanazon oldalán feküsznek.
2s=c esetére pedig az AB-re B-ben állított b merőleges által kettévágott sík A-t nem tartalmazó félsíkjának b-vel párhuzamos egyenesei adják a mértani helyet, beleértve b-t is.
Most már a Be-Ae=2s tulajdonságú egyenesek mértani helyét természetesen a fentinek az AB szakasz felező merőlegesére való tükrözésével kapjuk, vagyis ez a G1G2 ív érintőiből és a g1,g2-vel kettévágott sík B-t nem tartalmazó félsíkjának g1, ill. g2-vel párhuzamos egyeneseiből áll, 2s=c esetén pedig az AB-re A-ban állított a merőleges által kettévágott sík B-t nem tartalmazó félsíkjának a-val párhuzamos egyeneseiből, beleértve a-t is.
Ha 2s=0, akkor a 3. példabeli kérdéshez jutunk. Ekkor a k kör az F pontra zsugorodik össze, a k-t a B-ből látható H1H2 íven érintő egyenesek összessége helyett az F-re illeszkedő sugársor adódik, másrészt a h1,h2 érintők mindegyike azonossá válik az AB egyenessel, így a két félsík párhuzamos egyenesei helyett a sík valamennyi az AB-vel párhuzamos egyenese áll előttünk.
A 6‐7. példákat összevonhatjuk, mert a 7. példában kapott mértani hely mintegy folytatása a 6. példabelinek. Eredményeinket átcsoportosítva látjuk, hogy a k kör e érintőire nézve az A és B-től mért, és közönségesen, előjel nélkül értett távolságokból a 2s állandót 2s<c esetén akkor kapjuk összeadással, ha a pontok e-nek ugyanazon oldalán feküsznek, és akkor kapjuk (alkalmas sorrendben vett kivonással, ha pontjaink e-nek ellentétes oldalain feküsznek (9. ábra); 2s=c esetén viszont mindig összeadással.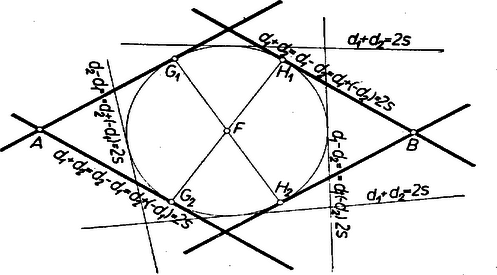
 
 
9. ábra
 

Az utóbbi típusú helyzetekben van értelme annak, hogy a távolságokat előjellel lássuk el, így pedig különbségük előjellel vett összegnek tekintendő: d1-d2=d1+(-d2), d2-d1=d2+(-d1). És hasonlóan a kitüntetett g és h érintőkkel párhuzamos p egyenesekre nézve az A és B-től mért távolságokból a 2s állandó, akkor adódik kivonással, ill. összeadással, ha pontjaink ugyanegy, ill. ellentétes oldalán feküsznek p-nek (10. ábra, ugyanilyen a 2s=c eset megfelelő ábrája is).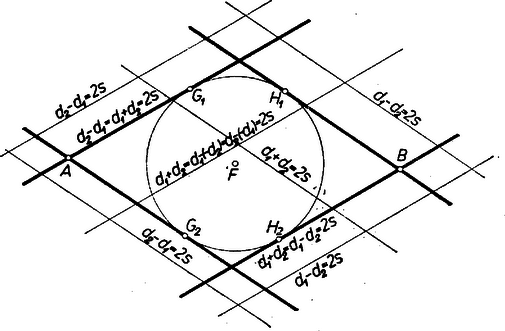
 
 
10. ábra
 

Az utóbbi típusú helyzetekben az összeget kétféleképpen is tekinthetjük előjellel megkülönböztetett távolságok alkalmas sorrendben vett különbségének: d1+d2=d1-(-d2)=d2-(-d1).
Eszerint ‐ ha a távolságokat az egyenesek két oldalán ellentétes előjellel, éspedig a nagyobb abszolút értékű távolság oldalán pozitívnak vesszük, akkor azon egyenesek mértani helye, amelyeknek az adott A és B pontoktól mért távolságaival összege adott 2s szakasszal egyenlő: az AB szakasz felezőpontja körül s sugárral leírt kör valamennyi érintője. Ez a mértani hely 2s és az AB szakasz bármely nagyságviszonya mellett létezik. ‐ Azon egyenesek mértani helye pedig, amelyekre az A és B pontoktól mért és az előzők szerint előjellel ellátott távolságok különbsége adott 2s szakasszal egyenlő: mindazon egyenesek összessége, amelyek párhuzamosak az AB szakasz felezőpontja körül s sugárral írt körhöz A-n (és B-n) át húzott érintőkkel. (Ha az adott 2s szakasz nagyobb A és B távolságánál, akkor ez a mértani hely nem létezik.) ‐ Az utóbbi eredményt úgy is kimondhatjuk, hogy a mértani helyet arra a két irányra merőleges egyenesek adják, amelyre a két pont távolságának vetülete az adott 2s-sel egyenlő. (Ezért nem létezik a mértani hely a 2s>AB nagyságviszony esetére. ) ‐Érdemes még a két példa eredményét összehasonlítva úgy is kimondani: előírt távolságösszeg esetén az egyeneseknek egy ponttól való távolsága állandó, előírt különbség esetén pedig az iránya.
 

Feladat: Adva van négy pont: P, O, A, B. Szerkesztendő P-n át olyan egyenes, amely O-tól akkora távolságra van, mint A-tól és B-től együttvéve.
Megoldás: Legyen az AB szakasz felezőpontja O1. A keresett egyenes a 6. példa szerint O1-től feleakkora távolságra van, mint A-tól és B-től együttvéve, vagyis amennyire O-tól kell lennie; így O1-től és O-tól mért távolságainak aránya 1:2. Ezek szerint a 4. példa alapján más egyenesekről nem lehet szó, mint amelyek az OO1 szakasz 1:2 arányú M belső, ill. N külső osztópontját P-vel összekötik (11. ábra).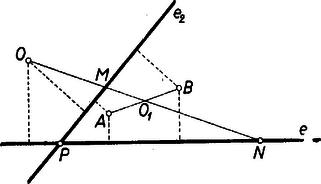
 
 
11. ábra
 

A PN=e1 egyenesre a követelmény ‐ legalábbis előjellel ‐ mindig teljesül, mert e1 O-t és O1-et nem választja szét, és így az Oe1=2⋅O1e1 egyenlőség mindig fennáll, a 2⋅O1e1=Ae1+Be1, egyenlőség pedig esetleg csupán előjelekkel, ha ti. e1 az A-t elválasztja B-től. A PM=e2 egyenes viszont csak akkor megoldás, ha nem választja el A-t B-től; ugyanis m szétválasztja O-t és O1-et, ezért az Oe2=2⋅O1e2 egyenlőség csak abszolút értékben, az előjelek mellőzésével áll fenn, így pedig az Ae2+Be2=2⋅O1e2 egyenlőséget sem érthetjük előjellel, szétválasztás esetére sem.
(A 3. példa után úgy látszott, hogy a távolságoknak előjellel való vétele ,,erősebb'' követelmény, kevesebb megoldást enged meg; itt viszont e1-et szétválasztás esetében éppen csak az előjel figyelembe vételével tudtuk elfogadhatóvá tenni. Ez a látszólagos ellentétesség megoldásunk kulcslépésén múlik, azon ti., hogy az Ae1+Be1 összeget a trapéz-középvonal módszerrel képeztük, és ez csak akkor érvényes, ha e1 nem választja el A-t B-től. ‐ A szerkesztésünk megoldását kívánó gyakorlati cél viszont azt is előírhatja, hogy A és B-nek a keresett e egyenestől mért távolságai akkor is előjel nélkül értendők, ha e elválasztja A-t és B-t.)*
Utolsó példánkban egy a jelenlegi középiskolai anyagban nem szereplő, de könnyen megérthető fogalmat is felhasználunk: két kör ún. hatványvonalát, valamint néhány erre vonatkozó tételt. Ezeket csak kimondjuk és bizonyításukat az olvasóra bízzuk. Két (nem közös középpontú) kör hatványvonalán szemléletesen a sík azon P pontjainak összességét értjük, amelyekből a körökhöz húzható érintőknek P-től az érintési pontig terjedő szakaszai egyenlők. A hatványvonal a körök középpontjait összekötő egyenesre merőleges egyenes. Ha a körök metszik, vagy érintik egymást, akkor hatványvonaluk átmegy metszéspontjaikon, érintkezési pontjukon. Ha pedig nincs közös pontjuk, akkor hatványvonalukat megszerkeszthetjük egy mindkettőjüket metsző, tetszés szerinti harmadik kör felhasználásával a következő tétel alapján: három kör páronként vett hatványvonalai, ha a középpontok nem esnek egy egyenesbe, egymást egy pontban, a három kör ún. hatványpontjában metszik. Ha a körök metszik egymást, akkor, bár közös húrjuk belső pontjaiból nem lehet a körökhöz érintőt húzni, azért ezeket sem zárjuk. ki a mértani helyből. Ezt megindokolhatjuk azzal, hogy a hatványvonal egy más, nem szemléletes meghatározásának ezek a pontok is megfelelnek. Ez a meghatározás a következő: ha a körök középpontjai O1,O2, sugaraik r1,r2, akkor hatványvonalukat azok és csak azok a P pontok alkotják, amelyekre teljesül a PO12-r12=PO22-r22 egyenlőség. Látható, hogy ha lehet a körökhöz P-ből érintőket húzni, akkor az egyenlőség azt fejezi ki, hogy az érintőszakaszok négyzetei egyenlők.
8. példa. Adva van egy k kör és két pont: A és B. Mi azoknak az egyeneseknek a mértani helye, amelyek összekötik k és az adott pontokon átmenő, k-t metsző körök közös pontjait?
Az előrebocsátottak szerint az összekötő egyenes egyben hatványvonala is a metszéspontokat megadó körpárnak. Ha azonban kérdésünket így fogalmaznók: mi a mértani helye az A, B-n átmenő körök és k hatványvonalának, ezzel a követelményt megváltoztatnók, tágítanók, mert már láttuk, hogy két körnek ‐ ha középpontjaik különbözők, ‐ hatványvonaluk mindig van, közös szelőjük pedig csak akkor, ha van közös pontjuk; sőt szigorúan véve akkor sincs, ha érintkeznek, vagyis csak egy közös pontjuk van.
Legyen két az A, B-n átmenő és k-t metsző kör c1, c2, k-val való metszéspontjaik C1, C'1, ill. C2, C'2, ekkor a keresett mértani hely két tagja C1C'1 és C2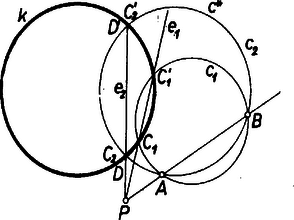C'2 (12. ábra).
 
 
12. ábra
 

Az előbbi a k, c1 körpár, az utóbbi a k, c2 körpár hatványvonala, ezért egymást az előrebocsátott tétel szerint a c1, c2 körpár hatványvonalán, az AB egyenesen metszik (feltéve, hogy AB felező merőlegese nem megy át k középpontján), legyen ez a pont P. A tétel szerint bármely a k-t metsző és A-n, B-n átmenő körnek k-val közös szelője is átmegy P-n, ennélfogva a keresett mértani hely a P-re illeszkedő sugársornak része. Ugyanis c1-et állandóan tartva, a c2 helyett pedig minden más szóbajövő (c1-től különböző) c kört sorravéve a k, c1, c körhármas hatványpontja P, mert a k, c1 körpár hatványvonala állandóan a C1C'1 a c1, c körpáré állandóan az AB egyenes, ezeknek egyetlen közös pontja P, ezért rajta a k, c körpár hatványvonala is átmegy.
Várható az eddigiekből, hogy ha P a k-belsejében vagy magán k-n adódik, akkor a keresett mértani hely a P-re illeszkedő sugársor, ha pedig P kívül van k-n, akkor a sugársor mindazon egyenesei alkotják a mértani helyet, amelyek metszik k-t (ill. legalább érintik). Ennek helyes voltát az utóbbi esetre mutatjuk meg, belső P esetére a bizonyítást hasonlóan elvégezheti az olvasó. Mivel P kívül van k-n, azért C1C'1-nek a meghosszabbításában fekszik, c1-en is kívül van, tehát nincs az AB szakaszon; feltesszük, hogy a betűzés olyan, amelyre PA<PB. Legyen egy a P-n átmenő, k-t metsző egyenes e2, k-val való két metszéspontja D, D' azt kell megmutatnunk, hogy van olyan az A-n, B-n átmenő kör, amely átmegy a D, D' pontokon. Tekintsük az A,D,D' pontokkal meghatározott c* kört (az ábrán D≡C2, D'≡C'2), legyen ennek AB-vel való második közös pontja B*. Így azt kell belátnunk, hogy B*≡B-e2 és PA a c*-nak szelői, ezért a PA⋅PB* szorzat egyenlő PD⋅PD'-vel, mert ismert tétel szerint mindkettő egyenlő a P-ből c*-hoz húzható érintőszakasz négyzetével. e2 a k-nak is szelője, ezért hasonló indokolással az utóbbi szorzat egyenlő PC1⋅PC'1-vel. Végül, PC1 k-nak és c1-nek szelője, ezért az utóbbi szorzat egyenlő PA⋅PB-vel, vagyis PA⋅PB*=PA⋅PB, ebből PB*=PB, és B*≡B, amit bizonyítani akartunk.
A teljes diszkussziót az olvasóra bízzuk, megjegyezve, hogy a mértani hely párhuzamos egyenesnyalábbá is elfajulhat. ‐ Egyébként az A,B pontokon átmenő körök összessége egy ,,körökre vonatkozó mértani hely'', egy típusa az ún. körsoroknak. Megállapításaink a mértani hely fogalmát nem használó tételként is kimondhatók: egy adott körnek és két adott ponton átmenő bármelyik körnek a hatványvonala egy állandó ponton megy át.
Feladat: Adva van egy k kör, két pont: A,B és egy h szakasz. Szerkesszünk a két ponton átmenő olyan c kört, amely k-ból h hosszúságú húrt metsz ki.
Megoldás: k-nak h hosszúságú húrjai egy a k-val koncentrikus k1 kört érintenek (2. példa), ezért megszerkesztjük egyrészt k1-et, másrészt a 8. példa szerint az A,B-vel meghatározott körsor és k közös P hatványpontját (13. ábra).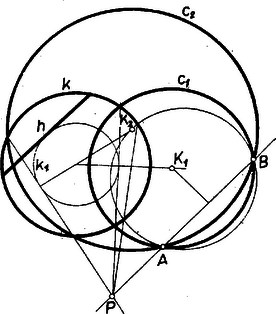
 
 
13. ábra
 

Most már a P-ből k1-hez húzott érintők metszik ki k-ból a keresett kör további két pontját.
A bemutatott feladatok megoldásából látható, hogy szerkesztésekben az egyenesekre vonatkozó mértani helyeket a pontokra vonatkozó mértani helyekhez hasonlóan eredményesen használhatjuk fel.
Irodalom: J. Petersen: Méthodes et théories pour la résolution des problémes de constructions géométriques.
1 A 911. feladat is egyenesek mértani helyére vonatkozott (XVIII, kötet 3, szám, 1959. március).

*Erre a kérdésre még visszatérünk.