Kezdőlap


Cím:	A bolygómozgás területi elvének egyszerű levezetése
Szerző(k):	Bodócs István
Füzet:	1959/november, 154. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A TERÜLETI SEBESSÉG ÁLLANDÓSÁGA. A centrális mozgásokat az jellemzi, hogy a vezérsugár egyenlő idők alatt egyenlő területeket ír le a térben, s ez a ,,területi elv'' mértani okok miatt minden centrális mozgásra érvényes, mégpedig az erőtörvény alakjától függetlenül!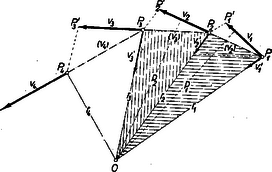

Levezetés céljából induljunk ki abból a pillanatból, amikor az ábra szerint a bolygó tömegközéppontja (a következőkben: a mozgó pont) a vonzó

O

középponttól

r_{1}

távolságra levő

P_{1}

helyre érkezik

v_{1}

sebességgel. Ha nem volna vonzó erő, akkor tehetetlensége következtében 1 mp múlva a

P'_{1}

helyzetbe jutna, a vonzás miatt azonban ugyanezen idő alatt bizonyos

v'_{1}

elmozdulás jön létre a centrum irányában, s így az első mp végére

P_{2}

-be jut az eredményvonallal jelzett eredő

v_{2}

sebességgel, s eközben az

r_{1}

vezérsugár a vízszintes árnyékolású területet írja le.
Ha nem lenne vonzás, akkor a

P_{2}

helyre érkezett pont megváltozott,

v_{2}

sebességgel 1 mp múlva a

P'_{2}

helyre kerülne, miközben azonban

v'_{2}

sebességet nyer a centrum felé, s ennek következtében a második mp végére az eredő sebesség

v_{3}

, a pont helyzete

P_{3}

, a vezérsugár leírta terület pedig a függőleges árnyékolású háromszög lesz. Ezt az eljárást folytatva: a harmadik mp végén az eredő sebesség

(v_{4})

, a mozgó pont helyzete

P_{4}

, a vezérsugár leírta terület pedig az árnyékolatlan

r_{3} r_{4} (v_{4})

háromszög lesz. A szerkesztésből mármost világosan láthatók a következők
1. Mindegyik vezérsugár súlyvonala egy balról nyitott

O P_{1} P'_{2}

, illetve

O P_{2} P'_{3}

nagyobb háromszögnek, amelynek jobboldali zárt fele az előző mp-ben leírt területet, a vele egyenlő területű nyitott fele pedig a következő mp-hez való átmenetet képviseli.
2. Mivel az eredő sebességet paralelogramma-szerkesztéssel nyerjük, ennélfogva az egyes vezérsugarakhoz tartozó nyitott és zárt háromszögek egyenlő területűek, mert alapjuk közös, magasságuk pedig a párhuzamos eltolás közben nem változik s így a nyitott

▵

-ek a következő mp-ben leírt területbe mennek át. E

▵

-eknek tehát csak az alakjuk különböző, területük azonban ugyanakkora.
Ha tehát most a

v_{1}

, illetve

v_{2}

sebességeket tekintjük alapnak, s a vonzó centrumból rájuk húzott merőlegeseket (a latin ,,perpendikuláris'' szó kezdőbetűjéről)

p_{1}

, illetve

p_{2}

-vel jelöljük, akkor az említett

▵

-ek területének egyenlősége miatt

\begin{matrix} p_{1} v_{1} = p_{2} v_{2}, \end{matrix}

vagy aránylat alakjában írva

\begin{matrix} v_{1} : v_{2} = p_{2} : p_{1}, \end{matrix}

tehát a mindenkori sebességek fordítva aránylanak a vonzó központból rájuk húzott merőlegesekhez.
A bolygó tehát a Napközelben éri el, legnagyobb

v_{0}

sebességét, amikoris a hozzá tartozó merőleges éppen a legrövidebb vezérsugár:

r_{0} = a - c

, a legkisebb

v_{a}

sebesség viszont a naptávolnál (aphelium) jelentkezik, amikor a hozzá tartozó merőleges a leghosszabb vezérsugár:

r_{a} = a + c \cdot A

kettő hányadosa, azaz

\begin{matrix} \frac{v_{0}}{v_{a}} = \frac{napközeli sebesség}{naptávoli sebesség} = \frac{a + c}{a - c}, \end{matrix}

hol az ellipszis fél nagytengelye

a

, lineáris excentricitása pedig

c

. Ezzel azután előkészítettük az utat a sebesség szélső értékeinek tényleges meghatározásához.

II. A SEBESSÉG SZÉLSŐ ÉRTÉKEI a területi- és az energia-elv segítségével határozhatók meg. Az utóbbi szerint a mozgási és helyzeti energia összege az egész mozgás folyamán állandó marad, vagyis

\begin{matrix} \frac{m v_{0}^{2}}{2} - \frac{k M m}{r_{0}} = \frac{m v_{a}^{2}}{2} - \frac{k M m}{r_{a}} \end{matrix}

(1)

ahol

k

a tömegvonzás állandója,

M

a Nap,

m

pedig a bolygó tömege, a helyzeti energiát pedig azért vesszük

-

előjellel számításba, mert növekvő

r

esetén értéke csökken.
A területi elv szerint viszont

\begin{matrix} v_{a} r_{a} = v_{0} r_{0}, \end{matrix}

(2)

s így két egyenletünk van a két ismeretlen sebesség meghatározására. A második négyzetéből

\begin{matrix} v_{a}^{2} = v_{0}^{2} \cdot \frac{r_{0}^{2}}{r_{a}^{2}} \end{matrix}

(

2'

)

s ezt (1)-be helyettesítve,

v_{0}^{2}

-re mindjárt rendezve és kiemelve

\begin{matrix} v_{0}^{2} (1 - \frac{r_{0}^{2}}{r_{a}^{2}}) = 2 k M (\frac{1}{r_{0}} - \frac{1}{r_{a}}) . \end{matrix}

Közös nevezőre hozva

\begin{matrix} v_{0}^{2} (\frac{r_{a}^{2} - r_{0}^{2}}{r_{a}^{2}}) = \frac{2 k M}{r_{0}} (\frac{r_{a} - r_{0}}{r_{a}}), \end{matrix}

majd a zárójeles részeket a jobb oldalival egyszerűsítve

\begin{matrix} v_{0}^{2} \frac{r_{a} + r_{0}}{r_{a}} = \frac{2 k M}{r_{0}} \end{matrix}

s ebből a keresett

\begin{matrix} v_{0}^{2} = 2 k M \frac{r_{a}}{r_{0} (r_{a} + r_{0})} . \end{matrix}

Mivel az ellipszis adataival kifejezve

\begin{matrix} r_{a} = a + c r_{0} = a - c \end{matrix}

ezeket helyettesítve

\begin{matrix} v_{0}^{2} = \frac{k M}{a} \cdot \frac{a + c}{a - c} \end{matrix}

(3)

alakban nyerjük a napközelben jelentkező sebesség négyzetét, amiből maga a sebesség egyszerű négyzetgyökvonással nyerhető.
A (3) értékét (

2'

)-be helyettesítve: egyszerűsítés után a naptávolhoz tartozó sebességre vonatkozólag

\begin{matrix} v_{a}^{2} = \frac{k M}{a} \cdot \frac{a - c}{a + c} . \end{matrix}

Ezzel azután előkészítettük az utat a tetszés szerinti

r

vezérsugárhoz tartozó

v

sebesség meghatározására!

III. A SEBESSÉG ÁLTALÁNOS KIFEJEZÉSE szintén az energia-elv alapján történik a

v_{0}

perihélium-sebesség felhasználásával az előbbihez hasonló lépésekben:

\begin{matrix} \frac{m v^{2}}{2} - \frac{k M m}{r} = \frac{m v_{0}^{2}}{2} - \frac{k M m}{r_{0}} \\ v^{2} - \frac{2 k M}{r} = v_{0}^{2} - \frac{2 k M}{r_{0}} . \end{matrix}

Helyettesítve

v_{0}^{2}

-nek (3) alatti kifejezését és

v^{2}

-re rendezve, majd

2 k M

kiemelése után közös nevezőre hozva

\begin{matrix} v^{2} = \frac{k M}{a} \cdot \frac{a + c}{a - c} + 2 k M (\frac{r_{0} - r}{r_{0} r}) . \end{matrix}

Helyettesítve

r_{0} = a - c

értéket, majd

k M

kiemelése után közös nevezőre hozva

\begin{matrix} v^{2} = k M [\frac{a + c}{a (a - c)} + 2 \frac{a - c - r}{(a - c) r}] = k M \frac{a r + c r + 2 a^{2} - 2 a c - 2 a r}{a (a - c) r} . \end{matrix}

A számláló harmadik és negyedik tagját

2 a

kiemelése után előre hozva, s a lehetséges összevonások után a közös

r

tényezőt ‐ jellel kiemelve

\begin{matrix} v^{2} = k M \frac{2 a (a - c) - r (a - c)}{a (a - c) r}, \end{matrix}

majd a törtet két tagra bontva, a lehetséges egyszerűsítések elvégzése után végleges

\begin{matrix} v^{2} = k M (\frac{2}{r} - \frac{1}{a}) \end{matrix}

(4)

aránylag egyszerű alakban nyerjük a bolygómozgás sebességének általános képletét.

IV. ALKALMAZÁS A MESTERSÉGES BOLYGÓK PROBLÉMÁIRA.
1. A körsebesség akkor szerepel, amikor a vezérsugár

r = a

állandó. Ekkor a (4) képlet zárójeles részének értéke

2 / r - 1 / r = 1 / r

lesz s így a körsebesség

\begin{matrix} v = \sqrt[]{\frac{k M}{r}} \end{matrix}

(5)

alakban állítható elő, hol

r

a körpálya sugarát jelenti. Ha tehát a vonzó centrumtól

r

távolságban s rá merőlegesen kilövünk egy testet az (5) sebességgel, akkor ellenállásmentes térben körpályán fog keringeni. Egy teljes

T

keringési idő alatt a

v

sebességgel megtett út

2 r π

lesz, s így a

T v = 2 r π

összefűggésből (Kepler III. törvényének megfelelően!)

\begin{matrix} T = \frac{2 r π}{v} = \frac{2 r π}{\sqrt[]{k M}} \cdot \sqrt[]{r} = 2 π \sqrt[]{\frac{r^{3}}{k M}} \end{matrix}

(6)

Ezt a kifejezést igen érdekes alakra hozhatjuk annak megfontolásával, hogy a tömegegységre ható

\frac{k M}{r^{2}}

erő tulajdonképpen az

r

távolságban jelentkező

g

gravitációs gyorsulást jelenti, ha tehát a (6) kifejezésben szereplő tört számlálóját és nevezőjét egyaránt osztjuk

r^{2}

-tel, akkor a teljes

T

periódus új kifejezése

\begin{matrix} T = 2 π \sqrt[]{\frac{r}{g}} \end{matrix}

oly ideális inga teljes lengésidejével egyenlő, melynek hosszúsága a vonzó centrumtól számított

r

távolság,

g

pedig a kérdéses helyen uralkodó gyorsulás.
Egyébként a körsebesség egészen elemi úton is levezethető annak belátásával, hogy a körmozgás fenntartásához szükséges

m v^{2} / r

centripetális erőt tulajdonképpen az

m

tömegnek

m g

súlya képviseli s így az

\begin{matrix} \frac{m v^{2}}{r} = m g \end{matrix}

feltételi egyenletből

v^{2} = r g

, illetve

\begin{matrix} v = \sqrt[]{r g} . \end{matrix}

(7)

Egyébként az (5) képlet is ugyanerre az alakra hozható, mert a gyökös rész számlálóját és nevezőjét

r

-rel szorozva

\begin{matrix} v = \sqrt[]{r \cdot \frac{k M}{r^{2}}}, \end{matrix}

már pedig előző meggondolásaink szerint a gyök alatti tört éppen a

g

gyorsulást jelenti, mely itt általánosabb értelemben veendő.
Mivel Newton törvénye értelmében a nehézségi erő terében jelentkező gyorsulások fordítva arányosak a vonzó központtól számított távolság négyzetével, ennélfogva a Föld sugarát

R

, a felszíni gyorsulást pedig

G

betűvel jelölve (mert ott a legnagyobb!) a

\begin{matrix} \frac{g}{G} = \frac{R^{2}}{r^{2}} \end{matrix}

összefüggésből nyert

\begin{matrix} g = G \frac{R^{2}}{r^{2}} \end{matrix}

értéket (7)-be helyettesítve

\begin{matrix} v = \sqrt[]{r \cdot \frac{R^{2}}{r^{2}} \cdot G} = \sqrt[]{\frac{G R^{2}}{r}} \end{matrix}

alakban nyerjük a körsebességet egy tetszésszerinti

r

távolságra nézve. Ha ezt egyszerűség kedvéért a Föld sugarának többszöröseiben fejezzük ki, akkor

r = n R

helyettesítéssel más alakban

\begin{matrix} v = \sqrt[]{\frac{G R^{2}}{n R}} = \sqrt[]{\frac{R G}{n}} \end{matrix}

(8)

lesz a körsebesség kifejezése. Közelítő számításoknál

\begin{matrix} G = 10 {m/sec}^{2} = 10 \cdot \frac{1}{1000} {km/sec}^{2} = \frac{1}{100} {km/sec}^{2}, \end{matrix}

a Föld sugara

6400

km (a pontos

6370

helyett!), tehát ezek helyettesítésével

\begin{matrix} v = \sqrt[]{\frac{64}{n} {km}^{2} / {sec}^{2}} = 8 km/sec \cdot \sqrt[]{\frac{1}{n}} . \end{matrix}

(9)

Mivel a Föld felszínére nézve

n = 1

, ennélfogva

8

km/sec vízszintes kilövési sebesség elegendő lenne a körpálya előállítására légüres térben. A sebesség (8) kifejezését a (6) baloldalába helyettesítve a keringésidő számára (a közös gyökjel alá hozatal és egyszerűsítés után) a

\begin{matrix} T = \frac{2 r π}{v} = \frac{2 n R π}{\sqrt[]{R G}} \sqrt[]{n} = 2 π \sqrt[]{\frac{R n^{3}}{G}} = 2 π \sqrt[]{\frac{6400 km n^{3}}{10^{- 2} {km/sec}^{2}}} = 6, 28 sec \cdot 800 \sqrt[]{n^{3}} \end{matrix}

kifejezést nyerjük, melynek numerikus része átszámitva

84

percet jelent s így végleges alakban

\begin{matrix} T = 84 perc \cdot \sqrt[]{n^{3}} . \end{matrix}

(10)

Mivel a Föld felszínén

n = 1

, ennélfogva itt

T = 84

perc, vagyis ellenállásmentes mozgás esetén a vízszintesen kilőtt test ennyi idő alatt kerülné meg a Földet. Az első mesterséges holdaknál

96

perc körüli keringési idő adódott, mert a vízszintes kilövés nem az

n = 1

értéknél, hanem valamivel magasabbról történt az utolsó rakéta-lépcső segítségével!
Ha a Föld felszínére vonatkozó értékeket az

n = 1

miatt kis

1

-es indexszel jelöljük, akkor a (9) és (10) értelmében

n = 4

esetben

v_{4} = \frac{v_{1}}{2}

és

T_{4} = 8 T_{1}

. Az utóbbit könnyű belátni abból, hogy most a megteendő út négyakkora, a sebesség ellenben félakkora, tehát a teljes körpálya leírásához tényleg

8

-szor akkora idő szükséges.
Hogy említett képleteink milyen jó közelítést adnak, kitűnik abból, hogy

n = 64

esetben

v_{64} = 8 / 8 = 1 km/sec

és

T_{64} = 84 perc \cdot 512 = 43 008 perc = 29, 9

nap, mert

\sqrt[]{64^{3}} = \sqrt[]{8^{6}} = 8^{3} = 512

és

1

nap

= 1440

perc. Mivel a Hold távolsága a Föld középpontjától valamivel több, mint

60 R

, kerületi sebessége

1, 023 km/sec

, keringési ideje pedig

27, 3

nap, ezek az adatok jól egyeznek az előbbi eredményekkel, mert a kérdéses nagyobb távolságból a Hold felé közeledve: a sebességnek (a megnövekedett vonzás miatt!) növekednie s emiatt a keringési időnek csökkennie kell.
2. A szökési vagy határsebesség az általános (4) képletből

a = \infty

helyettesítéssel nyerhető

v = \sqrt[]{\frac{2 k M}{r}}

alakban, mely a körsebességnek

\sqrt[]{2}

-szerese. Ekkor az ellipszis nagytengelye végtelenné válik, s így a pálya parabolába megy át. Ezt másként kritikus sebességnek is nevezik, mert ennél a test elhagyva a vonzó centrum erőterét, a végtelenbe távozik, vagyis mintegy kiszökik a vonzás hatása alól.
A következőkben néhány érdekes szökési sebességet közlünk:
1) A Föld mint vonzó centrum esetén a felszínre vonatkozólag

v = v_{1} \sqrt[]{2} = 11, 2

km/sec, a Holdnál valamivel nagyobb távolságban

v_{64} = v_{64} \sqrt[]{2} = 1, 41

km/sec,

n = 4 \cdot 10^{4}

esetben, vagyis valamivel több, mint

1, 5

-szeres naptávolságban a

v = 8 / 200 km/sec = 4 / 100 km/sec = 40 m/sec

körsebesség miatt mindössze

v = 1, 41 \cdot 40 m/sec = 56, 4 m/sec

lenne a kritikus sebesség.
2) A Nap, mint vonzó centrum esetén, mivel félátmérője

6, 95 \cdot 10^{10}

cm,

k = 6, 66 \cdot 10^{- 8} g^{- 1} {cm}^{3} {sec}^{- 2}

a gravitációs állandó,

M = 1, 98 \cdot 10^{33} g

a Nap tömege,

k M = 1, 337 \cdot 10^{26} {cm}^{3} {sec}^{- 2}

, tehát a Nap felszínére vonatkozó szökési sebességre nézve

\begin{matrix} v_{Nap}^{2} = \frac{2, 674 \cdot 10^{26} {cm}^{3} {sec}^{- 2}}{6, 95 \cdot 10^{10} cm} = 384748, 2 \cdot 10^{10} {cm}^{2} {sec}^{- 2}, \end{matrix}

amiből a gyökvonás elvégzése után

\begin{matrix} v_{Nap} = 620, 3 km/sec . \end{matrix}

3) Végül még arra vagyunk kíváncsiak, hogy a Naptól

150 \cdot 10^{6} k m = 1,5 \cdot 10^{13}

cm távolságra mekkora lenne a szökési sebesség? Képletünk szerint ekkor

\begin{matrix} v^{2} = \frac{2, 674 \cdot 10^{26} {cm}^{2} {sec}^{- 2}}{1, 5 \cdot 10^{13} cm} = 1783 \cdot 10^{10} {cm}^{2} {sec}^{- 2} \end{matrix}

amiből

\begin{matrix} v = 42, 2 km/sec . \end{matrix}

Mivel Földünk nem egészen

30

km/sec átlagos sebességgel végzi keringését a Nap körül, tehát igen messze vagyunk a kritikus sebességtől, s így nem kell félnünk attól, hogy el kell távoznunk ismeretlen csillagvilágok felé, ahová való utunkban a megfagyás veszedelme fenyegetné az emberiséget!