Cím: Sebességfeladatok megoldása vektorösszegzés segítségével
Szerző(k):  Fáy Árpád ,  Szenthe János 
Füzet: 1959/november, 147 - 150. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Gyakran szoktunk olyan kijelentést tenni, hogy egy mozgó pont, vagy test bizonyos sebességgel rendelkezik. Az ilyen kijelentésnek, ha szigorúan vesszük, mindig tartalmaznia kellene azt is, hogy mihez van viszonyítva az a sebesség, amivel az említett pont, illetve test rendelkezik; hiszen, ha jól meggondoljuk, nem lehet elképzelni olyan sebességet, amit ne valamihez viszonyítva mérnénk. (Természetesen a legtöbb esetben a rövidség kedvéért nem említjük meg, hogy mihez viszonyítottuk a szóbanforgó sebességet, mert az általában úgy is nyilvánvaló.) Az említettek után felvetődhet a következő kérdés: Ha ismerjük egy pontnak egy másik ponthoz viszonyított sebességét és ennek a pontnak egy harmadik ponthoz viszonyított sebességét, akkor hogyan lehet meghatározni az első pontnak a harmadik ponthoz viszonyított sebességét? Kérdésünkre a következő összefüggés ad feleletet: Ha az A pontnak a B ponthoz viszonyított sebessége vAB→ és a B pontnak a C ponthoz viszonyított sebessége vBC→, továbbá az A pontnak a C ponthoz viszonyított sebessége vAC→, akkor vAB→+vBC→=vAC→, ahol az összeadási jel természetesen vektorösszegezésre utal.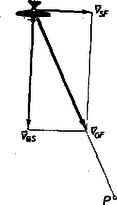
Az említett összefüggést lehet a következő egyszerűbb feladat megoldásánál alkalmazni: Egy repülőgép adott sebességű szélben repül. Motorjai a szél irányára merőleges irányban fejtik ki húzóerejüket. Mekkora sebességet kell a gépnek az áramló levegőhöz viszonyítva elérnie, ha állandó sebességgel repülve akar egy megadott pontot elérni? Legyen a szélnek a földhöz viszonyított sebessége vSF→, a gépnek a szélhez (áramló levegőhöz) viszonyított sebessége vGS→, a gépnek a földhöz viszonyított sebessége vGF→, akkor az említett összefüggés szerint vGF→=vGS→+vSF→. A fentiek szerint vSF→ adott; vGS→ iránya adott, a vSF→ irányára merőleges irány; ha a gép a kijelölt pontot állandó sebességgel akarja elérni vGF→ szintén adott irányú. A vektorösszegezési háromszögben adott, az említettek alapján egy oldal és a másik kettő iránya, tehát meghatározott a háromszög, így az oldalai is, ezáltal a vGS→ nagysága is, amit kerestünk.

 
 

A következőkben az említett sebességösszegezési összefüggés segítségével néhány feladatot fogunk megoldani.
I.

A dugattyút a körülvevő henger a CA egyenesen kényszeríti mozogni. A dugattyú a CB ,,hajtókarral'' hajtja az AB ,,forgattyút''. Az A, B, C pontok a csuklók középpontját jelölik, A pont rögzített.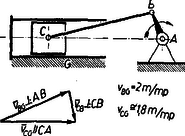
 
 
2. ábra
 

A szerkezet lerajzolt állapotában a B pont vBG→=2 m/mp sebességgel mozog. (A B pont sebességét az álló G géphez viszonyítottuk.) Meghatározandó a vCG→ sebesség.
Alkalmazható sebességösszegezési törvényünk: vCG→=vCB→+vBG→. Nézzük, mit tudunk a három fenti vektorról! vBG→ nagysága adott; vBG→=2 m/mp. vBG→ iránya, mivel B pont az A pont körül körön mozog, merőleges a kör sugarára: vBG→⊥BA, értelmét a forgásirány szabja meg. vCG→ iránya adott, mert C csak a CA egyenesen mozoghat: vCG→∥CA. vCB→ iránya is adott. Ennek meghatározására gondoljuk meg újból, hogy mit is jelent a B ponthoz viszonyított sebesség. Rögzítsük magunkat képzeletben a B ponthoz. Mit tapasztalunk? Az A pont B körül egy körön szalad körbe-körbe, mivel a mozgás során az AB távolság nem változik. A C pont hasonló okból a B körül egy köríven mozog. A körön mozgó pont sebessége merőleges a sugárra, tehát vCB→⊥CB. Ezekből az adatokból a sebességek vektorháromszöge megszerkeszthető, ismerjük ugyanis a háromszög egyik oldalát és a másik két oldal irányát. A megszerkesztett háromszögből vCG→-t lemérhetjük, vagy a szerkezet adatai alapján kiszámíthatjuk.
Megjegyezzük, hogy példánkban a két leggyakrabban előforduló kényszer szerepel. A ,,csukló'', mely a hozzácsatlakozó tagot önmaga körüli körmozgásra kényszeríti. A ,,csúszka'' (egyenesbevezető), mely két ,,tagot'' egymáshoz viszonyított egyenesvonalú mozgásra kényszerít. A ,,csúszkát'' esetünkben a dugattyú jelenti. Természetesen a ,,csúszkát'' technikailag nagyon sokféle módon lehet megvalósítani, például egy pálcára helyezett cső darabbal is.
Példánkból még egy figyelemreméltó következtetést vonhatunk le. Láthatjuk, hogy a forgattyú B pontjának pillanatnyi sebessége megszabja a dugattyú (C pont) sebességét. Sokan azt gondolják, hogy a dugattyú mozgását a hengerben levő gőz feszítőereje, vagy a robbanási folyamat szabja meg, hiszen ez hajtja a gépet. Ez tévedés. Gondoljunk egy egyenletes sebességgel szaladó gépkocsira. Kerekei és az áttételen keresztül a főtengely egyenletesen forog, így B pont egyenletes körmozgást végez. B pont sebességéből pedig, bármely pillanatban, a fenti szerkesztéssel megkapjuk a dugattyú sebességét. A dugattyú mozgását tehát függetlenül a hengerben lejátszódó folyamattól a gépkocsi mozgása szabja meg. Ezzel szemben a hajtórúdra átadódó hajtóerőt valóban az égés és a gázok nyomása határozza meg.
II.

Az ábrán rajzolt rudak csuklósan csatlakoznak egymáshoz. A és D csukló rögzített. B pont sebessége adott: vBG=30 m/mp. Meghatározandó a C pont sebessége.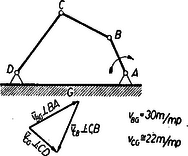
 
 
3. ábra
 

Az előző példához teljesen hasonlóan a sebességösszegezési összefüggés alkalmazásával adódik, hogy vCG→=vCB→+vBG→; továbbá vBG→⊥BA és vCB→⊥CB. Eltérést csupán az jelent, hogy most vCG→ irányát abból határozhatjuk meg, hogy C a D pont körül köríven mozog, tehát vCG→⊥CD. Ezek az adatok elegendők a három szög megszerkesztésére.
III.

Egy ping-pong játékos partnerének egy labdáját visszaüti. Ismert a labdának az ütőhöz érése előtti sebessége és a visszapattanás utáni sebessége, tudjuk azt is, hogy a játékos az ütőt az ütés pillanatában milyen irányban mozgatta; feltételezve, hogy az ütő és a labda ütközése rugalmas, meghatározandó, hogy mekkora sebességgel mozgatta a játékos az ütőt az ütés pillanatában.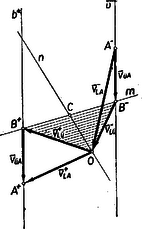
 
 
4. ábra
 

Legyen a labdának az ütőhöz viszonyított sebessége az ütközés előtt vLÜ-→ ütközés után pedig vLÜ⊤→, legyen a labdának az asztalhoz viszonyított sebessége ütés előtt vLA-→, ütés után pedig vLA÷→; ha a játékos az ütőt az ütés pillanatában vÜA→ sebességgel mozgatja akkor a bevezetőben említett sebességösszegzési összefüggés szerint vLA-→=vLÜ-→+vÜA→ és vLA+→=vLÜ-→+vÜA→. Mivel az ütközés rugalmas vLÜ-→ és vLÜ+→ az ütőre az ütközés pontjában emelt n merőlegessel egy síkban vannak és azzal egyenlő szöget zárnak be. A fentiek szerint adott vLA-→, vLA+→ és vÜA→ iránya, meg kell határozni vÜA→ nagyságát. Tekintsünk most az ábrára, mely az említett vektorok térbeli elhelyezkedését szemlélteti. Tekintve, hogy az A-, A+, B-, B+ pontok egy síkban vannak két eset lehetséges: 1. az említett pontok egy α síkot határoznak meg; 2. az említett pontok egy s egyenesen vannak.
1. Az A-A+ szakasz felezéspontja C az α sík és az n egyenes metszéspontja. A B+ és B- pontok a C pontban az n-re merőlegesen emelt β síkban vannak. Legyen b- az A- és B- pontok, b+ pedig az A+ és B+ pontok összekötő egyenese.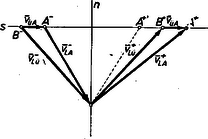
 
 
5. ábra
 

a. n nem merőleges b--ra és b+-ra; ebben az esetben az α és β síkok m metszésvonala kimetszi a b- és b+ egyenesekből a B- és B+ pontokat, tehát egyetlen megoldás van.
b. n⊥b-, b+, de n nem merőleges α-ra; ebben az esetben m és b-, b+ párhuzamosak, nincs megoldás.
c. n⊥α; ebben az esetben végtelen sok megoldás van.
2. Nem nehéz belátni, hogy ebben az esetben az n és s egyenesek merőlegesek egymásra és, ha A+' az A+-nak az n-re való tükrözésekor keletkezik, akkor A÷'A+=2vÜA→. (5. ábra).
Megjegyezzük, hogy az 1. c. és 2. esetek azok, mikor az ún. ,,nyesett labdák'' keletkeznek, természetesen az ilyen labdák különleges mozgása nem magyarázható az itt elmondottakkal, hanem lényegében a labda forgó mozgásának a következménye és így magyarázatánál további tényezőkkel (a labda kiterjedt volta, a labda és az ütő közötti súrlódás, légellenállás) kellene számolni.