Kezdőlap


Cím:	Az 1959. évi Arany Dániel Verseny II. fordulójának feladatai és megoldásuk 2.
Szerző(k):	Lőrincz Pál , Surányi János
Füzet:	1959/december, 161 - 166. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Haladók (II. osztályosok) versenye

1. feladat Egy szám két olyan tényezőre bontható, melyek különbsége

6

, negyedik hatványaik összege

272.

Melyik ez a szám?

I. megoldás: Ha a kisebbik tényezőt

x

-szel jelöljük, akkor a másik tényező

x + 6

, és a követelmény szerint

\begin{matrix} x^{4} + {(x + 6)}^{4} = 272. \end{matrix}

(1)

Szimmetrikusabbá válik azonban egyenletünk, ha a tényezők számtani közepét választjuk ismeretlennek. Ezt

z

-vel jelölve a két tényező

z - 3

és

z + 3

, így

\begin{matrix} {(z - 3)}^{4} + {(z + 3)}^{4} = 272, \end{matrix}

és rendezve

z

páratlan kitevős hatványai kiesnek:

\begin{matrix} z^{4} + 54 z^{2} - 55 = 0, \end{matrix}

vagyis

z^{2}

-ben másodfokú egyenletre jutunk. Ennek gyökei

z_{1, 2}^{2} = 1

-ből

z_{1} = 1

és

z_{2} = - 1

, a másik,

z_{3, 4}^{2} = - 55

gyökből

z_{3}

és

z_{4}

-re nem kapunk valós értéket. A

z_{1}

gyökhöz tartozó tényezőpár

- 2

és

+ 4

, a

z_{2}

-höz tartozó

- 4

és

+ 2

, a szorzat mindkét esetben

- 8

, ez az egyetlen (valós) szám, amely feladatunk követelményeinek megfelelhet. Valóban

{(- 2)}^{4} + 4^{4} = {(- 4)}^{4} + 2^{4} = 272

II. megoldás: Jelöljük a keresett számot

n

-nel, a feladat szerinti tényezőit

x

-szel és

y

-nal. Ekkor, feltéve, hogy

x > y

\begin{matrix} x - y = 6, \end{matrix}

(2)

\begin{matrix} x y = n, \end{matrix}

(3)

\begin{matrix} x^{4} - y^{4} = 272. \end{matrix}

(4)

Innen közvetlenül

n

-re is kaphatunk egyenletet, ha (3)-at és (4)-et

x (- y) = - n

x^{4} + {(- y)}^{4} = 272

alakban írva észrevesszük, hogy egyenleteink bal oldalán

x

és

- y

szimmetrikus függvényei állnak. Így (ugyanis várható, hogy a (2)-ből adódó

\begin{matrix} {[x + (- y)]}^{4} = 6^{4} = 1296 \end{matrix}

(5)

egyenlet bal oldalát, amely szintén szimmetrikus függvénye

x

és

- y

-nak, lehet úgy alakítani, hogy benne csak (2), (3) és (4) bal oldala szerepeljen. Valóban, kifejtés után

\begin{matrix} x^{4} - 4 x^{3} y + 6 x^{2} y^{2} - 4 x y^{3} + y^{4} - (x^{4} + y^{4}) - 4 {(x - y)}^{2} x y - 2 {(x y)}^{2} = 1296, \end{matrix}

tehát

\begin{matrix} 272 - 4 \cdot 6^{2} n - 2 n^{2} = 1296, n^{2} + 72 n + 512 = 0, \end{matrix}

és innen

n_{1} = - 8, n_{2} = - 64

.
Minthogy azonban (2)-ről (5)-re áttérve nem ekvivalens átalakítást végeztünk, ki kell próbálnunk, hogy a kapott számok kielégítik-e a feladat feltételeit. Evégett meg kell határoznunk az

x

y

tényezőket is. Ezeket (2) és (3)-ból számíthatjuk ki.

n_{1}

-gyel ugyanarra a két tényezőpárra jutunk, mint az I. megoldásban,

n_{2}

-höz pedig nem tartozik (valós) tényezőpár, ezt tehát nem tekinthetjük megoldásnak.

Megjegyzés. A versenyzők többsége indokolatlanul feltételezte, hogy a tényezők egész számok, ezekre azután (1), ill. (4)-ben végzett próbálgatással rá is jutott. Volt, aki csak azt tételezte fel, hogy a tényezők racionálisak, és kimutatta, hogy (ebben az esetben) a tényezők egész számok, továbbá, hogy a feladat túlhatározott, amennyiben a (2) egyenlet felesleges, mert 272 csak egyféleképpen írható két egész szám negyedik hatványának összegeként. ‐ Ámde a feladat szerint sem a két tényezőnek, sem magának a keresett szorzatnak nem kell még racionálisnak sem lennie! Tekintsünk két ellenpéldát. (2) és (3)-at változatlanul hagyva legyen pl. a tényezők negyedik hatványainak összege a kitűzött feladattól eltérően:

x^{4} + y^{4} = 386

; ekkor az előzőhöz hasonló számítással

x = \sqrt[]{2} + 3, y = \sqrt[]{2} - 3

n = - 7

adódik, tehát a keresett szám racionális, de a tényezők irracionálisok. Ha pedig (2) és (3)-at ismét meghagyva

x^{4} + y^{4} = 200

, akkor

x = \sqrt[]{\sqrt[]{748} - 27} + 3

y = \sqrt[]{\sqrt[]{748} - 27} - 3

n = \sqrt[]{748} - 36

, tehát a tényezőkkel együtt a keresett szám is irracionális.

2. feladat. Jelentsen

a

b

c

három olyan pozitív számot, amelyek közül kettő-kettőnek az összege legfeljebb

1

. Bizonyítsuk be, hogy

\begin{matrix} a^{2} + b^{2} + c^{2} \leq a + b + c - a b - b c - c a \leq \frac{1}{2} (1 + a^{2} + b^{2} + c^{2}) . \end{matrix}

(1)

Megoldás: A kettős egyenlőtlenség részeit külön-külön bizonyítjuk mindkét esetben annak megmutatásával, hogy a jobb és bal oldal különbsége nem lehet negatív. ‐ Valóban, az első egyenlőtlenség jobb és bal oldalának különbsége így írható:

\begin{matrix} a (1 - b - a) + b (1 - c - b) + c (1 - a - c) . \end{matrix}

(2)

A feltétel szerint

\begin{matrix} a + b \leq 1, b + c \leq 1, c + a \leq 1, \end{matrix}

(3)

így

\begin{matrix} 1 - b - a \geq 0, 1 - c - b \geq 0, 1 - a - c \geq 0, \end{matrix}

(4)

és ezeket rendre a pozitív

a

b

c

-vel szorozva és összeadva a bal oldalon (2)-t, a nem nagyobb jobb oldalon pedig 0-t kapunk. Ezzel (1) első részét bebizonyítottuk.
(2) akkor és csak akkor egyenlő 0-val, ha (4)-ben, és ezért már (3)-ban is mind a három helyen az egyenlőségi jel érvényes. Egyenlőségi jellel (3)-ban egyenletrendszer áll előttünk

a

b

c

-re; megoldása

\begin{matrix} a = b = c = \frac{1}{2}, \end{matrix}

(5)

ez a szükséges és egyben elegendő feltétele annak, hogy (1) első részében egyenlőség álljon fenn.
(1) második része jobb és hal oldalának különbségéről könnyen észrevehetjük, hogy egy teljes négyzet fele:

\begin{matrix} \frac{1}{2} (1 + a^{2} + b^{2} + c^{2}) - (a + b + c) + (a b + b c + c a) = \frac{1}{2} {(1 - a - b - c)}^{2}, \end{matrix}

tehát valóban nem lehet negatív. Így a bizonyítandó egyenlőtlenség második része is helyes. ‐ A két oldal akkor és csak akkor egyenlő, ha a négyzet alapja 0, vagyis

\begin{matrix} a + b + c = 1. \end{matrix}

(6)

Minthogy (5) és (6) egyidejűleg nem állhat fenn, azért

a

b

c

-nek nincs olyan értékrendszere, amely mellett (1)-ben egyidejűleg mindkét helyen az egyenlőség jele volna érvényes.
Megjegyzések. 1. Az utóbbi bizonyítás során nem használtuk ki a (3) feltételeket, sőt az

a

b

c

számok pozitívságát sem, ezért (1) második része

a

b

c

-nek bármely értékrendszere mellett fennáll. (Székely Jenő észrevétele.)
2. Más irányú általánosítása (1) második részének: tetszőleges

a_{1}, a_{2}, ..., a_{n}

számokra

\begin{matrix} (a_{1} + a_{2} + ... + a_{n}) - (a_{1} a_{2} + a_{1} a_{3} + ... + a_{1} a_{n} + a_{2} a_{3} + a_{2} a_{4} + ... + \\ + a_{2} a_{n} + a_{3} a_{4} + ... + a_{n - 1} a_{n}) \leq \frac{1}{2} (1 + a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2}) . \end{matrix}

Bizonyítása ugyanúgy történhet, ahogyan (1) második részét bizonyítottuk. (Fritz József dolgozatából.)
3. Az egyenlőtlenség első részének bizonyítását is átvihetjük 3 helyett bármilyen

n \geq 2

számú tagra. Ha ugyanis

a_{1}, a_{2}, ..., a_{n}

olyan pozitív számok, amelyek közül kettő-kettőnek az összege legfeljebb 1, akkor

\begin{matrix} 0 & \leq \frac{1}{2} {a_{1} [(1 - a_{1} - a_{2}) + ... + (1 - a_{1} - a_{n})] + a_{2} [(1 - a_{2} - a_{1}) + \\ + (1 - a_{2} - a_{3}) + ... + (1 - a_{2} - a_{n})] + ... + a_{n} [(1 - a_{n} - a_{1}) + \\ + ... + (1 - a_{n} - a_{n - 1})]} = \frac{n - 1}{2} [(a_{1} + ... + a_{n}) - \\ - (a_{1}^{2} + ... + a_{n}^{2})] - (a_{1} a_{2} + a_{1} a_{3} + ... + a_{n - 1} a_{n}) \end{matrix}

és innen átrendezéssel a következő általánosítást nyerjük:

\begin{matrix} \frac{n - 1}{2} (a_{1}^{2} + a_{2}^{2} + ... + a_{n}^{2}) \leq \frac{n - 1}{2} (a_{1} + a_{2} + ... + a_{n}) - (a_{1} a_{2} + a_{1} a_{3} + ... + a_{n - 1} a_{n}) . \end{matrix}

4. A kimondott általánosítások

n

-nek bármely

n \geq 2

értékére fennállanak, vagyis

n

minden olyan értékére, amely mellett az egyenlőtlenségeknek egyáltalán értelmük van.
5. Összefoglalva a 2. és 3. általánosítást az (1) kettős egyenlőtlenség következő általánosítását nyertük: Ha

a_{1}, a_{2}, ..., a_{n}

olyan pozitív számok, amelyek közül bármelyik kettőnek összege legfeljebb 1, akkor

\begin{matrix} \frac{n - 1}{2} (a_{1}^{2} + ... + a_{n}^{2}) \leq \frac{n - 1}{2} (a_{1} + ... + a_{n}) - (a_{1} a_{2} + ... + a_{n - 1} a_{n}) \leq \\ \leq \frac{1}{2} (1 + a_{1}^{2} + ... + a_{n}^{2}) + \frac{n - 3}{2} (a_{1} + ... + a_{n}) . \end{matrix}

A tett feltevés az első rész fennállásának elegendő, de nem szükséges feltétele már a feladatban szereplő

n = 3

esetben sem; pl.

n = 3

a_{1} = 1 / 4

a_{2} = 1 / 3

a_{3} = 3 / 4

esetében az egyenlőtlenség első része fennáll, bár

a_{2} + a_{3} > 1

. ‐ A második rész

a_{1}, a_{2}, ..., a_{n}

bármely értékei mellett fennáll.
6. Az (1) második része így is bizonyítható: nemnegatív számok mértani közepe nem nagyobb számtani közepüknél. Ezt az 1 és (

a + b + c

) pozitív számokra alkalmazva

\begin{matrix} \sqrt[]{1 (a + b + c)} \leq \frac{1 + (a + b + c)}{2} . \end{matrix}

(7)

Itt mindkét oldal pozitív, ezért a bal oldal négyzete sem nagyobb a jobb oldal négyzeténél:

\begin{matrix} a + b + c \leq \frac{1}{4} (1 + a^{2} + b^{2} + c^{2}) + \frac{1}{2} (a + b + c) + \frac{1}{2} (a b + b c + c a) . \end{matrix}

Innen pedig, 2-vel szorozva és a négyzetes tagok kivételével minden tagot a bal oldalra átvive (1) második részét kapjuk. ‐ (7)-ből is látható, hogy egyenlőség csak (6) fennállása esetén következik be.

3. feladat. Egy egyenlő szárú háromszög magasságpontja felezi az alaphoz tartozó magasságot. Szerkesszük meg a háromszöget, ha adott az alapot és a két szár meghosszabbítását érintő kör sugara.

I. megoldás: A keresett

A B C

háromszög (

A B = A C

) alakját megszerkeszthetjük annak alapján, hogy a körülírt kör középpontja a feltételnek megfelelő háromszögekben a szimmetriatengely alap felőli negyedelő pontjával esik egybe. Ez így látható be: legyen az alap felezőpontja

A_{1}

, a

B

-ből húzott magasság (amely átmegy az

A A_{1}

szakasz

M

felezőpontján) messe

A C

-t

D

-ben, az

A_{1}

-ből

A C

-re bocsátott merőleges talppontja legyen

E

. Mivel

M D

A A_{1} E

háromszögnek,

A_{1} E

pedig a

B C D

háromszögnek középvonala, ezért

A D = D E = E C

. Az

A C

oldal

F

felezőpontja tehát

D E

-t is felezi, így az

F

-ben

A C

-re emelt merőleges, ‐ amelynek

A A_{1}

-gyel való metszéspontja a háromszög köré írt kör

O

középpontja ‐ az

A_{1} E D M

derékszögű trapéz középvonala, s így felezi az

A_{1} M

szakaszt. Ezzel állításunkat igazoltuk.
Ennek alapján a keresett háromszöghöz hasonlót úgy szerkeszthetünk, hogy tetszőlegesen felvesszük az

A A_{1}

magasságot, ezen megszerkesztjük az

M

felező- és az

O

negyedelő pontot. Az

O

körül

O A

sugárral írt kör metszi ki az

A_{1}

pontban

A A_{1}

-re állított merőlegesből a háromszög

B

és

C

csúcsát.
Az

A B C

háromszögnek a kívánt méretre nagyítását pl. úgy végezhetjük, hogy az adott sugárral megrajzoljuk a ,,hozzáírt'' kört, majd ehhez az

A B C

háromszög oldalaival párhuzamos érintőket úgy szerkesztünk, hogy a kör a keletkezett háromszög alapját és szárainak meghosszabbítását érintse.

Megjegyzés. Ehhez a szerkesztéshez jutunk az Euler-egyenes tulajdonságainak felhasználásával is, de lényegében erre vezet az is, ha felhasználjuk, hogy a magassági pontot az oldalakra tükrözve a tükörkép a körülírt körre esik. Ismeretes ugyanis, hogy a háromszög

M

magassági pontja,

S

súlypontja ‐ amely mindhárom súlyvonalnak az oldal felőli harmadolópontja ‐ és körülírt körének

O

középpontja ebben a sorrendben egy egyenesen, a háromszög Euler-egyenesén van, ami egyenlő szárú háromszögnél egybeesik a szimmetriatengellyel, és

M S = 2 S O

. ‐ Második észrevételünk alapján pedig az

A A_{1}

szakasz

M

felezőpontjának

A_{1}

-re való

\bar{M}

tükörképét véve

\bar{A M}

-ben a körülírt kör egy átmérőjét nyertük.

II. megoldás: Gondoljuk a feladatot megoldottnak, és messe az

M

-en átmenő,

A C

-vel párhozamos egyenes

B C

-t

G

-ben. Ekkor

M G

A A_{1} C

háromszögnek középvonala, így

C G = G A_{1}

, másrészt

M G

merőleges

M B

-re. ‐ Ennek alapján a tetszőlegesen felvett

B C

alapon megszerkesztjük az

A_{1}

felező és

G

negyedelő pontot,

B G

mint átmérő fölé (Thalész-) félkört írunk, ebből az

A_{1}

-ben

B C

-re emelt merőlegessel kimetsszük

M

-et, végül

A_{1}

-et

M

-re tükrözve kapjuk a keresetthez hasonló

A B C

háromszög hátralevő

A

csúcsát.

III. megoldás: Legyen egy tetszés szerinti

A B C

egyenlő szárú háromszögben (

A B = A C

) a

B C

alap felezőpontja

A_{1}

és az

A A_{1}

szakasz felezőpontja

M

. Meg fogjuk mutatni, hogy a

B M

egyenes és az

A C

oldal

D

metszéspontjából

A A_{1}

-re bocsátott merőleges

T

talppontja az

A A_{1}

szakasz

A

felőli harmadoló pontja, függetlenül a háromszög alakjától. ‐ Ezt tudva a keresett háromszög alakja megszerkeszthető. Egy

a

egyenes egy

A_{1}

pontjában

A A_{1}

merőlegest szerkesztünk, és megszerkesztjük

A A_{1}

-nek az

A

felőli

T

harmadoló pontját. Ekkor az összes olyan

A B C

egyenlő szárú háromszögekben, amelyeknek alapja az a egyenesen van, az alap végpontjait

A A_{1}

felező pontjával összekötő egyeneseknek a szemközti oldallal való metszéspontja a

T

-ben

A A_{1}

-re merőlegesen húzott

t

egyenesen van.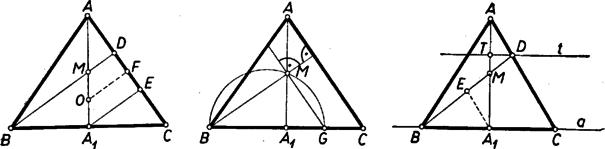

Ennek kell azt a

D_{0}

pontját kikeresnünk, amelyre

A D_{0}

és

B D_{0}

vagy azt, amelyre

A D_{0}

és

C D_{0}

merőlegesek, az ilyen pontokat pedig az

A M

szakasz mint átmérő fölé rajzolt (Thalész-) kör metszi ki

t

-ből. Legyen a kör és az egyenes két metszéspontja

D_{0}

és

D_{0}^{*}

; ezek

A A_{1}

-re szimmetrikusan helyezkednek el, így mindkettőt összekötve

A

-val és az összekötő egyeneseket meghosszabbítva, amíg

a

-t metszik (mondjuk

B

-ben, ill.

C

-ben) egyenlő szárú háromszöget kapunk. Ebben a

B

-t

M

-mel összekötő egyenes

A C

-t annak

t

-vel való metszéspontjában, vagyis

D_{0}^{*}

-ban metszi. Ez rajta van a Thalész-körön is, tehát

B D_{0}^{*}

A C

oldalra bocsátott magasság. Így valóban megszerkesztettük a keresett háromszög alakját ‐ amennyiben a

T

pontra vonatkozó állításunk igaz.
Ennek igazolására húzzunk

A_{1}

-ből párhuzamost

A C

-vel, messe ez

B D

-t

E

-ben.

A_{1} E

B C D

háromszög középvonala, s így

E

felezi a

B D

szakaszt. Másrészt

E M

és

M D

egyenlő, mert

A M D

és

A_{1} M E

háromszögek megfelelő oldalai, ezek pedig egybevágók, ugyanis

A M

és

A_{1} M

oldaluk egyenlő,

M

-nél levő szögeik csúcsszögek,

A

-nál és

A_{1}

-nél levő szögeik pedig váltószögek. ‐ Ekkor azonban

M D

B M

szakasz harmadrésze, s így az

A_{1} B M

és

T D M

hasonló derékszögű háromszögekből (az

M

-nél levő szögek csúcsszögek) nyerjük, hogy

T M

is harmadrésze

A_{1} M

-nek, tehát hatoda

A A_{1}

-nek. Így

A_{1} T

kétharmada és

A T

harmadrésze

A A_{1}

-nek, amint állítottuk.

IV. megoldás. Számítás alapján egy olyan szerkesztést is megadhatunk, amelyben nem szükséges egy hasonló háromszög közbeiktatása.
Jelöljük a háromszög alapját és magasságát

a

-val, ill.

m

-mel, az

a

-val szemközti szögét

α

-val. Legyen az alapot és a szárak meghosszabbítását érintő körnek középpontja

K

(az

A A_{1}

magasság, egyben szögfelező meghosszabbításán), az

A B

egyenesen levő érintési pontja

H

és sugara az adott

ϱ

. Messe a

K H

egyenes a

B C

egyenest az

L

pontban és legyen

A_{1} L = x

. Ezt az

x

hosszúságot fogjuk kiszámítani, majd megszerkeszteni.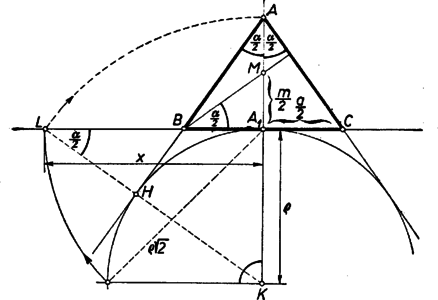

Merőleges szárú hegyes szögekként

B A A_{1} ∢ = K L A_{1} ∢ = α / 2

és

C A A_{1} ∢ = M B A_{1} ∢ = α / 2

, ezért a

K L A_{1}

és

B A A_{1}

, valamint

C A A_{1}

és

M B A_{1}

derékszögű háromszögek hasonlók. A második és az első, ill. a negyedik és az első háromszögből a befogókra:

\begin{matrix} \frac{a}{2} : m = ϱ : x, ill. \frac{m}{2} : \frac{a}{2} = ϱ : x . \end{matrix}

E két aránypárból (egyenletből)

m

-et kiküszöbölve

a

is kiesik (ez úgy is végrehajtható, hogy a két aránypárt tagról tagra összeszorozzuk és egyszerűsítünk), így

x

és

ϱ

között kapunk összefüggést:

\begin{matrix} x^{2} = 2 ϱ^{2}, \end{matrix}

és innen

x = ϱ \sqrt[]{2}

.
Ennek alapján szerkesztésünk a következő: a

ϱ

sugarú körhöz tetszés szerinti

A_{1}

pontjában érintőt szerkesztünk, erre

A_{1}

-től mindkét irányban felmérjük

ϱ \sqrt[]{2}

-t vagyis a

ϱ

befogójú egyenlő szárú derékszögű háromszög átfogóját. A végpontokat a kör

K

középpontjával összekötő egyenesek kimetszik a körből a szárak meghosszabbításainak érintési pontjait.
Megjegyzések. 1.

A

-t a

K A_{1}

félegyenesből

K A = K L

alapján is kimetszhetjük (a

K L A_{1}

és

K A H

derékszögű háromszögek egybevágók).
2. Több versenyző lényegében a legutóbbi gondolatmenettel

α / 2

-t határozta meg: helyesen erre jutott:

{tg}^{2} α / 2 = 1 / 2

, ebből négyzetgyökvonással és trigonometriai táblázattal meghatározta a szöget, és azt szögmérővel felmérte. ‐ Ez az eljárás azonban nem tekinthető (euklidészi) szerkesztésnek.
3. A keresetthez hasonló egyenlő szárú háromszög akkor is megszerkeszthető, ha ‐ a feladattól eltérően ‐ az

M

magasságpontnak felezés helyett valamely más, előírt arányban kell osztania az

A A_{1}

szakaszt. Megoldásaink megfelelő módosítással az

A_{1} M : M A = 1 : k

előírás esetén is használhatók, kivéve az I. megoldást, amelyben lényegesen kihasználtuk, hogy

k = 1

(a hozzáfűzött megjegyzések azonban használhatók). A feladatnak

k

minden (pozitív) értéke mellett egy és csakis egy megoldása van, és ez áll akkor is minden

k < 1

-re, ha

M

-et

A A_{1}

meghosszabbításán kell kapnunk.