Cím: Az 1959. évi Arany Dániel Verseny II. fordulójának feladatai és megoldásuk 1.
Füzet: 1959/november, 83 - 88. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye.

 

1. feladat: Bontsuk fel 5/8-ot minden lehetséges módon három olyan pozitív tört összegére, amelyeknek a számlálója 1.
 

Megoldás: Olyan a, b, c természetes számokból álló hármast kell keresnünk, amelyre
58=1a+1b+1c.(1)
Feltehetjük, hogy a a legkisebb, c a legnagyobb nevező a hármasban (egyenlőség persze nincs kizárva), vagyis
(0<)a≤b≤c.(2)
Eszerint reciprok értékeik közül 1/a a legnagyobb és 1/c a legkisebb:
1a≥1b≥1c(>0).(3)
Tájékozódjunk a nagyságáról. Evégett (1) jobb oldalán a második és harmadik tagot (3) alapján előbb a nem kisebb 1/a-val, majd a biztosan kisebb 0-val helyettesítjük; így olyan két egyismeretlenes egyenlőtlenséget kapunk, melyeknek 1/a a nagyobb, ill. a kisebb oldalán áll:
58=1a+1b+1c≤1a+1a+1a=3a,innena≤245<5,58=1a+1b+1c>1a,innena>85>1.


Ezek szerint a-ra három lehetőség van: a=2, a=3, vagy a=4.
1. Keressünk először a=4-hez megfelelő b-t és c-t. (1)-ből
1b+1c=58-14=38.(4)
A fenti meggondolás első felét b-re ismételve (3) alapján
38=1b+1c≤1b+1b=2b,tehátb≤163(<6).
Másrészt most (2) szerint b is legalább 4, tehát b=4, vagy b=5. Ezekkel (4)-ből c=8, ill. c=40/7 adódik, de az utóbbi nem egész szám. ‐ Eszerint a=4 mellett egy felbontást kapunk:
58=14+14+18.(1)

2. Legyen most a=3. Ekkor (1) így alakul
1b+1c=58-13=724,(5)
innen a fentiekhez hasonlóan
724=1b+1c≤1b+1b=2b,tehátb≤487<7,
eszerint most a b=3, 4, 5 és 6 lehetőségek jönnek szóba. A megfelelő c-értékek (5)-ből: c=-24, c=24, c=120/11, ill. c=8. Csak a második és a negyedik érték természetes szám, így két felbontást kapunk:
58=13+14+124=13+16+18.(II, III)

3. Végül az a=2 esetben (1)-ből
1b+1c=58-12=18.

Itt alkalmas átalakítással közvetlenül áttekinthetjük az összes b, c értékpárokat. Távolítsuk el a törteket, gyűjtsünk minden tagot az egyenlet jobb oldalára, és igyekezzünk a kifejezést szorzattá alakítani:
8b+8c=bc,0=bc-8b-8c=(b-8)(c-8)-64.
Eszerint 64-et kell minden lehető módon két egész tényezőre bontani. A tényezőkre (2) folytán b-8≤c-8, másrészt nem lehet a két tényező negatív, mert akkor a kisebbre b-8≤-8, b≤0 adódnék. Így a lehetséges felbontások:
b-8=1,32,14,18,c-8=64,32,16,8,
és ezekből a következő felbontások adódnak:
58=12+19+172=12+110+140=12+112+124=12+116+116.(IV‐VII)



Mindezek szerint 5/8-ra az előírt alakban a fenti hét (I)‐(VII) felbontás lehetséges.
 

Megjegyzés. Az a=3 esetben adódott
58=13+13-124
felbontás mutatja, hogy ha elejtjük a pozitívság követelményét, akkor a feladatnak több megoldása van. A fentihez hasonló gondolatmenettel további 6 ilyen felbontást találunk:
58=11+18-12=12+17-156=12+16-124=12+14-18;58=11-14-124=11-16-18.



2. feladat: Szerkesszünk háromszöget, ha ismerjük egy oldalát (a), az ezzel szemközti szöget (α), és annak a szakasznak a hosszát, amely az α szög csúcsát a háromszög beírt körének középpontjával összeköti.
 

I. megoldás: Gondoljuk a feladatot megoldottnak, legyen a keresett háromszög ABC, ebben BC=a, BAC∢=α és ‐ O-val a beírt k kör középpontját jelölve AO=d az adott szakasz.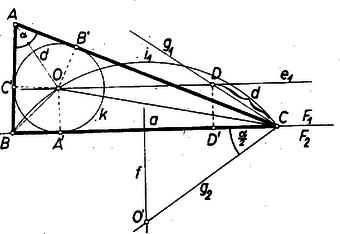
 
 

Legyenek továbbá k-nak az oldalakon levő érintési pontjai A', B', C' és sugara ϱ. Az OBC háromszögben
COB∢=180∘-OBC∢-OCB∢=180∘-β2-γ2=90∘+180∘-β-γ2=90∘+α2.
Eszerint O csak azon az i1, i2 körívpáron lehet, amelynek (B és C-től különböző) pontjaiból az adott BC szakasz a megszerkeszthető 90∘+α2 szögben látható. Másrészt megszerkeszthetjük OB'=ϱ-t, mert az AOB' derékszögű háromszög alakját a d átfogó és az α/2 hegyesszög meghatározza, ‐ és evvel még egy mértani helyet kapunk O-ra, ugyanis O csak a BC-től ϱ távolságban fekvő e1, e2 párhuzamos egyeneseken lehet.
Ezek alapján a szerkesztés a következő. Felvesszük a BC=a szakaszt és kijelöljük, hogy a háromszöget a BC egyenessel létrejött F1 és F2 félsíkok közül F1-en kívánjuk kapni. F1-en fekszik O is, elég lesz tehát az i1-et és e1-et megszerkesztenünk. CB-re a C csúcsban mindkét félsíkon felmásoljuk az α/2 szöget, a szárak g1, g2, megszerkesztjük BC-nek f felező merőlegesét, majd g2 és f-nek O' metszéspontja körül O'B=O'C sugárral megrajzoljuk i1-et. e1-et pedig úgy kapjuk, hogy g1-re C-ből felmérjük d-t, és ennek D végpontján át BC-vel párhuzamost húzunk. i1 és e1 közös pontja O, ennek vetülete BC-re A' és OA'=ϱ, ezek alapján megrajzoljuk a k kört. Most már az A csúcsot a B és C-ből k-hoz húzott második érintők metszéspontja adja. (Ezek céljára C', B'-t a B körül BA', ill. C körül CA' sugárral írt körrel metszhetjük ki.)
Szerkesztésünk helyes, mert a BCO' egyenlő szárú háromszög O'-nél levő szöge kétszerese α/2 pótszögének, azaz 180∘-α, ez egyben a O' középpont körül O'B sugárral írt kör F1-beli i1 ívéhez tartozó középponti szög. Így a kör F2-beli ívéhez 180∘+α nagyságú középponti szög tartozik, tehát a BOC kerületi szög ennek fele: 90∘+α/2. Most már a C'BC és B'CB szögek összege kétszerese az OBC és OCB szögek összegének, a BOC szög kiegészítő szögének, 90∘-α/2-nek, azaz 180∘-α-val egyenlő, tehát a szerkesztett érintők A-nál valóban α szöget zárnak be (az a szögük ekkora, amelynek terében a BC szakasz van). AO felezi az A-ból k-hoz húzott érintők szögét, ezért OAB'∢=α/2=DCB∢, továbbá D-nek BC-n levő vetületét D'-vel jelölve az AOB' és CDD' derékszögű háromszögekben OB'=OA'=DD', így e két háromszög egybevágó, tehát AO=CD=d.
A szerkesztés lépései O előkészítéséig egyértelműen végrehajthatók (α nyilván 0∘ és 180∘ közti szög, így fele hegyesszög). i1 és e1 közös pontjainak száma szerint O-ra 2, 1, 0 pontot kapunk, és ezekből ugyanennyi háromszöget, mert a további lépések ismét egyértelműek. Ha 2 megoldás adódik, ezek egybevágók, mert egymásnak f-re nézve tükrös párjai, így a feladatnak lényegében legfeljebb 1 megoldása van.
 

II. megoldás: Az adott α szög az a oldal látószöge az A csúcsból, ennek alapján ismert módon megszerkeszthetjük a keresett háromszög k* körülírt körét.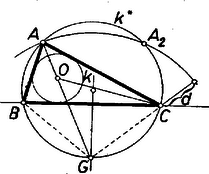
 
 

A BAC szög AO felezője k*-ot másodszor az A-t nem tartalmazó BC ívnek G felezőpontjában metszi, mert a kerületi szögek tétele szerint GBC∢=GAC∢=GAB∢=GCB∢=α/2, tehát a BCG háromszögben GB=GC, és e húrokhoz egyenlő ívek tartoznak. Másrészt CO felezi az ACB szöget, ezért az OCG háromszögben OCG∢=(γ+α)/2. Ekkora a COG szög is, mint az ACO háromszög külső szöge, tehát a COG háromszög egyenlő szárú: OG=CG. Így A-nak G-től való távolsága AG=AO+OG=d+CG.
Ezek alapján a szerkesztés a következő. k*-ban a BC-re merőleges átmérőnek az a végpontja G, ahonnan BC látószöge 180∘-α. (Ez is mutatja, hogy G azonos az I. megoldásban használt O'-vel.) A GC szakasznak C-n túli meghosszabbítására rámérjük d-t. A G körül d+CG sugárral leírt kör k*-ból kimetszi A-t. Aszerint, hogy a d+CG szakasz kisebb, ill. nagyobb k* átmérőjénél, ill. éppen egyenlő vele, 2, 0, ill. 1 megoldást kapunk. ‐ Szerkesztésünk helyessége bizonyításául csak azt kell megmutatnunk, hogy a kapott A pontot G-vel összekötő szakasznak A-tól d távolságra, azaz G-től CG távolságra fekvő O* pontja azonos az ABC háromszögbe írt kör középpontjával. Valóban, a CGO* háromszög egyenlő szárú, és benne CGO*∢=CBA∢=β, így O*CG∢=90∘-β/2, ennélfogva O*CB∢=O*CG∢-BCG∢=O*CG∢-α/2=90∘-(α+β)/2=γ/2, vagyis O*C felezi a C-nél fekvő szöget. Másrészt O* az A-nál fekvő szög felezőjén is rajta van, tehát O*=O.
 

III. megoldás: Az előbbi AOB' háromszöggel egybevágó háromszöget szerkesztve megkapjuk AB'-t, az A-ból k-hoz húzható érintőszakaszt. Erről ismeretes, hogy egyenlő s-a-val, ahol s a háromszög kerületének fele. Ebből (a szokásos jelölésekkel) b+c=2s-a=2(s-a)+a alapján előállíthatjuk az A csúcsból kiinduló oldalak összegét, ezzel pedig a feladatot visszavezettük a háromszögnek az a, b+c, α adathármasból való ismert szerkesztésére: az A* csúcsú α/2 szög egyik szárára felmérjük b+c-t, ennek B végpontjából a sugarú körívvel a másik szárból kimetsszük C-t, majd A*C felező merőlegesével az első szárból A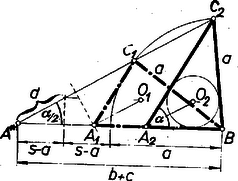-t.
 
 

A körívnek a szög szárával 2, 1, 0 közös pontja, egyszersmind ennyi megoldás van. Két metszéspont esetén mindkettő A*-nak ugyanazon oldalára esik (különben a>b+c volna), ezért A1 és A2 az A*B szakaszra esnek. Az így adódó A1BC1 és A2C2B háromszögek egybevágók. Ugyanis az A*C1A1 és A*C2A2 egyenlő szárú háromszögek külső szögeként C1A1B∢=C2A2B∢=α, másrészt A*C1A1∢=A*C2A2∢=α/2. C1BA1∢=ε jelöléssel BC1A1∢=180∘-α-ε, így C2C1B∢=180∘-(180∘-α-ε)-α/2=ε+α/2. Ámde a BC1C2 háromszög egyenlő szárú, ezért C1C2B∢=ε+α/2, tehát A2C2B∢=ε. Így a kérdéses háromszögek egy oldalban és két megfelelő szögben megegyeznek, valóban egybevágók.
 

IV. megoldás: α és d ismeretében megszerkeszthető O, k és α szárainak az érintési pontig terjedő szakasza: s-a. Ezzel egyúttal (s-a)+a=s is ismert, a csúcstól ekkora távolságban érinti α szárait az a oldalt kívülről érintő k1 hozzáírt kör, így ez is megszerkeszthető.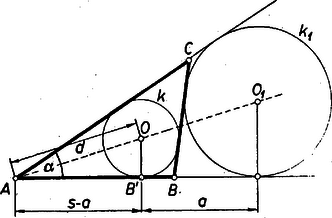
 
 

Most már k és k1 közös belső érintőinek az α szög szárai közé eső szakasza az a oldal.
 

3. feladat: Bizonyítsuk be, hogy ha
ax+by+cz=0és(1)xa+yb+zc=1,(2)
akkor
x2a2+y2b2+z2c2=1.(3)

 

Megoldás: A (2) feltételi egyenlőség négyzete alkalmas rendezéssel így írható:
1=x2a2+y2b2+z2c2+2(xyab+yzbc+zxca)==x2a2+y2b2+z2c2+2xyzabc(cz+ax+by).
A második zárójelbeli kifejezésben ráismerünk (1) bal oldalára, amely 0-val egyenlő. Ennek figyelembevételével kapott egyenlőségünk azonos (3)-mal, a bizonyítandó állítással.
Az (1) és (2) feltevéseknek csak úgy van értelmük, ha az a, b, c, x, y, z számok 0-tól különbözők, így pedig az alkalmazott átalakítások megengedett azonos átalakítások voltak.
Megjegyzés. A látottaknál valamivel több ismeret felhasználásával az állítás így is bizonyítható. x/a, y/b, z/c-t u, v, w-vel jelölve ezek 0-tól különböző valós számok, feltételeink szerint
u+v+w=1,1u+1v+1w=0,amibőlvw+wu+uv=0,(4)
és u2+v2+w2-et kell meghatároznunk. (4) első és harmadik kifejezése együtthatóként szerepel a T=(t-u)(t-v)(t-w) kifejezésnek t hatványai szerint rendezett polinomalakjában, eszerint uvw-t d-vel jelölve
T=t3-(u+v+w)t2+(uv+vw+wu)t-uvw=t3-t2-d.(5)
Hozzuk most két módon polinomalakra a T*=(t2-u2)(t2-v2)(t2-w2) szorzatot. Egyrészt
T*=(t-u)(t-v)(t-w)[-(-t-u)(-t-v)(-t-w)]=TT',
ahol T' annak a kifejezésnek (-1)-szerese, amely T-ből t-nek -t-vel való helyettesítésével áll elő; ennélfogva T'=-[(-t)3-(-t)2-d]=t3+t2+d, és így T*=(t3-t2-d)(t3+t2+d)=t6-t4-2dt2-d2.
Másrészt az (5)-höz hasonló kifejtéssel
T*=t6-(u2+v2+w2)t4+(u2v2+v2w2+w2u2)t2-u2v2w2.
A két polinomalakból az egyező fokú tagok együtthatóinak összehasonlításából kapjuk a bizonyítandó
(x2a2+y2b2+z2c2=)u2+v2+w2=1
egyenlőséget, továbbá leolvashatjuk az
(x2y2a2b2+y2z2b2c2+z2x2c2a2=)u2v2+v2w2+w2u2=-2d=-uvw(=-2xyzabc)(6)
összefüggést is. Ebből az is látszik, hogy u, v, w közül kettő pozitiv és egy negatív kell hogy legyen. Ez valóban leolvasható a (4) feltételi egyenletekböl is: a második szerint nem lehet mindhárom egyező előjelű; ha pedig kettő, pl. v és w negatív, akkor az első egyenlet szerint mindkettő abszolút értéke kisebb, mint u-é, tehát 1u kisebb |1v| és |1w|-nél, így 1u+1v negatív, és ez méginkább áll 1u+1v+1w-re.
A (6) azonosság közvetlenül is nyerhető a feltételi egyenletekből:
u2v2+v2w2+w2u2=(uv+vw+wu)2-2uvw(u+v+w)=-2uvw.