Cím: Az 1959. évi Arany Dániel Verseny I. fordulójának feladatai és megoldásuk
Szerző(k):  Lőrincz Pál ,  Lukács Ottó ,  Scharnitzky Viktor ,  Surányi János 
Füzet: 1959/október, 41 - 48. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye.
1. feladat: Két csoportba oszthatjuk-e a következő 10 számot úgy, hogy az egyik csoportba tartozók összege 9-cel legyen nagyobb, mint a másik csoportba tartozók összege: -7, -4, -2, 3, 5, 9, 10, 18, 21, 33?

 
I. megoldás: Vonjuk ki az adott számok összegéből, 86-ból, a készítendő csoportok összegének eltérését, 9-et. A maradékot, 77-et két egyenlő részre osztva kapnók a kisebb összegű csoport összegét. De máris látjuk, hogy a kívánt felosztás lehetetlen, mert 77 páratlan, a fele nem egész, adott számaink viszont valamennyien egészek.
 
Megjegyzések. 1. Lényegében ugyanígy bizonyították a kívánt felosztás lehetetlenségét azok is, akik a kisebb összegű csoportban szereplő számok összegét x-szel jelölve ‐ így a másik csoport összege x+9 ‐ az x+(x+9)=86 egyenletről mutatták meg, hogy megoldása tört szám.
2. Több versenyző úgy vélte megoldani a feladatot, hogy elhagyta az adott számok között szereplő 9-et, és azt mutatta meg, hogy a fennmaradt számok nem oszthatók két egyenlő összegű csoportba. Bármennyire hasonlít is ez a gondolat a fenti megoldáshoz, ‐ mégsem azonos vele, és nem teljes bizonyítás. Ebből csak azt látjuk, hogy olyan megoldása nincs a feladatnak, melyben a 9-es a nagyobb összegű csoportba tartozik. Olyan megoldás viszont még nem lehetetlen, amelyben a 9-es a kisebb összegű csoport tagja. Ha pl. az adottak helyett a 9, 2, 2, 2, 2, 2, 2, 2, 2, 2 számokat kellene ugyanazon követelmény mellett két csoportba osztani, ez lehetséges: a kisebb összegű csoportban egyedül a 9-es áll, a másikban a 2-esek, bár ‐ mint könnyű belátni ‐ a 9-es itt sem lehet a nagyobb összegű csoportnak tagja.
3. Általában: adott egész számokat nem lehet úgy két csoportra osztani, hogy a csoportok összegének eltérése adott egész szám legyen, ha a számok összegéből az előírt eltérést levonva páratlan számot kapunk. De ha így páros szám adódik, ebből még nem következik, hogy a kívánt csoportosítás lehetséges. Pl. a 9, 2, 2, 2, 2, 2, számcsoport nem osztható ketté követelményünk szerint, bár összegüknek és az eltérésnek különbsége osztható 2-vel: (19-9):2=5.
4. Megállapításunk több csoportra a következőképpen általánosítható. Adott egész számok k számú, adott, egész eltérésű csoportra való felbonthatóságának szükséges ‐ de, mint láttuk, nem elegendő ‐ feltétele az, hogy a számok összegéből az eltérések összegét levonva k-val osztható számot kapjunk. (Ez az összeg úgy értendő, hogy valamennyi csoport összegének egy bizonyos, kijelölt számcsoport összegétől való eltéréseit vesszük, előjelükkel együtt.)
 
II. megoldás: A feladat ezt kívánja: alkossunk a felsorolt egész számokból olyan két csoportot, hogy a bennük levő számok összegének különbsége 9 legyen, a két összeg összeadva pedig 86-ot adjon. Ez lehetetlen, mert ha két egész szám különbsége páratlan, akkor a két szám ellentétes párosságú, és ezért összegük is páratlan.
 
2. feladat: Húzzuk meg egy szabályos ötszög két egymást metsző átlóját. Bizonyítsuk be, hogy ezek olyan darabokra osztják egymást, amelyek közül a nagyobbik egyenlő az ötszög oldalával.
 
I. megoldás: Legyen az ABCDE szabályos ötszög AC és BD átlóinak metszéspontja F. Az AF=AB egyenlőséget abból mutatjuk meg, hogy az ABF háromszögnek BF-en fekvő két szöge egyenlő (1. ábra).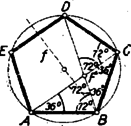
 
 
1. ábra
 

Minden (konvex) ötszög szögeinek összege 3⋅180∘=540∘. A szabályos ötszög szögei egyenlők, így egy-egy szöge 108∘. Az ötszög köré írható körből az oldalak, mint egyenlő húrok, egyenlő íveket metszenek le. Az ötszög mindegyik szögének szárai között három ilyen ív fekszik, ezért mindegyik ív az ötszög csúcsaiból 108∘:3=36∘-nyi szögben látható. Eszerint BAF∢=BAC∢=36∘, ABF∢=ABD∢=2⋅36∘=72∘, így AFB∢=180∘-(36∘+72∘)=72∘=ABF∢, amit bizonyítani akartunk.
Az AF szakasz az AC átlónak nagyobbik darabja: AF>FC, mert az ABF háromszögben AF, az egyik 72∘-os szöggel szemben fekvő oldal, nagyobb BF-nél, a 36∘-os szöggel szemben fekvő oldalnál, BF pedig egyenlő FC-vel, mert a BCF háromszög ‐ két 36∘-os szöge révén ‐ ugyancsak egyenlő szárú.
Hasonlóan látható be, hogy DF=DC, és hogy DF>FB. ‐ Ezzel a bizonyítást befejeztük.
 
Megjegyzések. 1. A bizonyítás első része csak azt használta fel, hogy a (rövidebb) BC ív egy, és hogy a (rövidebb) DA ív két ötödrésze a kör kerületének. Eszerint az AF=AB egyenlőség érvényes marad akkor is, ha a DA ívet a körön elforgatjuk (2. ábra). ‐ Vegyük észre, hogy az E csúcs a bizonyítás egyik részében sem szerepel.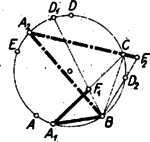
 
 
2. ábra
 

2. Az AFB∢=ABF∢ egyenlőséget a mértékszámok kiszámítása nélkül is megmutathatjuk. Az ABD szög két ötszögoldalhoz tartozó íven nyugvó kerületi szög, a CBD és ACB kerületi szögek pedig egy-egy ilyen íven nyugszanak. Így az utóbbiak összege egyenlő az ABD szöggel, másrészt ez az összeg a BCF háromszög külső szögeként a BFA szöggel is egyenlő. ‐ Itt viszont csak azt használtuk fel, hogy az ABCD húrnégyszög oldalai által lemetszett körívekre fennáll az AB^+CD^=AD^ egyenlőség. Tehát tulajdonképpen a következő általánosabb tételt bizonyítottuk be: ha az ABCD húrnégyszögben fennáll az AB^+CD^=AD^ egyenlőség, akkor AF=AB és DF=DC, ahol F az AC és BD átlók metszéspontja. (Mindkét átlónak van egy oldallal egyenlő darabja, ahogyan az eredeti tétel is állítja.)
Ennek a tételnek egy más bizonyítása: az A körül AB sugárral írt k1 körnek az ABCD négyszög k körülírt körével való második közös pontját E-vel jelölve (3. ábra) DE^=AD^-AE^=AD^-AB^=DC^, tehát a D körül DC sugárral írt k2 kör szintén E-ben metszi k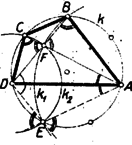-t.
 
 
3. ábra
 

Így EDA∢=BDA∢=FDA∢ és EAD∢=CAD∢=FAD∢, tehát az AE egyenes az AF-nek, DE a DF-nek tükörképe AD-re, vagyis E az F tükörképe AD-re. Eszerint AF=AE=AB és DF=DE=DC; egyszersmind F a k1 és k2-nek második közös pontja. (Az E pont megfelel a szabályos ötszög ötödik csúcsának.) ‐ Az állítás hurkolt négyszögre is érvényes, hacsak B és C a k ugyanazon AD ívének pontjai (4. ábra; a 3-4. ábrákon A, B, C, D egy-egy szabályos 7-, ill. 9-szög csúcsai közül valók).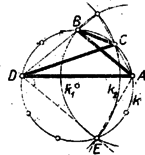
 
 
4. ábra
 

II. megoldás: A kívánt egyenlőséget abból bizonyítjuk, hogy az AFDE négyszög paralelogramma. Az I. megoldás szerint a CDE szög 108∘, a DCA szög 72∘, egymásnak kiegészítő szögei. Ámde tudjuk, hogy ha két szög egymást 180∘-ra egészíti ki, és egyik pár száruk párhuzamos ‐ vagy egybeeső ‐, második száraikba pedig az elsőkből ellentétes irányú forgással jutunk ‐ amint az említett szögek közös CD szárából DE-be negatív (az óramutató forgásával egyenlő irányú) forgás visz át, CA-ba pedig pozitív ‐, akkor a második szárak ‐ itt DE és AC ‐ szintén párhuzamosak. Ugyanígy a BD átló párhuzamos az AE oldallal. Az így létrejövő AFDE paralelogrammából AF=ED és DE=AE, amit bizonyítani akartunk.
 
Megjegyzés. Számos versenyző szemlélet alapján elfogadta, hogy a szabályos ötszög mindegyik átlója párhuzamos egy oldallal, vagy más szóval, hogy pl. az ACDE négyszög trapéz. Ezt valamivel indokolni kellett volna. Lehet így is: az ED oldal f felező merőlegese szimmetriatengelye az ötszögnek, tehát A és C egymásnak tükörképei f-re. Ezért AC merőleges f-re, és így párhuzamos ED-vel.
 
3. feladat: Melyek azok a háromjegyű természetes számok, amelyekben a számjegyek összege harmadrészére csökken, ha magához a számhoz 3-at adunk?
 
Megoldás: A keresett N szám egyes helyi értékű jegyeként csak 6-nál nagyobb jegyek jöhetnek szóba, mert különben a 3-mal nagyobb N' szám harmadik jegye legfeljebb 9 lenne, vagyis nagyobb lenne N harmadik jegyénél, első két jegye egyeznék N-ével, tehát N' jegyeinek összege nem lehetne kisebb N jegyeinek összegénél.
Így N utolsó jegye 7, 8, vagy 9, ezért ettől N' utolsó jegye a tízes összevonás folytán +3-10=-7-tel tér el, vagyis 7-tel kisebb, az összevont 1 tízest pedig N tízeseihez adjuk hozzá. Aszerint, hogy ez a jegy 9-nél kisebb, vagy 9-cel egyenlő, a továbbiakra két eset adódik; a százas jegy csak az utóbbiban változik meg.
Ha a tízes helyi értékű jegy N-ben kisebb 9-nél, akkor N'-ben 1-gyel nagyobb, tehát N' jegyeinek összege csak 7-1=6-tal kisebb N-énél. Ez a csökkenés N jegyei összegének kétharmad része, tehát N jegyeinek összege 9. ‐ Ha már most N utolsó jegye 7, akkor első két jegyének összege 2, innen N-re 207, 117 és 027 adódik, az utóbbi azonban nem valódi háromjegyű szám. Hasonlóan kapjuk ‐ utolsó jegynek 8-at, 9-et véve ‐ a 108, 018 és 009 számokat.
N tízes helyi értékű jegyét 9-nek véve N' tízes jegye 9+1=10-ből 0-nak, azaz 9-cel kisebbnek adódik, százas jegye pedig 1-gyel nagyobbnak ‐ hacsak nem N százas jegye is 9. Ha N százas jegye kisebb 9-nél, akkor N' százas jegye 1-gyel nagyobb, tehát N' jegyeinek összege 7+9=16-tal csökken és 1-gyel nő, azaz végeredményben 15-tel csökken. Ez azonban nem lehet egész szám két harmadrésze, s így a feladatnak ilyen megoldása nincs. ‐ Ha végül N százas jegye is 9 volna, akkor N' jegyeinek összege 7+9+9=25-tel csökkenne és ‐ az ezres helyi értékben ‐ 1-gyel nőne, tehát 24-gyel csökkenne. ‐ Ebből a jegyek összege 36 lenne, ami lehetetlen, mert háromjegyű szám jegyeinek összege legfeljebb 3⋅9=27, ‐ tehát ilyen megoldás sincs.
Ezek szerint feladatunknak csak a 207, 117 és 108 számok tehetnek eleget. Mindhárom meg is felel, mert a 3-mal nagyobb 210, 120, 111 számban a jegyek összege 3, harmada a 9-nek.
 
Megjegyzések. 1. Sok versenyző próbálgatás útján találta meg a fenti számokat. Ezzel persze nem bizonyították, hogy csak ez a három megoldás van. ‐ Többen kellő indokolás nélkül kimondták, hegy a jegyek összege csak 9 lehet, vagy hogy az utolsó jegy csak 7, 8, vagy 9 lehet. Mindezek nem tekinthetők teljes értékű megoldásnak.
2. Tetszetősen indul, de sokkal több munkával vezet célhoz a következő gondolatmenet. Mivel N' jegyeinek s' összege harmada N jegyei összegének, azért N jegyeinek összege: s=3s', osztható 3-mal, és ezért ugyanez áll magára N-re is. Így N'=N+3 is osztható 3-mal, ezért ez áll s'-re is: s'=3k, és így s=9k. Háromjegyű számban a jegyek összege legfeljebb 27, így s=9, vagy 18, vagy 27. Könnyű belátni, hegy 999, az egyetlen 27 jegyösszegű háromjegyű szám, nem megoldás, de az s=18 lehetőségnek vizsgálata hosszadalmas. Az s=9 feltevésből ‐ a fentihez hasonlóan ‐ könnyen adódik a három megoldás.
 
Lukács Ottó, Scharnitzky Viktor

 
Haladók (II. osztályosok) versenye.
 
1 feladat. Mutassuk meg, hogy a
3(p+2)x2-px-(4p+7)=0
egyenletnek p bármely (valós) értéke mellett van (valós) gyöke.
 
I. megoldás: A bizonyítandó állítás fennállásának szükséges és egyben elégséges feltétele, hogy az egyenlet diszkriminánsa D≥0 legyen p bármely értéke mellett. A diszkrimináns
D=p2+12(p+2)(4p+7)=49p2+180p+168,(1)
és ez p-nek másodfokú függvénye. E függvény képe parabola, így elég azt bizonyítanunk, hegy e parabola minden pontja a p abszcissza-tengely fölött, vagy a tengelyen helyezkedik el. Helyettesítésekkel nyerjük, hogy a parabola egyes pontjai valóban a p-tengely fölött vannak, pl. p=0 esetén D=+168. Minthogy a parabola folytonos vonal, ezért, ha volna pontja a p-tengely alatt is, akkor metszenie kellene a tengelyt, és az ilyen pontra D=0 volna. Ámde a
49p2+180p+168=0(2)
egyenlet diszkriminánsa
D1=1802-4⋅49⋅168<0,
tehát a (2) egyenletnek nincs (valós) gyöke, és az (1) parabola valóban nem metszi a p tengelyt, egészen a p-tengely fölött helyezkedik el.
 
Megjegyzés. Nem lehet elfogadni (2) gyökeinek megvizsgálása helyett a parabola néhány pontjának ábrázolása után a szemléletre való hivatkozást. Számos versenyző így ,,bizonyított''.
 
II. megoldás: (1) átalakításával pusztán számviszonyok alapján is belátható, hogy D a p-nek minden értéke mellett nagyobb 0-nál:
D=49p2+180p+168=(7p+907)2+13249.
E kifejezés első tagja p bármely értéke mellett pozitív, vagy 0, mert négyzet, a második tagja pozitív.
Ezzel az állításnál valamivel többet bizonyítottunk be. Miután D határozottan nagyobb 0-nál, az adott egyenletnek p bármely (valós) értéke mellett két különböző (valós) gyöke van.
 
2. feladat. Legyen x pozitív szám. Bizonyítsuk be, hogy
1+x3>1+x3.(1)

I. megoldás:
(1+x3)3=1+3⋅x3+3⋅x29+x227.
Mivel x pozitív, ezért a jobb oldal minden tagja pozitív. Elhagyva az utolsó két tagot, a jobb oldal kisebbé válik:
(1+x3)3>1+x.(2)

Innen mind a két oldalból köbgyököt vonva a bizonyítandó állításra jutunk.
Meg kell még mutatnunk, hogy (2)-ről (1)-re következtetve nem követünk el hibát, vagyis a köbgyökvonás helyes bizonyítási lépés. Bizonyítjuk, hogy ha tetszés szerinti a3, b3 számokra
a3>b3,
azaz
a3-b3>0,(3)
akkor
a>b,(4)
azaz
a-b>0.

Ugyanis (3) bal oldalát tényezőkre bontva nyerjük, hogy
a3-b3=(a-b)(a2+ab+b2)=(a-b)[(a+b2)2+34b2]>0.
Mivel a-b-nek az utolsó alakbeli szorzója pozitív, egyenlőtlenségünk helyes marad, ha avval osztjuk. Ezzel éppen a bizonyítandó (4) egyenlőtlenségre jutunk.
 
Megjegyzés. A kérdéses szorzó 0 is lehet, ti. ha egyszerre fennáll a+b/2=0 és b=0. Ezekből azonban ellentétbe jutunk feltevésünkkel, ugyanis a=-b/2=0 és így a3=b3(=0).
 
II. megoldás: Akárhány x1, x2,...,xn szám számtani közepén értjük az x1+x2+...+xnn számot, mértani közepén pedig az x1x2...xnn számot. Általánosan is igaz a következő, n=2 esetére közismert egyenlőtlenség: Ha az x1, x2,...,xn számok mindegyike pozitív, akkor a mértani közepük nem nagyobb, mint a számtani közepük. Egyenlőség akkor és csakis akkor áll fenn, ha x1=x2=...=xn.* Legyen most n=3, x1=x2=1, x3=1+x, ekkor feltevésünknél fogva x3>x1, és így a hivatkozott tétel alapján
1+1+1+x3>1⋅1⋅(1+x)3,
ami bizonyítandó volt.
 
Megjegyzések. Eszerint tételünk már x>-1-től kezdve fennáll, mert már ekkor teljesül x3=1+x>0, kivéve mégis az x=0 esetet, amikor a két oldal egyenlő.
A bizonyítandó állítás más irányú általánosítása: Legyen x>-1, x≠0 és n>1, egész szám, ekkor
1+xn>1+xn.
Mind a két általánosításra rámutatott dolgozatában Bollobás Béla.
Meg lehet mutatni, hogy a szóban forgó egyenlőtlenségnek az x>-9, x≠0 számok tesznek eleget.
 
3. feladat. Egy ABC háromszöget forgassunk el a C csúcsa körül 60∘-kal és jelöljük az elforgatott háromszöget A'B'C'-vel (C'≡C). Bizonyítsuk be, hogy az A'B, B'C és C'A szakaszok felezőpontjai egy szabályos háromszög csúcsai.
 
Megoldás: A kérdéses felezőpontokat rendre P, Q, R-rel jelölve azt bizonyítjuk, hogy a PQR háromszögnek QP és QR oldalai egyenlők és egymásból 60∘-os elforgatással állnak elő. Evégett a BC oldal D felezőpontját segítségül véve megmutatjuk, hogy a QDP háromszög 60∘-os forgatással áll elő a QCR háromszögből.
 
 

A QD szakasz a CB'B szabályos háromszögnek középvonala, így a CQD háromszög is szabályos, tehát a Q pont D-ből az eredeti forgatással áll elő, és QD=QC; továbbá QD ugyanazon irányú 60∘-os forgatással keletkezik QC-ből, mint amelyikkel CQ a CD-ből, vagyis amelyik forgatással A'B'C'-t az ABC-ből képeztük. Hasonlóan a DP szakasz a CBA' háromszögnek középvonala, így fele a CA' oldalnak, egyszersmind CA-nak is ‐ mert a CA'A háromszög szabályos ‐, tehát egyenlő CR-rel; továbbá DP-nek és CA'-nek iránya ugyancsak az eredeti forgatással áll elő CA, azaz CR irányából.
Ezek szerint a QDP szög szárai a QCR szög száraiból ugyanakkora és ugyanazon irányú forgatással állnak elő, tehát e két szög egyenlő. Egyenlők a QDP és QCR háromszögeknek e szögek megfelelő szárain fekvő oldalai is, így a két háromszög egybevágó, és egymáshoz képest valóban 60∘-kal vannak elfordulva. Ennélfogva harmadik megfelelő oldalpárjukra QP=QR, és RQP∢=60∘, amit bizonyítani akartunk.
Megjegyzések. 1. Az ábra több más módon is kiegészíthető oly egybevágó háromszögekkel, amelyek segítségével a PQR háromszög két oldalának egyenlősége bizonyítható. A versenyzők általában a fenti bizonyításénál bonyolultabb utakat követtek; alig volt két versenyző, aki egyformán bizonyított volna. Egyesek nem vették észre, hogy könnyű meghatározni a PQR háromszög két oldalának szögét, ehelyett külön bizonyították be további két oldal egyenlőségét.
2. Az előbbi gondolatmenettel bizonyítható tételünknek következő általánosítása. Ha az ABC háromszögnek a C csúcsa körüli 60∘-os elforgatása után az A'B, CB' és AC' szakaszokat tetszőleges, de ugyanazon arány szerint osztjuk (pl: mindegyiket harmadoljuk), az osztópontok szabályos háromszöget alkotnak.
3. Néhány versenyző észrevette bizonyítandó tételünk kapcsolatát a következő tétellel:* ,,Az OAB és OA'B' ellentétes körüljárású szabályos háromszögek O csúcsa közös. Bizonyítsuk be, hogy ... az AA', OB és OB'... szakaszok felezőpontjai szabályos háromszög csúcsai.'' ‐ A versenyfeladatban az ABC háromszög 60∘-os elforgatása során keletkező CAA' és CB'B háromszögek C csúcsa közös, és körüljárásuk ellentétes. Ábránk betűzését úgy átírva, hogy a közös csúcs jele C, ill. C' helyett O legyen, a többi csúcsé pedig A, B, A' és B' helyett rendre B, A', A és B', tüstént látjuk, hogy az idézett állítás éppen a PQR háromszög szabályosságát mondja ki.
4. A feladatot felfoghatjuk úgy is, hogy az AA'C és C'BB' egyező körüljárású szabályos háromszögek megfelelő csúcsait összekötő szakaszok felezőpontjairól mutattuk meg, hogy újabb szabályos háromszöget alkotnak. Ebben a formában a feladat lényegesen általánosítható, amennyiben sem a közös csúcsnak, sem a háromszögek szabályos voltának nincs benne lényeges szerepe.
Legyen ABC és A1B1C1 két hasonló, egyező körüljárású háromszög, ekkor az AA1, BB1, CC1 szakaszok A2, B2, C2 felezőpontjai is az ABC háromszöghöz hasonló és egyező körüljárású háromszöget alkotnak.
Ez a tétel is könnyen bizonyítható komplex számok segítségével,* de a versenyfeladat fenti bizonyításához hasonlóan is bizonyítható.
Nevezzük az állításban szereplő háromszögeket a csúcsok indexezésének megfelelően H, H1 és H2 háromszögnek. Összekötve C-t az A1 és B1 csúccsal is, a keletkező szakaszok felezőpontja legyen A* és B*. Mivel A*B*C2 ‐ amit a továbbiakban H*-gal fogunk jelölni ‐ H1-nek C-ből felére kicsinyített képe, így elég H2 és H*-ról megmutatni, hogy hasonlók és egyező körüljárásúak.
 
 

A2A* és A*C2 mint az AA1C, ill. A1CC1 háromszög középvonala párhuzamos és egyirányú az AC, ill. A1C1 szakasszal és fele akkora. Hasonlóan B2B* és B*C2 mint a BB1C, ill. B1CC1 háromszög középvonala a BC, ill. B1C1 szakasszal párhuzamos, egyező irányú és fele akkora. Így az A2A*C2 háromszögben az A*-nál levő szög és B2B*C2-ben a B*-nál levő szög egyaránt annak a szögnek a kiegészítő szögével egyenlő, amellyel H1-el van forgatva H-hoz képest, az ezeket a szögeket közrefogó oldalak aránya pedig (mindkétszer a fönti sorrendben véve) H és H1 megfelelő távolságainak arányával egyezik meg. Ebből következik, hogy az A2A*C2 és B2B*C2 háromszögek hasonlóak és egyező körüljárásúak. Ekkor azonban A2C2 az A*C2-ből és B2C2 a B*C2-ből egyező irányú és nagyságú elforgatással és ugyanolyan arányú nyújtással keletkezik, s így ugyanezzel az elforgatással és nyújtással keletkezik H2 is H*-ból. Ezzel állításunkat igazoltuk.
A bizonyítás könnyen láthatóan abban az esetben is érvényben marad, ha egyes szereplő háromszögek egyenesszakasszá fajulnak. Ez bekövetkezik akkor is, ha H és H1 szerepét a versenyfeladat AA'C és C'BB' háromszögének adjuk át. Ekkor A* a C≡C' ponttal esik egybe, B*-nak pedig a feladatmegoldás D pontja felel meg.
 
Lőrincz Pál, Surányi János

*Bizonyítását lásd pl. Kürschák ‐ Hajós ‐ Neukomm ‐ Surányi: Matematikai Versenytételek I. 111. o.

* Lásd Reiman István: Geometriai feladatok megoldása a komplex számsíkon, 48. feladat, 63. és 71. o. Tankönyvkiadó 1957, Középiskolai Szakköri Füzetek.

*Lásd ugyanott, 77. o. 9. Példa.