Kezdőlap


Cím:	Az 1959. évi Országos Verseny I. fordulójának feladatai és megoldásuk
Füzet:	1959/szeptember, 4 - 8. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Hány olyan megoldása van az

\begin{matrix} | x | + | y | < 1000 \end{matrix}

egyenlőtlenségnek, amelyben

x

és

y

egész számok?

I. megoldás: Mindkét ismeretlen értéke csak a

0

\pm 1

\pm 2, ..., \pm 999

számok egyike lehet, de az egyik értékének megválasztása korlátozást jelent a másikéra. Menjünk végig

x

minden egyes értékén, és állapítsuk meg a mellette lehetséges, vele megoldást adó

y

-értékek számát; kérdésünkre ezen számok összege adja meg a választ. ‐ Vegyük először

x

nemnegatív értékeit.

x = 0

mellett

| y | < 1000

, azaz

- 1000 < y < 1000

, ennek

- 999

- 998, ..., - 1

0

1, ...,999

tesznek eleget, számuk

2 \cdot 999 + 1 = 1999

x = 1

mellett

| y | < 999

, az előbbinél

2

-vel kevesebb megoldás van, mert

y = \pm 999

már nem felel meg.
Általában is,

x

valamely értékéről az

1

-gyel nagyobbra áttérve

| y |

-nek legnagyobb lehetséges értéke

1

-gyel kisebbnek adódik, így

y

előbbi értékei közül kettőt kell törölnünk, az

x

y

megoldások száma

2

-vel csökken. Így a megoldások számai

x = 0,1,2, ...,999

-re számtani sorozatot alkotnak. Az utolsó tag

x = 999

-cel

: 1

, a tagok száma 1000, és így összegük:

\begin{matrix} \frac{1000 (1999 + 1)}{2} = 1000^{2} . \end{matrix}

x = - 1

- 2, ..., - 999

esetén

| x | = 1,2, ...,999

, így az előzőkhöz hasonlóan az ilyen megoldások együttes száma

\begin{matrix} 1997 + 1995 + ... + 1 = 999^{2} . \end{matrix}

Ezzel valamennyi megoldást figyelembe vettük, összes számuk:

1000^{2} + 999^{2} = 1 998 001

II. megoldás: A kérdés egyértelmű a következővel: hány olyan

x

y

egész számpár van, amelyre az

| x | + | y |

összeg vagy

0

-val, vagy

1

-gyel, vagy

2

-vel,

...

, vagy

999

-cel egyenlő? Állapítsuk meg tehát általában az

| x | + | y | = k

egyenlet egész számokban való megoldásainak

N_{k}

számát, ‐ ahol

k

nemnegatív egész szám ‐, és képezzük ezek összegét

k = 0

1

2

...

999

-re.

k = 0

esetén egy megoldás van:

x = y = 0

k = 1

esetén négy megfelelő értékpár van:

1

0

;

- 1

0

;

0

1

;

0

- 1

k \geq 2

esetén a megoldásokat két csoportba osztjuk aszerint, hogy fellép-e bennük a

0

szám, vagy nem. Az elsőbe a

k = 1

esethez hasonlóan

4

megoldás jut:

k,0

;

- k,0

;

0, k

;

0, - k

. A második csoportban

| x |

a következő

k - 1

értéket veheti fel:

\begin{matrix} | x | = j = 1,2,3,...,k - 1, \\ és evvel| y |is meg & van határozva: \\ | y | = k - j = k - 1,k - 2,k - 3,...,1. \end{matrix}

j

minden fenti értékével az előjelek figyelembevétele során

2 \cdot 2 = 4

megoldás adódik, mert

j

és

k - j

mindegyike számára egymástól függetlenül

2

-féleképpen választhatjuk az előjelet:

\begin{matrix} j, k - j; - j, k - j; j, - (k - j); - j, - (k - j), \end{matrix}

tehát itt a megoldások száma

4 (k - 1)

. ‐ Végeredményben

k \geq 2

esetén a megoldások száma

4 + 4 (k - 1) = 4 k

. Ez a kifejezés

k = 1

esetén is helyes, ekkor a második csoportba nem tartozik megoldás;

k = 0

-ra azonban nem érvényes.
Ezek után

k = 0

1

2

...

999

-re

\begin{matrix} N = 1 + 4 (1 + 2 + 3 + ... + 999) = 1 + 4 \cdot \frac{999 \cdot 1000}{2} = 1 998 001. \end{matrix}

Megjegyzés. Ugyanígy, ha s nemnegatív egész szám, akkor az

| x | + | y | < s

egyenlőtlenség megoldásainak száma egész számokban:

\begin{matrix} N_{s} = 1 + 4 [1 + 2 + 3 + ... + (s - 1)] = 2 s^{2} - 2 s + 1. \end{matrix}

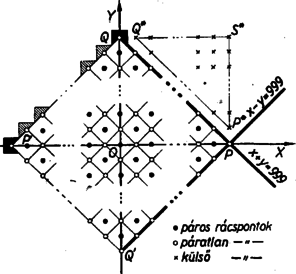
III. megoldás: Minden egyes megoldást a derékszögű koordinátarendszerben egy ún. rácspont ábrázol, vagyis olyan pont, amelynek mindkét koordinátája egész szám. Jellemezzük e rácspontok helyzetét, majd ennek alapján számukat megállapítva adjunk választ kérdésünkre.

Az adott egyenlőtlenség így is írható:

\begin{matrix} | x | + | y | \leq 999. \end{matrix}

Tekintsük átmenetileg csak azokat a megoldásokat, amelyekben

x

és

y

egyike sem negatív. Így

| x | = x

és

| y | = y

, teljesül tehát

\begin{matrix} x \geq 0, y \geq 0 és x + y \leq 999. \end{matrix}

(1)

Az ezen korlátozásoknak eleget tevőrácspontok nem lehetnek az

x = 0

egyenestől (az

Y

-tengelytől) balra, az

y = 0

-tól (

X

-tengely) lefelé, és az

x + y = 999

egyenestől ,,jobbra fölfelé''. Más szóval: (1)-nek csak az ezen három egyenessel bezárt

O P Q

derékszögű háromszög csúcsaiban, oldalszakaszain és belsejében fekvő rácspontok tehetnek eleget, ahol

O

P

és

Q

koordinátái:

(0,0)

(999,0)

és

(0,999)

.
Fordítva: ha valamely

x

y

rácspont eleget tesz ezen geometriai előírásoknak, akkor az

x

y

számpárra, továbbá ‐ negatív értékeket ismét megengedve ‐ vele együtt a

- x

y

, az

x

- y

és a

- x

- y

párokra is teljesül az adott egyenlőtlenség. Az utóbbi számpároknak megfelelő rácspontok azoknak az

O P' Q

O P Q'

, ill.

O P' Q'

háromszögeknek a kerületén és a belsejében vannak, amelyek

O P Q

-ból az

Y

-ra,

X

-re, ill.

O

-ra való tükrözéssel keletkeznek. A négy háromszög együtt hézagtalanul kitölti a

P Q P' Q'

négyzetet, ahol

P' (- 999,0)

és

Q' (0, - 999)

.
Számuk megállapítása céljára e négyzet rácspontjait többféleképpen rendezhetjük.
a) Valamelyik tengellyel, pl. az

Y

-nal párhuzamos sorok (rácsegyenesek) szerinti számlálással lényegében az I. megoldást ismételjük. ‐ Hasonlóan a II. megoldás is értelmezhető pontszámlálásként, meggondolásunkat a

P Q P' Q'

-höz hasonló helyzetű azon négyzetek kerületein való számlálás szemlélteti, melyeknek közös középpontja

O

, és átlója rendre

2

4

6

...

1998

egység, és ehhez hozzávesszük az origót. (

x

y

-on valós számokat értve pl.

| x | + | y | = 999

P Q P' Q'

négyzet kerületének egyenlete.)
b) A

P Q P' Q'

négyzet oldalaival párhuzamos rácsegyenesek mentén való számlálásban célszerű a rácspontokat két csoportra, páratlanokra és párosakra osztani az

x + y

összeg páratlan, ill. páros volta szerint, és a számlálást csoportonként végezni. Ugyanis

P Q

vagy

P Q'

irányú mozgással sem páros rácspontból páratlanba nem lehet átjutni, sem fordítva, így a pontok e két irányra nézve nem egyszerű hálót alkotnak, számuk nem állapítható meg puszta szorzással. Valóban, a

P Q

irányú egyenesek egyenlete

x + y = c

alakú, ahol

c

állandó, tehát ezeken mozogva

x + y

párossága is változatlan; és ugyanez áll

P Q'

irányú egyenesen való mozgás esetén is, mert egyenletük

x - y = d

alakú, ahol

d

állandó, és két egész szám különbsége ugyanolyan párosságú, mint az összege. ‐ Minden rácspont vagy páros, vagy páratlan. Könnyen belátható, hogy páratlan rácspontjaink

P Q

és

P Q'

-vel párhuzamosan ezer-ezer sort alkotnak, számuk

1000^{2}

, a párosaké pedig hasonlóan

999^{2}

.
c) Rácspontjaink számát különbségként is megkaphatjuk: véve a

P

és

P'

, ill.

Q

és

Q'

pontokon át az

Y

, ill.

X

-tengellyel párhuzamos egyenesek által határolt négyzet

1999^{2} = 3 996 001

rácspontját, és ebből elhagyva a

P Q P' Q'

-négyzeten kívül, a négy sarki háromszögben fekvőket, mint számunkra feleslegeseket. Ez utóbbiak együttes száma

4 (1 + 2 + ... + 999) = 1 998 000

. A jobb felső ilyen háromszög csúcsai:

P^{*} (999,1)

Q^{*} (1,999)

és

S^{*} (999,999)

. Így

N = 3 996 001 - 1 998 000 = 1 998 001

.
d) A rácspontok száma területszámítás útján is megállapítható. Rendeljük hozzá minden

R

rácsponthoz annak az egységnyi oldalú ,,elemi'' négyzetnek a területét, amelynek középpontja

R

és oldalai párhuzamosak a tengelyekkel. Így ‐ ha valamely, a koordinátarendszerben fekvő idom területe csupa ilyen négyzetre bontható fel, ‐ akkor annyi rácspontot tartalmaz, ahány egységnyi a területe. ‐ Vegyük hozzá a

P Q P' Q'

négyzethez a kerületén fekvő rácspontokhoz tartozó elemi négyzeteknek a

P Q P' Q'

-n kívül fekvő részeit, így egy ,,fogazott négyzetet'' kapunk. A

P

Q

P'

Q'

rácspontok elemi négyzetéből egyenkint

3 / 4

területegységnyi rész fekszik ,,kívül'', összesen

3

egység, a

P Q

Q P'

P' Q'

Q' P

oldalszakaszok belsejében fekvő

4 \cdot 998 = 3992

rácspontéból pedig egyenkint

1 / 2

területegységnyi rész, összesen

1996

egység. Mivel még

\bar{P Q} = 999 \sqrt[]{2}

, azért a fogazott négyzet területe

2 \cdot 999^{2} + 3 + 1996 = 1 998 001

egység, megegyezésben fentebbi eredményünkkel.

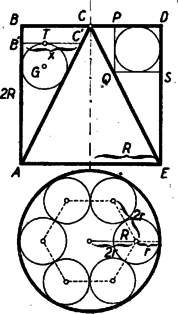
2. feladat. Egyenes henger alakú edényünk magassága egyenlő alapkörének átmérőjével. Az álló edénybe előbb egy vele egyenlő alapsugarú és magasságú egyenes kúpot helyezünk ‐ csúcsával fölfelé ‐, majd

6

egyenlő sugarú gömböt. A gömbök mindegyike érinti az edény falát, a kúp palástját és

2

másik gömböt. Kiemelkednek-e a gömbök az edényből?

I. megoldás: A henger és a kúp közös tengelyén átmenő bármely

A B C D E

síkmetszetben az

A B

henger- és az

A C

kúpalkotó ugyanakkora

B A C

szöget zár be. Így

r

sugaraik egyenlősége folytán mind a

6

gömb középpontja ugyanolyan mélyre esik le, középpontjaik egy vízszintes síkban helyezkednek el. Ezek nyilván egy olyan

2 r

oldalú szabályos hatszög csúcsai, amelynek középpontja a henger tengelyén van, ezért a gömbközéppontoknak a tengelytől való távolsága ugyancsak

2 r

, a henger falától való távolságuk

r

; így a henger (és a kúp) sugara:

R = r + 2 r = 3 r

Tekintsünk egy olyan tengelymetszetet, amely átmegy egy gömbnek

G

középpontján. A gömbből így kimetszett főkör érinti az

A B

, ill.

A C

alkotókat. Tekintsük e főkör érintőjét a gömb legmagasabban fekvő

T

pontjában, és jelöljük ennek az alkotók (vagy meghosszabbításaik) közti szakaszát

B' C' = x

-szel. Így adataink alapján az

A B' C'

derékszögű háromszögben

A B' = 2 x

A C' = \sqrt[]{5} x

. A főkör ezen háromszögnek beírt köre, ennélfogva szokásos jelölésekkel és az ismert összefüggés alapján:

\begin{matrix} r = \frac{t}{s}, azaz r = \frac{x^{2}}{x \frac{3 + \sqrt[]{5}}{2}} = \frac{x}{\frac{3 + \sqrt[]{5}}{2}} . \end{matrix}

Ennek alapján

\begin{matrix} \frac{x}{R} = \frac{3 + \sqrt[]{5}}{6} < \frac{2 + \sqrt[]{9}}{6} = 1, \end{matrix}

és mivel

R

pozitív, azért

x < R

. Eszerint

B' C' < B C

, és az

A B' C'

és

A B C

háromszögek hasonlósága alapján

A B' < A B

, tehát

T

alatta van a fedőlap

B D

szintjének, a gömbök nem emelkednek ki az edényből.

II. megoldás: Ha már megkaptuk az

r = R / 3

összefüggést, akkor szinte számítás nélkül is válaszolhatunk a kérdésre a következő átfogalmazás alapján:
Beilleszthető-e egy gömb az edénybe (a kúp után) úgy, hogy érintse a henger falát és legmagasabb pontja a fedőlap szintjében legyen? Látható, hogy igen. Ugyanis a gömb főkörmetszetét befoglalva egy

2 r

oldalú

D P Q S

négyzetbe, ennek az a

Q

csúcsa, amely sem a hengeralkotón, sem a fedőlappal való metszésvonalon nincs rajta, éppen a kúp alkotójára esik; ez mutatja, hogy az ilyen beillesztésnek nincs akadálya, ebből a helyzetből eleresztve a gömb lejjebb esik, vagyis még a fedőlap szintjét sem éri el a legmagasabb pontja.

3. feladat. Bizonyítsuk be, hogy a hegyesszögű háromszög területe egyenlő a köréje írható kör sugarának és a magasságvonalak talppontjai által meghatározott háromszög fél kerületének szorzatával.

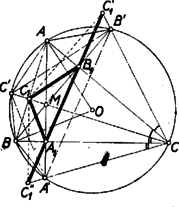
I. megoldás: Legyenek az

A B C

hegyesszögű háromszög magasságvonalainak talppontjai rendre

A_{1}

B_{1}

C_{1}

. Ezek belső pontjai a

B C

C A

, ill.

A B

szakasznak. Ismeretes, hogy hegyesszögű háromszögben az oldalak felezik a talpponti háromszög külső szögeit.

Ennélfogva ha

C_{1}

-nek

C A

, ill.

C B

-re vonatkozó tükörképe

C'_{1}

, ill.

C''_{1}

, akkor a

B_{1} C_{1}

ill.

A_{1} C_{1}

oldalnak

B_{1} C'_{1}

, ill.

A_{1} C''_{1}

tükörképe a

B_{1} A_{1}

oldalnak

B_{1}

, ill.

A_{1}

-en túl való meghosszabbítására esik, tehát

C'_{1} C''_{1}

a talpponti háromszög

k

kerületével egyenlő. Továbbá a tükrözés folytán a

C'_{1} C C''_{1}

háromszög egyenlő szárú:

C C'_{1} = C C_{1} = C C''_{1} = m_{c}

, és

C

-nél levő szöge kétszerese az

A C B

hegyes szögnek. ‐ Az

A B C

háromszög körülírt körének

O

középpontja az

A

B

csúcsokkal együtt a

C' C C''_{1}

-höz hasonló háromszöget alkot, mert

O A = O B = r

, és

A O B ∢ = 2 \cdot A C B ∢

. A hasonlóság folytán:

C' C''_{1} : A B = C C'_{1} : O A

, másképpen

k : c = m_{c} : r

, és ebből

c m_{c} = r k

, ahol a bal oldal az eredeti háromszög

t

területének kétszerese. Így

t = r k / 2

, amit bizonyítanunk kellett.

Megjegyzés. Derékszögű háromszögben a talpponti háromszög elfajul, mert két csúcsa egybeesik a derékszög csúcsával, pl. ha

A C B ∢ = 90^{\circ}

, akkor

A_{1} \equiv B_{1} \equiv C

. Ha a

C C_{1}

szakaszt oda-vissza bejárva elfogadjuk, a ,,háromszög'' ,,kerületének'', akkor a tétel ez esetben is igaz, mert

k = 2 m_{c}

, másrészt

r = c / 2

, ennélfogva

k r / 2 = c m_{c} / 2 = t

.
A bizonyításban felhasznált hasonlóság tompaszögű háromszögben is fennáll ‐ éspedig akár hegyes szög van

C

-nél, akár tompa (természetesen bizonyítása kissé módosul), de a

C'_{1} C''_{1}

szakasz nem a talpponti háromszög

k

kerületét jelenti, hanem a

k - 2 h

különbséget, ahol

h

a talpponti háromszögnek az az oldala, amelynek végpontjai az eredeti háromszög hegyes szögeinek csúcsából húzott magasságok talppontjai. A módosulás magyarázata az, hogy ez esetben csak a leghosszabb oldal egyenese tartja meg a talpponti háromszögben külső szögfelezői szerepét, a másik kettőé belső szögfelezővé válik.

II. megoldás: Ismeretes, hogy a háromszög

M

magasságpontjának az oldalakra, más szóval az

A_{1}

B_{1}

C_{1}

magasságtalppontokra való

A'

B'

C'

tükörképei a körülírt kör kerületén vannak (

A'

C C''_{1}

egyenesen,

B'

C C'_{1}

-n). Így az

A' B' C'

háromszög az

A_{1} B_{1} C_{1}

talpponti háromszögnek az

M

középpontból

2

-szeresre nagyított képe ‐ mert (pl.)

A'

M A_{1}

egyenesen van ‐, és

M A_{1} = A_{1} A'

-ből

M A' = 2 M A_{1}

. Eszerint (pl.)

B' C' = 2 B_{1} C_{1}

. ‐ Hegyesszögű háromszögben az

M

belső pont, ezért tükörképei az

A

-t,

B

-t,

C

-t nem tartalmazó

B C

C A

, ill.

A B

ívre esnek. Az

A C' B A' C B'

(konvex) hatszög területe

2

-szerese az

A B C

háromszög

t

területének, mert annál az

A B C'

B C A'

C A B'

háromszögek együttes területével nagyobb, ez pedig egyenlő

t

-vel, mert tükörképeik:

A B M

B C M

C A M

éppen kitöltik

A B C

-t.
E hatszögnek az

A

B

C

csúcsokba befutó oldalpárjai egyenlők, mert pl.

C A' = C M = C B'

, tehát a körülírt kör

O A'

O B'

O C'

sugaraival való felbontással területét

3

deltoid területének összegeként is előállíthatjuk:

\begin{matrix} 2 t = \frac{O A \cdot B' C'}{2} + \frac{O B \cdot C' A'}{2} + \frac{O C \cdot A' B'}{2} = r B_{1} C_{1} + r C_{1} A_{1} + r A_{1} B_{1} = \\ = r (B_{1} C_{1} + C_{1} A_{1} + A_{1} B_{1}) = r k . \end{matrix}

Evvel igazoltuk a bizonyítandó állítást.

Megjegyzés. Derékszögű háromszögben

M \equiv C \equiv A' \equiv B'

, így a hatszög elfajul, tompaszögű háromszög esetén pedig hurkolttá válik.