Cím: Az 1958.évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Surányi János 
Füzet: 1959/március, 67 - 77. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. feladat. Legyen adva a síkban 6 pont, amelyek közül semelyik 3 sincs egy egyenesen. Bizonyítandó, hogy ezek közül kiválaszthatók egy olyan háromszög csúcsai, amelynek egy szöge legalább 120∘-os.
A feladat állítása a következővel egyértelmű: van olyan 3 pont, amelyek valamelyikéből a másik kettőn át húzott félegyenesek hajlásszöge legalább 120∘-os. Ebben a formában fogjuk bizonyítani az állítást.

 
I. megoldás. A következő segédtételből indulunk ki. Ha egy háromszög belsejében adva van egy P pont, akkor a P-ből a csúcsokhoz húzott egyenesek hajlásszögének valamelyike legalább 120∘-os. Valóban, véve a három szög legnagyobbikát (illetőleg az ilyenek egyikét), ennek a háromszorosa legalább akkora, mint a három szög összege, vagyis legalább 360∘, ez a szög tehát legalább 120∘-os.
Ebből következik, hogy a feladat állítása teljesül minden olyan esetben, amelyben kiválaszthatók az adott pontok közül egy háromszög csúcsai úgy, hogy ez a háromszög tartalmazzon adott pontot.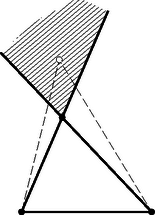
 
 

1. ábra
 

Válasszunk ki most már az adott 6 pont közül hármat. Ha abban a háromszögben amelynek ezek a csúcsai, van még adott pont, akkor, mint láttuk, teljesül a feladat állítása; de teljesül akkor is, ha a háromszög két oldalának a közös csúcsukon túli meghosszabbításai közt levő szögtartományba esik adott pont (1. ábra), mert akkor a kérdéses csúcsot tartalmazza az a háromszög, amelyet a másik két csúcs és a negyedik pont határoz meg. A síkot a háromszög oldalegyeneseivel felosztva feltehetjük tehát, hogy a további adott pontok a háromszög oldalaihoz csatlakozó síkrészekben helyezkednek el. Hozzávéve közülük egyet a már kiválasztottakhoz, a tekintetbe vett pontok egy konvex négyszög csúcsai (2. ábra).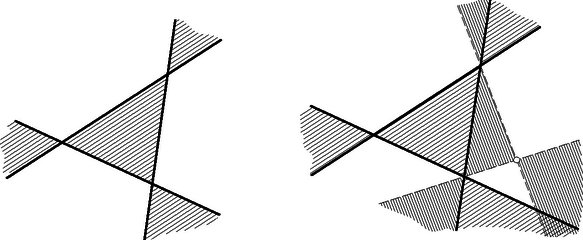
 
 

2. ábra
 

Meghúzva a négyszög még hiányzó két oldalának egyenesét, ismét feltehetjük, hogy sem a keletkező új háromszögbe, sem pedig az oldalmeghosszabbítások közti szögtartományokba nem esik adott pont. Így véve egy ötödik pontot az az előzőkkel konvex ötszöget alkot, és a gondolatmenetet még egyszer megismételve nyerjük, hogy elég azt az esetet megvizsgálni, amelyben az adott pontok egy konvex hatszög csúcsai. Ebben az esetben a hatszög legnagyobb szögének, vagy a legnagyobbak egyikének a hatszorosa legalább akkora, mint a hat szög összege, tehát legalább 720∘, s így a szög legalább 120∘-os. Ezzel igazoltuk a feladat állítását.
 
II. megoldás. Az adott pontok vagy egy konvex hatszög csúcsai, vagy közülük 3, 4 vagy 5 egy olyan konvex sokszög csúcsait alkotja, amely tartalmazza a többi adott pontot. Az így kapott hat‐, ill. három‐, négy‐ vagy ötszöget az adott pontok konvex burkának nevezzük.1
Ha a konvex burok hatszög, akkor, mint az előző megoldás végén láttuk, egyik szöge legalább 120∘-os.
Ha a konvex burok négy‐, vagy ötszög, akkor egyik átlójával, ill. egyik csúcsából induló átlóival háromszögekre bontjuk. A keletkező háromszögek valamelyike tartalmaz adott pontot. A hátralevő esetek mindegyikében találunk tehát olyan háromszöget, amelynek a csúcsai adott pontok és amely tartalmaz ezeken kívül is adott pontot. Az előző megoldás elején láttuk, hogy ekkor a csúcsokat a további adott ponttal összekötő szakaszok közti szögek valamelyike legalább 120∘-os. Ezzel igazoltuk a feladat állítását.
 
Megjegyzések. a) Nem lényeges annak kikötése, hogy semelyik 3 pont sincs egy egyenesen, ha ugyanis 3 pont egy egyenesen van, akkor a középsőből a két szélsőhöz húzott félegyenesek 180∘-os (tehát 120∘-nál nagyobb) szöget zárnak be.
b) Vizsgáljuk meg, előfordulhat-e, hogy az adott pontok mindegyikét minden lehető módon összekötve két-két másikkal, a keletkező forgásszögek legnagyobbika sem nagyobb 120∘-nál, és ha igen, milyen esetekben következik ez be. A bizonyításból azonnal adódik, hogyha a 6 pont konvex burka hatszög, akkor a kérdéses legnagyobb szög akkor 120∘-os, ha a hatszög minden szöge egyenlő, vagyis, ha az oldalai rendre párhuzamosak egy szabályos hatszög oldalaival (nem kell azonban szabályosnak lennie a hatszögnek, mint azt több versenyző állította).
Ha az adott pontok konvex burka nem hatszög, akkor láttuk, hogy kiválaszthatók a pontok közül egy olyan háromszög csúcsai, amely tartalmaz legalább még egy adott P pontot. A bizonyításból világos az is, hogy P-ből a háromszög oldalainak 120∘-os szögben kell látszaniuk, mert különben valamelyik biztosan 120∘-nál nagyobb szög alatt látszik.
 
 

3. ábra
 

Ha teljesül is ez a feltétel, akkor is fellép 120∘-nál nagyobb szög, amint legalább még egy Q pont van adva (3. ábra). Ha ugyanis Q a P-ből a csúcsokhoz mutató félegyenesek valamelyikén van, akkor arra 3 pont esik, és így van 180∘-os szög is. Ha pedig Q az említett félegyenesek közti 120∘-os szögtartományok belsejében van, akkor a P-ből Q-n át húzott félegyenes a szögtéren kívül levő félegyenessel 120∘-nál nagyobb szöget zár be. Ezzel bebizonyítottuk a következőt: hat adott pont mindegyikéből minden két-két ponthoz húzott félegyenes-párok közötti szögek legnagyobbika legalább akkora, mint a szabályos hatszög egy szöge, és csak abban az esetben pontosan akkora, ha az adott pontok egy olyan konvex hatszög csúcsai, amelynek az oldalai párhuzamosak egy szabályos hatszög oldalaival.
c) A most kimondott állítás 6 helyett 3, 4 vagy 5 pont esetére is igaz. Ha ugyanis mindegyik pont csúcsa a pontrendszer konvex burkának, akkor a sokszög legnagyobb szöge legalább akkora, mint a szabályos három‐, négy‐, ill. ötszög egy szöge, és pontosan ekkora csak úgy lehet, ha a sokszög minden szöge ekkora, vagyis ha oldalai párhuzamosak egy ugyanennyi oldalú szabályos sokszög oldalaival. Ha pedig (4 vagy 5 adott pont esetén) van olyan pont, amelyik nem csúcsa a konvex buroknak, akkor egy ilyen pont körül, mint már láttuk, fellép legalább 120∘-os szög, viszont a szabályos négy‐ és ötszög egy szöge kisebb 120∘-nál.
Megmutatjuk, hogy a most belátott szabályosság 7 adott pont esetén már nem áll fenn: a síkban 7 pont közül valamelyiket össze tudjuk kötni két másikkal úgy, hogy 120∘-nál nagyobb szög keletkezzék, viszont bárhogy adunk meg egy 120∘-nál nagyobb szöget, mindig megadható 7 pont úgy, hogy a köztük fellépő összes szögek kisebbek legyenek az adott szögnél. Hozzátesszük, hogy az utoljára említett pontrendszerek már nem lesznek általában konvex 7-szög csúcsai.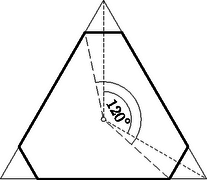
 
 

4. ábra
 

Ha a 7 pont konvex burka 7-nél kevesebb oldalú, akkor az állítás első része következik a b) pontban bizonyított állításból. Ha pedig az adott pontok egy konvex 7-szög csúcsai, akkor ennek legnagyobb szöge legalább akkora, mint a szabályos 7-szög egy szöge, ez pedig nagyobb mint 120∘. Az állítás második felének igazolására vágjuk le egy szabályos háromszög csúcsait a csúcsokhoz közel a szemközti oldallal párhuzamos egyenessel, és az így keletkező hatszög csúcsaihoz vegyük hozzá a háromszög középpontját (4. ábra). Ekkor könnyen beláthatjuk, hegy a fellépő legnagyobb szög is tetszés szerint közel lesz 120∘-hoz.
d) Az elmondott eredmények L. M. Blumenthal amerikai matematikustól származnak.2 Ő vetette fel általában a kérdést, hogy milyen alsó korlátot lehet megadni tetszés szerinti n pont esetén a fellépő legnagyobb szögre. Szekeres György megmutatta,3 hogy ha a pontok egy síkban vannak és számuk 2k (k természetes szám), akkor az (1-1k)180∘-os szög játszik hasonló szerepet, mint 7 pont esetén a 120∘, és térben is nyert hasonló eredményeket. Még síkban sincs azonban minden n-re megoldva a probléma.
 
2. feladat. Bizonyítsuk be, hogyha u és v olyan egész számok, amelyekre
u2+uv+v2
osztható 9-cel, akkor u is, v is osztható 3-mal.
Számba véve u és v lehetséges maradékait 3-mal való osztásnál, véges sok esetet kapunk, és ezek végigpróbálásával nyerhető a feladat egy megoldása. A versenyzők nagy része ezt az utat választotta, többen még a kifejezés szimmetriáját sem használva ki. Könnyen célhoz érhetünk azonban egy algebrai átalakítás segítségével:
 
Megoldás. Alakítsuk át a kifejezést a következőképpen:
u2+uv+v2=(u-v)2+3uv.
A kifejezés osztható 9-cel, tehát 3-mal is, és mivel a jobb oldal második tagja is osztható vele, tehát az első: (u-v)2 is osztható 3-mal.
Egy négyzetszám csak úgy lehet 3-mal osztható, ha az alap ‐ esetünkben u-v ‐ osztható 3-mal, és ekkor a négyzete 9-cel is osztható.
Mivel az egész kifejezés is osztható 9-cel, így a második tag, 3uv is osztható 9-cel, tehát uv osztható 3-mal. Ez csak úgy lehet, ha valamelyik tényező is osztható 3-mal. Beláttuk azonban, hogy a különbségük is osztható 3-mal, ez pedig csak úgy lehet, ha mind a kettő: u is, v is osztható 3-mal, és ezt kellett bizonyítanunk. (Világos megfordítva, hogyha ez teljesül, akkor a kifejezés valóban osztható 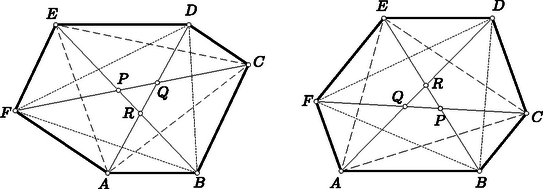9-cel.)
 
3. feladat. Az ABCDEF konvex hatszögben az AB és DE, a BC és EF, továbbá a CD és FA oldalak párhuzamosak. Bizonyítsuk be, hogy az ACE és BDF háromszögek területe egyenlő.
 
I. megoldás. Húzzuk meg az AD, BE és CF átlókat, metszéspontjaik legyenek R, P, Q (ezek egybe is eshetnek). Ezekkel az ACE, illetőleg a BDF háromszöget a következő háromszögekre bontottuk szét (5. ábra):
ACQ,CEP,EAR,PQR,(1)DFQ,FBP,BDR,PQR.

 
 

5. ábra
 

A feladat állításának bizonyításához elegendő azt megmutatni, hogy itt az egymás alatt álló háromszögek területe egyenlő. Ez az utolsó párra nyilvánvaló. Az első párra ez abból következik, hogy az ACF és ADF háromszögek egyenlő területűek, mert AF oldaluk közös és a rá merőleges magasság AF és CD párhuzamossága folytán egyenlő. Ezekből elhagyva közös részüket, az AQF háromszöget, a maradó ACQ és DFQ háromszögek is egyenlő területűek. Ugyanígy látható be a további két-két háromszög területének egyenlősége is. Ezzel a feladat állítását igazoltuk.
 
Megjegyzés. A megoldás épít arra a szemléletes tényre, hogy az (1) alatti háromszögek az ACE, ill. BDF háromszöget töltik ki hézagtalanul és egyrétűen. Ez azonban a szemléletre való hivatkozás nélkül is belátható.
A meghúzott AD, BE és CF átlók egyenese átmetszi az ACE és BDF háromszögeket, mert a hatszög konvex volta miatt az AD egyenesnek pl. a B és C csúcsok az egyik oldalán, az E és F csúcsok az ellenkező oldalán vannak, s így metszi az egyenes a CE és FB szakaszt, tehát az említett háromszögeket is. Ezeknek az átlóknak a metszéspontjai is az említett háromszögekben vannak, mert véve valamelyik átlón az egyik háromszögnek az átlóra eső csúcsát és a szemközti oldallal való metszéspontot, ezeket is elválasztja a másik két átló.
Ha a három átló egy ponton megy keresztül, akkor nincs mit bizonyítanunk tovább. Ellenkező esetben pl. az A, C, E csúcsok a PQR háromszög QR, PQ, RP oldalainak meghosszabbításain vannak. Nem lehet pl. az A csúcs az RQ oldal Q-n túli és ugyanakkor az E csúcs az RP oldal P-n túli meghosszabbításán, mert akkor a PQR háromszög a PQ oldal ellenkező oldalán lenne, mint az ACE háromszög, nem lehetne tehát az előbbi háromszög az utóbbiban. Így A, C, EQR-nek az R-en túli, PQ-nak Q-n, ill. RP-nek P-n túli meghosszabbításán van, vagy mindegyik a megfelelő oldal ellenkező irányú meghosszabbításán (5. ábra). Ebből pedig következik bizonyítandó állításunk. Hasonló meggondolás érvényes a BDF háromszögre is.
 
 

6. ábra
 

A bizonyított állítást így fogalmazhatjuk: Egy háromszög csúcsain át húzzunk a háromszöget metsző egyeneseket és tekintsük az ezek közti háromszöget, ‐ ha a három egyenes nem megy át egy ponton. Ekkor az első háromszög csúcsai az utóbbi három oldalának három különböző csúcsból induló meghosszabbításain vannak (6. ábra, az első háromszög csúcsai üres, az utóbbiéi tele köröcskékkel vannak jelölve).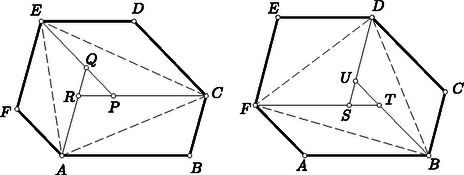
 
II. megoldás. Egészítsük ki paralelogrammává egyrészt a hatszög AB és BC, CD és DE, továbbá EF és FA oldalát, másrészt a BC és CD, DE és EF, FA és AB oldalpárokat. A paralelogrammák negyedik csúcsait jelöljük R, P, Q-val, ill. U, S, T-vel. (A három-három pont egybe is eshet.) A paralelogrammáknak két-két hatszögcsúcsot összekötő átlói az ACE, ill. a BDF háromszög oldalai (7. ábra).
 
 

7. ábra
 

Mind a két paralelogramma-rendszerben két-két paralelogrammának a közös csúcsból induló oldalegyenese egybeesik, mivel párhuzamosak a hatszögnek azok az oldalai, amelyekkel a szóban forgó paralelogrammaoldalak párhuzamosak.Így a PQR és az STU háromszögek oldalai (ha a három pont nem esik egybe) két-két hatszögoldallal párhuzamosak, és hosszuk a párhuzamos hatszögoldalak hosszának a különbsége. A két háromszög tehát egybevágó. Ebből következik, hogy a három-három paralelogramma területösszege egyenlő. Ennek folytán az ACE háromszög területe is, a BDF-é is a megfelelő három paralelogramma fél területének és a köztük levő háromszög területének az összege, s így a kettő egyenlő.
 
Megjegyzések. a) A bizonyítás ismét szigorúbbá tehető azzal, ha megmutatjuk, hogy a három-három félparalelogramma és az ezek oldalai között keletkező háromszög hézagtalanul és egyrétűen töltik ki az ACE, ill. BDF háromszöget. Itt pl. az ACE háromszöget az AQ, CR, EP egyenesekkel osztottuk részekre. Ezek az egyenesek átmetszik a háromszögeket, mert pl. AQ párhuzamos BC-vel és EF-fel, és az utóbbi két egyenes AQ ellenkező oldalára esik a hatszög konvex volta miatt. Hasonlóan okoskodhatunk a többi egyenesekre, továbbá a BDF háromszögre. Ekkor azonban a keletkezett ábrákra is érvényes az előző megoldáshoz fűzött megjegyzés utolsó megállapítása, abból pedig következik a bizonyítandó állítás.
b) A bizonyítás azt adja, hogy a feladatban szereplő háromszögek területe a hatszög és a PQR (ill. a vele egybevágó STU) háromszög területének számtani közepe, hogy tehát az ACE és BDF háromszögek területe legalább akkora, mint a hatszög területének a fele. Ebből egyszersmind következik, hogy a szomszédos oldalpárok alkotta háromszögek közül legalább az egyik területe nem nagyobb a hatszög területének hatodrészénél. (Sőt ez az ABC, CDE, EFA, továbbá a BCD, DEF, FAB háromszögek közül legalább egy-egyre teljesül.) Felvetődik az a kérdés, hogy nem érvényes-e a második állítás minden konvex hatszögre. A kérdésre egyelőre nem ismeretes a válasz.
 
III. megoldás. Ha pl. az AB és DE oldalak egyenlők, akkor az ABDE négyszög paralelogramma és így az AEF és DBC háromszögek megfelelő oldalai párhuzamosak, továbbá AE és DB egyenlősége folytán egyenlők is, tehát a hatszög párhuzamos oldalai egyenlők is (8.ábra). Ebből az AE és DB oldalak egyenlőségéhez hasonlóan következik, hogy az ACE és DFB háromszög megfelelő oldalai egyenlők, tehát a két háromszög egybevágó.
 
 

8. ábra
 

Ha a szemközti oldalak különböző hosszúságúak, akkor vizsgáljuk meg, hogyan változik a feladatban szereplő háromszögek területe, ha pl. az AB oldalt eltoljuk, irányát megtartva, a hatszöggel ellenkező oldalra, de úgy, hogy ne érje el az AF és BC egyenesek metszéspontját. Az eltolt oldal legyen A1B1. Az ACE háromszög ugyanannyival változik, mint a változatlanul maradó CDE háromszög hozzácsatolásával keletkező ACDE négyszög (9. ábra). Ezt az AD átlóval kettévágva az ACD és ADE háromszögek területének változását vizsgáljuk. Az ACD és A1CD háromszög területe egyenlő, mert AA1‖CD. Jelöljük másrészt AB és A1E metszéspontját A2-vel, akkor az ADE és az A2DE háromszög területe egyenlő, mert AA2‖DE. Így az ACDE négyszög ‐ és vele együtt az ACE háromszög ‐ területe az A1DE és A2DE háromszög területének különbségével, vagyis az A1DA2 háromszög területével nő. Ugyanígy látható ‐ AB és B1D metszéspontját B2-vel jelölve ‐, hogy a BDF háromszög területe a B1EB2 háromszög területével nő.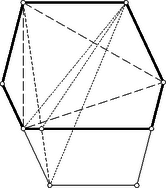
 
 

9. ábra
 

Az A1DA2 és B1EB2 háromszögek azonban egyenlő területűek (10. ábra), mert úgy származtathatók, hogy az A1DE háromszögből A2DE-t, ill. B1DE-ből B2DE-t elhagyjuk, és itt a kisebbítendők A1B1‖DE folytán, a kivonandók pedig A2B2‖DE folytán egyenlők. Az ACE és BDF háromszög területe tehát ugyanannyival változik.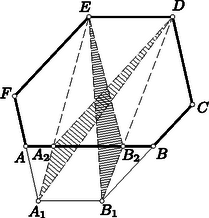
 
 

10. ábra
 

Tegyük most fel, hogy AB>DE (ellenkező esetben AB és DE szerepét felcseréljük). Úgy mozdítsuk el AB-t, hogy A1B1=DE legyen. Ekkor tudjuk, hogy A1CE és B1DF egyenlő területű, ACE és BDF pedig ezektől egyenlő területekkel különböznek, tehát szintén egyenlő területűek. Ezt kellett bizonyítanunk.
 
IV. megoldás. Egészítsük ki a hatszöget az AB, CD, EF oldalak meghosszabbításával egy PQR háromszöggé (11. ábra). Ezt a háromszöget és a területét is jelöljük T-vel. A hatszöget T-ből a hozzá hasonló PED, FQA és CBR háromszögek levágásával kapjuk. Ezekben az oldalak legyenek T oldalainak; λ-szorosai, μ-szörösei, ill. ν-szörösei.
 
 

11. ábra
 

Az ACE háromszöget T-ből az ARC, CPE és EQA háromszögek lemetszésével kapjuk. Az elsőnek AR oldala a QR oldal 1-μ-szöröse, magassága pedig ‐ mint a CBR háromszög C-ből húzott magassága ‐ a T háromszög P-ből QR-re bocsátott magasságának ν-szöröse. Így a háromszög területe (1-μ)νT. Hasonlóan számítva a másik két háromszög területét is a következő területegyenlőséget kapjuk:
ACE=T-(1-μ)νT-(1-ν)λT-(1-λ)μT==T(1-λ-μ-ν+λμ+μν+νλ).


A BDF háromszögre hasonlóan számolva azt nyerjük, hogy
BDF=T-(1-λ)νT-(1-μ)λT-(1-ν)μT==T(1-λ-μ-ν+λμ+μν+νλ),


tehát
ACE=BDF.

 
V. megoldás. A feladat megoldása nem igényel különösebb ötletet, ha koordinátageometriát alkalmazunk. Válasszuk meg a koordinátatengelyeket úgy, hogy az y-tengely ne legyen párhuzamos a hatszög egyik oldalával sem. Ekkor az oldalak iránytangense létezik. Az A, B, C, D, E, F pontok koordinátáit jelöljük sorra (x1,y1),...,(x6,y6)-tal.
Azt tudjuk, a szemközti oldalpárok párhuzamosak, tehát iránytangenseik különbsége 0:
y1-y6x1-x6-y4-y3x4-x3=y3-y2x3-x2-y6-y5x6-x5=y5-y4x5-x4-y2-y1x2-x1=0.
Ez csak úgy lehet, ha közös nevezőre hozás után a számlálók értéke, és így ezek összege is 0. Rendezzük ezt az összeget az x-ek szerint:
0=(x4-x3)(y1-y6)-(x1-x6)(y4-y3)+(x6-x5)(y3-y2)--(x3-x2)(y6-y5)+(x2-x1)(y5-y4)-(x5-x4)(y2-y1)==x1(y3-y5)+x2(y6-y4)+x3(-y1+y5)+x4(-y6+y2)++x5(-y3+y1)+x6(y4-y2).


A maradó első, harmadik és ötödik tag összege az ACE háromszög kétszeres területét adja, a második, negyedik és hatodik pedig negatív előjellel a BDF háromszög kétszeres területét. A két háromszög területe tehát egyenlő, és ezt kellett bizonyítanunk.
 
 

12. ábra
 

 
Megjegyzés. Figyeljük meg, hogy a bizonyítás egyedül a szemközti oldalak párhuzamosságát használja fel, tehát a hatszög konvex voltát nem, sőt még akkor is helyes marad, ha az oldalak egymást (a csúcsoktól különböző pontokban) átmetszik. (Néhány ilyen hatszöget mutat a 12. ábra.) Másrészt a háromszögek területét a használt képlet előjellel adja, tehát a bizonyítás azt is adja, hogy az ACE és BDF háromszögek körüljárása is mindig megegyezik. Erre az általánosabb állításra adunk most egy koordinátákat nem használó bizonyítást is.
 
VI. megoldás. Egy ABC háromszög területét tekintsük pozitívnak vagy negatívnak aszerint, amint a háromszöget a csúcsok megadott sorrendje szerint körüljárva az óra járásával ellentétes vagy azzal egyező irányban haladunk.
 
 

13. ábra
 

Könnyen látható, hogy az ABC háromszög síkjának egy tetszés szerinti O pontjára (13. ábra) ‐ háromszögek előjeles területét ugyanúgy jelölve, mint magát a háromszöget ‐ fennáll a következő összefüggés:
ABC=OAB+OBC+OCA.(2)

Ha valamelyik három pont egy egyenesre esik, akkor a keletkező egyenesszakasszá fajult ,,háromszög'' területén természetesen 0-t értünk. Ezt felhasználva választunk az adott hatszög síkjában egy O pontot, és minden háromszöget olyan háromszögekből teszünk össze, amelyeknek egyik csúcsa O.
Előjeles területekre is igaz, hogy ha az ABC és ABD háromszögek C és D csúcsát összekötő egyenes párhuzamos az AB oldallal, akkor a két háromszög területe egyenlő, mert az abszolút értékekről tudjuk ezt, de a körüljárás sem változhat meg, ha egy csúcsot a szemközti oldallal párhuzamosan mozdítunk el.
Ha tehát ABCDEF egy olyan hatszög, amelyben AB‖DE, BC‖EF és CD‖FA, akkor az ABE és ABD, a CDA és CDF és az EFC és EFB háromszögek területe egyenlő, tehát (2)-t alkalmazva
OAB+OBE+OEA=OAB+OBD+ODA,OCD+ODA+OAC=OCD+ODF+OFC,OEF+OFC+OCE=OEF+OFB+OBE.
Itt az első oszlopban a jobb és bal oldalon ugyanazok a háromszögek állnak, a bal második oszlopban pedig azok, mint a jobb harmadik oszlopban, csak más sorrendben. Így a három egyenlőséget összeadva és az egyenlő tagokat a két oldalon elhagyva azt kapjuk, hogy
OEA+OAC+OCE=OBD+ODF+OFB,
amiből (2) alapján
EAC=BDF,
és ezt akartuk bizonyítani.
 
VII. megoldás. Megoldható a feladat vektorok segítségével is. Ehhez a vektorok vektoriális szorzatát fogjuk felhasználni és annak következő tulajdonságait.4
Az r és s vektorok vektoriális szorzatán ‐ amit r×s-sel jelölünk ‐ azt a vektort értjük, amelynek hossza az r és s vektorokból alkotható paralelogramma területének a mérőszámával egyenlő, amely merőleges az r és s síkjára és annak arra az oldalára mutat, amelyikről nézve r-t pozitív (az óramutató járásával ellentétes) irányban lehet 180∘-nál kisebb szöggel s-re ráforgatni.
Párhuzamos vektorok vektoriális szorzata 0-vektort ad.
Egy vektoriális szorzat két tényezőjét felcserélve a szorzat előjelet vált.
A vektoriális szorzatra érvényes a disztributív tulajdonság, vagyis bármely három r, s, t vektorra fennállnak az
r×(s+t)=r×s+r×t és (s+t)×r=s×r+t×r  
azonosságok.
 
 

14. ábra
 

Ezeket felhasználva azt fogjuk bebizonyítani, hogy a hatszögből az ACE háromszög oldalai által lemetszett háromszögek területösszege és a BDF háromszög oldalaival lemetszetteké egyenlő. A 14. ábrán feltüntetett jelöléseket használva az előbbi összeg kétszeresét az
a×b1+b×c1+c×a1   
vektor képviseli, az utóbbi kétszeresét pedig a
c1×a+a1×b+b1×c  
összeg. Ha a hatszög konvex, akkor mind a hat vektor a síkjának ugyanarra az oldalára mutat. Ezek különbségéről kell belátnunk, hogy az 0.
A különbséget úgy fogjuk képezni, hogy a második sor összeadandóinak a tényezőit felcseréljük. Ha még ehhez az összeghez a×a1+b×b1+c×c1-et adunk, ezzel az összeg értékét nem változtattuk meg, mert párhuzamos vektorok szorzatait adtuk hozzá. Elegendő tehát a következő kifejezésről megmutatni, hogy a 0-vektorral egyenlő:
a×b1+b×c1+c×a1+a×c1+b×a1+c×b1+a×a1++b×b1+c×c1=(a+b+c)×(a1+b1+c1).  


Azonban zárt hatszögről lévén szó
a+b+c+a1+b1+c1=0,  
vagyis az első három vektor összege a második hároménak negatívja, azzal tehát párhuzamos, és így vektori szorzatuk 0. Ezt kellett bizonyítanunk.
 
Megjegyzés. Ennél a megoldásnál látszólag ismét kihasználtuk a hatszög konvex voltát. Belátható azonban, hogy előjeles területtel számolva minden hatszögnek (és minden zárt sokszögnek) tulajdoníthatunk területet, az ABCDEF hatszögnek pl. az ABC+ACD+ADE+AEF területösszeget. Ez nem változik meg azáltal, ha A helyett egy másik csúcsból kiinduló átlóival bontjuk háromszögekre a hatszöget. Az ACE háromszöget az ABC, CDE, EFA háromszögek (előjeles) területei a hatszög így értelmezett területére ,,egészítik ki'', és hasonlóan BDF-et a BCD, DEF, FAB háromszögek. Végül a felírt vektori szorzatok tetszőleges hatszög esetén a megfelelő háromszögek előjeles területeit képviselik. Ezek végiggondolásával adódik, hogy az utolsó bizonyítás is kiadja az állítást bármilyen hatszögre, amelynek a szemközti oldalai párhuzamosak.
1Képzeljünk a pontokban a síkra merőlegesen gombostűket betűzve és vegyük körül ezeket cérnával, majd húzzuk össze a cérnát a legrövidebbre, ekkor a cérna megadja a konvex burkot.

2Journal of the American Mathematical Society, 61, (1939), 912‐922. o.

3Ugyanott, 63, (1941), 208‐210. o.

4Lásd pl. Feldmann L., Vektoralgebra (Középiskolai szakköri füzet) 20‐27. o.