Kezdőlap


Cím:	Négyzetekkel burkolt konvex alakzatok (2. közlemény)
Szerző(k):	Kárteszi Ferenc
Füzet:	1959/február, 33 - 37. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek
Hivatkozás(ok):	Feladatok: 1959/március: 965. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(2. közlemény)^{$^{*}$}

4. Az összegtartományra vonatkozó tételek

Az összegtartomány fogalmának hasznosítását a felvetett problémára az itt következő két tételnek köszönhetjük.
I. TÉTEL. Két korlátos konvex alakzatnak az összege is korlátos konvex alakzat.
BIZONYÍTÁS. Az állításnak a korlátosságra vonatkozó részét bizonyítandó, állapítsuk meg, hogy két körtartománynak az összege miféle alakzat. A 8. ábrával kísért meggondolásokra támaszkodva azonnal belátható, hogy egy

R

és egy

r

sugarú kör összege egy

R + r

sugarú kör. Ha a

K

és

L

körtartományok sugara rendre

R

és

r

, továbbá, ha egy

O

kezdőpont felhasználásával az

M

összegtartomány adódik, akkor világos, hogy a

K

egy belső

X

pontjának és az

L

egy belső

Y

pontjának megfelelő

Z

összegpont az

M

tartománynak belső pontja. Ha már most

A

és

B

K

, illetve az

L

tartomány belsejében helyezkedik el, akkor az

O

-val szerkesztett

A + B = C

tartomány, éppen az

X

Y

Z

pontokra vonatkozó megállapítás szerint, az

M

tartomány belsejében helyezkedik el, vagyis valóban korlátos.
A tétel másik része azt állítja, hogy

A

-val és

B

-vel együtt

A + B = C

is konvex. Ezt bizonyítandó csak azt kell igazolni, hogy

C

tetszőleges

Z_{1}

és

Z_{2}

pontjaival együtt a

Z_{1} Z_{2}

szakasz bármely

Z

pontja is

C

-hez tartozik.
Legyen az

A

és

B

tartományok olyan két-két pontja az

X_{1}

K_{2}

és

Y_{1}

Y_{2}

, amelyekre nézve érvényesek az

O

kezdőpontra vonatkozó

\begin{matrix} \vec{O X_{1}} + \vec{O Y_{1}} & = \vec{O Z_{1}}, \\ \vec{O X_{2}} + \vec{O Y_{2}} & = \vec{O Z_{2}} \end{matrix}

relációk.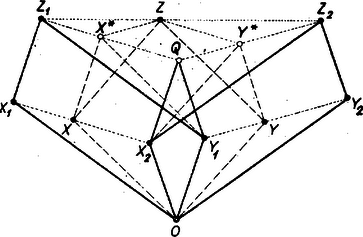

9. ábra

A 9. ábra

O X_{1} Z_{1} Y_{1}

és

O X_{2} Z_{2} Y_{2}

vektorparalelogrammáival származtattuk a

Z_{1}

és

Z_{2}

összegpontokat. Az ábra

Q

pontját az

O X_{2} Q Y_{1}

vektorparalelogramma szolgáltatja, tehát

\begin{matrix} \vec{O X_{2}} + \vec{O Y_{1}} = \vec{O Q} . \end{matrix}

(Az összegeket realizáló átlók az ábrán nincsenek megrajzolva.)
Az

X_{1} X_{2}

és

Y_{1} Y_{2}

szakaszokon úgy választottuk az

X

és

Y

pontokat, hogy azok osztóviszonya egy előírt

λ

érték legyen:

\begin{matrix} X_{1} X : X X_{2} = Y_{1} Y : Y Y_{2} = λ (λ > 0) . \end{matrix}

A mondott paralelogrammák párhuzamos oldalait tekintve azonnal belátható, hogy az

O Y_{1} Y Y_{2}

alakzatot az

\vec{O X_{2}}

vektornak megfelelő eltolás

X_{2} Q Y^{*} Z_{2}

-be és az

O X_{1} X X_{2}

alakzatot az

\vec{O Y_{1}}

vektornak megfelelő eltolás

Y_{1} Z_{1} X^{*} Q

-ba viszi át. Ebből az is nyilvánvaló, hogy

\begin{matrix} Z_{1} X^{*} : X^{*} Q = Q Y^{*} : Y^{*} Z_{2} = λ . \end{matrix}

Innen pedig a

Z_{1} Q Z_{2}

háromszög

Z_{1} Z_{2}

oldalának

\begin{matrix} Z_{1} Z : Z Z_{2} = λ \end{matrix}

osztóviszonnyal definiált

Z

pontjára nézve nyomban belátható, hogy az

X^{*}

Q

Y^{*}

pontokkal együtt egy paralelogrammát létesít.
Minthogy

X X^{*}

párhuzamos és egyenlő

X_{2} Q

-val, ez pedig

O Y_{1}

-gyel, továbbá

X^{*} Z

párhuzamos és egyenlő

Q Y^{*}

-gal, ez pedig

Y_{1} Y

-nal, következésképpen az

X X^{*} Z

X_{2} Q Y^{*}

és

O Y_{1} Y

háromszögek egyező állású egybevágó háromszögek. Ebből már látható, hogy az

X Z

oldal is párhuzamos és egyenlő az

X_{2} Y^{*}

és

O Y

oldalakkal. Hasonló módon látható be, hogy

Y Z

párhuzamos és egyenlő

O X

-szel. Tehát az

O X Z Y

idom: paralelogramma. Ebből pedig

\begin{matrix} \vec{O X} + \vec{O Y} = \vec{O Z} \end{matrix}

már következik, vagyis a

Z_{1} Z_{2}

szakasz

λ

osztóviszonynak megfelelő

Z

pontja valóban

C

-hez tartozik. Hogyha

0

-tól fogva folyton és minden határon túl növekedik a

λ

értéke, akkor az

X

Y

és

Z

pontok rendre leírják az

X_{1} X_{2}

Y_{1} Y_{2}

és

Z_{1} Z_{2}

szakaszokat. Ezzel be is fejeztük a bizonyítást.

II. TÉTEL. Négyzetekkel burkolt konvex alakzatok összege is négyzetekkel burkolt konvex alakzat.
A tételt két tartományból képezett összeg esetén bizonyítjuk. (A tetszőleges számú összeadandó esetét, az itt közöltek alapján, az olvasó is könnyen elintézheti.)

BIZONYÍTÁS. Támaszkodni fogunk a következő állításra, melynek helyes volta a 8. ábrával kapcsolatos fejtegetések alapján azonnal belátható. Ha az

M

és

N

négyzetek állása megegyezik, akkor az

M + N = S

összegtartomány is egy ugyanolyan állású négyzet; ha e négyzetek oldalhossza rendre

m

n

és

s

, akkor

m + n = s

.
Legyenek

A

és

B

négyzetekkel burkolt konvex alakzatok, s legyen a

B

tartomány egy tetszőleges támasznégyzete

M

, az

N

pedig

A

-nak

M

-mel megegyező állású támasznégyzete (10. ábra).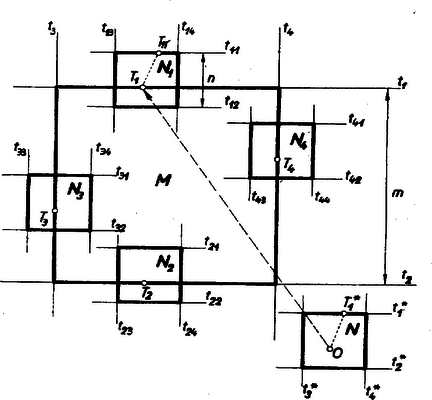

10. ábra

Legyen az

A + B = C

összegtartomány előállításához használt

O

kezdőpont

A

-nak (következésképpen

N

-nek is) egy belső pontja. Világos, hogy az

O

kezdőpont használatával szerkesztett

M + N = S

összegnégyzet a

C

összegtartományt magában foglalja. Ennél több is igaz:

S

C

tartománynak támasznégyzete. A támasznégyzet fogalmából ugyanis következik, hogy az

M

támasznégyzet

t_{k}

oldalán a

B

tartománynak legalább egy pontja van, legyen egy ilyen a

T_{k}

pont. Hasonlóan az

N

támasznégyzet

t_{k}^{*}

oldalán az

A

tartománynak legalább egy pontja van, legyen egy ilyen a

T_{k}^{*}

pont. A

T_{k} + A = A_{k}

összegtartomány az

A

tartománynak azzal az eltolásával áll elő, amely

O

-t a

T_{k}

pontba viszi. Ez az eltolás

O

-nál fogva magával viszi az

A

támasznégyzetét is

N_{k}

-ba, az

A_{k}

támasznégyzetébe. A

t_{k}

támaszegyenesnek

M

-mel ellentett oldalán

B

-nek nincs pontja,

A_{k}

-nak viszont legalább egy pontja van, mert

O

belső pontja

A

-nak; éspedig ilyen az

N_{k}

támasznégyzet

t_{k k}

támaszegyenesének az a

T_{k k}

pontja, amelyre fennáll az

\begin{matrix} \vec{O T_{k}} + \vec{O T_{k}^{*}} = {\vec{O T}}_{k k} \end{matrix}

reláció. Másrészt

t_{k k}

-nak

N_{k}

-val ellentett oldalán az

A_{k}

-nak nincs pontja. Ezek szerint

t_{k k}

A_{k}

tartománynak, következésképpen a

C

összegtartománynak támaszegyenese.
A

C

tartomány

t_{11}

t_{22}

t_{33}

t_{44}

támaszegyenesei nyilván egy

S

támasznégyzetet alkotnak, melynek oldala, amint az az ábrából világosan kitűnik:

\begin{matrix} s = m + n . \end{matrix}

(4)

Mindezekből már világos, hogy a

C

tartomány összes támasztéglalapjai négyzetek, vagyis

C

valóban egy négyzetekkel burkolt tartomány.
Ennek a tételnek az alkalmazására nyomban mutatunk egy példát. A 3. ábra ‐ mondjuk ‐

R

szélességű REULEAUX-poligonja töltse be a

B

tag szerepét, az

A

szerepét pedig egy

r

sugarú, vagyis

2 r

szélességű körtartomány. Most az

A + B = C

összegtartomány ‐ minthogy

m = R

állandó és

n = 2 r

állandó ‐ egy

s = R + 2 r

állandó szélességű tartomány. Ez az összegtartomány a 4. ábrán látható. ^{$^{*}$}

5. Nem egybevágó négyzetekkel burkolt alakzatok

Egy ilyen példa már szerepelt: a négyzet. Nyomban fölmerül a kérdés, van-e másfajta négyszög, mely négyzetekkel burkolható ? Ezzel a kérdéssel kapcsolatban pedig az a még általánosabb kérdés is kínálkozik, hogy vannak-e négyzetekkel burkolt konvex poligonok, s ha vannak, milyen speciális formák esetében következik be a négyzetekkel való beburkolhatóság ?
Azonnal látni fogjuk, hogy nem könnyű kérdések ezek, nem is törekszünk teljességre, csupán néhány speciális esetre szorítkozunk, amelyeknek ismeretében (a II. tétel segítségével) további, újabb alakzatokat származtathatunk, melyek négyzetekkel beburkolhatók.

III. TÉTEL. Hegyesszöggel rendelkező konvex poligon nem burkolható be négyzetekkel.
BIZONYÍTÁS. Állításunk bizonyítására elegendő azt megmutatnunk, hogy bármely a mondott tulajdonságokkal bíró

P

poligonnak van olyan támasztéglalapja, amelynek szomszédos oldalai különbözők. Ha egy konvex

P

poligonnak

A_{1}

csúcsa hegyesszögű, akkor azok között a támasztéglalapok között találunk egy ilyent, amelyeknek egyik csúcsa

A_{1}

(a 11. ábrán ezt a hegyesszöget

ω

jelz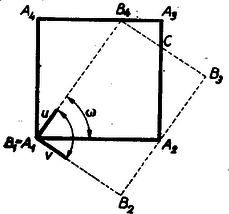i).

11. ábra

A tételt annak az állításnak az igazolásával bizonyítjuk, hogy van

P

-nek egy

A_{1}

csúcspontú támasztéglalapja.
Ha a

P

poligon

ω

szögének egyik szárához illesztett támasztéglalap, az

A_{1} A_{2} A_{3} A_{4}

alakzat nem volna négyzet, akkor már nincs mit igazolni. Tegyük hát fel, hogy ez az alakzat négyzet.
Az

ω

szög másik szára, az

u

félegyenes, metszi az

A_{3} A_{4}

szakaszt, mert különben

ω < 45^{\circ}

lenne, ami azt jelentené, hogy a támasznégyzet

A_{3} A_{4}

oldalán nincs pontja a

P

poligonnak, ez pedig a támasznégyzet fogalmából kifolyólag abszurdum. Tegyük hát fel, hogy

u

egy

B_{4}

pontban metszi a szakaszt (esetleg

B_{4} \equiv A_{3})

.
Tekintsük

P

ama támasztéglalapját, melynek

A_{1}

-nél levő derékszöge az

(u v) ∢

. Világos, hogy ez a támasztéglalap az

u

mentén nem lehet a

B_{1} B_{4}

-nél rövidebb, és a

v

mentén nem lehet a

B_{1} B_{2}

-nél hosszabb; ámde az

A_{1} B_{4}

átfogójú

A_{1} A_{4} B_{4}

és az

A_{1} A_{2}

átfogójú

A_{1} B_{2} A_{2}

derékszögű háromszögekből nyilván

A_{1} B_{4} > A_{1} B_{2}

; következésképpen a

P

tartomány

(u v)

derékszöggel meghatározott támasztéglalapja nem lehet négyzet. Tehát a

P

poligon nem burkolható be négyzetekkel.
A III. tételből azonnal következik, hogy nincs négyzetekkel beburkolható háromszög; a háromszög ugyanis legalább két csúcsában hegyesszögű. Az is nyomban következik, hagy ha egy négyszögnek nem mindegyik szöge derékszög, akkor négyzetekkel nem burkolható be; a

360^{\circ}

-os szögösszegből kifolyólag ugyanis, a mondott esetben a négyszög legalább az egyik csúcsában hegyesszögű. Sőt még a téglalap is elégtelen ahhoz, hogy négyzetekkel legyen beburkolható, hiszen a téglalap legkisebb támasztéglalapja önmaga, így nem burkolható négyzetekkel, ha az oldalai különbözők. Eszerint négyzetekkel burkolt négyszög nincs más, mint a négyzet.
Befejezésül a 12. ábrán bemutatunk egy négyzetekkel burkolt görbe határvonalú konvex alakzatot is.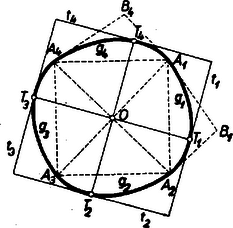

12. ábra

G

korlátos konvex tartományt a

g

zárt konvex görbe határolja. A görbe

A_{1}

A_{2}

A_{3}

A_{4}

csúcsai négyzetet alkotnak és

g_{1}

g_{2}

g_{3}

g_{4}

egybevágó ívekre bontják a görbét. Egy-egy ilyen ív bármely pontjában egy érintője van az ívnek. Ha az ív két végpontjában vett érintők, pl. az

A_{1} B_{1}

és

A_{2} B_{1}

egyenesek a mondott végpontokat összekötő (itt pl.

A_{1} A_{2}

) húrral nem-egyenlőszárú háromszöget, egymással pedig tompaszöget (itt pl.

A_{1} B_{1} A_{2} ∢

-et) zárnak be, akkor biztos, hogy

G

négyzetekkel burkolt, de nem állandó szélességű alakzat.
A leírásból ugyanis világos, hogy

G

-t középpontja, az

O

pont körül derékszöggel elforgatva, újból a

G

alakzat adódik. Így a derékszögű elforgatással önmagába átmenő ama négyszög, melynek oldalegyenesei a

t_{1}

t_{2}

t_{3}

és

t_{4}

egyenesek, nem más, mint négyzet. Ezek a támasznégyzetek pedig nem mind egybevágók. Az

A_{1}

pontban ugyanis az

A_{1} B_{4}

és

A_{1} B_{1}

érintők ‐ az ilyen érintőkre fentebb mondott kirovások következtében ‐ úgy állnak, hogy

\begin{matrix} A_{4} A_{1} B_{4} ∢ + A_{2} A_{1} B_{1} ∢ = A_{1} A_{2} B_{1} ∢ + A_{2} A_{1} B_{1} ∢ < 90^{\circ} \end{matrix}

és

\begin{matrix} A_{4} A_{1} B_{4} ∢ \neq A_{2} A_{1} B_{1} ∢ . \end{matrix}

Világos, hogy az

A_{1} B_{4}

és

A_{1} B_{1}

egyenes

O

-tól való távolsága más-más. Ennélfogva az a két támasznégyzet, melynek

A_{1} B_{4}

, illetve

A_{1} B_{1}

az egyik oldalegyenese, más-más nagyságú. (Ezek a négyzetek az ábrán nem szerepelnek.)

^{$^{*}$}Az 1. közlemény 3. lap 7‐9 sora így helyesbítendő: ,,melyeket négyzet keretben forgatva az alakzatok kerületét a keret oldalai hézagtalanul körülsúrolják''.

^{$^{*}$}Itt csak az alakját és az állását tekintettük az összegtartománynak; ne feledje azonban az olvasó, hogy összegtartomány képezésének előfeltétele egy $O$ kezdőpont megválasztása.