Kezdőlap


Cím:	Négyzetekkel burkolt konvex alakzatok (1. közlemény)
Szerző(k):	Kárteszi Ferenc
Füzet:	1959/január, 1 - 6. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek
Hivatkozás(ok):	Feladatok: 1959/március: 965. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(1. közlemény)

Mondanivalóinkat egy egyszerű észrevételből kiinduló probléma‐felvetéssel kezdjük (1. ábra). Tekintsük az adott K négyzetet, s az egymásra merőleges

x

és

y

irányokat. Szorítsuk a négyzetet az adott irányokkal párhuzamos határú két sáv határai közé; a

(t_{1} t_{2})

és

(t_{3} t_{4})

sávokról van szó. Könnyű belátni, hogy e két sáv közös része ugyancsak négyzet, egy a K köré írt négyzet.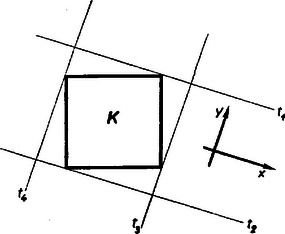

1. ábra

Ha az

(x y)

derékszöget elforgatva más‐más állásban vesszük, a megfelelő sávok kereszteződése mindig négyzetet alkot. Magát a K négyzetet is megkaphatjuk ilyen módon, ha az

x

és

y

egyenesek éppen e négyzet oldalaival párhuzamosak. A K négyzet köré írható négyzetek között maga a K négyzet a legkisebb; a legnagyobb pedig akkor adódik, ha

x

és

y

a K négyzet átlóival párhuzamosak. A K négyzet köré írt összes négyzetek a K négyzetet beburkolják.
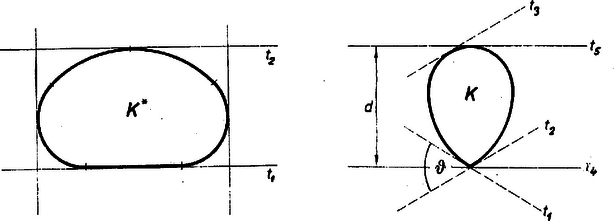
Hasonló módon szorítottuk két egymásra merőleges sáv határai közé a

2 a

ábra

K^{⋆}

alakzatát is. Itt azonban a

(t_{1} t_{2})

és

(t_{3} t_{4})

sávok közös része nem négyzet, hanem csak téglalap. A

K^{⋆}

köré írt téglalapok között akadhat speciálisan négyzet is, de az a tulajdonság, hogy az alakzatot burkoló téglalapok mind négyzetek ‐ mint az 1. ábra esetén ‐, nyilván speciális tulajdonság.
Fölmerül hát a következő kérdés. Van-e a négyzeten kívül még más olyan alakzat is, melynek az összes köré írt téglalapjai négyzetek? Ha vannak ilyenek, miképpen állíthatók elő?

1. A konvex alakzatokról

Konvex alakzaton olyan alakzatot értünk, mely bármely két pontjával együtt a két pontot összekötő szakaszt is tartalmazza. Ilyen alakzatra példa a négyzetlemez, a körlemez, a párhuzamos egyenesek határolta sáv, az egyenes határolta félsík, a

180^{\circ}

-nál kisebb szög szárai határolta szögtartomány. Az első kettő olyan alakzat, melyhez található az alakzat összes pontjait belső pontként tartalmazó fedőkör; az ilyen alakzatot korlátosnak nevezzük.
Ha a konvex alakzat korlátos, akkor a határpontjai egyszerű zárt vonalat alkotnak. Egyszerű zárt vonalon azt értjük, hogyha a vonal mentén a síkot átvágjuk, a sík két részre esik szét. Így pl. a 8-as nem egyszerű zárt vonal. Az egyszerű zárt vonalnak része lehet egyenes szakasz is, példa az 1. ábrán K és a

2 a

ábrán a

K^{⋆}

határvonala.
A következőkben röviden csak konvex tartományokról beszélünk, de ezen mindig a korlátos konvex alakzat pontjainak összességét értjük; vagyis a végtelenbe terjedő konvex tartományokat ‐ ilyen pl. a hiperbola egyik ága által, vagy a parabola által határolt konvex tartomány ‐ a továbbiak során kirekesztjük.

2a. ábra 2b. ábra

Támaszegyenesen olyan egyenest értünk, mely a konvex tartomány egy vagy több határpontját tartalmazza, de nem tartalmazza egyetlen belső pontját sem. Ilyenek a

2 a

ábrán szereplő

t_{1}

t_{2}

...

egyenesek; a

K^{⋆}

-hoz tartozó

t_{1}

támaszegyenes szemlélteti a több határpontot tartalmazó esetet, a határvonal egy egyenes szakaszát tartalmazza. A konvex tartomány a támaszegyenes létesítette két félsík egyikén helyezkedik el. A támaszegyenes a határvonalnak nem föltétlenül érintője, példa rá a

2 b

ábra K tartománya csúcsán átmenő bármely olyan egyenes, mely a

ϑ

szöget kettévágja. Minden határponton legalább egy támaszegyenes megy át.
Két párhuzamos támaszegyenes a tartomány egy támaszsávját határolja, ilyen a K-hoz tartozó

(t_{4} t_{5})

2 b

ábrán;

d

a tartomány szélessége a

(t_{4} t_{5})

sávra merőleges irányban. Két egymásra merőleges támaszsáv ‐ ilyen a

K^{⋆}

-hoz tartozó

(t_{1} t_{2})

és

(t_{3} t_{4})

‐ közös része támasztéglalap, speciálisan támasznégyzet is lehet.
Az új elnevezések birtokában feladatunkat a következő módon fogalmazhatjuk. Van-e olyan konvex tartomány, melynek összes támasztéglalapjai négyzetek; nevezzük az ilyent négyzetekkel burkolható tartománynak.

2. Egybevágó négyzetekkel burkolható konvex alakzatok

Először feladatunk egy önmagában is érdekes speciális esetével foglalkozunk, azzal az esettel, midőn az alakzatot beburkoló négyzetektől még azt is megköveteljük, hogy legyenek egymással egybevágók. Tudjuk, hogy a kör ilyen tulajdonságú alakzat, sőt 1778-ig azt hitték a matematikusok, hogy más ilyen tulajdonságú alakzat nincs is. Euler (1707‐1783) fedezte fel, hogy előállítható más alakzat is, mely egymással egybevágó négyzetekkel burkolható be, s az ilyeneket a körhöz hasonló tulajdonságukra való tekintettel orbiformoknak nevezte. A petrográdi (ma Leningrád) akadémia kiadványában, 1778-ban közölte felfedezését, mely nagy meglepetést keltett.
Azonnal belátható, hogy a négyzetekre vonatkozó kirovással való definíciót a következő egyenértékű kirovással helyettesíthetjük: legyenek az alakzat támaszsávjai egyenlő szélességűek. Ebből a definícióból érthetővé válik, hogy a későbbi kutatók miért nevezték állandó szélességűnek a szóban forgó alakzatot.
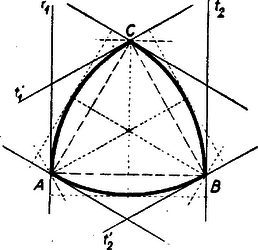
Barbier¹ fedezte fel 1860-ban azt az érdekes tulajdonságot, hogy a

d

állandó szélességű alakzatok bármelyikének a kerülete

d π

. Reuleaux² a mozgási mechanizmusokat tanulmányozván olyan alakzatokat szerkesztett, melyeket négyzet keretben forgatva az alakzatok kerületét a keret oldalai hézagtalanul végigsúrolják. (Ilyen pl. a 3. ábrán bemutatott ún. Reuleaux-féle háromcsúcsos körívpoligon.)
A magyar matematikusok közül időrendben Jordan Károly volt az első, aki ebben a témakörben figyelemre méltó eredményeket produkált. Termékeny kutató módszert dolgozott ki a konvex görbékkel kapcsolatos problémák megoldására és szép tételekkel gazdagította a szóban forgó geometriai tárgykört. (Vizsgálatait ismertető műve 1915-ben jelent meg.)
Most az állandó szélességű alakzatokra egy Reuleaux-tól eredő példát ismertetünk (3. ábra).

3. ábra

A B C

szabályos háromszög csúcsai mint középpontok köré az oldalával egyenlő sugárral köröket írva, a három körtartomány közös részeként az

A B C

ívháromszög adódik. Könnyű belátni, hogyha

(t_{1} t_{2})

támaszsáv egyik határa az

\hat{A C}

köríven (mint érintő)

A

-tól

C

-ig gördül, akkor a másik határa a

\hat{B C}

ívet

B

-ben érintő állásból kiindulva a

B

csúcs körül forog, amíg a

\hat{B A}

ívet

B

-ben érintő állást el nem éri. Ezalatt a sáv irányváltozása

60^{\circ}

. Ha folytatjuk a sáv forgatását, akkor a forgási középpont szerepét a

C

pont veszi át, vagyis a sáv

t_{1}

határa forog a

C

körül és

t_{2}

gördül a

\hat{B A}

íven. Az előbb jellemzett

60^{\circ}

-os irányváltozás a sáv teljes forgása során 6 fázisban lép fel, a határegyenesek forgása és gördülése váltakozik. A teljes körülforgatás során a sáv szélessége állandóan ugyanakkora marad.
Ha

A B = d

, akkor az

A C B ∢ = π / 3

következtében

\hat{A B} = d π / 3

, tehát az

A B C

ívháromszög kerülete

d π

, ami Barbier általános tétele szerint előre tudható volt.
A Reuleaux‐poligonokból könnyen származtathatunk törés nélküli görbét, mely szintén állandó szélességű (4. ábra).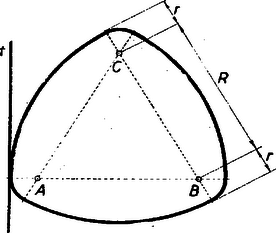

4. ábra

Írjunk ugyanis a Reuleaux-háromszögek

60^{\circ}

-os

R

sugarú ívei helyett velük koncentrikus, ugyancsak

60^{\circ}

-os, de

R + r

sugarú köríveket. Az ívek közötti hézagok az

A

B

C

középpontok köré írt

r

sugarú

60^{\circ}

-os körívekkel megszüntethetők. Az így szerkesztett görbe sehol sem törik meg, mert a kétféle körív csatlakozási pontjában az ívek érintői egybeesnek; az

A B C

háromszög ama oldalára ugyanis, mely a mondott csatlakozási ponton megy át, mindkét ív érintője merőleges. Könnyű belátni, hogy e görbe bármely két egymással párhuzamos érintője érintési pontjait összekötő egyenes szakasz az

A

B

C

, pontok egyikén (esetleg kettőn is) átmegy és

r + (R + r) = d

a szakasz hosszúsága. Tehát e görbével határolt bármilyen irányú támaszsáv szélessége

R + 2 r = d

.
A teljes görbe most három, egyenként

(R + r) π / 3

hosszúságú és három, egyenként

r π / 3

hosszúságú körívből tevődik össze. Következésképpen a tartomány kerülete

d π

3. Az összegtartomány fogalma

H. Minkowszki az 1897‐1911 közötti időszakban nagy jelentőségű eredményeket ért el a konvex alakzatokra vonatkozó kutatásai során. Ő vezette be az összegtartomány fogalmát is, ami igen hasznosnak bizonyult. Mi is hasznosítani fogjuk olyan módon, hogy néhány ismert, négyzetekkel burkolt konvex tartományból újabb, még nem ismert, ugyancsak négyzetekkel burkolt tartományokat származtatunk le éppen a tartományok összeadása segítségével. Az összegtartomány fogalmát most többféleképpen megvilágítva vezetjük be.
Állapodjunk meg a tartományok közötti egyenlőség következő értelmezésében: Tekintsük egyenlőnek az

A

és

A'

tartományokat, ha van olyan eltolás, mely az

A

tartományt az

A'

tartományba átviszi. (Az el nem mozdítást is eltolásnak tekintjük.) A fizikából tudjuk, hogy két eltolás együttes hatása egyetlen eltolással is elérhető. Így világos, hogy a tartományok most értelmezett egyenlősége rendelkezik a következő tulajdonságokkal (amelyek a számok közti egyenlőségre jellemzőek):

A = A'

.
2. Ha

A = A'

, akkor

A' = A

.
3. Ha

A = A'

és

A' = A''

, akkor

A = A''

.
Legyen az A tartomány és az

Y

pont

A + Y = C

összegének egy adott

O

kezdőpontra vonatkoztatott értelmezése a következő. Az

\begin{matrix} \vec{O X} + \vec{O Y} = \vec{O Z} \end{matrix}

(1)

vektor összefüggés egy

Z

pontot definiál. Ha

X

az A tartomány összes pontjait leírja (5. ábra), akkor

Z

leír egy C tartományt.

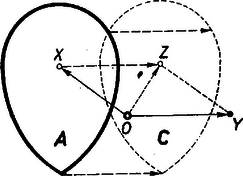5. ábra

Az ábra segítségével azonnal belátható, hogy ha A-t az

\vec{O Y}

vektornak megfelelő eltolással elmozgatjuk, a C tartományt kapjuk.
Ha most az

Y

pont szerepét egy B tartomány veszi át, vagyis ha úgy származtatjuk a

Z

pontokat, hogy

X

az A és

Y

a B tartomány összes pontjait leírja (6. ábra), akkor

Z

leír egy C tartományt. Ez az

\begin{matrix} A + B = C \end{matrix}

összegtartomány, mégpedig az

O

kezdőpontra vonatkozólag.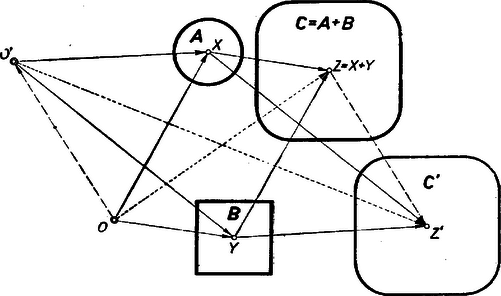

6. ábra

Az ábrából azonnal kiolvasható, hogyha C bármely

Z

pontjáról van szó, az

O

kezdőpontnak egy

O'

-vel való helyettesítése

Z

helyett egy olyan

Z'

-t szolgáltat, melyre nézve

\begin{matrix} \vec{Z Z'} = - \vec{O O'} . \end{matrix}

(2)

Eszerint

C'

eltolással adódik

C

-ből. Az eltolás a

- \vec{O O'}

vektornak felel meg. Az egyenlőség értelmezése szerint pedig

C = C'

, tehát az összeg ebben az értelemben független a kezdőponttól. Ezt a körülményt fejezi ki az a fogalmazási mód is, hogyha A és B adott, akkor a

C = A + B

összegtartomány eltolás erejéig egyértelműen határozott.
Az sem változtatja meg az összegtartományt, ha az összeadandó tartományok bármelyikét előbb eltoljuk, s azután képezzük az összeget. Részletesebben, ha az

A + B = C

összegtartomány ‐ mondjuk ‐

B

tagját egy eltolás átviszi

B'

-be, és

A + B' = C'

, akkor ugyanaz az eltolás

C

-t átviszi

C'

-be. Elegendő evégből az A tartomány tetszőleges

X

és a B tartomány tetszőleges

Y

pontjára belátni, hogy az

Y

pontot egy

Y'

-be átvivő eltolás a

Z

összegpontot a

Z'

összegpontba viszi át, ahol az

\begin{matrix} \vec{O X} + \vec{O Y} = \vec{O Z}, \vec{O X} + \vec{O Y'} = \vec{O Z'} \end{matrix}

(3)

relációk definiálják a

Z

és

Z'

pontokat. Ennek az állításnak a helyessége pedig a 7. ábrából már könnyen belátható.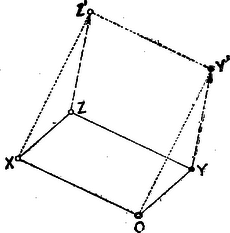

7. ábra

Azt kell ugyanis belátni az összegpontokat szolgáltató

O X Z Y

és

O X Z' Y'

vektor‐paralelogrammák közvetitésével, hogy

\vec{Y Y'} = \vec{Z Z'}

. Minthogy

\vec{O X} = \vec{Y Z} = \vec{Y' Z'}

, az egymással párhuzamos és egyenlő

Y Z

Y' Z'

szakaszok végpontjai egy újabb paralelogramma csúcsait szolgáltatják. Eszerint valóban

\vec{Y Y'} = \vec{Z Z'}

.
Adva vannak az A és B tartományok, az

A + B = C

összegtartományt most lefedéssel értelmezzük (8. ábra).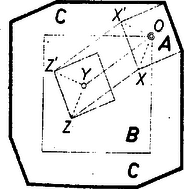

8. ábra

Az A tartományból kiválasztunk egy tetszőleges pontot és azt vesszük kezdőpontnak. Az ábrán A egy négyzet, annak a középpontját választottuk kezdőpont gyanánt. Toljuk el a B tartományt úgy, hegy a kerületén helyezkedjék el az

O

pont. Az ábrán a B négyzet jobb felső sarkát egyesítettük

O

-val. (Ezzel az előkészítéssel csak azt igyekeztünk biztosítani, hagy az ábra ne húzódjék szét. Az előkészítés olyan változtatásokból áll, melyekről már tudjuk, hogy az összeget nem változtatják meg, hiszen az összegtartomány eltolását nem tekintjük lényeges változásnak.)
Szerkesszük meg rendre az (1) relációnak megfelelő pontokat, mégpedig a következő lépések során. A B tartomány egy

Y

pontját rögzítjük, az A tartományt pedig leírjuk egy

X

ponttal. Ezalatt a

Z

pontok a teljes C tartomány egy részét írják le, egy az A-val egyező állású, egybevágó idomot. Ha most az

Y

is változik, s leírja a B tartományt, akkor más‐más

Y

-hoz az összegnek más‐más részét kapjuk. Az így kapott tartományrészek lefedte pontok összessége alkotja C-t.
Ezt a fokozatos összeg‐előállítást szemléletesebben is elmondhatjuk. Készítsük el az A négyzetet a rajta feltüntetett

O

középponttal együtt végtelen sok példányban. Helyezzük az összes példányokat a B tartományra úgy, hogy a B minden egyes pontjára egy‐egy példány

O

pontja helyezkedjék, és minden példány állása a 8. ábra A tartományának állásával egyezzék meg. A szóban forgó végtelen sok négyzetlemez lefedi a sík egy részét. A lefedett síkrész éppen a C összegtartomány. A példa esetében a vastag vonallal határolt nyolcszögtartomány.

¹Olv.: bárbjé.

²Olv.: rőló.