Cím: Az 1958. évi Arany Dániel matematikai tanulóverseny: a II. fordulón kitűzött feladatok megoldása
Füzet: 1958/november, 71 - 79. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye:

 

1. feladat: a-nak mely értékeinél lesz a 97a2+84a-55 kifejezés számértéke a-nak többszöröse?
 

Megoldás: Azt mondjuk, hogy egy c egész szám többszöröse egy d egész számnak (vagy, hogy c osztható d-vel, vagy d osztója c-nek), ha van olyan q egész szám, amelyre c=dq. Oszthatósági kérdésekben célszerű lehet pozitív osztókra szorítkozni, vagyis d-ről, vagy esetleg a definícióban szereplő mindegyik számról feltenni, hogy természetes szám, máskor viszont éppen fordítva, célszerű minden egész számot megengedni.
Azt a kérdést kell tehát megvizsgálni, hogy milyen a egész számokhoz, illetőleg pozitív egész számokhoz van olyan k egész szám, amelyre teljesül a
97a2+84a-55=ka(1)
egyenlőség. Az a-t tartalmazó tagokat egy oldalra rendezve és a-t kiemelve
(97a+84-k)a=55.

Ezek szerint 55-öt kell két pozitív egész, ill. két egész tényező szorzatává alakítani. Pozitív egész tényezős felbontások 1⋅55, 5⋅11, továbbá a tényezők felcserélésével keletkező felbontások, a további egész felbontások pedig úgy keletkeznek, hogy a pozitív felbontások mindkét tényezőjének negatívját vesszük. Így a következő pozitív egész a értékek felelnek meg: 1, 5, 11, 55, az összes egész értékeket tekintve pedig ezekhez negatívjaik: -1, -5, -11, -55 járulnak.
 

Megjegyzés: Bollobás Béla felvetette azt az általánosabb kérdést is, hogy a-ról nem tételezve fel, hogy egész, milyen a értékekre lesz a szóban forgó kifejezés a-nak egész számszorosa, vagyis milyen (nem feltétlenül egész) a számokra áll fenn (1) egész k-val. A feladat fogalmazása ezt az értelmezést is megengedi, ez a kérdés azonban már nem tárgyalható a fenti módon. A kérdés most az, hogy milyen a-kra teljesül egész k-val a
97a2+(84-k)a-55=0(2)
egyenlet. Itt k akkor és csak akkor egész, ha a 84-k=l szám egész. Ezt a jelölést bevezetve az
a=-l±l2+21340194,(l=0,±1,±2,...)
számok és csak ezek felelnek meg a felvetett követelményeknek.
 

2. feladat. Pótoljuk a hiányzó számjegyeket az alábbi osztásban:
xxxxxx:xxx=xx8-xxx5xxxx-9xxxxxxxx

 

Megoldás: Az utolsó részletszorzatból látható, hogy az osztónak, amely 3 jegyű, 8-szorosa is háromjegyű, tehát az osztó kisebb, mint 1000/8=125.
Az első részletszorzat négyjegyű és utolsó jegye 5. Utóbbiból következik, hogy az osztó utolsó jegye 5, előbbiből pedig az, hogy a hányados első jegye 9 (mivel az osztó 8-szorosa még 3 jegyű) és az osztó legalább 1000/9=11119.
A három megállapításból együtt következik, hogy az osztó csak 115 lehet.
A második részletszorzat 3 jegyű és első jegye 9, így a hányados második jegye 8, mert az osztó 9-szerese 4 jegyű, 7-szerese pedig 900-nál kisebb.
Az osztó és a hányados ismeretében a még ismeretlen jegyek már megállapíthatók:
113620 :  115 =  98810351012920920920

 

3. feladat. Fusson végig a P pont az ABCD négyzet kerületén. Legyen Q a síknak egy olyan rögzített pontja, amely nincs rajta a négyzet egyik oldalán sem. Legyen PQR egyenlő oldalú háromszög. Mi az R pontok mértani helye?
 

Megoldás: A PQ szakasz fölé két szabályos háromszög írható, amelyeknek PQ közös oldala. Ha egy szabályos háromszög egy csúcsa körül az egyik oldalát megfelelő irányban 60∘-kal elfordítjuk, akkor ez a csúcsból induló másik oldalt fedi. Ha az utóbbi oldalt akarjuk az előbbivel fedésbe hozni, ezt az első forgatással ellentétes irányú 60∘-os elforgatással érhetjük el.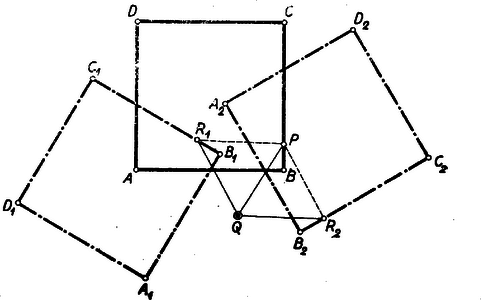
 

 

Legyen a PQ szakasz fölé rajzolható két szabályos háromszög PQR1 és PQR2 a betűzést úgy választva, hogy QP-t QR1-be pozitív (az óramutató járásával ellentétes), QR2-be pedig negatív irányban lehessen 60∘-os elforgatással beleforgatni.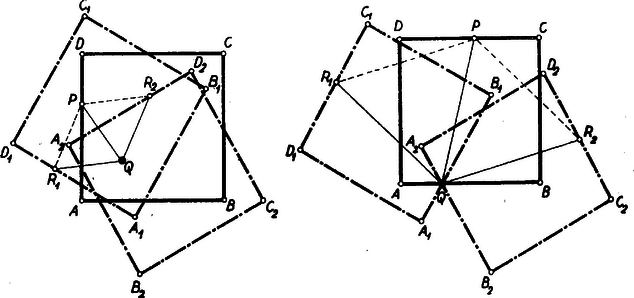
 

 

Ekkor az R1 pontok is, az R2 pontok is egy-egy ABCD-vel egybevágó négyzetet, A1B1C1D1-et, ill. A2B2C2D2-t fogják befutni egyszer, míg P végigfut az ABCD négyzeten. Ez a két négyzet úgy keletkezik az adottból, hogy ezt Q körül 60∘-kal elforgatjuk pozitív, illetőleg negatív irányban.
Valóban, az ABCD négyzet bármely P pontját Q körül 60∘-kal elforgatva pozitív irányban egyrészt az A1B1C1D1 négyzet egy R1 pontját kapjuk, másrészt viszont R1 az elmondottak szerint a PQ-ra rajzolható szabályos háromszög egyik csúcsa. Fordítva, ha az A1B1C1D1 négyzet egy R1 pontját forgatjuk el Q körül negatív irányban 60∘-kal, akkor egyrészt az ABCD négyzet egy P pontjába jutunk vissza, másrészt PQR1 olyan szabályos háromszög, amelyben a QP oldal Q körül pozitív irányú 60∘-os elforgatással hozható QR1-gyel fedésbe. Ugyanez áll pozitív és negatív forgatás felcserélésével az A2B2C2D2 négyzetre vonatkozóan is. Ezzel állításunkat igazoltuk.
 

Megjegyzések: 1. Az ABCD négyzet semmilyen tulajdonsága nem szerepelt meggondolásainkban, így bármilyen síkidom pontjain is futtatjuk végig P-t, a feladatban leírt eljárással a síkidomnak Q körül pozitív és negatív irányban 60‐60∘-kal elforgatott képét kapjuk mértani helyül.
 

2. Meggondolásaink abban az esetben is érvényesek, ha Q a négyzet (illetőleg az adott síkidom) egy pontja, kivéve ha P egybeesik Q-val, amikor szabályos háromszög nem alkotható. Ez esetben célszerű ,,elfajult szabályos háromszög"-nek tekinteni egy pontot (mely a háromszög három egybeeső csúcsa).
 

Haladók (II. osztályosok) versenye.
 

1. feladat. Egy hatjegyű négyzetszámot kétjegyű részekre vágva megállapítjuk, hogy az utolsó kétjegyű szám megegyezik a középső kétjegyű számmal, míg az első kétjegyű szám a középső kétjegyű számot 100-ra egészíti ki. Melyik ez a négyzetszám?
 

I. megoldás: A keresett négyzetszámot n2-tel jelölve feltehetjük, hogy n pozitív egész, mert egy számnak és a negatívjának ugyanaz a négyzete. Mivel n2 hatjegyű, így
317≦n≦999.

Az n2 utolsó két jegyéből alakított számot a-val jelölve, a feladat feltételei szerint
n2=10000(100-a)+100a+a=1000000-9899a.

Itt 9899 törzstényezős felbontása 19⋅521 s így az utolsó tagot fejezve ki a nyert egyenletből
19⋅521a=1000000-n2=(1000+n)(1000-n).(1)

Tudjuk, hogy egy szorzat csak úgy lehet osztható egy törzsszámmal, ha már valamelyik tényező is osztható a törzsszámmal. Ezt az 521-re alkalmazva az első tényezőre
1317≦1000+n≦1999,
s így csak akkor lehet 521-gyel osztható, ha 3⋅521=1563-mal egyenlő; a második tényező pedig csak úgy, ha 521-gyel egyenlő. Az első esetben
n=563n2=316969(2)
kielégíti a feladat feltételeit, a második esetben a=479, 1000+n=1479=3⋅17⋅29 nem osztható 19-cel, s így (1) nem teljesülhet. A feladatnak tehát egy megoldása van, a (2) alatti.
 

Megjegyzés: Néhányan a négyzetszám első két jegyéből álló b számból indultak ki. Az erre nyerhető n2=9899b+10100 egyenletből legfeljebb akkor sikerül további következtetéseket levonni, ha észreveszi valaki, hogy 10100 egy négyzetszám és egy 521-gyel osztható szám összegére bontható:
10100=16⋅521+422
s így
(n+42)(n-42)=521(19b+16).

Ez az észrevétel azt mutatja, hogy néha még a jelölések szerencsés megválasztása is lényeges lehet egy feladat megoldásában.
Többen abból indultak ki, hogy mik fordulhatnak elő négyzetszám utolsó két jegyeként, de szintén nem jutottak eredményre. Kétségtelenül hosszadalmasabb ez az út a fenti megoldásnál, de járható, mint a következő megoldás mutatja:
 

II. megoldás: Egy szám négyzetének utolsó két jegye csak a szám utolsó két jegyétől függ, más szóval, ha két szám 100-zal osztható számban különbözik, akkor a négyzetük is, mert
(100a+b)2=10000a2+200ab+b2=100(100a+2ab)+b2.
Elég tehát a 0-tól 100-ig terjedő számok utolsó két jegyét vizsgálni. De már a 0-tól 50-ig tartó számok végződése is kiad minden végződést, 50-en fölül csak ismétlődnek sorra ugyanazok a végződések, mert
(50+a)2=2500+100a+a2=100(25+a)+a2,
sőt már 50-ig is párosan fordulnak elő a végződések: a 25-re szimmetrikusan elhelyezkedő számok négyzetének utolsó két jegye megegyezik. Valóban egy x számmal a 25-re nézve szimmetrikusan az 50-x szám helyezkedik el és
(50-a)2=2500-100a+a2=100(25-a)+a2.

A négyzetszámok lehetséges végződéseit (utolsó két jegyét) tehát megkapjuk, ha 0-tól 25-ig nézzük meg a számok négyzetének utolsó két jegyét. Így a következő végződések adódnak:
00010409162124252936414449566164697681848996.
Ezek mindegyikéhez elkészíthetjük a feladatban leírt számot és négyzetgyök-vonással eldönthetjük, hogy az négyzetszám-e vagy sem. Valamivel azonban még megkönnyíthetjük a számolást: Egy páros szám négyzetének 2 páros hatványával, egy 3-mal osztható szám négyzetének 3 páros hatványával kell oszthatónak lennie. Ismeretes, hogy minden páratlan szám négyzete 8k+1 alakú. Könnyen belátható, hogy 3-mal nem osztható szám négyzete mindig 3k+1 alakú, tehát négyzetszám 3k+2 alakú nem lehet és hasonló megszorításokat megállapíthatunk más prímszámokkal kapcsolatban is.
A felsorolt végződések elsője és utolsója elesik, mert azokhoz képezve a feladat kikötéseit teljesítő számot nem 6-jegyű számhoz jutunk. A 01-hez, 09-hez, 25-höz, 41-hez, 49-hez, 81-hez és 89-hez tartozó számok 8-cal osztva 5-öt adnak maradékul és így nem lehetnek négyzetszámok, a 24-hez és 56-hoz tartozó pedig azért nem, mert 8-cal osztható, de 16-tal nem. A 3-mal, illetőleg 9-cel való oszthatóságot nézve a 04-hez, a 16-hoz, 61-hez és a 76-hoz tartozó számok 3-mal osztva 2-t adnak maradékul, a 29-hez és a 64-hez tartozó szám pedig osztható 3-mal, de 9-cel nem, tehát ezek sem négyzetszámok. A maradó számok közül a 21-hez tartozó osztható 11-gyel, de 121-gyel nem, a 36-hoz tartozó pedig osztható 7-tel, de 49-cel nem. A maradó három számból (a 44-hez, 69-hez és 84-hez tartozóból) négyzetgyököt vonva ezúton is azt találjuk, hogy a 316969 szám az egyetlen, amelyik megfelel a feladat feltételeinek.
 

2. feladat. Egy turista csoport A-ból B-be autóbuszon akar eljutni, azonban csak egy olyan autóbusz áll rendelkezésére, amely egyszerre a társaságnak csak egynegyed részét képes felvenni, és nincs elég idő arra, hogy egymás után szállítsa el őket A-tól B-ig.
Ezért a társaság egyszerre indul el, mégpedig egynegyed része autóbuszon, a többi gyalog. Az autóbusz az első csoportot valahol az út közbeeső pontján teszi le, majd visszafordul, felveszi a társaság második negyedét, de őket sem szállítja végig, hanem visszatér a harmadik csoportért, majd hasonló módon a negyedikért, amelyet végül B-ig szállít. A szállítást úgy bonyolítják le, hogy mind a négy csoport egyidejűleg érkezik B-be.
Feltéve, hogy mind az autóbusz, mind a gyalogosok sebessége állandó és az autóbusz sebessége a gyalogosok sebességének 7-szerese, a turisták útjuk hányadrészét teszik meg autóbuszon, ill. gyalog? Hányszor annyi időre lett volna szükség az út megtételéhez abban az esetben, ha az autóbusz mind a négy csoportot A-tól B-ig szállítja?
 

Megoldás: Mind a négy csoport egyszerre indul és egyszerre érkezik meg. Ez csak úgy lehet, ha mind a négy csoport ugyanakkora utat tesz meg autóbuszon és mind a négy csoport egyenlő hosszú szakaszon gyalogol.
Jelöljük egy csoport autóbuszon megtett útját l-lel. Ekkora gyalogló turisták l/7 hosszúságú utat tesznek meg, amíg az autóbusz az első csoportot leteszi, majd a gyalogosokkal való találkozásig a köztük levő 6l/7 hosszú útból 7-szer annyit tesz meg a busz, mint a gyalogosok, vagyis ennek az útszakasznak hét nyolcad részét, 3l/4 távolságot. A második csoport így l/4 utat tesz meg az autóbuszra szállásig, a harmadikra további l/4, a negyedikre pedig összesen 3l/4 út megtétele után kerül sor, a csoportok tehát 3l/4 utat tesznek meg gyalog és l utat autóbuszon, vagyis az egész út három hetedén gyalogolnak és négy hetedét teszik meg autóbuszon.
Az autóbusz a B-be érkezésig négyszer tett meg l hosszúságú utat B felé és háromszor 3l/4 hosszúságú utat A felé, tehát összesen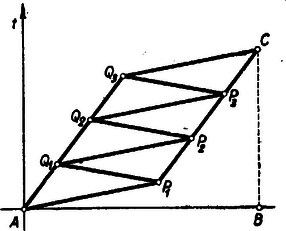
4l+9l4=254l
hosszúságú utat tett meg, míg ha mindenkit A-tól B-ig szállít, akkor négyszer B felé és háromszor vissza A-ba a teljes 7l/4 hosszúságú utat, tehát összesen 49l/4 hosszúságú utat kell megtennie. Ehhez 49/25-ször, tehát majdnem kétszer annyi időre lenne szükség.
 

 

A túráról grafikont készítve ‐ a vízszintes tengelyen az utat, a függőlegesen az időt tüntetve fel ‐ az egymás utáni csoportok mozgását az AP1C, AQ1P2C, AQ2P3C, AQ3C vonalak ábrázolják, az autóbuszét pedig AP1Q1P2Q2P3Q3C.
 

3. feladat. Adott az A1B1C1 hegyesszögű háromszög. Szerkesztendő az ABC háromszög azzal a feltétellel, hogy az A1 pont a BC oldal fölé kifelé rajzolt szabályos háromszög csúcspontja, hasonlóképpen a B1 és C1 pont a CA és AB oldal fölé kifelé rajzolt szabályos háromszög csúcspontja.
 

I. megoldás: Szerkesszük meg először valamely ABC háromszöghöz az A1B1C1 háromszöget (1. ábra), majd az így nyert ábrát próbáljuk meg úgy kiegészíteni,hogy a szerkesztést visszafelé is elvégezhessük.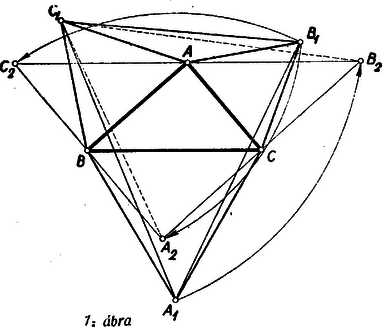
 
 

A szabályos háromszögek mindegyik szöge 60∘-os, ezért célszerűnek látszik 60∘-os elforgatásokat alkalmazni. Forgassuk pl. az ábra C1BA1 háromszögét a C1 pont körül befelé (pozitív értelemben), ekkor a 60∘-os elforgatással a B pont az A pontba kerül, az A1 pont elforgatott helyzetét jelöljük B2-vel. Miután BA1 szakasz 60∘-kal fordult el, párhuzamos helyzetbe került BC-vel, és tekintve, hogy egyenlő is vele, ezért a BCB2A négyszög paralelogramma. Ha most a C1AB1 háromszöget forgatjuk el ugyancsak befelé (ezúttal negatív értelemben) a C1 pont körül, a BACA2 paralelogrammát nyerjük (A2-vel B1 pont elforgatott helyzetét jelöltük). Miután a két paralelogramma közös oldala AB, egy további közös csúcsuk C, így az A2, B2 és C pontok egy egyenesbe esnek és C az A2B2 szakasz felezőpontja. A2 és B2 az adatokból megszerkeszthető, tehát ezekkel együtt C pont is, végül ugyanezzel az eljárással, amivel C-t nyertük, megszerkeszthetjük A-t és B-t. A szerkesztéssel arra jutunk, hogy a keresett ABC háromszög csúcspontjai az A1B1C1 háromszög oldalai fölé befelé rajzolt szabályos háromszögek harmadik csúcspontjai által alkotott A2B2C2 háromszög oldalainak felező pontjai.
A szerkesztés szerint a kitűzött feladat látszólag minden esetben egyértelműen megoldható. Ennek ellentmond a 2. ábrán bemutatott helyzet, amellyel az A1B1C1 háromszögből kiindulva kapunk ugyan ABC háromszöget, de A1, B1 és C1 nem az oldalakra kifelé, hanem a befelé rajzolt szabályos háromszögek harmadik csúcspontja.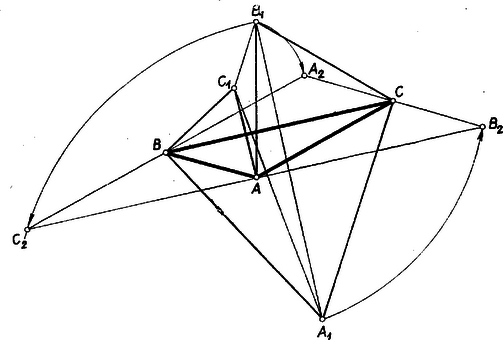
 
 
2. ábra
 

Ezen az ábrán azonban az A1B1C1 háromszög nem hegyesszögű; vegyük észre továbbá azt is, hogy az A2B2C2 háromszög körüljárási értelme ellentétes az A1B1C1 háromszögével.
Bizonyítás nélkül megjegyezzük a következőket. A feladat megoldhatóságának az a feltétele, hogy az A1B1C1 háromszög oldalai fölé befelé rajzolt szabályos háromszögek harmadik csúcsai által alkotott A2B2C2 háromszög körüljárási értelme megegyezzék az A1B1C1 háromszög körüljárási értelmével. (ABC körüljárási értelme mindig megegyezik A2B2C2 körüljárási értelmével.) Az eredeti értelmezés szerint sohasem kapunk megoldást, ha az A1B1C1 háromszögnek van 120∘-osnál nagyobb szöge, és a fennmaradó esetekben mindig kapunk megoldást, ha az A1B1C1 háromszögnek nincs 30∘-osnál kisebb szöge.
 

II. megoldás: A keresett háromszög C csúcsát pl. az jellemzi, hogy alkalmas irányban (C-től A felé) B1 körül 60∘-kal elforgatva, majd C1 körül ugyanilyen irányban 60∘-kal forgatva és végül A1 körül ugyancsak 60∘-kal elforgatva visszakerül eredeti helyzetébe.
Megmutatjuk, hogy ha ugyanezeket a forgatásokat a sík egy tetszés szerinti P pontjára alkalmazzuk, akkor a pont a kiindulási helyzetéből a második forgatás utáni helyzetbe átvihető egy alkalmas pont körüli 120∘-os forgatással, a harmadik forgatás utáni helyzetébe pedig egyetlen alkalmas 180∘-os forgatással, ahol ezek a forgatások egy-egy csak az A1, B1 és C1 pontoktól függő középpont körül történnek.
A bizonyításhoz azt fogjuk felhasználni, hogy egy K pont körül α szöggel történő elforgatás eredményét úgy is megkaphatjuk, ha húzunk a K ponton át tetszés szerint két egyenest, t1-et és t2-t úgy, hogy a t1-től a t2-ig a forgatás irányában α/2 nagyságú szög legyen és minden pontot tükrözünk először t1-re, azután t2-re. Fordítva: két ilyen tükrözés eredménye egy K körüli α nagyságú elforgatással is megkapható (3‐4. ábrák).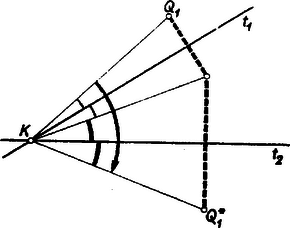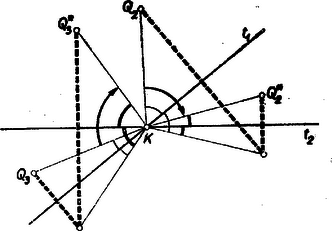
 
 
3. ábra
 
 
4. ábra
 

A B1 körüli forgatást állítsuk elő úgy két tükrözés segítségével, hogy a második tükrözés t2 tengelyéül a B1C1 egyenest választjuk, a C1 körüli forgatást pedig úgy, hogy az első tükrözés t'1 tengelyéül választjuk B1C1-et (5. 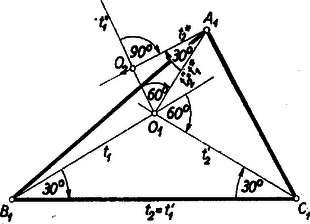ábra).
 
 
5. ábra
 

Ekkor egy tetszés szerinti pont a kétszeri forgatás után ugyanoda kerül, mintha tükrözzük a pontot t1-re, a kapott pontot t2(=B1C1)-re, az így nyert pontot t'1(=B1C1)-re, majd az újabb tükörképet t'2-re. A B1C1 egyenesre történő kétszeri tükrözés azonban visszaviszi a pontot az e tükrözések előtti helyzetébe, s így az első két forgatás eredménye ugyanaz, mintha tükrözzük a sík pontjait t1-re, majd t'2-re. Ennek a két tükrözésnek pedig ugyanaz az eredménye, mintha a két egyenes O1 metszéspontja körül végzünk (t1,t'2)=60∘ kétszeresényi, azaz 120∘-os elforgatást. Ezután még A1 körül kell 60∘-kal forgatni.
Ezeket a forgatásokat is állítsuk elő tükrözésekkel úgy, hogy két egymásutánt tükrözés tengelye O1A1 legyen. Ekkor az O1-en átmenő első tükrözési tengelyhez t''1-höz 60∘-kal kell elforgatva lennie O1A1-nek, az A1-en átmenő második tükrözés t2* tengelye pedig 30∘-kal lesz elforgatva O1A1-hez képest. A négy egymásutáni tükrözés ‐ és ezzel együtt a B1, C1, majd A1 körüli 60∘-os elforgatások ‐ végeredménye ekkor ugyanaz, mintha tükrözünk a t''1 egyenesre, azután t2*-ra. E két egyenes metszéspontját O2-vel jelölve A1O1O2 egy 30∘, 60∘, 90∘-os szögekkel rendelkező háromszög, így a három forgatás egymásutáni elvégzésével minden pont ugyanoda kerül, mintha O2 körül forgatnánk el 180∘-kal, azaz tükröznénk az O2 pontra.
Azt a C pontot kerestük, amely a tárgyalt 3 forgatás, vagy ami ugyanarra az eredményre vezet, az O2-re történő tükrözés után eredeti helyére kerül vissza, ilyen pont pedig egyedül O2. A fenti gondolatmenet szerkesztési eljárást is ad C=O2 megszerkesztésére. Az ABC háromszög további csúcsai ugyanezen a módon szerkeszthetők, vagy megszerkeszthetjük C ismeretében a BCA1 és CAB1 egyenlőoldalú háromszögeket.