Cím: Az 1958. évi Arany Dániel matematikai tanulóverseny: az I. fordulón kitűzött feladatok megoldása
Füzet: 1958/október, 40 - 46. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kezdők (I. osztályosok) versenye.

 

1. feladat.
 

Megoldás: Jelöljük az első és második kétjegyű szám tizeseit a-val, az első szám egyeseit b-vel, a második szám egyeseit c-vel.
A fenti számítási mód akkor helyes, ha a
(10a+b)(10a+c)=10a(10a+c+b)+bc
egyenlőség azonosság. Ez azonban igaz, mert mindkét oldal rendezett polinom alakja
100a2+10ab+10ac+bc.

Megjegyzések: 1. A (10a+b)(10a+c) és a 10a(10a+c+b)+bc kifejezések egyenlőségét (tetszőleges nem negatív a, b, c esetén) szemléltetni is tudjuk.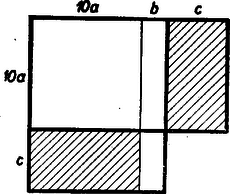
 

 

Az ábrán látható 10a+b és 10a+c oldalú téglalap területe az első kifejezést adja. A 10a és 10a+b+c oldalú téglalap területe az első téglalap területénél (a csíkozott téglalapok egybevágósága miatt) éppen egy b és c oldalú téglalap területével kevesebb.
2. A számolási eljárás változatlanul használható, ha két olyan egyenlő nagyságrendű többjegyű (esetleg tizedesjegyet is tartalmazó) számot szorzunk össze, amelynek első számjegye vagy jegyei egyenlők. Ha a két számnak ezt a közös részét jelöljük 10a-val, a maradék részeket b-vel, illetve c-vel, a bizonyítás változatlan marad. ‐ Ez a számolási mód többjegyű számoknál persze nem mindig jelent számítási könnyebbséget.
 

2. feladat.
 

I. megoldás: A betűzést az 1. ábra mutatja.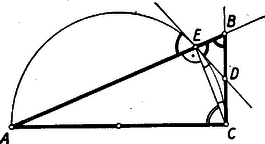
 
 
1. ábra
 

Thales tétele miatt az AEC∢ ‐ és ezért mellékszöge, a CEB∢ is ‐ derékszög. A DE és DC szakaszok egyenlőek, mert D-ből a körhöz húzott érintőszakaszok; ezért az EDC háromszög egyenlő szárú, vagyis az EC alapon fekvő két (egy ívvel jelzett) szöge egyenlő. Ebből következik, hogy az EDB háromszög két (két ívvel jelzett) szöge egyenlő, mert mindegyik az előbbi két szög egyikét 90∘-ra egészíti ki. Mivel egyenlő szögekkel szemben egyenlő oldalak vannak egy háromszögben, az EDB háromszög egyenlő szárú.
 

II. megoldás: Forgassuk el az AEC derékszögű háromszöget az E csúcs körül 90∘-kal úgy, hogy az EC oldala az EB egyenesre kerüljön (2. ábra).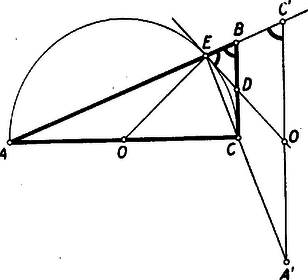
 
 
2. ábra
 

A háromszög EA oldala így EC-re kerül, a félkör O középpontjából kiinduló OE sugár pedig a rá merőleges ED érintőre. Így kapjuk az A'EC' háromszöget. Mivel BC merőleges az AC befogóra, az ennek 90∘-os elforgatásával keletkező A'C'-vel párhuzamos lesz. Az EO'C' háromszög két oldala a félkör sugarával egyenlő, s így E-nél és C'-nél levő két szöge egyenlő. De CB és A'C' párhuzamossága miatt ugyanekkora az EBD szög is. Az EBD háromszög E-nél és B-nél levő szögei tehát egyenlő nagyságúak, s így két oldala: ED és BD valóban egyenlő egymással.
 

III. megoldás: A DEB és DBE szögek egyenlőségét másképpen is beláthatjuk.
A DEB∢ csúcsszöge (az AE húr és az E-ben húzott érintő szöge) a kör AE ívén nyugvó kerületi szög (1. ábra). A DBE szöggel egyenlő ACE szög (merőleges szárú hegyesszögek) szintén az AE íven nyugvó kerületi szög. Így az ezzel a két szöggel egyenlő DEB és DBE szögek is egyenlők egymással.
 

3. feladat.
 

I. megoldás: Jelöljük OB-nek, ill. OC-nek az AD-vel való metszéspontját B1-gyel, ill. C1-gyel (1. ábra).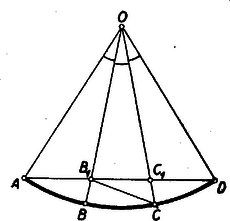
 
 
1. ábra
 

A körívet harmadoló pontokhoz húzott sugarak az O-nál levő középponti szöget is három egyenlő részre osztják. Húzzuk meg a CB1 szakaszt. Az így keletkezett OCB1 háromszög egybevágó az OAB1, háromszöggel, mert annak OB-re vonatkozó tükörképe, ugyanis az OA és OC sugarak egyenlő szöget zárnak be OB-vel.
Ha megmutatjuk, hogy a B1C1C háromszögben a C1-nél levő szög tompaszög, s így a háromszög legnagyobb szöge, ebből következni fog, hogy B1C a háromszög leghosszabb oldala; ennek következtében B1C1 kisebb B1C-nél, tehát az utóbbival egyenlő AB1-nél is. A két sugár a húrt ezek alapján nem osztja egyenlő részekre.
A B1C1C szög azonban az egyenlő szárú OB1C1 háromszög két egyenlő szöge közül az egyiknek, tehát mindenképpen egy hegyesszögnek a kiegészítő szöge, s így valóban tompaszög. Ezzel, mint láttuk, a feladatot meg is oldottuk.
Szimmetria okokból világos, hogy a C1D szakasz az AB1-gyel egyenlő.
 

II. megoldás: Jelöljük ismét B1-gyel és C1-gyel az OB és OC körsugarak metszéspontját az AD húrral (2. ábra).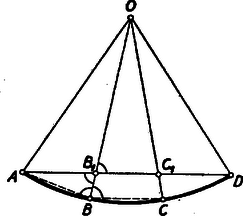
 
 
2. ábra
 

Az OB sugár az ABC szög szögfelezője, ABB1∢=B1BC∢. Az AOD szög szögfelezőjére a B1 és C1, valamint a B és C pontok tükrös helyzetűek, így B1C1 párhuzamos BC-vel, tehát B1BC∢=OB1C1∢. Az utóbbi szög csúcsszöge: AB1B szög eszerint az ABB1 szöggel egyenlő. Az ABB1 háromszög tehát egyenlő szárú, s ezért AB1=AB. Az AB mint ugyanakkora középponti szöghöz tartozó húr a BC húrral egyenlő. A BOC szög szárait metsző B1C1 és BC párhuzamos szakaszok közül a távolabbi BC a hosszabb. Így az utóbbival egyenlő AB1 szakasz hosszabb, mint B1C1.
 

Megjegyzések: 1. Azok számára, akik már ismerik egy háromszög szögfelezőjének osztásarányára vonatkozó tételt (ált. gimn. II. oszt. tananyag), közöljük a feladatnak következő egyszerű megoldását.
Az OAC1 háromszögnek az OB1 szögfelezője. A szögfelezők osztásarányára vonatkozó tétel alapján
AB1:B1C1=AO:C1O.

Mivel C1O feltétlenül kisebb, mint a kör sugara, ami AO-val egyező nagyságú, ezért AB1 és B1C1 közül a B1C1 a kisebb.
2. Ha a bizonyítottakkal ellentétben az ívet harmadoló sugarak az ívhez tartozó húrt is harmadolnák, ez lehetőséget adna egy szög harmadolására körzővel és vonalzóval, ami pedig lehetetlen (l. pl. Középisk. Mat. Lapok XIV. köt. 4. és 5. sz. 97‐107. és 129‐134. o.). ‐ Sok versenyző a szögharmadolás lehetetlenségére hivatkozva cáfolta meg a keletkező szakaszok egyenlőségét. Ez a megoldás természetesen jó, de a fenti bizonyításoknál összehasonlíthatatlanul nehezebben bizonyítható, mélyebben fekvő tételt használ fel egy ilyen egyszerű feladat megoldására.
Lukács Ottó, Scharnitzky Viktor

 

Haladók (II. osztályosok) versenye.
 

1. feladat.
 

I. megoldás: A feladat feltételei szerint a, b és c ugyan ismeretlenek, de fennállnak köztük bizonyos (ismertnek feltételezett) m és n értékkel az
a=b+cm,b=c+an
összefüggések, és meg kell határozni az a+b arányát c-hez. E célból kíséreljük meg a-t és b-t kifejezni c-vel. Az egyenleteket így írhatjuk:
ma-b=c,-a+nb=c.(1)
Innen b-t, illetőleg a-t kiküszöbölhetjük, ha az első egyenlet n-szeresét a másodikhoz adjuk, illetőleg az első egyenletet a második m-szereséhez adjuk:
(mn-1)a=(n+1)c,(mn-1)b=(m+1)c(2)
e kettő összegéből, ha mn≠1, a keresett arány
a+bc=m+n+2mn-1.

Ha mn=1, de m és n közül valamelyik nem -1, akkor a (2) egyenletekből következik, hogy c=0, s így ez esetben a kérdésnek nincs értelme.
Ha végül m=n=-1, akkor mindkét (1) alatti egyenlet az
a+b+c=0
egyenletbe megy át, és innen, ha c≠0,
a+bc=-1
adódik.
 

Megjegyzés. A feladat megoldását az tette lehetővé, hogy az a, b, c ismeretlenekre csak két elsőfokú egyenlet áll fenn, és ezekben nem fordul elő az ismeretlent nem tartalmazó tag. ‐ Az ilyen egyenleteket homogén elsőfokú egyenleteknek szokás nevezni. ‐ Egy ilyen egyenletekből álló egyenletrendszernek mindig megoldása a csupa 0-ból álló értékrendszer. Ha van ettől különböző megoldás (és esetünkben van, mert kevesebb az egyenlet, mint az ismeretlenek száma), akkor az egyenletrendszer legfeljebb valamelyik ismeretlennek a többihez való arányait határozza meg (ezt sem föltétlenül egyértelműen). Esetünkben pl. lényegében az ac és bc arányokat határoztuk meg.
 

II. megoldás: Jelöljük a keresett arányt x-szel, akkor m, n és x között keresünk egy (a-tól, b-től és c-től független) összefüggést. Ha ez sikerül, abból x-et már kifejezhetjük. Az m, n és x-re fennáll
m=b+ca,n=c+ab,x=a+bc.(1)

Az egyenletek szimmetriáját a, b és c-ben még világosabbá tehetjük, ha mindegyik egyenlőséghez hozzáadunk 1-et:
m+1=a+b+ca,n+1=a+b+cb,x+1=a+b+cc.
Innen, ha m, n és x egyike sem -1, akkor
1m+1+1n+1+1x+1=a+b+ca+b+c=1,
amiből x-re az
x=m+n+2mn-1
érték adódik, ha mn≠1.
Ha mn=1, akkor az (1) alatti első két egyenlet szorzatából
1=ab+c(a+b)+c2ab=1+c(a+b+c)ab
Innen, mivel feltettük, hogy a, b, c egyike sem 0, következik, hogy
a+b+c=0,(2)
s így
m=n=x=-1.

Ugyancsak a (2) egyenlethez jutunk, ha m, n és x közül csak egyről tesszük fel, hogy értéke -1.
 

2. feladat.
 

I. megoldás: A megoldók egy része számítással igazolta az állítás helyességét. Bemutatunk egy ilyen megoldást. Legyen a P pont távolsága az AB és CD oldaltól 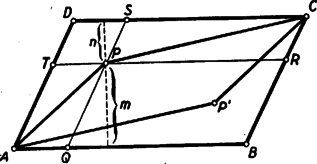m, ill. n (1. ábra).
 
 
1. ábra
 

Az APCP' paralelogramma t területét megkapjuk, ha az ABCD paralelogramma területéből elhagyjuk az ABCP' és APCD négyszögek területét.
Az utóbbi két terület egyenlő, mert az idomok egymás tükörképei az ABCD paralelogramma középpontjára nézve, így elegendő pl. az APCD négyszög területének kétszeresét vonni le. Ezt a négyszöget az APT és PCS háromszögekre, továbbá a PSDT paralelogrammára bontva, azt kapjuk, hogy
t=AB⋅(m+n)-AQ⋅m-QB⋅n-2AQ⋅n=(AQ+QB)(m+n)--AQ⋅m-QB⋅n-2AQ⋅n=QB⋅m-AQ⋅n.


Itt a kisebbítendő a PRBQ paralelogramma területét, a kivonandó pedig a PSDT paralelogrammáét adja. Ezzel igazoltuk a feladat állítását.
 

Megjegyzés. Az ábrán P az ACD háromszögben van. Ez esetben az APCD négyszög konkáv. Ha az ABC háromszögben levő P pontból indulunk ki, akkor számításunk negatív jellel adja a kiszámítandó paralelogramma területét, annak megfelelően, hogy az említett négyszög ez esetben konvex, és tükörképével együtt kétszeresen fedi az APCP' paralelogrammát.
Számítás nélkül, közvetlenül is belátható a feladatban szereplő területek egyenlősége. A következőkben erre mutatunk két utat.
 

II. megoldás: Húzzunk P' ponton át AB-vel és BC-vel párhuzamos egyenest, és messék ezek BC-t, ill. AB-t az R' és Q' pontban.
Az APCP' paralelogrammát körülzáró két konkáv négyszög egyikét, pl. az AP'CB négyszöget vágjuk szét az AP'Q' és P'CR' háromszögre, valamint a P'R'BQ' paralelogrammára (2. ábra).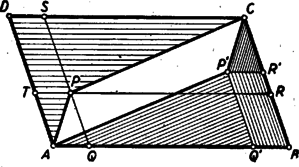
 
 
2. ábra
 

Fedjük le az AP'Q' háromszöggel a PCR háromszöget. (AP'Q'▵=PCR▵, mert AP'=PC és a két háromszög szögei egyenlők.) Továbbá a P'CR' háromszöggel lefedjük APQ háromszöget, a P'R'BQ' paralelogrammával pedig a PTDS paralelogrammát (3. ábra).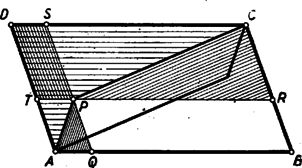
 
 
3. ábra
 

Ezek után az ABCD paralelogrammából a két konkáv négyszöggel lefedetlen marad a PRBQ paralelogramma, kétszeresen fedett a PSDT paralelogramma. Ezért
TAPCP'=TPRBQ-TPSDT
 

III. megoldás: Messe a TR egyenes az AC átlót a P∘ pontban. Húzzunk P∘ ponton át AD-vel párhuzamos egyenest, mely AB-t Q∘-ban, CD-t pedig S∘-ban metszi (4. ábra).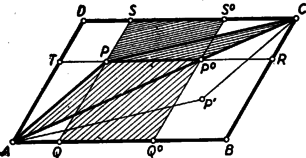
 
 
4. ábra
 

Kimutatjuk, hogy az APCP' paralelogramma területe egyenlő a QQ∘S∘S paralelogramma területével, és ugyanezzel egyenlő a PQBR és PSDT paralelogrammák területének különbsége is.
PP∘C△ területe fele a PP∘S∘S paralelogramma területének, mert PP∘ oldaluk és ehhez tartozó magasságuk megegyezik. Hasonló okból PP∘A△ területe fele a PP∘Q∘Q paralelogramma területének. Eszerint az APCP' paralelogramma területe, mely az APC△ területének kétszerese, valóban egyenlő a QQ∘S∘S paralelogramma területével.
Ismeretes továbbá, hogy
TP∘S∘DT=TP∘Q∘BR.
De
TP∘S∘DT=TPSDT+TP∘S∘SP,
és
TP∘Q∘BR=TPQBR-TP∘PQQ∘.
E három egyenlet alapján
TPQBR-TPSDT=TP∘S∘SP+TP∘PQQ∘=TQQ∘S∘S,
és ezzel állításunk második részét is bebizonyítottuk.
Ha (az ábrától eltérőleg) a P pont az ABC△ belsejébe esik, akkor az előbbi gondolatmenettel arra jutunk, hogy
TAPCP'=TQQ∘S∘S=TPSDT-TPQBR.

Megemlítjük, hogy egyes versenyzők a területeket szerkesztéssel négyzetekké alakították, és ezeket hasonlították össze. Területek szemlélettel, vagy méréssel történő összehasonlítása nem tekinthető bizonyító erejűnek!
 

3. feladat.
 

I. megoldás: Az ABDE trapéz egyenlő szárú, mert átlói egyenlők. Tehát az egyíves szögek egyenlők. Hasonló ok miatt a kétíves szögek is egyenlők, éppígy a háromívesek is (1. ábra).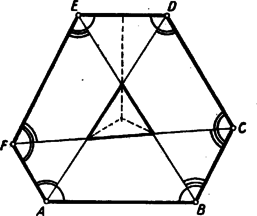
 
 
1. ábra
 

CDEF négyszög húrnégyszög, mert a szemközti szögeinek összege egyenlő (mindkét szemközti szögpár egy egyíves, egy kétíves és egy háromíves szögből tevődik össze). Azonban e húrnégyszög körén van a B pont is, mivel EBC∢=EFC∢. Az A pont szintén ezen a körön van, mivel FAD∢=FCD∢.
 

Megjegyzés: Több versenyző állította, hogy az ABDE, BCEF és CDFA húrnégyszögek két-két csúcsa közös lévén, ebből máris következik, hogy a köré írt körük is egybeesik. Ez nem igaz.
 

II. megoldás: ABDE egyenlőszárú trapéz, ezért a párhuzamos oldalak felező merőlegese közös, átmegy a két átló metszéspontján és egyenlő szöget zár be a két átlóval. Eszerint a hatszög szemközti oldalainak felező merőlegesei egyben az átlók alkotta háromszög szögfelezői, tehát egy pontban metszik egymást. Ez a pont egyenlő távolságra van a hatszög bármely négy szomszédos pontjától (mint a három felező merőleges metszéspontja), így tehát egyenlő távolságra van mind a hat csúcstól. Eszerint a hatszög köré kör írható, és a kör középpontja az egyenlő átlók alkotta háromszög szögfelezőinek metszéspontja.
 

Megjegyzés. 1. Tételünk hurkolt hatszögre is fennáll (2. ábra).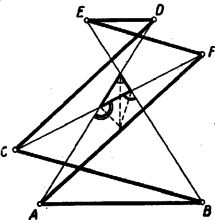
 
 
2. ábra
 

Hurkolt hatszög esetében a hatszög köré írható kör középpontja az egyenlő átlók alkotta háromszög két külső és egy belső szögfelezőjének metszéspontja (tehát a háromszög egyik hozzáírt körének középpontja).
Számos versenyző hibásan úgy vélte, hogy a feladat követelményeinek csak oly hatszög felelhet meg, amelynek átlói egy pontban metszik egymást, sőt egyesek szerint a hatszög csak szabályos lehet.