1. feladat. Oldjuk meg a következő egyenletet:

(ha  n4l+1  alakú és  s=l=n-14). Ezekben az esetekben ${90}^{\circ }$ az egyenletnek kétszeres gyöke.

 

2. feladat. Legyen $a$ és $b$ egész szám. Bizonyítandó, hogy

$\begin{array}{c}{\displaystyle x^2+ax+b}\end{array}$

csak akkor állíthat elő végtelen sok egész $x$-értékre négyzetszámot, ha a kifejezés egy elsőfokú polinom négyzete.

 

I. megoldás: Azt kell vizsgálnunk, mikor állhat fenn egész $x$, $y$ értékekre

$\begin{array}{c}{\displaystyle x^2+ax+b=y^2\mathrm{.}}\end{array}$

Innen $x$-et meghatározva

$\begin{array}{c}{\displaystyle x=\frac{-a\pm \sqrt[]{a^2-4b+4y^2}}{2}\mathrm{,}}\end{array}$

(1)

és ez csak úgy adhat egész értéket, ha a négyzetgyökjel alatt teljes négyzet áll:

$\begin{array}{c}{\displaystyle a^2-4b+4y^2=z^2}\end{array}$

Innen

$\begin{array}{c}{\displaystyle z^2-4y^2=\left(z+2y\right)\left(z-2y\right)=a^2-4b\mathrm{.}}\end{array}$

A jobb oldalon állandó érték áll; így ha $y$ is, $z$ is természetes szám, akkor ez az egyenlőség csak olyan értékekre állhat fenn, amelyekre $2y+z$ nem nagyobb ennél az állandó értéknél. Ilyen $y$, $z$ számpár csak véges sok van. Minden $y$ értékhez (1) szerint legfeljebb két $x$ érték tartozik, tehát csak véges sok olyan egész $x$ érték lehet, amelyre $x^2+ax+b$ négyzetszám, ha $a^2-4b\ne 0$.
Ha viszont $a^2-4b=0$, akkor

$\begin{array}{c}{\displaystyle x^2+ax+b=x^2+ax+{\left(\frac{a}{2}\right)}^2={\left(x+\frac{a}{2}\right)}^2\mathrm{,}}\end{array}$

tehát a kifejezés egy elsőfokú polinom négyzete. Ezzel igazoltuk a feladat állítását.

 

Megjegyzés: A tárgyalt második esetben $b=\frac{a^2}{4}$ csak úgy lehet egész szám, ha $a$ páros. Ebben az esetben az adott másodfokú kifejezés egy egész együtthatós elsőfokú polinom négyzete, s így minden egész $x$ értékre négyzetszámot állít elő.

 

II. megoldás: Kényelmesebb lesz az adott kifejezés négyszeresét vizsgálni. Ez is négyzetszámot állít elő, ha az adott polinom értéke négyzetszám, de fordítva is: a polinom egész helyen mindig egész számot állít elő, s így $a$ négyszerese mindig páros számot. Ha ez a néggyel szorzott érték négyzetszám, akkor páros szám négyzetének kell lennie, s így a negyedrésze, vagyis az eredeti polinom értéke is egész szám négyzete. Elegendő tehát a polinom négyszeresét vizsgálni:

$\begin{array}{c}{\displaystyle 4x^2+4ax+4b={\left(2x+a\right)}^2+4b-a^2\mathrm{.}}\end{array}$

Ha ez egy $y$ egész szám négyzete, akkor

$\begin{array}{c}{\displaystyle 4b-a^2=y^2-{\left(2x+a\right)}^2=\left(y+2x+a\right)\left(y-2x-a\right)\mathrm{.}}\end{array}$

Azonban egy egész szám a $0$ kivételével csak véges sok féleképpen bontható két egész szám szorzatára, egy-egy felbontás pedig már egyértelműen meghatározza $x$-et és $y$-t.
Így az adott kifejezés csak akkor vehet fel végtelen sok egész $x$ értékre négyzetszámot, ha $4b-a^2=0$, ekkor

$\begin{array}{c}{\displaystyle 4x^2+4ax+4b={\left(2x=a\right)}^2}\end{array}$

és ennek negyedrésze ugyancsak egy elsőfokú polinom négyzete. Ezzel igazoltuk a feladat állítását.

 

Megjegyzés: Mint láttuk, ha végtelen sok helyen állít elő a polinom négyzetszámot, akkor minden egész $x$-re négyzetszám az értéke, tehát eredményünk így fogalmazható: ha egy a feladatban adott alakú polinom értéke minden egész $x$-re négyzetszám, akkor a polinom egy polinom négyzete. Ez az állítás már sokkal általánosabban igaz, nemcsak a legmagasabb fokú tagnak adhatunk együtthatót, hanem a fokszámra sem kell kikötést tennünk. Érvényes a következő tétel: Ha egy egész együtthatós polinom értéke minden egész helyen négyzetszám, akkor a polinom egy polinom négyzete. A tétel négyzet helyett tetszés szerinti egész $k$-val $k$-adik hatványokra is igaz.
Az viszont lényeges, hogy ne csak végtelen sok egész helyre tegyünk feltételt, mert amint a legmagasabb együtthatóról nem kötjük ki, hogy $1$ legyen, akkor már van olyan másodfokú polinom is, amelyik nem teljes négyzet, és végtelen sok egész helyen vesz fel négyzetszámot értékül.

 

3. feladat. Alkossunk 6 csúcsú, 5 lapú poliédert a következő feltételekkel:
a) a poliéder egyik lapja $a$ oldalú négyzet;
b) a poliéder összes többi éle egyenlő egymással;
c) a négyzet két szomszédos oldalához csatlakozó két lapnak a négyzetlappal bezárt szöge egymást ${90}^{\circ }$-ra egészíti ki.
Bizonyítsuk be, hogy a poliéder két lapjának az átlói $a$ hosszúságúak.

 

Megoldás: A leírt test négyzetlapja legyen $ABCD$. A testnek van egy ennek valamelyik oldalával, mondjuk $AB$-val párhuzamos $EF$ éle, melynek merőleges vetülete a négyzet $AB$-vel párhuzamos középvonalára esik és azon szimmetrikusan helyezkedik el.

 

 

Legyen $F$ merőleges vetülete a négyzetlapon, a négyzet $AB$, ill. $BC$ oldalán rendre $F_1$, $G$ és $H$, jelöljük a négyzet oldalaitól különböző egyenlő élek hosszát $b$-vel, az $F{F}_1$ távolságot $m$-mel. Az $F{F}_1$ szakasz merőleges $F_{1}G$-re és $F_{1}H$-ra is, így az $F{F}_{1}G$ háromszöget beforgathatjuk körülötte az $EFH$ síkba, ekkor $G$ egy a $H{F}_1$ egyenesen fekvő $G_1$ pontba kerül. A c) feltétel szerint az $F{G}_{1}H$ háromszög $F$-nél derékszögű, $F{F}_1$ pedig a háromszög magassága. Így a magasságra vonatkozó középarányossági tétel szerint, mivel $F_{1}G=a/2$ és $F_{1}H=\left(a-b\right)/2$,

$\begin{array}{c}{\displaystyle m^2=\frac{a}{2}\cdot \frac{a-b}{2}\mathrm{.}}\end{array}$

(1)

Számítsuk ki az $ABFE$ trapéz $AF$ átlóját, mint a páronként merőleges $AG$, $G{F}_1$, $F_{1}F$ szakaszokból alkotható téglatest testátlóját. Az $EB$ átló és a $GDEF$ trapéz átlói szimmetria okokból ugyanekkorák. Felhasználva (1)-et is, azt kapjuk, hogy
${\displaystyle \begin{array}{c}\hfill {\displaystyle A{F}^2=A{G}^2+G{F}_1^2+F_1{F}^2={\left(\frac{a+b}{2}\right)}^2+{\left(\frac{a}{2}\right)}^2+m^2={\left(\frac{a+b}{2}\right)}^2+}\hfill \\ \hfill {\displaystyle +{\left(\frac{a}{2}\right)}^2+\frac{a\left(a-b\right)}{4}=\frac{1}{4}\left(3a^2+ab+b^2\right)\mathrm{.}}\hfill \end{array}}$


A feladat állításához azt kell tehát belátnunk, hogy $ab+b^2=a^2$. Az $a$ és $b$ élhosszak közt tudunk egy összefüggést kapni, ha felírjuk Pythagoras tételét $FB$-re, mint annak a téglatestnek átlójára, melynek egyik lapja $BG{F}_{1}H$ és egyik további csúcsa $F$. Felhasználva (1)-et is:

$\begin{array}{c}{\displaystyle b^2=F{B}^2=B{H}^2+H{F}_1^2+F_1{F}^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{a-b}{2}\right)}^2+\frac{a\left(a-b\right)}{4}=}\end{array}$

$\begin{array}{c}{\displaystyle =\frac{1}{4}\left(3a^2-3ab+b^2\right)\mathrm{.}}\end{array}$

A $b$-t tartalmazó tagokat a bal oldalra rendezve és $3$-mal osztva innen valóban

$\begin{array}{c}{\displaystyle ab+b^2=a^2}\end{array}$

adódik és ezzel igazoltuk a feladat állítását.

 

Megjegyzések: 1. Az utolsó egyenletből $b$-re két érték adódik: $a\left(\sqrt[]{5}-1\right)/2$ és $-a\left(\sqrt[]{5}+1\right)/2$. Mint egy versenyző, Kalmár Ágota, megjegyezte, a negatív gyöknek is lehet geometriai jelentést tulajdonítani. Ennek egy önmagát átmetsző test felel meg: a két háromszöglap áthatol egymáson, a másik két oldallap pedig hurkolt trapéz lesz $a\left(\sqrt[]{5}+1\right)/2$ oldalhosszúsággal.

 

 

Ugyanekkora az alaplappal párhuzamos él is, míg a trapézok átlói (amelyek most a hurkolt trapézon kívül húzódnak) $a$ hosszúságúak.
2. Helyezzük a feladatban szereplő testet egy kocka fölső vízszintes $ABCD$ lapjára ($EF$ legyen $AB$-vel párhuzamos), majd az $ABRS$-re is helyezzük el a test egy példányát úgy, hogy az $EF$-nek megfelelő él $AS$-sel legyen párhuzamos. Ekkor az $AB$-hez csatlakozó háromszög és trapéz lap a lapszögekre tett kikötés szerint egy síkba esik és egy egyenlő oldalú ötszöget alkot, amely az $EF$ felezőmerőlegesére szimmetrikus. A többi kockalapokra is elhelyezhetjük a test egy-egy példányát úgy, hogy egy $12$ egybevágó, egyenlő oldalú ötszög határolta poliédert kapjunk. Belátható (erre még visszatérünk), hogy a kapott test egy szabályos dodekaéder.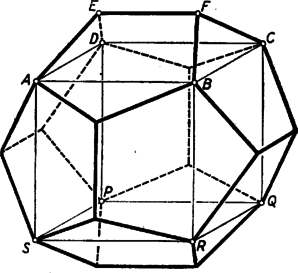

 

 

---

¹Ez könnyen igazolható, ha a bal oldalon $\alpha$-t és $\beta$-t a jobb oldalon szereplő szögek összege, illetőleg különbségeként írjuk.