Cím: Az 1958. évi Országos Matematikai Tanulmányi Verseny: 1. közlemény: az I. forduló és az ott kitűzött feladatok megoldása
Füzet: 1958/szeptember, 1. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny első fordulója ez évben ‐ mint tavaly is ‐ március 20-án folyt le az egyes iskolákban, és azon a gimnáziumok és ipari technikumok III. és IV. osztályú tanulói vehettek részt, az előző évi versennyel azonos feltételek mellett. A dolgozat elkészítésére 5 óra állott rendelkezésre. Beadtak 252 iskolában 1951 dolgozatot. Tavaly 229 iskolában 3104 dolgozatot adtak be, tehát ez évben több iskola vett részt a versenyben, de a beadott dolgozatok száma csökkent. Az iskolák számának emelkedését a gimnáziumok számának növekedése okozta, 209-re nőtt számuk, szemben a tavalyi 179-cel. A technikumok száma csökkent: 45-ről 43-ra. A versenyzők számának csökkenését a versenyre bocsátás mértékének szigorítása okozta.
A központi versenybizottság április 22-i javaslata alapján 142 iskola 323 tanulója ‐ a dolgozat-beadók 16,6%-a ‐ került a II. döntő fordulóba (tavaly 10,4%).
Részletes adatokat iskolafajok, megyék és városok szerint a táblázat közöl.

Kimulatás az 1958. évi Országos Matematikai Verseny I. fordulójárólBeadott dolgozatokDöntőbe kerültMegyék és városokgimnáziumip.technikumösszesengimnáziumip.technikumösszeseniskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanuló   1. Baranya419--41945--45I. Pécs4302226521125362. Bács-Kiskun   1171141275610127123. Békés1084112119648--484. Borsod666--66635--35II. Miskolc város4434488912623495. Csongrád630--63039--39III. Szeged város33131764849--496. Fejér64611476023--237. Győr-Sopron118531814103510--5108. Hajdú-Bihar526--52622--22IV. Debrecen638349424811599. Heves447--4474111151210. Komárom6361173735--3511. Nógrád281431212112312. Pest1259--12591120--112013. Somogy5451364848--4814. Szabolcs1157--115766--6615. Szolnok131011814109810--81016. Tolna852--852914--91417. Vas946--94644--4418. Veszprém9891101099717--71719. Zala220111331--1111Vidék157112924176181130597173914106187V. Budapest*49463191836864641114122253136Összesen20615924335924919511382872136159323*A gimnáziumokhoz sorolva 1 katonai középiskola 12 versenyzővel, akik közül 3 bekerült a döntöbe.

A döntőbe került 323 tanuló közül 189 (58,5%) lapunk feladatmegoldója (tavaly 58,3%).
A tavalyi versenyen helyezést nyert 29 III. osztályos tanuló közül 23 bekerült a döntőbe, a múlt évi Arany Dániel versenyen helyezést elért 32 II. osztályú tanuló közül 24 az idén is a döntőbe jutott.
Alább közöljük az I. fordulón kitűzött 3 feladatot megoldásokkal és megjegyzésekkel.
 

1. feladat. Legyen a1, a2, ..., an an+1 különböző elemekből álló számtani sorozat. Írjuk egyszerű alakban az
Sn=xa22-a12+xa32-a22+...+xan+12-an2
összeget, ha x≠1.
 

Megoldás: Az a1, a2, ..., an+1 számtani sorozat különbségét d-vel jelölve, a kitevőket átalakítjuk:
a22-a12=(a2-a1)(a2+a1)=d(a2+a1)=d(2a1+d)=2a1d+d2,
hasonlóan:
a32-a22=2a1d+3d2,⋅⋅⋅an+12-an2=2a1d+(2n-1)d2,


úgy, hogy:
Sn=x2a1d+d2+x2a1d+3d2+...+x2a1d+(2n-1)d2==x2a1d+d2(1+x2d2+x4d2+...+x(2n-2)d2).


A zárójelben olyan n tagú mértani sor áll, amelynek hányadosa x2d2. Mivel a feltétel szerint x≠1 és d≠0, azért a hányados nem 1, és így alkalmazhatjuk a mértani sor összegképletét, amely szerint:
Sn=x2a1d+d2⋅x2nd2-1x2d2-1.

2. feladat. Keressünk olyan pozitív egész számot, amelynek utolsó jegye 2, és ha ezt a jegyet a szám végéről elhagyva az elejére írjuk, akkor a szám kétszeresét kapjuk.
 

I. megoldás: Ha a keresett szám utolsó jegye 2, akkor kétszerese csak 4-re végződhet. Ez lesz a keresett szám utolsó előtti jegye is. Ennek kétszerese 8, a szám kétszeresének lesz utolsó előtti jegye, így a keresett számnak végétől számított harmadik jegye is 8 kell hogy legyen. A szám kétszeresének végétől számított harmadik jegye 6, mivel 8 kétszerese 6-ra végződik. A keresett számnak tehát 6 lesz a végéről számítandó negyedik jegye. A számból így már megvan: ...6842. Ennek kétszeresét képezve a negyedik jegy egyúttal a keresett számból a 2 elhagyásával és elejére írásával keletkező számnak is hátulról számított negyedik jegye lesz. Ez a jegy 3, mivel a 6 kétszereséhez a 2⋅8-nak 1-es maradékát is hozzá kell számítanunk. Így haladhatunk tovább a keresett szám számjegyeinek megállapításában.
A feladatnak megfelelő legkisebb számot akkor kapjuk meg, amikor a kétszeres számban először jutunk 2-höz. Ezen az úton a
105263157894736842=A
számhoz jutunk, amire ismét alkalmazva az eljárást 2A első jegyéül 2 adódik. Ezt tekinthetjük az utolsó jegy előreírásából keletkezőnek, s így A megoldása a feladatnak, mégpedig a legkisebb megoldása.
Folytathatjuk azonban tovább is az eljárást az 1 elé írva egy 2 számjegyet; ez esetben újra az A jegyei ismétlődnének s így kapjuk egy további megoldásként az A⋅1018+A számot, és hasonlóan ismételhetjük A jegyeit periodikusan akárhányszor, mindig megoldást kapunk. Az eljárás, amivel ezeket a megoldásokat nyertük, mutatja, hogy csak ezek a megoldások lehetségesek. A feladat összes megoldásai tehát az

A⋅1018k+A⋅1018(k-1)+...+A⋅1018+A=A⋅1018(k+1)-11018-1(k=0,1,2,...)


számok.
 

Megjegyzések: 1. A számjegyei között már korábban is előfordult a 2 (A negyedik jegye), ott azonban nem állhattunk meg, mert a szám kétszerezésével akkor a 2 elé egy 1 kerül.
2. Kezdhettük volna a számjegyek megállapítását a szám elejéről is: kétszerezéssel a szám elejére 2 csak úgy kerülhet, ha első jegye 1, viszont 21 csak úgy, ha az után 05 következik stb.
3. Sok megoldó megelégedett A megadásával, és nem adta meg az összes megoldást.
 

II. megoldás: Nevezzük a 2 elhagyása után megmaradó számot x-nek, és legyen ez n-jegyű szám. Ekkora keresett szám így írható: 10x+2. Ha a 2-t az x szám elé írjuk, akkor az így kapott szám 2⋅10n+x. A feltétel szerint tehát:
2(10x+2)=2⋅10n+x,
amiből:
x=2⋅10n-219
és az eredeti szám:
10x+2=20⋅10n-219+2=20⋅10n-219=10n+10n-219.(1)
Ezek akkor egész számok, ha 10n-2 osztható 19-cel, vagyis ha 10n osztva 19-cel maradékul 2-t ad. Ez azt jelenti, hogy ha elkezdve tizedes törtté alakítani az 119 számot, az osztási maradékok közt előfordul a 2, akkor van a feladat feltételeinek megfelelő szám, egyébként nincs, ilyen számot úgy kapunk, hogy vesszük a 2 maradék föllépéséig nyert hányadost, tizedesvessző kitétele nélkül és ha az n-edik 0 ,,levétele'' után lépett fel a 2 maradék, akkor az így kapott egész számhoz 10n-t adunk hozzá.
Az osztást elvégezve a 17-ik 0 levétele után lép fel először 2 maradékul és ekkor a hányados 5 263 157 894 736 842, tehát a keresett szám nyomán megfelel 105 263 157 894 736 842. Ha az osztásban nem állunk meg a ,,2'' maradéknál, akkor a hányados következő jegyéül 1-et és maradékul is 1-et kapunk, tehát innen ismétlődnek az eddig nyert maradékok és a hányadosban az eddig nyert jegyek, leírva a következő 0 levételekor keletkező 0 jegyet is. Így bármeddig folytatva az osztást, az első ,,2''-től kezdve minden tizennyolcadik lépés újra ,,2'' maradékhoz vezet. Ezek bármelyikénél megállhatunk.
Ezen az úton megkapjuk az előző megoldásban nyert összes számokat, amelyek megfelelnek a feladat követelményeinek.
 

Megjegyzés: Az 119 tizedes törtté alakításának megfelelő osztás közben 1-től 18-ig minden szám előfordul maradékként, így a 19 tehát ún. főnix nevező1. Az azonban, hogy a feladat megoldható ‐ azaz, hogy előfordult a maradékok között a 2, ‐ ez nem azon múlik, hogy minden lehetséges maradék tényleg fellépett. Ha pl. azt követelnénk, hogy a szám az utolsó jegy előrehelyezésével 5-szörösére vagy 7-szeresére változzék, ebből arra a követelményre jutnánk, hogy az 149 osztás közben az 5, ill. az 169 osztás közben a 7 maradék fellépjen és mindkettő be is következik, bár sem a 49, sem a 69 nem főnix nevező (összetett szám nem is lehet az).
 

3. feladat. Rajzoljunk egy háromszög oldalai fölé kifelé négyzeteket. Bizonyítsuk be, hogy a négyzeteknek a háromszögcsúcsoktól különböző csúcsai olyan hatszöget határoznak meg, amelynek minden második oldala a háromszög egy-egy súlyvonalának a kétszerese.
 

I. megoldás: Legyenek a B-ből induló és AB-re, illetve BC-re merőleges négyzet oldalak BD és BE. Forgassuk el a BDE háromszöget B körül 90∘-kal úgy, hogy E a C pontba kerüljön. Ekkor BD az AB oldal meghosszabbításába kerül és azzal egyenlő BD1 szakaszt alkot.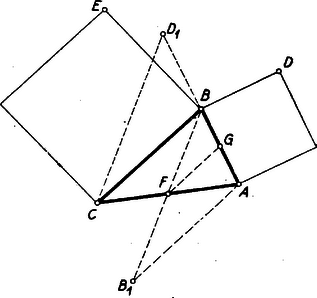
 
 
1. ábra
 

Ennek folytán, ha meghúzzuk az ABC háromszög B-ből induló BF súlyvonalát, az egyben az ACD1 háromszög középvonala is lesz, s így az ED-vel egyenlő CD1 szakasz a BF súlyvonal kétszerese, a feladat állításának megfelelően. Hasonlóan járhatunk el a hatszög másik két szóbajövő oldalával is.
 

Megjegyzések: 1. Azt is tudjuk, hogy BF párhuzamos a CD1 oldallal, s így ED, amiből CD1 egy 90∘-os elforgatással keletkezett, merőleges is a BF súlyvonalra.
Nem egy versenyző észrevette ezt a merőlegességet, de sajnos, fennállását a szemléletből, bizonyítás nélkül elfogadta, holott ez a tény semmivel sem magátólértetődőbb, mint aminek bizonyítását a feladat kívánja.
2. Számos megoldás a fentinek nem lényegesen különböző változata. Így egyesek a B pont F-re vonatkozó B1 tükörképét véve a BDE és ABB1 háromszögek egybevágóságát igazolták, vagy meghúzva a BC-vel párhuzamos FG középvonalat, a BFG és DEB háromszögek hasonlóságát bizonyították fentiekkel rokon gondolatok alapján.
 

II. megoldás: A D és E pontok jelentése legyen ugyanaz, mint az előző megoldásban, és a BDE háromszög B-ből induló magasságvonala messe AC-t F-ben.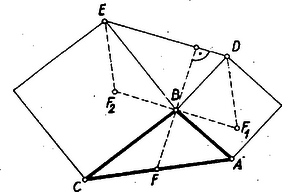
 
 
2. ábra
 

Forgassuk el az ABF és CBF háromszögeket B körül ellenkező irányban 90∘-kal úgy, hogy az A pont D-be, C pedig E-be kerüljön. A háromszögek új helyzete legyen DBF1 és EBF2.
Ekkor az elforgatás következtében a BF1 és BF2 szakaszok merőlegesek BF-re, s így egy egyenesbe esnek, amely párhuzamos ED-vel; másrészt DF1 és EF2 merőleges AC-re, tehát párhuzamos egymással.
Ezek szerint DEF2F1 paralelogramma. Ebből következik egyrészt, hogy DE egyenlő hosszú F1F2-vel, ami BF kétszerese; másrészt az AF-fel egyenlő hosszú DF1 és a CF-fel egyenlő EF2 egymással egyenlők, így tehát BF az ABC háromszög súlyvonala. Ezzel a feladat állítását igazoltuk.
 

III. megoldás: Jelölje D és E ugyanazokat a pontokat, mint az előző megoldásokban. Egészítsük ki az ABC és BDE háromszögeket az ABCB1, ill. BDB2E paralelogrammává.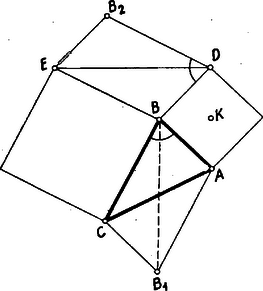
 
 
3. ábra
 

Azt állítjuk, hogy ez a két paralelogramma egybevágó. Forgassuk ugyanis el az ábrát az AB fölötti négyzet K középpontja körül 90∘-kal úgy, hogy AB a BD oldalba menjen át. Ekkor az AB1 oldal, amelyik párhuzamos és egyenlő BC-vel, az utóbbira merőleges BE négyzetoldalra kerül, tehát az ABCB1 paralelogramma BDB2E-t fogja fedni.
Az AC és DE oldalak ennek a paralelogrammának a két átlójával egyenlők s így a paralelogrammában felezik egymást. Ez azonban éppen azt jelenti, hogy a két háromszög bármelyikében a B-vel szemközti oldal a másik B-ből induló súlyvonalának a kétszerese és arra merőleges. Ezzel a feladat állítását (annál valamivel többet is) igazoltuk.
 

Megjegyzések: 1. Ebben a megoldásban világos az ABC és DBE háromszögek teljesen szimmetrikus szerepe, ami különben közvetlenül látszik abból, hogy az ábrán szereplő két négyzet keletkezhetett akár mint az egyik, akár mint a másik háromszög B-ből induló oldalaira kifelé rajzolt négyzet.
2. Ennek megfelelően az I. és II. megoldásban is felcserélhetnénk a két háromszög szerepét, ami annak felel meg, hogy ábráink alapján DE helyett AC-re is igazolhatnánk a feladatnak megfelelő állítást. Ez az I. megoldás esetén teljesen azonos módon történhetne, a II. megoldást annyiban kellene módosítani, hogy BF súlyvonal voltának bizonyítása helyett arra kellene hivatkoznunk, hogy a BDE háromszög B-ből kiinduló súlyvonala egyben a paralelogramma középvonala is, és így DF1-gyel és EF2-vel párhuzamos és egyenlő, a kettő együtt pedig kiadja AC-t.
3. A feladat állítása érvényben marad akkor is, ha nem kifelé, hanem ,,befelé'' rajzolunk az ABC háromszög oldalai fölé négyzeteket. (A hatszög ebben az esetben hurkolt hatszög lesz.) Ez esetben a bizonyításainkban szereplő BDE háromszög helyébe mindössze annak a B pontra vonatkozó tükörképe lép.
1Az ilyen számokról bővebb felvilágosítást ad pl. a következő mű: Péter Rózsa: A számok világa. (Budapest, 1948. Új Nevelés Könyvtára, 144. o.)