Cím: Megjegyzések egy versenyfeladathoz
Szerző(k):  Lőrincz Pál 
Füzet: 1958/december, 129 - 134. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1958. évi Arany Dániel haladók versenye döntőjének 3. feladatát és annak megoldását lapunk előző számában ismertettük. A versenyzőktől csak a szerkesztés végrehajtását kívántuk, ezért zártuk ki a háromszögek közül a tompaszögűeket. Mindamellett a közölt I. megoldás után rámutattunk arra a meglepő tényre, hogy bár a szerkesztés mindenkor egyértelműen elvégezhető, a kitűzött feladatnak mégis csak abban az esetben adja megoldását, ha az adott háromszög oldalai fölé befelé rajzolt szabályos háromszögek harmadik csúcsai az adott háromszöggel megegyező körüljárású háromszöget határoznak meg. Ebből az a tanulság, hogy valamely feladat megoldásainak megvizsgálásánál sohasem lehetünk eléggé körültekintők.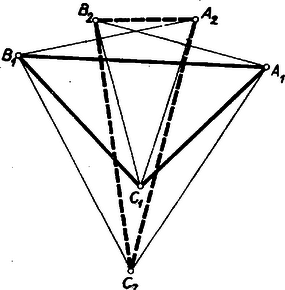
Az alábbiakban részletesebben foglalkozunk a feladat megoldhatóságának feltételével. Bemutatjuk, hogy a mélyebb diszkusszió milyen finom megfontolásokat igényel, és bár középiskolai matematikatudásunkkal elvégezhető, azonban újszerű, pontosabban szólva a középiskolában ritkábban használt módszerek alkalmazását kívánja.
Vizsgáljuk meg elsőnek, mi a feltétele annak, hogy egy adott A1B1C1 háromszög oldalai fölé befelé rajzolt A1B1C2, B1C1A2 és C1A1B2 szabályos háromszögekkel meghatározott A2B2C2 háromszög körüljárási értelme megegyezzék az A1B1C1 háromszög körüljárási értelmével (1. ábra).

 
 
1. ábra
 

Mindenekelőtt megjegyezzük, hogy ez nyilván csak az A1B1C1 háromszög szögeitől függ. Hiszen ha az A1B1C1 háromszög helyett egy ahhoz hasonló A1*B1*C1* háromszögből indulunk ki, akkor az ehhez tartozó ,,befelé rajzolt'' A2*B2*C2* háromszög szintén hasonló az A2B2C2 háromszöghöz, és A2*B2*C2* körüljárási értelme aszerint megegyező, ill. ellentétes az A2B2C2 körüljárási értelmével, amint az A1*B1*C1* és A1B1C1 háromszögek körüljárási értelem tekintetében megegyeznek, ill. ellentétesek.
Átmenetileg mégis szükségünk lesz adott háromszögünk oldalainak mértékszámára is. Tudjuk, hogy ezek aránya megegyezik a szemközti szögek szinuszainak arányával, és az arányossági szorzó csak a hosszmértékegység megválasztásától függ. Válasszuk úgy a mértékegységet, hogy az arányossági szorzó 2 legyen, vagyis ‐ ha az A1B1C1 háromszög szögeit rendre α-val, β-val és γ-val jelöljük ‐ legyen A1B1=2si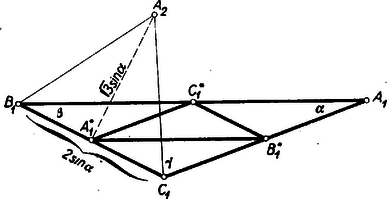nγ, B1C1=2sinα és C1A1=2sinβ (2. ábra).
 
 
2. ábra
 

Feltehetjük, hogy az A1B1C1 háromszög körüljárása az óramutató járásával ellenkező, azaz pozitív, továbbá, hogy α és β hegyesszögek, ugyanis bármely háromszög csúcsait lehet úgy megbetűzni, hogy e feltételek teljesüljenek.
Jelöljük A1B1, B1C1 és C1A1 felezőpontját rendre C1*, A1* és B1*-gal. Ekkor A1*B1*C1*▵∼A1B1C1▵, szögeik egyenlők, A1*B1*C1*▵ oldalai feleakkorák, mint az A1B1C1▵ oldalai, tehát A1*B1*=sinγ, B1*C1*=sinα és C1*A1*=sinβ, továbbá az A1*B1*C1*▵ körüljárási értelme ugyancsak pozitív.
Valamely háromszög körüljárási értelmének jellemzésére módot ad a koordináta-geometriának az a képlete, amely az illető háromszög területét csúcspontjainak koordinátáival fejezi ki:
2t=(x3-x2)y1+(x1-x3)y2+(x2-x1)y3,(1)
ismeretes ugyanis, hogy ez a képlet pozitív, ill. negatív előjellel adja meg a háromszög területét aszerint, amint a csúcspontoknak az 1, 2, 3 sorrendben való körüljárása pozitív, ill. negatív.
Hogy ezt vizsgálatunkban alkalmazhassuk, helyezzük el A1*B1*C1* háromszögünket a koordináta-rendszerben úgy, hogy A1* és B1* az X tengelyre; C1* pedig az Y-tengelyre essék; ha B1* jobbra van A1*-tól, akkor C1* az A1*B1*C1* háromszög pozitív körüljárási értelme folytán az Y-tengely pozitív felére jut (3. ábra).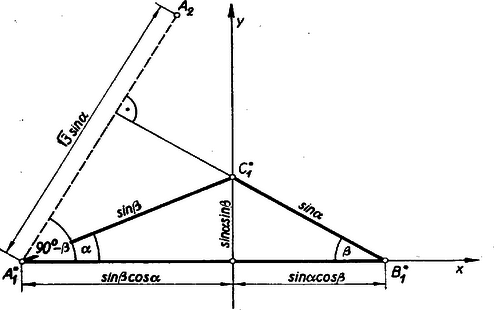
 
 
3. ábra
 

A csúcsok koordinátái az oldalak fenti mértékszámaival és a szögekkel kifejezve:
A1*(-sinβcosα,0),B1*(sinαcosβ,0),C1*(0,sinαsinβ).

Írjuk fel ezután az A2B2C2 háromszög csúcspontjainak koordinátáit ! Pl. az A2 pontot úgy nyerjük, hogy A1*-ból merőleges félegyenest bocsátunk B1*C1*-ra, és erre A1*-tól kezdve rámérjük a 2sinα oldalú szabályos háromszög magasságát, 3sinα-t (2. ábra). Így A2, B2 és C2 koordinátái a 3. ábráról:
A2(3sinαsinβ-sinβcosα,3sinαcosβ),B2(-3sinαsinβ+sinαcosβ,3sinβcosα),C2(0,-3sinγ+sinαsinβ),
figyelembe véve, hogy sin(90∘-α)=cosα és cos(90∘-α)=sinα. Ezekkel kifejezve az A2B2C2▵ kétszeres területét, 2t>0 azt fejezi ki, hogy az A2B2C2▵ körüljárási értelme pozitív, tehát megegyezik az A1*B1*C1* körüljárási értelmével.
(1) szerint tehát kell, hogy fennálljon:
2t=(3sinαsinβ-sinαcosβ)3sinαcosβ+(3sinαsinβ--sinβcosα)3sinβcosα+(-3sinαsinβ+sinαcosβ--3sinαsinβ+sinβcosα)(-3sinγ+sinαsinβ)>0.

A kijelölt műveletek elvégzése után a sin2α+cos2α=1 és a sinαcosβ+cosαsinβ=sin(α+β)=sin[180∘-(α+β)]=sinγ azonosságok felhasználásával egyenlőtlenségünk a következő alakra hozható:
10sinαsinβsinγ>3(sin2α+sin2β+sin2γ).(2)

Ez a kitűzött feladat megoldhatóságának feltétele. Eszerint bármely adott A1B1C1 háromszögről számítás útján megállapíthatjuk, hogy a belőle a fentiek szerint előálló A2B2C2 háromszög körüljárási értelemben megegyező-e vele vagy sem.
A (2) feltétel α, β és γ-ban szimmetrikus, ezért akkor is érvényes, ha α vagy β nem hegyesszög.
 

*
 

További érdekes kérdés: milyen határok közé esnek maguk a szögei a (2) feltételnek eleget tevő háromszögeknek ? Hogy erre megfelelhessünk, avégett ‐ szimmetriáját feláldozva ‐ olyan új alakot adunk (2)-nek, amelyben csak az α szög, továbbá a másik két szög β-γ különbsége szerepel.
A továbbiakban feltesszük, hogy β nem kisebb γ-nál, azaz β≥γ.
Vonjunk le (2) mindkét oldalából 23sinβsinγ-t:
(5sinα-3)2sinβsinγ>3[sin2α+(sinβ-sinγ)2].(3)
Itt a baloldalon
2sinβsinγ=cos(β-γ)-cos(β+γ)=cos(β-γ)+cosα,(3b)
és ez a kifejezés pozitív, mert sinα és sinβ pozitív. A jobboldalon ismert azonosságok felhasználásával a következő átalakításokat végezhetjük:
(sinβ-sinγ)2=2cos2β+γ2⋅2sin2β-γ2==[1+cos(β+γ)][1-cos(β-γ)]=(1-cosα)[1-cos(β-γ)].(3j)


Ezeknek (3)-ba való beírása után minden tagot az egyenlőtlenség baloldalára gyűjtve:
(5sinα-3)[cosα+cos(β-γ)]-3{sin2α+(1-cosα)[1-cos(β-γ)]}>0.(4)



Jelöljük most már a bal oldalon álló két változós függvényt ‐ a szokásos módon ‐ f(α,β-γ)-val:
f(α,β-γ)=(5sinα-3)[cosα+cos(β-γ)]-3{sin2α+(1-cosα)[1-cos(β-γ)]}(5)


és vizsgáljuk meg értékváltozását, pontosabban a 0-hoz való nagyságviszonyát, azaz előjelét α és β-γ különböző értékei mellett.
Foglalkozzunk először a β=γ esettel, azaz szorítkozzunk egyenlőszárú háromszögekre. Ekkor cos(β-γ)=1, tehát
f(α,β-γ)β=γ=(5sinα-3)(cosα+1)-3sin2α,
és ez csak α-nak függvénye. Hogy előjeléről tájékozódhassunk, számítsuk ki először 0-helyeit, vagyis az
(5sinα-3)(cosα+1)-3sin2α=0
egyenlet gyökeit. A második tagban sin2α=(1+cosα)(1-cosα) helyettesítés után kiemelhető az 1+cosα tényező, és ezzel az egyenletet oszthatjuk, mert ez csak α=180∘-nál válik 0-vá, amely esetben már nem jön létre háromszög. Az így adódó
5sinα-3-3(1-cosα)=0
egyenletet sinα=1-cos2α helyettesítés után az ismert módon megoldva, a következő gyököket nyerjük:
cosα1=1314;sinα1=3314,α1=21∘47,2';cosα2=-12,sinα2=32,α2=120∘.
A két gyök, α1 és α2, a 0<α<180∘ intervallumot három részre osztja. Helyettesítésekkel meggyőződhetünk arról, hogy
0<α<α1ésα2<α<180∘eseténf(α,β-γ)β=γ<0,
viszont
α1<α<α2eseténf(α,β-γ)β=γ>0(6)
(pl. cosα'=0,96 (egyben α'=0,28) mellett 0<α'<α1 és
f(α',β-γ)β=γ=2,744-2,03843<0; cosα''=0 (egyben sinα''=1) mellett f(α'',β-γ)β=γ=5-23>0;
cosα'''=-32 (egybensinα=12) mellett f(α''',β- -γ)β=γ=4-532<0, tehát β=γ esetén a (4) egyenlőtlenség a középső intervallumra teljesül, a két szélsőre nem, vagyis az α szög (és természetesen β és γ is) csak 21∘47,2' és 120∘ közötti értékeket vehet fel.
Mi a helyzet, ha β≠γ ? Látjuk, hogy (3) jobb oldala pozitív, és miután (3) bal oldalának (3b) második tényezője szintén pozitív, kell, hogy az első tényező, 5sinα-3 is pozitív legyen. Ha már most (4)-ben rögzítjük α értékét és (β-γ)-t változtatjuk, az így létrejött egyenlőtlenségek közül a ,,legerősebb'' egyenlőtlenség ‐ amelyben a két oldal különbsége a legnagyobb ‐ éppen β=γ-hoz tartozik, ugyanis β-γ növelésével cos(β-γ) csökken, a kisebbítendő csökken, a (pozitív) kivonandó növekszik, tehát a különbség csökken, az egyenlőtlenség ,,gyengül''. Eszerint β≠γ esetén sem nyerhetünk α-ra (6)-nál tágabb határokat, hiszen bármely f(α,β-γ)β≠γ>0 esetben fennáll a nála erősebb f(α,β-γ)β=γ>0 egyenlőtlenség is. Ez utóbbiról azonban megállapítottuk, hogy csak a (6) intervallumra teljesül.
Az, hogy α a (6) intervallumba tartozzék, a legutóbbiak szerint csupán szükséges feltétele (4), ill. (2) teljesülésének; vagyis ha α nem a (6)-ból való, akkor semmiesetre sem állhat, ellenben lehetséges, hogy valamely (6)-beli α és ,,elég nagy'' β-γ esetén (4) nem teljesül.
 

*
 

Állapítsuk meg végül, hogy milyen határok közti a mellett áll fenn α (4) egyenlőtlenség β és γ minden lehetséges értékpárjára.
A következőkben jelentse α a háromszög legkisebb szögét [α≤60∘ és (6) szerint α>21∘47,2']. Ahogyan a (4) egyenlőtlenség akkor a legerősebb, ha β-γ a lehető legkisebb, hasonlóan akkor a leggyengébb, ha β-γ a lehető legnagyobb. Adott α mellett ez akkor következik be, ha γ egészen α-ig csökken: γ=α. Ekkor β=180∘-2α, β-γ=180∘-3α. Ha az adott α-hoz tartozó leggyengébb f(α,β-γ)β-γ=180∘-3α>0 egyenlőtlenség fennáll, akkor a β és γ szögek α és 120∘ között bármely olyan értékpárt felvehetnek, amelyre teljesül α+β+γ=180∘ és β≥γ≥α. Vizsgáljuk tehát, hogyan változik az (5)-ből β-γ=180∘-3α -val adódó, és így csak α-tól függő
f(α,β-γ)β-γ=180∘-3α=(5sinα-3)[cosα+cos(180∘-3α)]-(7)-3{sin2α+(1-cosα)[1-cos(180∘-3α)]}


előjele, mely α értékekre lesz pozitív.
Ismert azonosságok alapján
cos(180∘-3α)=-cos3α=-cos(2α+α)==(sin2α-cos2α)cosα+2sin2αcosα=(2sin2α-1)cosα++2sin2αcosα=4sin2αcosα-cosα.


Ezt (7)-be behelyettesítve a műveletek elvégzésével és a sin2α+cos2α=1 azonosság felhasználásával függvényünk a következő alakú lesz
f(α,β-γ)β-γ=180∘-3α=2sin2α[10sinαcosα-3(sin2α+3cos2α)].
A 0-helyek kiszámítására szolgáló egyenletünket oszthatjuk 2sin2αcos2α-val, mert e szorzat a
21∘47,2'<α≤60∘(8)
intervallumban nem 0. Az így adódó
10tgα-3tg2α-33=0
egyenletnek (8)-ban egyetlen gyöke
tgα=13-bólα=30∘,
és behelyettesítéssel megállapíthatjuk, hogy az f(α,β-γ)β-γ=180∘-3α>0 egyenlőtlenséget az α>30∘ értékek elégítik ki.
Ebből az következik, hogy (4), és így (2) is, minden esetben fennáll, ha a háromszögnek mind a három szöge 30∘ és 120∘ közé esik. Ez tehát elegendő feltétele az eredeti feladat megoldhatóságának, ezt közöltük múlt számunkban az I. megoldás megjegyzésében.