Cím: 1957.évi Kürschák József matematikai tanulóverseny feladatainak megoldása
Szerző(k):  Hajós György 
Füzet: 1958/február, 38 - 46. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Első feladat. Legyen adva a térben egy hegyesszögű háromszög. Tekintsük mindazokat a gúlákat, amelyeknek az alapja ez a háromszög, és amelyeknek az oldallapjai is hegyesszögű háromszögek. Mi a mértani helye az alaplappal szemközti (változó) csúcspontból az alaplap síkjára bocsátott merőleges talppontjának?

 
Megoldás: Az ABCΔ síkjának P pontjában a síkra merőleges egyenest állítunk, és ezen az egyenesen egy D pontot veszünk fel. Vizsgáljuk, mitől függ az, hogy D megválasztható-e a feladat kívánalmának megfelelően, úgy tehát, hogy az ABD, BCD, CAD háromszögek mindegyike hegyesszögű legyen.
Először e háromszögeknek az ABCΔ oldalain nyugvó szögeit tekintjük, és közülük pl. a BAD∢-et vizsgáljuk. E szög akkor és csak akkor hegyes, ha D az A-ban AB-re merőlegesen emelt síknak ugyanazon az oldalán van, mint a B pont. Ez a kikötés a P-ben emelt merőlegesnek vagy minden pontjára teljesül, vagy egyikre sem, hiszen ez az egyenes párhuzamos a mondott síkkal. Így tehát csak P megválasztásától függ az, hogy a most vizsgált hat szög hegyes-e. Ez akkor és csak akkor következik be a P-ben emelt merőleges minden D pontjára, ha magára P-re is teljesül, ha tehát a
BAP∢,ABP∢,CBP∢,BCP∢,ACP∢,CAP∢
mindegyike hegyes szög.
Most az ABD, BCD, CAD háromszögek D csúcsú szögeit vizsgáljuk. Tudjuk, hogy a síkban egy pontból egy szakasz akkor látható hegyes szögben, ha a pont a szakasz Thales-körén kívül van. A három vizsgált szög tehát akkor hegyes szög, ha D messzebb van az ABCΔ három oldalának felezőpontjától, mint e három oldal hosszának fele. Ilyen D pont mindig van a P-ben emelt merőleges egyenesen, bárhogyan választjuk is meg a P pontot, hiszen elég pl. azt megkövetelni, hogy D messzebb legyen az ABC síktól, mint az ABCΔ oldalai leghosszabbikának a fele.
Az elmondottakból következik, hogy a feladat kérdésére felelünk, ha azoknak a P pontoknak a mértani helyét állapítjuk meg, amelyekre a fentebb felsorolt hat szög mindegyike hegyes.
A BAP∢ és ABP∢ mindegyike akkor és csak akkor hegyes, ha P annak a síksávnak belsejében van, amelyet az A, B pontokban AB-re emelt merőlegesek határolnak. Ez abból következik, hogy pl. a BAP∢ akkor hegyes, ha P az A-ban emelt merőlegesnek ugyanazon az oldalán van, mint a B pont. A keresett mértani hely ezek szerint három síksáv belsejének közös részeként adódik, s e síksávokat az ABCΔ oldalaira végpontjaikban emelt merőlegesek határolják.
Ha hegyesszögű ABCΔ-ből indulunk ki, akkor a három sáv közös részeként hatszög adódik (lásd 1. ábra), s a keresett mértani hely e hatszög belseje.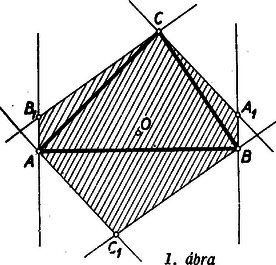
 
 


Megjegyzések. 1. Ha az ABCΔ nem hegyesszögű, akkor a szerepeltetett síksávok közös része nem hatszög, hanem parallelogramma, és e parallelogramma belseje adja a vizsgált mértani helyet. A 2. ábra derékszögű és tompaszögű háromszög esetében mutatja be ezt a mértani helyet.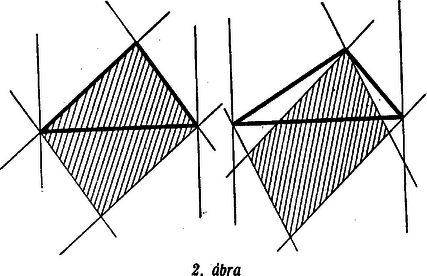
 
 

2. Hegyesszögű háromszög esetében akkor is beláthatjuk, hogy mértani helyként valóban hatszög adódik, ha az ábra szemléletére nem támaszkodunk.
Evégből először azt állapítjuk meg, hogy a szereplő síksávok mindegyike szimmetrikus a háromszög köré írt kör O középpontjára vonatkozólag, hiszen ez a pont a sávok középvonalain, az oldalak felező merőlegesein helyezkedik el. Ebből következik, hogy a három sáv közös része is szimmetrikus ugyanerre a pontra vonatkozólag.
A BC és CA szélességű sávok közös része egy C csúcsú parallelogramma, hiszen ez a két sáv nem párhuzamos egymással. Minthogy az ABCΔ hegyesszögű, C a harmadik, AB szélességű sáv belsejében van, és ezért C a három sáv közös részének is csúcsa. Hasonló indokolással ugyanezt az A és B pontokról is elmondhatjuk.
Az O-ra vonatkozó centrális szimmetriából következik tehát, hogy az A, B, C pontoknak O-ra vonatkozó tükörképei, az A1, B1, C1 pontok, ugyancsak szerepelnek a közös rész csúcsai között. Az A, B, C, A1, B1, C1 pontok mind különbözők, mert O nem azonos az ABCΔ oldalai egyikének felezőpontjával, valamint egyik csúcsával sem. Több csúcsa a közös részként adódó sokszögnek nem lehet, mert a három sávnak együttesen hat határegyenese van, és ezért a közös résznek hatnál több oldala nem lehet. A közös rész ezek szerint valóban hatszög.
3. Az A1, B1, C1 pontokhoz nemcsak úgy juthatunk el, hogy az A, B, C pontokat az O pontra vonatkozólag tükrözzük, hanem úgy is, hogy az ABCΔ M magasságpontját tükrözzük az oldalak felezőpontjaira vonatkozólag. (3. ábra)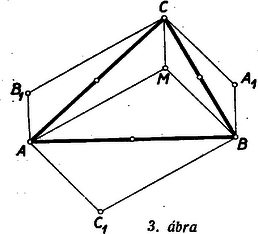
 
 

Ez abból következik, hogy ha M jelöli a C1 pontnak az AB oldal felezőpontjára vonatkozó tükörképét, akkor AC1BM parallelogramma. Ezért AM és BM is merőlegesek a BC, ill. AC oldalakra, M tehát két magasságvonal metszéspontja, azaz a magasságponttal azonos.
A most belátott tényből következik, hogy hatszögünk területe az ABCΔ területének kétszerese, hiszen e háromszögön túlnyúló részei egybevágók az AMB, BMC, CMA háromszögekkel, és ezek együttesen az ABCΔ-et alkotják.
4. A feladat megoldása módot nyújt 4 olyan pont meghatározására, amelyek közül akárhogyan választunk is ki hármat, mindig egy hegyesszögű háromszög három csúcsához jutunk. Megemlítjük, hogy senkinek sem sikerült eddig feleletet adni arra a kérdésre, vajon 4 helyett legfeljebb hány ilyen tulajdonságú pontot lehet megadni.
 
Második feladat. Egy gyár hat különböző színű fonalból kétszínű kelméket gyárt. Minden szín legalább háromféle párosításban szerepel. Bizonyítandó, hogy kiválasztható háromféle kelme úgy, hogy mindegyik szín előforduljon valamelyiken.
 
I. megoldás. Jelöljük 1, 2, 3, 4, 5, 6 számokkal a szereplő színeket és számpárokkal az ezekkel a színekkel gyártható kelméket. Induljunk ki egy gyártott kelméből, pl. az 56 kelméből. Ha az 12 és 34, valamint az 13 és 24 kelmepárok valamelyike két gyártott kelméből áll, akkor már eljutottunk három kívánt tulajdonságú kelméhez. Ha ez nincs így, akkor mind a két kelmepárban van nem gyártott kelme, pl. az 12 és 13 kelméket nem gyártják. Nem jelent megszorítást, hogy csak ezt az esetet vizsgáljuk, mert átszámozással mindig elérhetjük minden még el nem intézett helyzetnél, hogy ez az eset álljon elő.
Mivel minden szín legalább háromféle párosításban szerepel a gyártott kelmék között, minden szín csak legfeljebb kétféleképpen párosítható más színnel úgy, hogy nem gyártott kelme színpárjához jussunk. Ezért tudjuk, hogy 14 gyártott kelme, hiszen az 12 és 13 kelméket nem gyártják. Feltehetjük, hogy 23 nem gyártott kelme, mert különben 14, 23, 56 célunknak megfelelő kelmekiválasztás volna.
Ha viszont 12 és 23 nem gyártott kelmék, akkor az előbb mondottak szerint következik, hogy 25-nek gyártott kelmének kell lennie. Abból, hogy 13 és 23 nem gyártott kelmék, ugyanúgy következik, hogy a 36 kelmét gyártják. Ilyen módon a feladat kívánalmának megfelelő 14, 25, 36 kelmekiválasztáshoz jutottunk.
 
Megjegyzés. Megtehetjük, hogy a színeket pontokkal ábrázoljuk és azokat a pontpárokat, amelyek gyártott kelme színpárját adják, egy élnek mondott vonallal kötjük össze. A gyártott kelmék így egy ábrát, gráfot szolgáltatnak. Ennek a gráfnak hat szögpontja van, két-két szögpontját legfeljebb egy él köti össze, és a feladat kikötése szerint minden szögpontból legalább három él indul ki. A feladat annak bizonyítását kívánja, hogy a gráf élei közül kiválasztható három úgy, hogy végpontjaik mind különbözők legyenek.
Azt, hogy két szögpontot nem köt össze él, jelölhetjük azzal, hogy ezt a két szögpontot szaggatott vonallal kötjük össze. Ilyen megállapodás mellett készült a közölt első megoldás okoskodását szemléltető 4. ábra.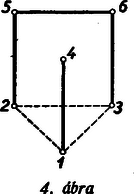
 
 

Ebben csak azokat az éleket és élhiányokat tüntettük föl, amelyek a megoldásban szóhoz jutottak.
 

II. megoldás. Ismét számokkal jelöljük a színeket és számpárokkal a kelméket. Feltehetjük, hogy az 12 kelmét gyártják. Mivel a 3 szín legalább háromféle párosításban szerepel a gyártott kelmék között, szerepelnie kell az 1, 2 színektől különböző színnel párosítva. Feltehetjük ezért, hogy 34 is gyártott kelme, s hogy az 56 kelmét nem gyártják, mert különben máris eljutottunk volna egy, a követelményt kielégítő kelmekiválasztáshoz. (Okoskodásunkat a 4. ábra módszerévél az 5. ábra szemlélteti.)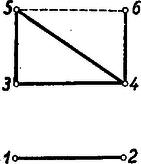
 
 
5. ábra
 

Mivel az 56 kelmét nem gyártják, s az 5 szín legalább három színnel párosítva gyártásra kerül, az 15, 25, 35, 45 kelmék közül legalább hármat gyártanak, azaz legfeljebb egyet nem gyártanak. Feltehetjük tehát, hogy a 35 és 45 kelmék mindegyikét gyártják, mert különben átszámozással érhetnők el ezt a helyzetet.
Miként az 5 szín esetében tettük, a 6 színről is beláthatjuk, hogy az 16, 26, 36, 46 kelmék közül legfeljebb egyet nem gyártanak. Gyártják ezért a 36, 46 kelméknek legalább az egyikét. Ha pl. 46 gyártott kelmét jelöl, akkor az 12, 35, 46 kelmekiválasztás kielégíti a feladat követelményét.
 
Megjegyzések. 1. Helyes a feladat állításának következő általánosítása: Egy gyár legalább hat különböző színű fonalból kétszínű kelméket gyárt. Minden szín legalább háromféle párosításban szerepel. Kiválasztható akkor háromféle kelme úgy, hogy ezeken hat különböző szín szerepeljen. Ennek az állításnak a bizonyítását megkapjuk, ha a közölt második megoldásban ,,az 56 kelmét nem gyártják'' szavakat az ,,és az 5, 6 színeket magasabb sorszámú színnel sem párosítják'' szavakkal toldjuk meg.
2. A feladat állításának másirányú általánosítása a következő: Egy gyár 2n különböző fonalból kétszínű kelméket gyárt. Minden szín legalább n-féle párosításban szerepel. Kiválasztható akkor n-féle kelme úgy, hogy mindegyik szín előforduljon valamelyiken. Itt n tetszőleges természetes számot jelöl. A második megoldás gondolatmenetével ezt az általánosítást is bizonyíthatjuk.
Válasszuk ki a lehető legtöbb kelmét úgy, hogy a kiválasztott kelméken csupa különböző szín szerepeljen. Tegyük fel, hogy k darab kelmét választhatunk így ki, s hogy k<n. Ha ebből ellentmondásra tudunk következtetni, akkor bebizonyítottuk, hogy k=n, azaz állításunk helyes.
A k darab kiválasztott kelme színeit 1, 2,...,2k számokkal jelöljük. Mivel k<n, vannak 2k-nál nagyobb sorszámú színek is. Bizonyos, hogy a 2n-1 és 2n színek az utóbb említett színek közül valók.
Bármely két 2k-nál nagyobb sorszámú színről megállapíthatjuk, hogy ilyen színösszeállítású kelme nem készül, hiszen különben a k darab kelme kiválasztását ennek a kelmének kiválasztásával folytathattuk volna. Igaz ezért, hogy a 2n-1 és 2n színek csak az 1, 2,...,2k színek között előfordulókkal lehetnek párosítva, s így közülük legalább n-féle színnel valóban párosítva is vannak.
Az 1, 2,...,2k színeket a k darab kiválasztott kelme párokba sorolja.Tekintsük e 2k-féle szín közül azt a legalább n-et, amelyeknek párjai a 2n-1 színnel párosítva gyártásra kerültek. Ha ezt a legalább n-féle színt az 1,2,...,2k színek közül elhagyjuk, akkor legfeljebb 2k-n, tehát n-nél kevesebb szín marad. Ebből az következik, hogy a tekintett legalább n-féle szín között kell lennie a 2n színnel párosítottnak, hiszen a 2n szín is legalább n színnel van párosítva az első 2k szín közül.
Beláttuk így, hogy a kiválasztott k darab kelme között van olyan, amelyiknek egyik színe a 2n-1 színnel, másik színe a 2n színnel is párosítva van. Hagyjuk el ezt a kelmét a kiválasztott k darab kelme közül, s a maradó k-1 darab kelméhez csatoljuk hozzá azt a két kelmét, amelyeken az elhagyott kelme színei, valamint a 2n-1, 2n színek szerepelnek. Ilyen módon k+1 csupa különböző színt tartalmazó kelméhez jutottunk. Ez ellentmond annak, hogy k értékét a lehető legnagyobbnak választottuk, s ez az ellentmondás állításunk helyességét bizonyítja.
3. A most bizonyított általánosítást tovább általánosíthatjuk ugyanúgy, ahogyan a feladat állítását először általánosítottuk. Így a következő általánosításhoz jutunk: Egy gyár legalább 2n különböző fonalból kétszínű kelméket gyárt. Minden szín legalább n-féle párosításban szerepel. Kiválasztható akkor n-féle kelme úgy, hogy ezeken 2n különböző szín szerepeljen. Ez az általánosítás magában foglalja az előző kettőnek mindegyikét. Bizonyítása új okoskodást nem kíván, mert a második általánosítás bizonyítása szószerint alkalmazható ennek bizonyítására is.
4. Felmerülhet a kérdés, nem lehet-e olyan irányban tovább általánosítani eddigi eredményeinket, hogy minden szín esetében n-nél kevesebb párosításban való gyártást követelünk meg. Vonatkozik ez a kérdés az n=3 esetre is.
Akkor sem jutunk helyes kijelentéshez, ha n-et minimálisan, ti. (n-1)-re csökkentjük. Ezt a következő példával bizonyítjuk: Legyen 2n a színek száma, és osszuk ezeket egy n-1 színből és egy n+1 színből álló csoportra. Gyártsuk mindazokat a kelméket, amelyeken egy első csoportba tartozó és egy második csoportba tartozó szín szerepel.
Most minden szín legalább n-1 párosításban szerepel, viszont n kelme a színek mindegyikét nem tartalmazhatja, hiszen a második csoportot alkotó n+1 szín közül csak legfeljebb n szín szerepelhet a kiválasztott n-féle kelmén.
 
III. megoldás. Képzeljük úgy, hogy mindenféle színpárosítással gyártanak kelmét, de nem mindegyiket hozzák forgalomba. Feladatunk ekkor a forgalomba hozott kelmékről szól. Mi most a raktáron maradó kelméket fogjuk vizsgálni.
Ha találunk a forgalomba hozott kelmék között olyat, amelyiknek a forgalomból való kivonása után a feladat kikötése továbbra is teljesül (hogy ti. minden szín legalább háromféle párosításban szerepeljen), akkor ezt a kelmét vonjuk ki a forgalomból. Folytassuk a raktárnak ezt a szaporítását mindaddig, amíg el nem mondhatjuk, hogy bármelyik további kelmének a forgalomból való kivonása után már lenne olyan szín, amelyik csak kétféle párosításban szerepelne a forgalomban maradó kelmék között. Elég, ha a feladat állítását az ilyen helyzetekre bizonyítjuk, mert az ilyen helyzetben lehetséges kelmekiválasztás a forgalomból kivont kelmék újbóli piacradobása után is lehetséges marad.
A raktár kelméin belül minden szín csak legfeljebb kétféle párosításban szerepelhet, hiszen legalább háromféle párosítása forgalomban van. Előző megállapításunk értelmében azt is kimondhatjuk, hogy a most mondott tulajdonság már nem maradna meg, ha a raktárt bármely további kelmével szaporítanók. Vizsgáljuk meg, hogy ilyen kikötések mellett a raktár milyen kelméket tartalmazhat.
A vizsgálatot megkönnyítjük azzal, hogy a színeket pontokkal ábrázoljuk, és szaggatott vonallal kötjük össze azokat a pontpárokat, amelyek egy a raktáron található kelme színeit adják. Ilyen módon egy gráf szögpontjaihoz és éleihez jutottunk. A gráf egy szögpontját annyiadrendűnek mondjuk, ahány él ebből a szögpontból kiindul. Kikötéseink szerint a gráf minden szögpontja legfeljebb másodrendű, és ez nem maradna igaz, ha a gráfhoz akármilyen további élt csatolnánk.
Ebben a gráfban csak akkor szerepelhet két 2-nél kisebb rendszámú szögpont, ha ezt a két szögpontot él köti össze, hiszen különben ezt az összekötő élt a gráfhoz csatolhatnók, és ezután sem keletkeznék 2-nél nagyobb rendszámú szögpont. Ebből következik, hogy csak a következő esetek lehetségesek: 1) a gráf minden szögpontja másodrendű, 2) csak egyetlen egy szögpont rendszáma kisebb 2-nél, a többi mind másodrendű, 3) két elsőrendű szögpontot él köt össze, a többi szögpont másodrendű. Ha ugyanis volna három 2-nél kisebb rendszámú szögpont, akkor ezeknek páronként éllel kellene összekötve lenniök, és így mégis csak kiindulna két-két él ebből a három szögpontból.
Minden él két szögpontba fut, ezért valamennyi él valamennyi végét összeszámlálva páros számot kell kapnunk. Ez azt jelenti, hogy a gráf valamennyi szögpontjának rendszámát összeadva páros számot kell kapnunk. Ebből következik, hogy ha csak egy szögpont rendszáma kisebb 2-nél, akkor ebből a szögpontból nem indul ki egyetlen él sem. Így azt is beláttuk, hogy ha a raktárt ábrázoló gráfnak egy éle másodrendű szögpontból indul ki, akkor ennek az élnek a másik végpontja is másodrendű szögpont.
A másodrendű szögpontokat összekötő élekről megállapíthatjuk most már, hogy ezek szögpontokban egymáshoz csatlakozó élekből álló körutakat, ,,sokszögeket" alkotnak, hiszen bármelyikből bármilyen irányban elindulhatunk, s a végpontok másodrendűsége miatt az utat mindaddig folytathatjuk, amíg már bejárt élre nem lépünk. Ilyenkor csak a kezdőél kezdőpontjához juthattunk, mert a bejárt élek többi végpontjaiba csak már bejárt élek futnak. Már láttuk, hogy gráfunknak hat, öt vagy négy másodrendű szögpontja van. Az ezekből kiinduló élek az első esetben vagy hatszöget, vagy két háromszöget, a második és harmadik esetben pedig csak ötszöget, ill. négyszöget alkothatnak, hiszen minden sokszögnek legalább három oldala van.
Megállapításainkat összefoglalva kimondhatjuk, hogy a forgalomba nem hozott kelmék raktárát ábrázoló gráf csak a következők valamelyike lehet: 1a) hatszög, 1b) két közös szögpont nélküli háromszög, 2) ötszög és egy további szögpont, amelyből nem indul ki él, 3) négyszög és két további, éllel összekötött szögpont. Ezeket az eseteket a 6. ábra mutatja be.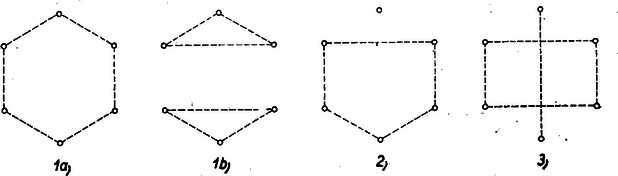
 
 
6. ábra
 

Könnyű most már mind a négy esetben három további élt úgy berajzolni, hogy ennek a három élnek mind a hat szögpontja más-más szögpont legyen. A 7. ábrán két ilyen élhármast láthatunk, amelyeknek mindegyike megfelel a 6. ábrának mind a négy gráfjánál. Ez azt jelenti, hogy a forgalomba hozott kelmék közül mindig kétféleképpen is kiválaszthatunk hármat a feladat követelményének megfelelő módon.
 

Megjegyzések. 1. Megoldásunkból a feladat állításának újabb általánosítását olvashatjuk ki. Hogy ezt könnyebben megtehessük, előbb átfogalmazzuk az eredeti feladatot. Nem szorul magyarázatra, hogy feladatunk állítása a következő kijelentéssel egyenértékű: Egy társaságnak hat tagja van. A hat személy mindegyikének legalább három ismerőse van a társaság tagjai között. Le lehet akkor ültetni a társaság tagjait három asztalhoz úgy, hogy mindegyik asztalnál ketten, éspedig ismerősök üljenek.
Ha a 7. ábra két rajzát egymásra fektetjük, akkor a 8. ábra hatszögéhez jutunk. Mivel beláttuk, hogy található ilyen hatszög, bebizonyítottuk a feladat állításának következő általánosítását: Egy társaságnak hat tagja van. A hat személy mindegyikének legalább három ismerőse van a társaság tagjai között. Le lehet akkor ültetni a társaság tagjait egy kerek asztalhoz úgy, hogy mindenki mindkét oldalról ismerős mellett üljön.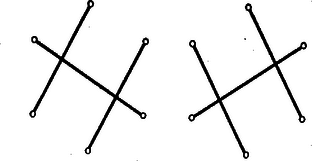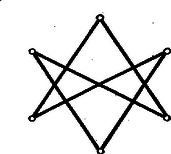
 
 
7. ábra
 
 
 
8. ábra
 

Eredményünket a gráfok körén belül maradva is megszövegezhetjük. Ha egy gráf éleiből olyan körutat lehet alakítani, amelyik szögpontokban egymáshoz csatlakozó élekből áll, s amelyik minden szögponton áthalad, és csak egyszer halad át, akkor ezt a gráf Hamilton-féle körútjának nevezzük, magát a gráfot pedig Hamilton-félének mondjuk. Eredményünk ezek után így szövegezhető: Ha egy grófnak hat szögpontja van, és ezek mindegyike legalább harmadrendű, akkor ez a gráf Hamilton-féle. Természetesen csak olyan gráfokra gondolunk, amelyekben két szögpontot nem köt össze több él.
2. Eredményünket tovább általánosíthatjuk. Helyesek maradnak kijelentéseink, ha hat és három helyett 2n és n szerepel, és itt n tetszőleges, de 1-nél nagyobb természetes számot jelöl. Ha tehát gráfokról szólunk, akkor a következőt állítjuk: Ha egy gráfnak 2n szögpontja van és n>1, ha továbbá minden szögpont legalább n-edrendű, akkor a gráf Hamilton-féle.
Ennél többet fogunk bizonyítani. Bizonyítjuk, hogy ha egy gráfnak legfeljebb 2n szögpontja van és n>1, ha továbbá minden szögpont legalább n-edrendű, akkor a gráf Hamilton-féle. Könnyű belátni, hogy ez a kijelentés csak a 2n-1 szögpontú gráfokra mond ki olyat, ami nem következik nyomban az előző kijelentésből. A kimondott tételt Dirac Gábor bizonyította 1951-ben. Mi itt csekély módosítással az ő bizonyítását ismertetjük.
Először azt igazoljuk, hogy ha egy gráf kielégíti a tétel követelményeit, akkor alakítható a gráf éleiből olyan körút, amelyik n-nél több élt tartalmaz. Ha körutat mondunk, eleve feltesszük, hogy azt szögpontokban csatlakozó élek alkotják, s hogy a körút egy szögponton sem halad át többször. Állításunk bizonyítása végett induljunk el valamelyik élen egy szögpontból, és az él végpontjában lépjünk rá egy másik élre. Ezt megtehetjük, mert a szögpontok legalább másodrendűek. Folytassuk utunkat egymáshoz szögpontokban csatlakozó éleken át haladva mindaddig, amíg ezt megtehetjük anélkül, hogy már érintett szögpontba jutnánk. Utunk P végpontjára igaz akkor az, hogy az innen tovább vezető élek mindegyikének végpontját érintettük már. E végpontok között van egy, amelyet legkorábban érintettünk. Ha az ebbe vezető élen folytatjuk utunkat, akkor körutat tettünk meg. Ez a körút n-nél több élből áll, mert tartalmazza a P szögpontot és az ebből induló legalább n él végpontjának mindegyikét.
Tételünket indirekt úton bizonyítjuk. Feltesszük, hogy a G gráf kielégíti tételünk követelményeit, de nincs Hamilton-féle körútja. Ebből a feltevésből ellentmondásra fogunk következtetni.
Válasszunk ki egy G éleiből alakított és lehető legtöbb élt tartalmazó K körutat. E körút éleinek számát k-val jelöljük. Már bizonyítottuk, hogy k>n. Van G-nek olyan szögpontja, amelyet K nem tartalmaz, hiszen feltevésünk szerint K nem lehet Hamilton-féle körút. Az ilyen szögpontok száma n-nél kisebb, mert G-nek legfeljebb 2n, K-nak pedig k>n miatt n-nél több szögpontja van. Ebből következik, hogy az ilyen szögpontokból ki kell indulniok a K körúton végződő éleknek, hiszen G minden szögpontja legalább n-edrendű. Van eszerint a K körúton olyan A szögpont, amelyikből kiindul nem a K körúton végződő él is.
Induljunk el az A szögpontból egy ilyen élen, és szögpontokban csatlakozó éleken át tovább haladva menjünk el mindaddig, amíg ezt megtehetjük anélkül, hogy a K körútra lépnénk, vagy utunk során már érintett szögpontba jutnánk. Utunk végpontját B-vel, az AB út éleinek számát l-lel jelöljük. Ez az A-ból kiinduló út l darab, a K körúthoz nem tartozó szögponthoz vezetett el. Ebből k+l≤2n következik, hiszen G-nek legfeljebb 2n szögpontja van. A k>n egyenlőtlenség figyelembevételével ilyen módon l<n helyességét is beláttuk.
Vizsgáljuk most, hogy B-ből hová vezetnek élek. Csak a K körút és az AB út szögpontjaihoz vezethetnek, mert különben az AB utat tovább folytathattuk volna. Az AB út szögpontjaiba csak legfeljebb l él indulhat, ezért K-nak A-tól különböző szögpontjaiba B-ből legalább n-l él indul, hiszen B legalább n-edrendű.
Ha a BC él C végpontja K-nak A-tól különböző szögpontja, akkor a K körúton nem vezethet el A-ból C-be (l+1)-nél kevesebb él. Ez abból következik, hogy az ellenkező esetben a K körutat az ABC kerülővel bővíthetnők, és így egy k-nál több élű körúthoz jutnánk, ami ellentmond K megválasztásának.
Beláttuk ilyen módon, hogy a B szögpontból legalább n-l él indul annak a D1D2 ívnek a szögpontjaihoz, amelyet úgy kapunk meg K-ból, hogy az A szögpontból kiindulva mindkét irányban l+1 csatlakozó élt elhagyunk (lásd 9. ábra).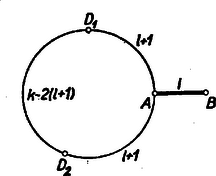
 
 
9. ábra
 

Minthogy n-l pozitív, valóban kell, hogy az elhagyás után még maradjon egy D1D2 ív, de az is lehetséges, hogy ez az ív már csak az egyetlen D1=D2 szögpontból áll. A D1D2 ív éleinek száma az ív származtatása folytán k-2(l+1).
A D1D2 ív két szomszédos szögpontjába nem érkezhetnek élek B-ből, mert akkor a K körutat a B szögponton át vezető kerülővel k+1 élű körúttá bővíthetnők, pedig k-nál többélű körút nincs. A B szögpontból a D1D2 ívhez induló, legalább n-l él végpontjai között az ívnek legalább n-l-1 szakasza helyezkedik el, és beláttuk, hogy ezeknek a szakaszoknak mindegyike legalább két élből áll. Igazoltuk így, hogy a D1D2 ív éleinek száma legalább 2(n-l-1).
A D1D2 ív élszámára vonatkozó eredményeinket egybevetve
k-2(l+1)≥2(n-l-1),
azaz k≥2n adódik. K azonban csak akkor tartalmazhatja G-nek legalább 2n szögpontját, ha G-nek 2n szögpontja van, hiszen több szögpontja nem lehet, s ha a K körút G valamennyi szögpontját tartalmazza. Ez azt jelenti, hogy K Hamilton-féle körút, pedig feltettük, hogy G-nek nincs Hamilton-féle körútja. Ez az ellentmondás tételünk helyességét bizonyítja.
Megemlítjük még, hogy a most bizonyított tételt így is szövegezhetjük: Ha egy gráfnak legalább három szögpontja van, és egy szögpont rendszáma sem kisebb a szögpontszám felénél, akkor a gráf Hamilton-féle.
 
Harmadik feladat. Jelentse a1, a2,...,an az 1, 2,...,n természetes számokat valamilyen sorrendben elrendezve. Határozzuk meg az
|a1-1|+|a2-2|+...+|an-n|
összeg legnagyobb értékét, ha az összes lehetséges elrendezéseket tekintjük.
 

Megoldás. A vizsgált összegben az abszolút érték jeleit elhagyhatjuk, ha ott, ahol negatív szám abszolút értéke szerepelt, a két tag előjelét megváltoztatjuk. Ilyen módon egy 2n tagú összeghez jutunk, amelynek különféle előjelű tagjai között az 1, 2,...,n számok mindegyike kétszer szerepel, és a 2n tag között n negatív előjelű van. A vizsgált érték eszerint az 1, 1, 2, 2, n, n számok összegéből úgy keletkezik, hogy értékét a negatív előjellel fellépő számok összegének kétszeresével csökkentjük. Akkor lesz tehát a kapott érték maximális, ha a negatív előjellel szereplő számok összege minimális. Ez utóbbi összegben n tag van, és értéke nyilván nem lehet kisebb, mint az 1, 1, 2, 2,...,n, n sorozat első n elemének összege.
Ha megfelelő számsorrendből indulunk ki, akkor be is következik az, hogy éppen a mondott első n elem lép fel negatív előjellel. Ezt az n, n-1,...,1 sorrend példája mutatja, amint ezt az adódó
|n-1|+|(n-1)-2|+...+|1-n|
összegből nyomban kiolvashatjuk.
Feladatunk most már csak az, hogy ezt az összeget kiszámítsuk. Ennek az összegnek a tagjai, akár balról, akár jobbról vesszük sorra azokat, (n-1)-től 2 különbséggel csökkenő számtani haladványt alkotnak. E haladványok tagjai addig csökkennek, amíg csak az összeg közepéig el nem jutunk. Itt vagy két 1 értékű tagot, vagy pedig egy 0 értékűt találunk.
Ha tehát n páros, akkor a vizsgált összeg az 1-től (n-1)-ig terjedő, 2 különbségű és n2 tagszámú számtani haladvány összegének kétszerese, azaz n22. Ha viszont n páratlan, akkor a 2-től (n-1)-ig terjedő, 2 különbségű és n-12 tagszámú számtani haladvány összegének kétszerese, azaz n-12(n+1)=n2-12 adódik.
Az eredményt mind a két esetben [n22] alakban írhatjuk, ha a szögletes zárójellel a számban foglalt egész számok legnagyobbikát jelöljük.
 
Megjegyzés. Számtani haladvány összegezése nélkül is célt érhetünk, ha ügyesen megválasztott számsorrendből indulunk ki.
Ha n=2k, akkor a k+1, k+2,...,2k, 1, 2,...,k sorrendből indulhatunk ki. A fellépő különbségek kisebb tagjai itt az 1, 2,...,k számok, és mindegyikük kétszer lép fel. Megoldásunk gondolatmenete alapján kimondhatjuk tehát, hogy a választott számsorrend a maximális összeghez vezet. A különbségek mindegyikének k az abszolút értéke, s ezért az abszolút értékek összege 2k2.
Ha viszont n=2k+1, akkor a k+2, k+3,...,2k+1, k+1, 1, 2,...,k sorrend vezet célhoz. A fellépő különbségek kisebb tagjaiként ismét ugyanazokat a számokat kapjuk, mint az előbb, de a középső különbségben a kisebbítendő és a kivonandó egyaránt k+1. Ebből megint ugyanúgy következik, hogy a maximális összeghez jutunk. Most a középső különbség 0, a többinek pedig k+1 az abszolút értéke. Ilyen módon a 2k(k+1) összeg adódik.
Megállapíthatjuk, hogy az eredmény mind a két esetben az n22-ben foglalt legnagyobb egész szám.