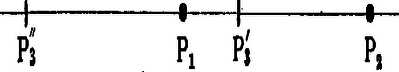Kezdőlap


Cím:	Bizonyos típusú szélsőértékfeladatokról (2. befejező közlemény)
Szerző(k):	Turán Pál
Füzet:	1958/április, 97 - 101. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A cikkünk első részében felvetett feladat teljes megoldásához a következő kérdések tisztázandók.
a) ,,Jó'' háromszögben van-e mindig (5) tulajdonságú pont?
b) Ha van, lehet-e több?
c) Az (5) tulajdonság fennállása egy belső $P$ pontra vajon elégséges is-e ahhoz ,,jó'' háromszög esetén, hogy $P$ minimizáló pont legyen? d) Az (5) tulajdonságú pont, ha van, hogyan szerkeszthető?
e) ,,Rossz'' háromszög esetén lehet-e több (8) tulajdonságú pont?
f) A (8) tulajdonság $P$ -re fennállása ,,rossz'' háromszög esetén elégséges-e ahhoz, hogy $P$ minimalizáló pont legyen?
d) Kérdésre a válasz igen könnyű. Nyilván

\begin{matrix} \frac{\bar{P P_{1}}}{\bar{P P_{2}}} = \frac{p_{1}}{p_{2}}, \end{matrix}

(12)

azaz

P

P_{1}

és

P_{2}

pontokhoz, valamint a

\frac{p_{1}}{p_{2}}

arányhoz tartozó Apollonius-körön fekszik, amely ismert módon szerkeszthető. Mivel

\begin{matrix} \frac{\bar{P P_{2}}}{\bar{P P_{3}}} = \frac{p_{2}}{p_{3}}, \end{matrix}

tehát

P

P_{2}

és

P_{3}

pontokhoz, valamint a

\frac{p_{2}}{p_{3}}

arányhoz tartozó Apollonius-körön is fekszik, azaz

P

, mint ezek metszéspontja, meg van szerkesztve. A b) kérdésre vonatkozólag a felelet az, hogy minden háromszögben legfeljebb egy (5) tulajdonságú

P

pont van. Ennek igazolására legyen először

p_{1} < p_{2} < p_{3}

. Ekkor azt állítjuk, hogy a (12) tulajdonságú

P

pontokból álló kör középpontja a

P_{1} P_{2}

oldalon, de

P_{1} P_{2}

szakaszon kívül van. Ugyanis, ha a

P_{1} P_{2}

szakaszon levő

P_{3}'

pontra

\frac{\bar{P_{1} P_{3}'}}{\bar{P_{3}' P_{2}}} = \frac{p_{1}}{p_{2}}

, akkor

P_{1} P_{3}' = \frac{p_{1}}{p_{1} + p_{2}} \bar{P_{1} P_{2}}

, továbbá, ha a

P_{1}

-től

P_{2}

-vel ellentétes oldalra eső

P_{3}''

pontra

\frac{\bar{P_{1} P_{3}''}}{\bar{P_{3}'' P_{2}}} = \frac{p_{1}}{p_{2}}

, akkor

\begin{matrix} \bar{P_{3}'' P_{1}} = \frac{p_{1}}{p_{2} - p_{1}} P_{1} P_{2}, \end{matrix}

azaz

\bar{P_{3}'' P_{1}} > \bar{P_{3}' P_{1}}

, a kérdéses kör középpontja pedig

\bar{P_{3}' P_{3}''}

felezőpontja.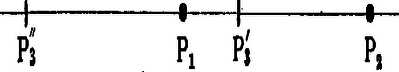

3. ábra

Tehát mindhárom Apollonius-kör középpontja a háromszög egy-egy oldalán van, de mind a meghosszabbításokon. Ha mármost a háromszögben legalább két pont volna (5) tulajdonsággal, akkor a két pont felezőmerőlegesén az Apollonius-körök középpontjai szintén rajta volnának, ami pedig legalább két oldalt belül metsz, ez viszont ellentmondás. Ha

p_{1} < p_{2} < p_{3}

helyett

p_{1} ≦ p_{2} ≦ p_{3}

áll, a bizonyítás lényegtelenül módosul.
Tekintsük a legkényesebb c) kérdést. Amit mi csináltunk, az az, hogy megmutattuk, hogy ,,jó''

{P_{1} P_{2} P_{3}}_{▵}

esetén a sík egyetlen olyan

P

pontja sem lehet minimizáló pont, amely nem elégíti ki (5)-öt, mert

\begin{matrix} max (\frac{1}{p_{1}} \bar{P P_{1}}, \frac{1}{p_{2}} \bar{P P_{2}}, \frac{1}{p_{3}} \bar{P P_{3}}) \end{matrix}

csökkenthető és ezen eljárás csak az (5) tulajdonságú

P

-re (amennyiben ilyen létezik) nem vezet csökkentéshez. Ebből

100

évvel ezelőtt még olyan matematikus is, mint Jacob Steiner, a pásztorfiúból lett híres geométer, arra következtetett volna, hogy (5) tulajdonságú

P

pont létezik és minimizál. Ez valóban korrekt volna, ha biztos volna, hogy a maximumot minimizáló keresett

P

pont és a maximum minimuma tényleg léteznek. Jólismert példa azonban az itt fellépő tényállásra azon kérdés, melyik a legnagyobb pozitív egész. Ezen maximum nyilván nem létezik. Viszont minden egészhez a négyzetét hozzárendelve adódik egyfelől, hogy semmilyen

1

-nél nagyobb pozitív egész nem lehet maximum, mert a hozzárendelt érték egy nagyobb pozitív egész. Másfelől ezen eljárás az

1

-hez önmagát rendeli hozzá, ami nála nem nagyobb; ha tehát Steiner következtetési módja helyes volna, ez azt adná, hogy

1

a legnagyobb pozitiv egész, ami nem áll. Viszont Weierstrass alapvető vizsgálatai a szélsőértékfeladatok egy igen tág osztályára, amelybe a miénk is tartozik, a minimum létezését eleve biztosítják; ebből következik tehát az a) és c) kérdésekre adódó feleletként, hogy ,,jó'' háromszögben mindig van (5) tulajdonságú pont és ez tényleg minimizáló pont.
Az e) kérdésre a (11) alatti gondolat segítségével adhatunk nemleges választ. Ha ugyanis a (8) tulajdonság a

P_{1} P_{2}

oldalon teljesülne egy

P = P_{3}'

pontra és

P_{2} P_{3}

-on egy

P = P_{1}'

pontra, akkor (11)-et előbb

P_{1} P_{2}

-re alkalmazva

Q = P_{1}'

-vel, adódik

\begin{matrix} {max}_{}^{} (\frac{1}{p_{1}} \bar{P_{1} P_{3}'}, \frac{1}{p_{2}} \bar{P_{2} P_{3}'}, \frac{1}{p_{3}} \bar{P_{3} P_{3}'}) < {max}_{}^{} (\frac{1}{p_{1}} \bar{P_{1}' P_{1}}, \frac{1}{p_{2}} \bar{P_{1}' P_{2}}, \frac{1}{p_{3}} \bar{P_{1}' P_{3}}), \end{matrix}

azután (11)-et

P_{2} P_{3}

-ra alkalmazva

Q = P_{3}'

-vel

\begin{matrix} {max}_{}^{} (\frac{1}{p_{1}} \bar{P_{1} P_{1}'}, \frac{1}{p_{2}} \bar{P_{2} P_{1}'}, \frac{1}{p_{3}} \bar{P_{3} P_{1}'}) < {max}_{}^{} (\frac{1}{p_{1}} \bar{P_{1} P_{3}'}, \frac{1}{p_{2}} \bar{P_{2} P_{3}'}, \frac{1}{p_{3}} \bar{P_{3} P_{3}'}), \end{matrix}

de ez a két egyenlőtlenség egymásnak ellentmond.
Tehát ,,rossz'' háromszög esetén csak az egyetlen (8) tulajdonságú pont lehet a minimizáló. Mivel Weierstrass előbb említett általános tétele szerint minimizáló pont van, tehát a minimizáló pont ez esetben tényleg a (8) alatti pont, igenlő választ adva az f) kérdésre.
Összefoglalva a feladat megoldása a következő.
Ha a háromszög (9)‐(10) értelemben ,,jó'', akkor a háromszögben egyetlen

P

pont van az (5) tulajdonsággal, és ez a minimizáló pont. Ha a háromszög nem ,,jó'', akkor egyetlen pont van a háromszög kerületén, amelyre (8) teljesül, és ez a minimizáló pont.
Hogy a ,,rossz'' háromszögek kissé jobban láthatók legyenek, megjegyzem, hogy ezek a következő módon származtathatók. Legyen a látható 4. ábrán

\bar{A D} = p_{1}

\bar{B D} = p_{2}

és

\bar{C D} = p_{3}

, ilyen háromszög végtelen sok van és e háromszögek

C

csúcsai a

D

középpontú és

p_{3}

sugarú körön fekszenek.

4. ábra

Ha ezeket mintaháromszögeknek nevezzük, akkor azok a ,,rossz'' háromszögek, amelyek hasonlóak egy olyanhoz, melynek alapja

A B

és benne van egy mintaháromszögben. Belátható volna, hogy a ,,rossz'' háromszögekre is létezik az (5) tulajdonságú pont, csak a háromszögön kívül esik; mivel erre a szélsőértékfeladat szempontjából nincs szükség, ennek bizonyításával nem foglalkozunk.
Mint általában lenni szokott, egy megoldott feladat egy csomó egyéb kérdést is hoz felszínre, melyek érdekessége már elsősorban matematikai természetű és gyakran bizonyos szimmetriaérzék hozza őket létre. Így jelen feladathoz kézenfekvő azt kérdezni, milyen

R

pont esetén lesz

\begin{matrix} {min}_{}^{} (\frac{1}{p_{1}} \bar{R P_{1}}, \frac{1}{p_{2}} \bar{R P_{2}}, \frac{1}{p_{3}} \bar{R P_{3}}) \end{matrix}

(14)

maximális. Könnyű azonban látni, hely ennek a feladatnak nincs megoldása. Ha ugyanis

R

a háromszögtől ,,messze'' van, akkor (14) értéke ,,nagy'', sőt tetszőleges nagy lehet, amint

R

elég messze van. Másik kézenfekvő kérdés a csúcsoktól való helyett az oldalaktól valókat venni és azt kérdezni, hogy adott pozitív

q_{1}

q_{2}

és

q_{3}

mellett mikor lesz

\begin{matrix} {max}_{}^{} (\frac{1}{q_{1}} d_{1} (P), \frac{1}{q_{2}} d_{2} (P), \frac{1}{q_{3}} d_{3} (P)) \end{matrix}

minimális, ahol

d_{1} (P)

d_{2} (P)

d_{3} (P)

egy

P

belső pontnak az oldalaktól való távolságai. Ekkor azt állítjuk, hogy a

P_{1} P_{2} P_{3}

háromszögben van pontosan egy

Q

pont, amelyre

\begin{matrix} \frac{1}{q_{1}} d_{1} (Q) = \frac{1}{q_{2}} d_{2} (Q) = \frac{1}{q_{3}} d_{3} (Q) \end{matrix}

(15)

és ez lesz az egyetlen minimizáló pont. Ennek bizonyítása hasonló az előbbihez, de annál egyszerűbb; a két megoldás hasonlósága mégis alkalmas lesz annak illusztrálására, hogy itt egységes módszerről van szó, szemben a tisztán geometriai módszerek individualitásával.
Hogy (15) tulajdonságú pont a háromszögben van és egyetlen egy van, az rögtön következik onnan, hogy azon

R

pontok mértani helye, melyekre

\begin{matrix} \frac{d_{1} (R)}{d_{2} (R)} = \frac{q_{1}}{q_{2}}, \end{matrix}

nyilván egy

P_{3}

-ból kiinduló egyenes. Így a (15) alatti

Q

pont, mint a

\begin{matrix} \frac{d_{1} (R)}{d_{2} (R)} = \frac{q_{1}}{q_{2}} és \frac{d_{1} (R)}{d_{3} (R)} = \frac{q_{1}}{q_{3}} \end{matrix}

egyenesek metszéspontja adódik; ezen a

\begin{matrix} \frac{d_{2} (R)}{d_{3} (R)} = \frac{q_{2}}{q_{3}} \end{matrix}

egyenes nyilvánvalóan áthalad.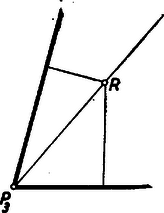

5. ábra

Hogy minimizáló pont létezik, az ismét Weierstrass általános tételéből következik. Elég tehát igazolni, hogy ha

R

különbözik a (15) alatti

Q

-tól, akkor

R

nem lehet minimizáló pont. Tegyük fel először, hogy

\begin{matrix} \frac{d_{1} (R)}{q_{1}} ≦ \frac{d_{2} (R)}{q_{2}} < \frac{d_{3} (R)}{q_{3}} . \end{matrix}

(16)

Ekkor

R

-et ,,kissé'' közelítve a

P_{1} P_{2}

oldalhoz,

\frac{1}{q_{3}} d_{3} (R)

fogy; ha a közelítés elég kicsi, akkor

\frac{1}{q_{1}} d_{1} (R)

és

\frac{1}{q_{2}} d_{2} (R)

esetleg nőnek, de mégsem annyit, hogy ,,elérjék''

\frac{1}{q_{3}} d_{3} (R)

-et, azaz az elmozdítás következtében

\begin{matrix} {max}_{}^{} (\frac{1}{q_{1}} d_{1} (R), \frac{1}{q_{2}} d_{2} (R), \frac{1}{q_{3}} d_{3} (R)) \end{matrix}

fogy. Ha

\begin{matrix} \frac{1}{q_{1}} d_{1} (R) < \frac{1}{q_{2}} d_{2} (R) = \frac{1}{q_{3}} d_{3} (R), \end{matrix}

(17)

akkor

R

-et a

P_{1} R

egyenes mentén

P_{1}

-hez közelítve ,,egy kissé''

d_{2} (R)

és

d_{3} (R)

mindkettője fogy, de még úgy, hogy

\begin{matrix} {max}_{}^{} (\frac{1}{q_{1}} d_{1} (R), \frac{1}{q_{2}} d_{2} (R), \frac{1}{q_{3}} d_{3} (R)) \end{matrix}

is fogy. Tehát tényleg a csak (15) alatti

Q

pont lehet minimizáló.
Említsük meg végül az előbbi tétel egy érdekes következményét. A

{P_{1} P_{2} P_{3}}_{▵}

egy

S

pontját nevezzük nevezetes pontnak, ha van oly extremumfeladat, melynek csak az előírt

S

pont tesz eleget. A fenti

q_{v}

-k gyanánt

\begin{matrix} q_{v} = d_{v} (S) \end{matrix}

értékeket választva

Q = S

-re és csak erre lesz

\begin{matrix} {max}_{}^{} (\frac{d_{1} (Q)}{d_{1} (S)}, \frac{d_{2} (Q)}{d_{2} (S)}, \frac{d_{3} (Q)}{d_{3} (S)}) | \end{matrix}

minimális, ebben az értelemben a háromszög minden pontja nevezetes pont!
A hamutálcától indultunk és eljutottunk a szélsőértékfeladatok egy osztályához, melyeket minimax-feladatoknak nevezünk. Ezen feladatokhoz eljuthattunk volna egy egészen más feladatból kiindulva is. Ha egy kertben bizonyos számú fát akarunk ültetni, ezek ültetésének főszempontja az, hogy gyökereik egymás elől lehetőleg ne szívják el a talaj tápnedveit. Itt a fákat pontoknak tekintve ezeket úgy kell elhelyezni, hogy minden kettő lehetőleg messze legyen egymástól, aminek matematikai megfogalmazása úgy szól, hogy

\begin{matrix} {min}_{}^{}_{i \neq k}^{} \bar{P_{i} P_{k}} \end{matrix}

maximális legyen. Ez azonban sokkal nehezebb az előbbi feladatoknál és általában nincs is megoldva. A minimax-feladatok a felsőbb matematikában egyre jelentősebb szerepet játszanak a múlt század közepe óta, úgy hogy hasznosnak és érdekesnek tartom, hogy ezekre már ilyen elemi fokon is rá lehet irányítanom a figyelmet.