|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Bizonyos típusú szélsőértékfeladatokról I.
Egy korábbi előadásban mondanivalómat azon közhiedelem eloszlatására szántam, hogy a matematikai problémák vagy mind meg vannak oldva, vagy csak nagyon távoli és mesterkélt kérdések várnak még megoldásra. Ezen előadásban arra szeretnék egy példa kapcsán rámutatni, hogy a matematikai magvú problémák a hétköznapi életben is szinte az utcán hevernek és mint lesz egy ilyen matematikai problémává.
Egy társaság ül a kávéházban egy asztal körül, mindenki dohányzik és egyetlen hamutálca van. Rögtön felvetődő kérdés, hova tegyük ,,a lehető legméltányosabban'' a hamutartót. A matematikus rögtön érzi, hogy a dolog lényegében matematikai probléma, csak ki kell hámozni a matematikai lényeget. De mi az, hogy a ,,lehető legméltányosabban''? Hogy mindegyiknek a lehető legkevesebbet kelljen nyújtózkodnia? Ehhez mindenesetre tudni kell az egyes emberek távolságát a hamutálcától. De a hamutálca kiterjedt; mely pontjának távolsága számít? Az ember távolsága melyik pontjától számít? Itt jön a feladat matematikaivá alakításának első lépése; a hamutálcát és az embereket pontoknak tekintjük. A hamutálcát reprezentáló pont az asztalon van; de hol vegyük fel az embereket reprezentáló pontokat? A matematikai feladattá-alakítás második lépéseként vegyük fel a személyeket reprezentáló pontokat az asztal határgörbéjén. Ezáltal legalább az egyes embereknek a hamutálcától való távolságai meghatározott értelemmel bírnak és így a ,,legméltányosabb'' elhelyezés diszkutálása egyáltalán megkezdődhetik. A matematikus azonban tapasztalatból tudja, hogy egy kérdés vizsgálatát célszerű egy lehetőleg egyszerű eseten kezdeni. Egy ilyen volna jelen esetben az, amikor a társaság csak két tagból áll, kezdjük azzal.
Ez esetben a megoldás igen egyszerűnek látszik; a két embert jelölő két pont felezőpontjába kell a hamutálcát helyezni. Ezen megoldás ellen két kifogás emelhető. Az egyik az, hogy nem biztos, hogy a hamutálcát így elhelyezve, az az asztalra esik. Nem igaz ugyanis az, hogy egy görbe két pontját összekötő szakasz felezőpontja a görbe belsejébe esik; ilyen görbére az 1. ábrán látható példa. 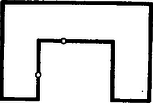 1. ábra
Még csak az sem mondható, hogy ilyen alakban nem raknak asztalokat. Tehát egy további egyszerűsítő feltevéssel élünk az asztal alakjára vonatkozólag és az asztalt köralakúnak tételezzük fel; ekkor az első kifogás elesik. A második a ,,méltányosság'' kérdése. A két ember egyikének karja lehet lényegesen hosszabb, mint a másiké; ez esetben a rövidebb karú bizonyos joggal gondolhatja, hogy az a méltányos, ha a hamutálcát hozzá annyiszor közelebb rakják, ahányszor az ő karja rövidebb a másikénál. Ha a két ember közül az egyik lényegesen idősebb, mint a másik, méltányosnak tekintheti, hogy a kort valamilyen kulcs szerint tekintetbe vegyék. Már ezen példák is mutatják, hogy a ,,legméltányosabb'' elhelyezésnél rendkívül sok szempontot kellene figyelembe venni; amit tehetünk, az csak az, hogy e sok szempont közül a leglényegesebbeket vesszük tekintetbe, melyek mellett a megfelelő matematikai feladatokat jelenlegi tudásunk alapján meg tudjuk oldani. A matematikai nehézségek már az esetben jelentkeznek, mely eset tárgyalására most rátérünk és amelynél tovább nem is megyünk.
Az előbbiek szerint úgy látszik, hogy ez esetben a feladatnak a következő két matematikai formája lehet:
a) Ha a karhosszaktól eltekintünk, akkor a feladat: keresni az embereket jelző , , pontoktól egyenlő messze fekvő pontot.
b) Ha a karhosszakat is tekintetbe vesszük és ezek hosszai , akkor a feladat: keresni egy olyan pontot, amelyre Azonban könnyű látni, hogy ezek különös konklúzióhoz vezethetnek. Az a) esetben legyen tompaszögű. Ekkor a szóbanforgó pont nyilván a körülírt kör középpontja, ill. az asztalé. Ha azonban az asztal sugara nagy, akkor a hamutálca mindegyiktől igen messze esne, azaz ez esetben a legméltányosabb elhelyezés mindhárom dohányzó számára igen kényelmetlen megoldás egyben. Mivel a b) forma az a)-t tartalmazza esetére, tehát b)-re ugyanez áll. Mi lehet tehát az a) és b) követelmények helyett annak matematikai megfogalmazása, hogy a hamutálca mindenki számára a ,,lehető legkényelmesebben'' legyen elhelyezve? Próbáljuk meg azt követelni, hogy a dohányosok egyikének se kelljen. ,,túl'' messzire nyúlnia. Ez az első méltányossági definíciót alapul véve azt követeli, hogy a szakaszok maximuma minimális legyen, azaz -t úgy kell választani, hogy minimális legyen, vagy keresendő Hasonlóképp a második méltányossági definíciót alapul véve az optimális -t a | | (3) |
minimumát szolgáltató pont által próbáljuk megadni, vagyis keresni a | | (4) |
értékét. Mivel (3)‐(4) nyilván magában foglalja (1)‐(2)-t, elég ezzel foglalkozni. A (3) minimumát adó pontot, ha van ilyen, minimizálónak fogjuk nevezni.
A feladat tárgyalása tisztán elemi geometriai úton is lehetséges volna, ad hoc e feladatra csinált gondolatmenettel. Ehelyett egy más utat fogunk követni, mely a hasonló feladatok egész körére alkalmazható. Ehhez első lépésként azt állítjuk, hogy a (3)-at minimizáló pont, ha létezik, nem lehet a háromszögön kívül. Ha ugyanis ezen a háromszögön kívül van, akkor tekintsük a háromszög egy olyan oldalát, amely -t elválasztja a háromszögtől; legyen ez pl. . Ekkor -t a -ből -re bocsátott merőlegesen a háromszöghöz közelítve -nek -től, -től és -tól való távolságai mind csökkennek, azaz a (3) érték csökken. Tehát ha a minimizáló pont létezik, csak belsejében vagy kerületén lehet.
Azt állítjuk továbbá, hogy ahhoz, hogy a belsejében levő pont a kívánt minimumot adja, szükséges, hogy fennálljon | | (5) |
Legyen ugyanis olyan pont, amelyre (5) nem áll fenn; ekkor a csúcsok jelölését alkalmasan választva vagy | | (6) |
vagy | | (7) |
áll fenn. A (6) esetben -t közelítsük -hoz ,,egy kissé'', -be; ezáltal fogyott ,,egy kicsit''. Az és értékek esetleg nőttek ,,egy kicsit'', de, ha -t ,,elég kevéssel'' változtattuk meg, akkor még mindig kisebbek az és távolságok, mint , ez pedig határozottan kisebb, mint . A (6) esetben tehát
és így nem lehet a kívánt minimumot adó pont. A (7) eset kényesebb, mert ott -t úgy kell elmozdítani, hogy és mindkettője fogyjon; ez azonban elérhető, ha pl. -t a -ből -ra bocsátott merőleges mentén mozgatjuk el ,,egy kicsit'' és ugyanúgy járunk el, mint előbb. Ezáltal (5) be van bizonyítva.
Nézzük hasonlóképp, mi a szükséges feltétele annak, hogy a minimum egy kerületi -re éressék el. Ha egy kerületi pontra akkor -t ismét a felé közelítve ,,egy kissé'', adódik, mint előbb, hogy nem lehet minimizáló pont. Hasonlóképp látható be, hogy ha és a kerületen van, de nincs a szakaszon, akkor nem lehet minimizáló pont. Ahhoz tehát, hogy a minimizáló pont a kerületen legyen, szükséges, hogy a szakaszon legyen és | | (8) |
legyen.
Adott , és mellett nevezzük a háromszöget ,,jó''-nak, ha kerületén nincs (8) tulajdonságú pont, különben ,,rossz''-nak. tehát akkor és csak akkor ,,jó'', ha a
relációkkal -n, ill. -on, ill. -en egyértelműleg meghatározott , és pontokra
Előbbiek szerint tehát ,,jó'' esetén (8) elesik, azaz ez esetben ahhoz, hogy minimizáló pont legyen, (5) fennállása szükséges. 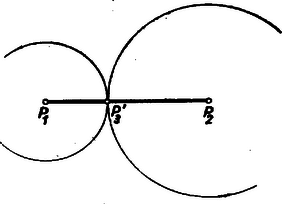 2. ábra
Legyen most ,,rossz''. Ez esetben azt állítjuk, hogy a belsejében (5) nem teljesülhet, amiből következni fog, hogy ez esetben ahhoz, hogy minimizáló pont legyen, szükséges, hogy a kerületen legyen és (8) fennálljon. Ugyanis, ha pl. | |
akkor a minden belső pontjára vagy vagy vagy ezek mindkettője áll. Azaz minden belső pontra
és így belső pont nem lehet minimizáló. Ebből az állítás következik.
Feladatunk teljes megoldásától azonban még távol vagyunk.
Középiskolai délutánon tartott előadás, Budapesten a Bolyai János Matematikai Társulatban, 1957: okt. 12-én.Turán Pál: Az egész számok bizonyos számsorozatairól, e Lapok 8. köt. (1954) 33-41. old.65Szokás véges sok szám közt az előforduló legnagyobb, illetőleg legkisebb értéket a | |
jellel jelölni. Hasonlóan jelölhető végtelen sok szám közül a legkisebb, ha van ilyen (az számok közt pl. sem legnagyobb, sem legkisebb nem szerepel). Ha ez a végtelen sok érték egy változó mennyiséghez, pl. egy pont lehetséges helyzeteihez van egyértelműen hozzárendelve, vagyis minden ponthoz tartozik egy f() számérték (pl. a , , szám), akkor a ,,'', vagy ,,'' jel után f-t írjuk és a jel alá a változó mennyiség jelét, mint (2)-ben is tettük. Ha ez a változó csak bizonyos korlátok közt változhat, ezt is feltüntethetjük. Pl. egy adott középpontú, sugarú kör belsejében felvett minimum így jelölhető;
|
 PDF | MathML
PDF | MathML