| Cím: | A tetraéder nevezetes pontjairól (2. befejező közlemény) | ||
| Szerző(k): | Molnár Ferenc | ||
| Füzet: | 1958/február, 33 - 38. oldal |  PDF | MathML PDF | MathML |
|
| Témakör(ök): | Szakmai cikkek | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. 3. Lényeges eltérést tapasztalunk a háromszögektől a tetraéder magasságvonalainak (a tetraéder csúcsaiból a szemközti lapokra bocsátott merőleges egyeneseknek) vizsgálatánál. Míg a háromszög magasságvonalai mindig egy pontban (a háromszög magasságpontjában) metszik egymást, a tetraéder négy magasságvonala általában nem rendelkezik ezzel a tulajdonsággal. Sőt általában még az sem teljesül, hogy a tetraéder két magasságvonala metszi egymást. Bebizonyítjuk ugyanis a tetraéder magasságvonalainak következő tulajdonságát: A tetraéder két csúcsából kiinduló magasságvonalak akkor és csak akkor metszik egymást, ha a csúcsokat összekötő él merőleges a szemközti élre. Bizonyítás. Jelöljük -vel, ill. -vel az , ill. csúcsból kiinduló magasságvonalak talppontját a szemközti lapon (8. ábra). 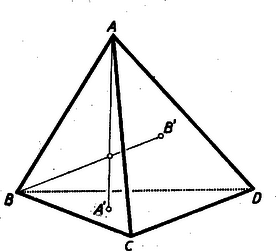 Ha és metszik egymást, akkor egy síkban vannak; ez a sík merőleges a , ill. síkokra, hiszen tartalmazza az ezekre merőleges , ill. egyenest; tehát merőleges a és síkok metszésvonalára is; mivel pedig tartalmazza az egyenest, kapjuk, hogy Megfordítva, tegyük fel, hogy és merőlegesek egymásra. Mivel az magasságvonal merőleges a síkra, tehát merőleges -re is. Innen adódik, hogy merőleges az síkra, hiszen két egyenesére merőleges. Hasonlóan kapjuk, hogy merőleges az síkra is. Mivel pedig az egyenesen keresztül egyetlen -re merőleges sík fektethető, az és síkok azonosak, vagyis és egy síkban vannak, tehát metszik egymást (párhuzamosak nem lehetnek, mert egymással nem párhuzamos tetraéderlapokra merőlegesek). A fenti tételből közvetlenül adódik a tetraéder magasságvonalainak a következő tulajdonsága: Ha a tetraéder két magasságvonala metszi egymást, akkor a másik kettő is metszi egymást. Ha pl. az és pontokból kiinduló magasságvonalak metszik egymást, akkor az él merőleges a élre. De ekkor egyúttal a él is merőleges az élre, ez pedig az előző tétel értelmében biztosítja a és csúcsokból kiinduló magasságvonalak metszését. Ha e két metszéspont egybeesik, akkor a tetraéder négy magasságvonala egyetlen közös ponton megy át; ezt a pontot a tetraéder magasságpontjának nevezzük. A két metszéspont azonban általában különböző; a magasságpont létezésére a következő szükséges és elégséges feltétel mondható ki: A tetraédernek akkor és csak akkor van magasságpontja, ha a szemközti élek páronként merőlegesek egymásra. A feltétel szükségessége nyilvánvaló. Ha ugyanis van magasságpont, akkor mindegyik magasságvonal metszi mindegyiket ugyanabban a pontban, tehát a magasságvonalakra vonatkozó első tételből adódik, hogy bármelyik él merőleges a szemköztire. Megfordítva, ha a szemközti élek merőlegesek egymásra, akkor bármely két magasságvonal metszi egymást. Ekkor viszont egy térbeli egyenesekre vonatkozó általános tételből következik (l. a 471. gyakorlatot), hogy a magasságvonalak vagy mind egy síkban vannak, vagy egy ponton mennek át. De egy síkban nem lehetnek, mert akkor a tetraéder csúcsai is egy síkban lennének, tehát egy ponton mennek át, és így van magasságpont. Megemlítjük, hogy a tétel kimondásánál túl sokat követeltünk meg. Elég annyit feltenni, hogy a tetraéder három szemközti élpárja közül kettő merőleges egymásra, ebből a harmadik szemközti élpár merőlegessége már következik. Legyen pl. 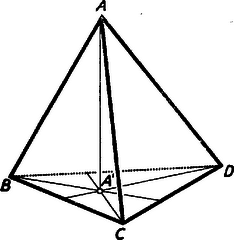 Hasonlóan adódik és merőlegességéből, hogy is magasságvonal a háromszögben, amiből következik már, hogy a háromszög magasságpontja. Ekkor viszont , és mivel , következik, hogy merőleges az síkra, tehát merőleges az ezen síkban fekvő egyenesre is, és ezt akartuk bizonyítani. A magasságponttal rendelkező tetraédert ortocentrikus tetraédernek nevezzük (ortocentrum=magasságpont). A fenti bizonyításból kiolvashatjuk az ortocentrikus tetraédernek azt a tulajdonságát, hogy csúcsainak a szemközti lapokon levő merőleges vetületei a lapok magasságpontjai. Ezt figyelembe véve könnyű megadni olyan tetraédert, melynek egyik szemközti élpárja merőleges egymásra, de nincs magasságpontja. Ilyen pl. az a tetraéder, melynek alapja a (nem derékszögű, de különben tetszőleges) háromszög, negyedik csúcsának, -nak a szemközti lapon levő merőleges vetülete megegyezik a háromszög valamelyik csúcsával, pl. -vel. Ennél a tetraédernél nyilván merőleges -re, de a többi szemközti élek nem merőlegesek egymásra, tehát nincs magasságpont. Az ortocentrikus tetraéder nemcsak a szemközti élek merőlegességével jellemezhető. Fennáll ugyanis a következő tétel: A tetraéder akkor és csak akkor ortocentrikus, ha a szemközti éleinek felezőpontjait összekötő egyenesszakaszok (a tetraéder éltengelyei) egyenlők. Bizonyítás. Tegyük fel, hogy az tetraéder ortocentrikus. Jelöljük az élek felezőpontjait a 10. ábra szerint , , , , , -tal. 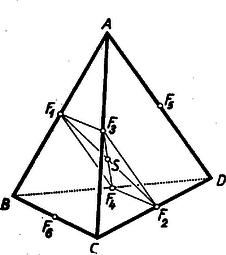 Tudjuk, hogy a szemközti élek felezőpontjait összekötő egyenesszakaszokat, pl. -t és -et a súlypont felezi, amiből következik, hogy parallelogramma, melynek középpontja S.4 Mivel a tetraéder ortocentrikus, szemközti élei, pl. és merőlegesek egymásra. De és merőlegességéből következik a velük párhuzamos és oldalak merőlegessége is, amiből viszont adódik, hogy téglalap. Mivel pedig a téglalap átlói egyenlők, kaptuk, hogy . Hasonlóan adódik, hogy , amiből már következik, hogy az ortocentrikus tetraéder mindhárom éltengelye egyenlő hosszúságú. Megfordítva, tegyük fel, hogy a tetraéder éltengelyei egyenlő hosszúságúak. Ez azt jelenti, hogy pl. az parallelogramma átlói egyenlők, amiből következik, hogy az téglalap. De ekkor és , és így a velük párhuzamos és élek is merőlegesek egymásra. Hasonlóan kapjuk, hogy a tetraéder másik két szemközti élpárja is merőleges egymásra, tehát a tetraéder ortocentrikus. Megemlítjük a kapott tételnek egy érdekes következményét. Mivel az ortocentrikus tetraéder éltengelyei egyenlő hosszúságúak, és a súlypont az éltengelyeket felezi, a súlypont egyenlő távol van a tetraéder élfelezőpontjaitól. Más szóval, ortocentrikus tetraédernél a hat élfelezőpont egy gömbön helyezkedik el, melynek középpontja a súlypont. Ezt a gömböt nevezzük az ortocentrikus tetraéder második Feuerbach-gömbjének. (Az elnevezés indokolását lásd később.) 4. Ismeretes a háromszögnek az a nevezetes tulajdonsága, hogy a magasságpont, a súlypont és a körülírt kör középpontja egy egyenesen van, mégpedig a súlypont a másik kettő által meghatározott szakasznak a körülírt kör középpontjához közelebbi harmadolópontja. Ezt az egyenest a háromszög Euler-egyenesének nevezzük. A tetraéder fenti nevezetes pontjai is rendelkeznek hasonló tulajdonsággal. (A következőkben feltesszük, hogy a tetraédernek van magasságpontja, vagyis ortocentrikus.) Ortocentrikus tetraédernél a magasságpont , a súlypont és a körülírt gömb középpontja egy egyenesen van; a súlypont a másik kettő által meghatározott szakasz felezőpontja. Ezt az egyenest a tetraéder Euler-egyenesének nevezzük. A bizonyításnál fel fogjuk használni a háromszög Euler-egyenesére vonatkozó tételt. Jelöljük a tetraéder magasságpontjának merőleges vetületét a tetraéder valamelyik, pl. lapján -gyel, a körülírt gömb középpontjának merőleges vetületét ugyanezen a lapon -gyel. A magasságpontnak és a körülírt gömb középpontjának vizsgálatánál láttuk, hogy a háromszög magasságpontja, a körülírt kör középpontja. Az egyenesen, a háromszög Euler-egyenesén rajta van a háromszög súlypontja. Mivel továbbá az pont egyúttal a tetraéder csúcsának is merőleges vetülete a lapon, a tetraéder súlyvonala, és így az ezen levő súlypont is az és pontokkal együtt benne van az egyenesen átmenő, a síkra merőleges síkban (11. ábra). 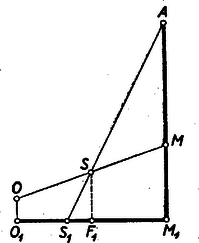 Tudjuk, hogy az súlypont az súlyvonalat negyedeli, az pont pedig az egyenest harmadolja, következésképpen -nek a lapon levő merőleges vetülete az egyenesszakasz felezőpontja (l. az ábrát). Kaptuk tehát, hogy az , , pontoknak a tetraéder tetszőleges lapján levő merőleges vetületei egy egyenesbe esnek, mégpedig az pont vetülete a másik két vetületi pontot összekötő szakasz felezőpontja. Ebből viszont már következik, hogy az , , pontok is egy egyenesbe esnek és az szakasz felezőpontja. (Ehhez elég lenne annyit tudni, hogy az , , pontok vetületei két tetraéderlapon egy egyenesbe esnek, ebből már következik, hogy rajta vannak a vetületekben állított merőleges síkok metszésvonalán.) Ez az egyenes éppen a tetraéderlapok Euler-egyeneseiben ezekre a lapokra állított merőleges síkok közös egyenese, más szóval a tetraéder Euler-egyenesének merőleges vetületei a tetraéderlapok Euler-egyenesei. 5. Végül vizsgáljuk a háromszög Feuerbach-körének (az oldalfelezőpontokon átmenő körnek) megfelelőjét a tetraédernél. A Feuerbach-kör fogalmát kétféleképpen is általánosíthatjuk ortocentrikus tetraéderre. Ha figyelembe vesszük, hogy a háromszög oldalfelezőpontjai az oldalak súlypontjai, akkor ezeknek megfeleltethetjük a tetraéder lapsúlypontjait. Így a Feuerbach-kör első általánosításaként adódik a tetraéder lapsúlypontjai által meghatározott gömb. Ezt a gömböt a tetraéder első Feuerbach-gömbjének nevezzük. A háromszög oldalfelezőpontjainak másrészt megfeleltethetjük a tetraéder éleinek felezőpontjait is. Így a Feuerbach-kör második általánosításaként adódik az ezek által meghatározott gömb. Ezzel a gömbbel már találkoztunk, és éppen ezt neveztük második Feuerbach-gömbnek. Az elnevezést az indokolja, hogy ez a gömb a Feuerbach-kör egyik általánosítása. Ismeretes, hogy a háromszög Feuerbach-köre a következő tulajdonságokkal rendelkezik: középpontja az Euler-egyenesen a körülírt kör középpontja és a magasságpont által meghatározott szakasz felezőpontja, sugara a körülírt kör sugarának fele, átmegy a magasságvonalak talppontjain, valamint a magasságpontot a háromszög csúcsaival összekötő szakaszok felezőpontjain. A háromszög Feuerbach-körének ezen tulajdonságait a tetraéder első Feuerbach-gömbje örökli, ami mutatja, hogy ez a gömb a Feuerbach-kör közvetlen megfelelője (ez indokolja az első elnevezést is). Bebizonyítjuk ugyanis, hogy az első Feuerbach-gömb a következő tulajdonságokkal rendelkezik: középpontja az Euler-egyenesen az szakasz -hez közelebbi harmadolópontja, sugara a tetraéder köré írt gömb sugarának harmada, átmegy a tetraéder magasságvonalainak talppontjain (a lapok magasságpontjain), végül a magasságpontot a csúcsokkal összekötő szakaszokat a magasságponthoz közelebbi harmadolópontokban metszi. Mivel az első Feuerbach-gömb ezen utóbbi nyolc ponton kívül definíció szerint tartalmazza a négy lapsúlypontot is, szokás ezt a gömböt a tizenkét pont gömbjének nevezni. A bizonyításnál hasonló módon járhatunk el, mint a háromszög Feuerbach-körére vonatkozó tétel egyik bizonyításánál. Az első Feuerbach-gömb a lapsúlypontok által meghatározott tetraéder köré írt gömb. Mivel az súlypont a tetraéder súlyvonalait negyedeli, kapjuk, hogy az tetraéder az tetraédernek az középpontból történő egyharmadára való zsugorításával és -re való tükrözésével keletkezik. Ebből következik, hogy a Feuerbach-gömböt az tetraéder köré írt gömbnek -ből történő egyharmadára való zsugorításával és -re való tükrözésével kapjuk, tehát középpontja rajta van az egyenesen, mégpedig az egyenesnek -től számítva -val ellentétes oldalán, és . Innen felhasználásával adódik, hogy 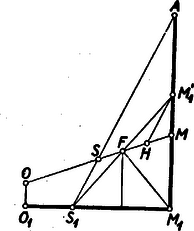 Végül a tételben kimondott utolsó tulajdonság igazolásához elegendő ismét az pontot az egyik, pl. csúccsal összekötő szakasz -hez közelebbi harmadolópontjáról kimutatni, hogy a Feuerbach-gömbön van. Ennek igazolásához jelöljük az szakasznak az -hez közelebbi harmadolópontját -val. Mivel az háromszögben az és oldalak harmadolópontjait köti össze, kapjuk, hogy Befejezésül megemlítjük a tetraéder második Feuerbach-gömbjének egy tulajdonságát. Mivel a tetraéder bármelyik lapját határoló élek felezőpontjai a második Feuerbach-gömbön vannak, az illető háromszöglap síkja a gömböt a háromszög Feuerbach-körében metszi. Ebből viszont, figyelembe véve a háromszög Feuerbach-körének tulajdonságait, következik, hogy a második Feuerbach-gömb átmegy a tetraéderlapok magasságvonalainak talppontjain, valamint bármelyik lap magasságpontját az illető lap csúcsaival összekötő szakaszok felezőpontjain. 4Az a tény, hogy parallelogramma, következik abból is, hogy az háromszögben, a háromszögben a oldallal párhuzamos középvonal, és így |