Cím: A tetraéder nevezetes pontjairól (1. közlemény)
Szerző(k):  Molnár Ferenc 
Füzet: 1958/január, 1 - 6. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A térgeometria egyik érdekes feladata annak vizsgálata, hogy az egyes síkbeli alakzatoknak és azok tulajdonságainak milyen alakzatok és ezeknek milyen tulajdonságai felelnek meg a térben. A legegyszerűbb sokszögnek, a háromszögnek térbeli megfelelője a tetraéder vagy háromoldalú gúla.1 Ebben a cikkben a háromszög nevezetes egyeneseinek és pontjainak a tetraédernél található megfelelőit vizsgáljuk. Látni fogjuk, hogy a háromszög nevezetes egyeneseinek és pontjainak megfelelői általában megtalálhatók a tetraédernél is, és ezek hasonló tulajdonságokkal rendelkeznek, mint a háromszög nevezetes egyenesei és pontjai. Ezen tulajdonságok körét azonban a tetraéder térbeli mivoltából adódó olyan tulajdonságokkal is ki fogjuk egészíteni, amelyek a háromszögnél nem lépnek fel.
1. A háromszög súlyvonalainak mintájára beszélhetünk a tetraéder súlyvonalairól. A tetraéder súlyvonalainak nevezzük a tetraéder csúcsait a szemközti háromszöglapok súlypontjaival összekötő egyeneseket. A tetraéder súlyvonalai a háromszög súlyvonalaihoz hasonló tulajdonsággal rendelkeznek:

 

A tetraéder négy súlyvonala egy pontban metszi egymást; ez a pont a súlyvonalakat a csúcstól számítva 3:1 arányban osztja (a súlyvonalak ,,negyedelőpontja''). Ezt a pontot a tetraéder súlypontjának nevezzük.
 

Bizonyítás. Jelölje a tetraéder A, B, C, D csúcsaival szemközti lapok súlypontjait rendre S1, S2, S3, S4. Válasszunk ki két tetszőleges súlyvonalat, pl. 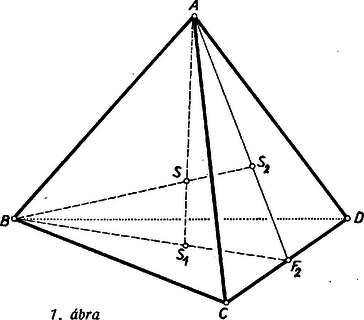AS1-et és BS2-t (1. ábra).
 
 
1. ábra
 

S1 ill. S2 rajta van a BCD háromszög BF2, ill. az ACD háromszög AF2 súlyvonalán (F2 a CD él felezőpontja), tehát az AS1 és BS2 súlyvonalak benne vannak az A, B és F2 pontok által meghatározott síkban, és így szükségképpen metszik egymást egy S pontban. Az ABF2 háromszögben S1, ill. S2 a BF2, ill. AF2 oldalakat F2-ből kiindulva harmadolja, tehát S1S2 párhuzamos az AB oldallal és annak harmadrésze. Innen adódik, hogy az ABS és S1S2S háromszögek hasonlók, mégpedig az S1S2S háromszög az ABS háromszögnek S középpontból történő harmadára való kicsinyítésével és S-re vonatkozó tükrözésével keletkezik, amiből következik, hogy SS1 az AS, SS2 a BS szakasz harmada, vagyis S az AS1 és BS2 súlyvonalak negyedelőpontja. Mivel bármely két súlyvonal metszéspontja mindegyiknek negyedelőpontja, és minden súlyvonalnak egyetlen negyedelőpontja van, így mind a négy súlyvonal egyetlen közös ponton megy át, mely mindegyiknek negyedelőpontja.
A fenti tétel bizonyítását felhasználva bebizonyítjuk a súlypontnak egy további érdekes tulajdonságát:
 

A tetraéder szemközti éleinek felezőpontjait összekötő egyenesek a tetraéder súlypontján mennek át. A súlypont a szemközti élek felezöpontjait összekötő egyenesszakaszok felezőpontja.
 

Bizonyítás. Jelöljük a tetraéder két szemközti élének, pl. AB-nek és CD-nek felezőpontját F1-gyel és F2-vel. Az előző tétel bizonyításánál szereplő ABF2 háromszögben az F1F2 egyenes az F2 csúcsból kiinduló súlyvonal, tehát az AB-vel párhuzamos S1S2 egyenesszakaszt is annak F3 felezőpontjában metszi (2. ábra).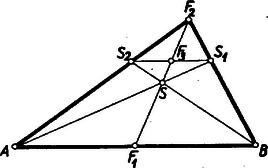
 
 
2. ábra
 

Az F1F2 egyenes tehát összeköti az ABS és S1S2S hasonló háromszögek egymásnak megfelelő AB és S1S2 oldalainak F1 és F3 felezőpontjait, következésképpen átmegy a háromszögek S hasonlósági pontján, a tetraéder súlypontján. Mivel S a két említett háromszög hasonlósági pontja, adódik továbbá, hogy S az F1F3 szakasznak is negyedelőpontja. Másrészt az S1 és S2 harmadolópontokat összekötő szakasz az F1F2 szakaszt is az F3 harmadolópontban metszi. E két utóbbi tényből viszont már következik, hogy S az F1F2 szakasz felezőpontja. Mivel mindez elmondható a tetraéder bármely két szemközti élének felezőpontjait összekötő szakaszról, állításunkat bizonyítottuk.
 

2. A háromszög további nevezetes pontjai a körülírt kör középpontja, a beírt kör középpontja, valamint a hozzáírt körök (a háromszög egy‐egy oldalát kívülről érintő körök) középpontjai. Ezek megfelelői is megtalálhatók a tetraédernél.
A háromszög köré írt kör középpontját az oldalfelező merőlegesek metszéspontja szolgáltatta. A háromszög oldalfelező merőlegeseinek a tetraédernél megfelelnek az élek felezőpontjain átmenő és az élekre merőleges síkok (az élek felező merőleges síkjai), ugyanis a térben két ponttól egyenlő távolságra levő pontok mértani helye éppen ez a sík. Ezen síkok hasonló tulajdonsággal rendelkeznek, mint a háromszög oldalfelező merőlegesei. Fennáll ugyanis a következő tétel:
 

A tetraéder éleinek felező merőleges síkjai egy ponton mennek át; ez a pont egyenlő távol van a tetraéder csúcsaitól, tehát a tetraéder köré írt gömb középpontja.
 

Bizonyítás. Vegyük a tetraéder egyik lapját, pl. BCD-t határoló élek felező merőleges síkjait. Ezen síkok pontjai rendre egyenlő távol vannak a B és C, C és D, D és B csúcsoktól, tehát BCD háromszög síkját a háromszög oldalfelező merőlegeseiben metszik. Következésképpen mindhárom sík átmegy ezek közös pontján, a háromszög köré írt kör középpontján. Mivel továbbá ezek a síkok merőlegesek a BCD síkra (ugyanis a BCD sík tartalmazza a rájuk rendre merőleges BC, CD, DB egyeneseket), így mindhárom sík tartalmazza a BCD háromszög köré írt kör középpontjában a háromszög síkjára állított merőleges egyenest. Ennek pontjai az előbbiek szerint egyenlő távol vannak a B, C, D csúcsoktól. Messük el most ezen egyenest a tetraéder egy további élének, pl. AB-nek felező merőleges síkjával. Mivel ez utóbbi sík pontjai egyenlő távol vannak az A és B csúcsoktól, a kapott metszéspont egyenlő távol van mind a négy csúcstól, tehát rajta van az AC és AD élek felező merőleges síkjain is.
A fenti bizonyításból azt is leolvashatjuk, hogy a tetraéderlapok köré írt körök középpontjaiban a lapokra állított merőleges egyenesek egy ponton, a tetraéder köré írt gömb középpontján mennek át. Más szóval, a tetraéder köré írt gömb középpontjának a tetraéderlapokon levő merőleges vetületei a háromszöglapok köré írt körök középpontjai.
A háromszögbe beírt kör középpontját a belső szögfelezők metszéspontja szolgáltatta. A háromszög belső, ill. külső szögfelezőinek a tetraédernél megfelelnek a belső, ill. külső lapszögek szögfelező síkjai (lapszögfelező síkok), ugyanis két síktól egyenlő távolságra levő pontok mértani helyét ezek a síkok adják. A tetraéder lapszögfelező síkjai a háromszög szögfelezőihez hasonló tulajdonsággal rendelkeznek:
 

A tetraéder belső lapszögjelező síkjai egy ponton mennek át; ez a pont egyenlő távol van a tetraéder lapjaitól, tehát a tetraéderbe beírt gömb (a tetraéder lapjait belülről érintő gömb) középpontja.
 

Bizonyítás. Vegyük a tetraéder egyik csúcsában, pl. A-ban találkozó lapok belső szögfelező síkjait. Az AB élen átmenő belső lapszögfelező sík pontjai egyenlő távol vannak az ABC és ABD síkoktól, az AC élen átmenő belső lapszögfelező sík pontjai az ABC és ACD síkoktól. Ebből adódik, hogy a két sík metszésvonalának pontjai egyenlő távol vannak az ABC, ABD, ACD síkoktól, következésképpen ez az egyenes rajta van az AD élen átmenő belső lapszögfelező síkon is. Azt kaptuk tehát, hogy az A csúcsban találkozó három belső lapszögfelező sík egy egyenesben metszi egymást. Messük el most ezen egyenest a tetraéder egy további élén, pl. BC-n átmenő belső lapszögfelező síkkal. Ezen sík pontjai egyenlő távol vannak az ABC és BCD síkoktól, tehát a kapott metszéspont, amely mindig a tetraéder belsejében van, egyenlő távol van mind a négy tetraéderlaptól, és így rajta van a CD és DB éleken átmenő belső lapszögfelező síkokon is.
A háromszög oldalait kívülről érintő körök megfelelői is megtalálhatók a tetraédernél. Vegyük ugyanis pl. a tetraéder A csúcsában találkozó három belső lapszögfelező sík közös egyenesét, és messük el azt most a tetraéder egy további élén, pl. BC-n átmenő külső lapszögfelező síkkal. Az előző tétel bizonyításához hasonlóan adódik, hogy a kapott metszéspont egyenlő távol van a tetraéder összes lapjaitól. Másrészt a pont nyilván a tetraéderen kívül, abban a végtelenbe nyúló térrészben helyezkedik el, melyet a BCD sík, valamint a többi tetraéderlapoknak a BC, CD, DB éleken túli meghosszabbításai határolnak. Ez a pont tehát rajta van a CD és DB éleken átmenő külső lapszögfelező síkokon is, és a tetraéder BCD lapját kívülről, valamint a többi lapok meghosszabbításait érintő gömb (a BCD laphoz hozzáírt gömb) középpontja. Ilyen hozzáírt gömb a tetraéder minden lapjához található, tehát összesen négy van.
A háromszögnél a beírt kör és a hozzáírt körök az összes érintőkört szolgáltatják. Ez nyomban belátható, ha meggondoljuk, hogy a háromszög oldalegyeneseinek meghosszabbításai a síkot hét részre darabolják szét, de ezek között csak négy olyan van, amelyet mindhárom oldal vagy azok meghosszabbítása határolja (3. ábra; I, II, III, IV síkrészek), márpedig érintőkörök csak ezekben a síkrészekben lehetnek.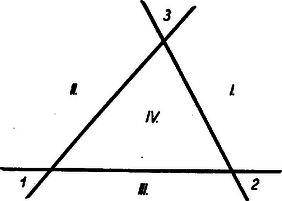
 
 
3. ábra
 

Ha most vizsgáljuk a tetraéder lapjain átfektetett síkok által szétdarabolt teret, a kapott térrészek közül csak azokban található érintőgömb, amelyeket mind a négy sík határol. Az előbbiekben öt ilyen térrészt már találtunk, itt helyezkednek el a beírt gömb és a hozzáírt gömbök. A többi térrészek között vannak a tetraéder ,,csúcsokon túli meghosszabbításai'', amelyek megfelelnek a háromszög szögeihez tartozó csúcsszögtartományoknak (a 3. ábrán az 1, 2, 3-mal jelölt síkrészek). Egy ilyen végtelenbe nyúló térrészt a tetraéder valamelyik csúcsában találkozó lapjainak a csúcson túli meghosszabbításai határolnak. Ezekben nem lehetnek érintőgömbök, mert mindegyiket csak három sík határolja. Fennmaradnak még a tetraéder ,,éleken túli meghosszabbításai''. Egy ilyen térrészt a tetraéder valamelyik élében találkozó két lapjának az élen túli meghosszabbításai, valamint a másik két lapon átfektetett síkok határolnak. Mindegyik élhez tartozik egy ilyen ,,vályúszerű'' végtelenbe nyúló térrész, mindegyiket mind a négy tetraéderlapon átfektetett sík határolja, tehát tartalmazhatnak érintőgömböt. (A BC és AD élekhez tartozó ''vályúszerű térrészeket'' lásd a 4. ábrán.)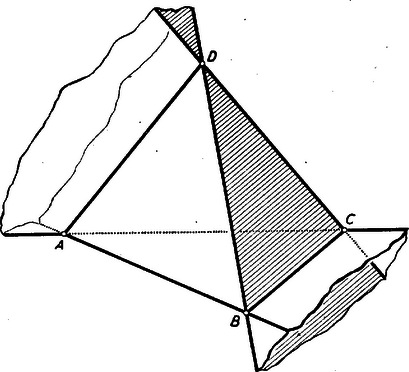
 
 
4. ábra
 

A kapott hat térrész közül azonban csak három tartalmaz olyan gömböt, amely a tetraéder összes lapjainak meghosszabbításait érinti (külső érintőgömb). Ugyanis a tetraéder két szemközti éléhez, pl. a BC-hez és AD-hez tartozó ,,vályúszerű térrészekben'' levő külső érintőgömbök középpontjainak rajta kell lenniök a BC és AD éleken átmenő belső szögfelező síkok metszésvonalán, valamint egy további élen, pl. AB-n átmenő külső szögfelező síkon (hiszen pl. az AB-n átmenő belső szögfelező síknak az előbbi egyenessel való metszéspontja a tetraéderen belül lenne, és így a beírt gömb középpontját adná). Aszerint tehát, hogy ez utóbbi síknak az előbbi szögfelező síkok metszésvonalával alkotott metszéspontja a BC vagy az AD élhez tartozó ,,vályúszerű térrészben'' van, az egyik vagy másik térrészben kapunk külső érintőgömböt. (Ez a metszéspont valóban külső érintőgömb középpontja, hiszen egyenlő távol van a tetraéder összes lapjaitól, és így szükségképpen rajta van az AC, CD, DB éleken átmenő külső szögfelező síkokon is). Azt kaptuk tehát, hogy a tetraéder két szemközti éléhez tartozó ,,vályúszerű térrészek'' egyikében lehet csak külső érintőgömb, tehát összesen három külső érintőgömbhöz juthatunk.2
Összefoglalva megállapíthatjuk, hogy a tetraédernek általában nyolc érintőgömbje van (beírt gömb, négy hozzáírt gömb, három külső érintőgömb). Az érintőgömbök sugarai között hasonló összefüggések találhatók, mint a háromszögnél (l.a 878. feladatot).
A tetraédernél felmerül egy újabb érintőgömb lehetősége. Feltehető a kérdés, van-e olyan gömb, amely a tetraéder összes éleit belső pontban érinti (élérintő gömb). Látni fogjuk, hogy ilyen gömb általában nem létezik. Annak megállapítására, hogy milyen esetben létezhetik ilyen gömb, vegyünk egy olyan tetraédert, amelynek van élérintő gömbje, és vizsgáljuk meg, milyen összefüggést állapíthatunk meg ebből a feltételből kiindulva. Jelölje a gömb érintési pontjait a tetraéder élein E1, E2, E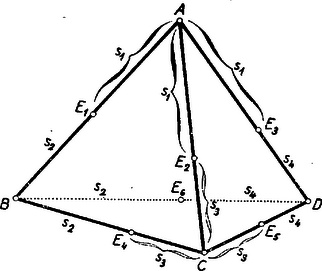3, E4, E5, E6 (5. ábra).
 
 
5. ábra
 

Mivel külső pontból a gömbhöz húzott érintőszakaszok hossza egyenlő,3
így ezek a pontok az éleket olyan szakaszokra osztják, amelyek között fennállnak a következő egyenlőségek:
AE1=AE2=AE3=s1,BE1=BE4=BE6=s2,CE2=CE4=CE5=s3,DE3=DE5=DE6=s4.
Vizsgáljuk a szemközti élek összegét. Ezekre a fenti egyenlőségeket felhasználva kapjuk, hogy
AB+CD=BC+AD=AC+BD=s1+s2+s3+s4;
vagyis megállapíthatjuk, hogy az élérintő gömbbel rendelkező tetraéder szemközti éleinek összege mindhárom élpárra ugyanakkora.
Ez utóbbi tulajdonság általában nem teljesül, tehát a tetraédernek általában nincs élérintő gömbje. Vegyünk ugyanis pl. egy olyan tetraédert, melynek alapja szabályos háromszög (BCD), negyedik csúcsának, A-nak a BCD lapon levő merőleges vetülete megegyezik a BCD háromszög valamelyik csúcsával, pl. B-vel (7. ábr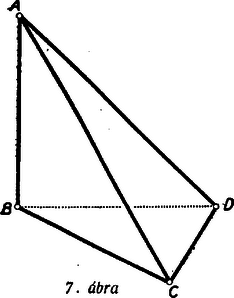a).
 
 

Ennél a tetraédernél az alapélek egyenlők, az ezekkel szemközti oldalélek közül AC és AD egyenlők egymással, AB viszont ezektől különböző, tehát a szemközti élek összege is különböző:
AB+CD≠AC+BD=AD+BC.

Bebizonyítható, hogy az élérintő gömb létezésére kapott feltétel nemcsak szükséges, hanem elegendő is, vagyis ha a tetraéder szemközti éleinek összege mindhárom élpárra ugyanakkora, akkor rendelkezik élérintő gömbbel. Ennek a tételnek az igazolását az olvasóra bízzuk (l. a 879. feladatot).
1A következőkben mindig általános (nem csupán szabályos) tetraéderről lesz szó.

2Megjegyezzük, hogy nem minden tetraédernél található külső érintőgömb, hiszen pl. a BC és AD éleken átmenő belső szögfelező síkok metszésvonala párhuzamos is lehet az AB-n átmenő külső szögfelező síkkal. Az olvasó könnyen meggyőződhet róla, hogy a szabályos tetraéder például ilyen tulajdonságú.

3Ez utóbbi azonnal belátható, ha meggondoljuk, hogy az O középpontú, KE érintőszakasszal rendelkező kört az OK tengely körül megforgatva (6. ábra) gömböt kapunk, a KE szakasz megforgatásával pedig a K pontból a gömbhöz húzott érintőket kapjuk.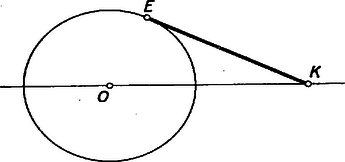

 
 
6. ábra