Kezdőlap


Cím:	Az 1957. évi Arany Dániel matematikai tanulóverseny: (3., befejező közlemény)
Füzet:	1957/november, 89 - 96. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbiakban közöljük a haladók (II. osztályosok) versenyén kitűzött feladatok megoldásait.

I. forduló

1. feladat. Egy vonat elindul

A

-ból és egyenletes mozgással halad

B

felé.

11

perccel később elindul

B

-ből egy vonat ugyanazon az útvonalon, ugyancsak állandó sebességgel

A

felé. A találkozástól számítva

20

, ill.

45

perc múlva érnek a vonatok

B

-be, ill.

A

-ba. Milyen arányban osztja a

T

találkozási pont az

AB

távolságot?

I. megoldás: Ha az

A

-ból induló vonat sebessége

v_{1}

B

-ből indulóé

v_{2}

, akkor a találkozás utánra vonatkozó adatokból

\begin{matrix} 20 v_{1} = T B, 45 v_{2} = T A, amiből \frac{A T}{T B} = \frac{9}{4} \cdot \frac{v_{2}}{v_{1}} . \end{matrix}

Viszont a

T

-ig megtett utakhoz szükséges időket számítva ki, ezek különbsége

11

perc, vagyis

\begin{matrix} \frac{A T}{v_{1}} - \frac{T B}{v_{2}} = 11. \end{matrix}

Ide

T A

és

T B

imént kapott értékét behelyettesítve, és a

\frac{v_{2}}{v_{1}} = u

értékkel végig szorozva, utóbbira a

\begin{matrix} 45 u^{2} - 11 u - 20 = 0 \end{matrix}

egyenletet kapjuk. Innen, csak a pozitív gyököt véve figyelembe,

\begin{matrix} u = \frac{4}{5}, és így \frac{A T}{T B} = \frac{9}{4} u = \frac{9}{5} . \end{matrix}

II. megoldás: Legkönnyebb arra az időre egyenletet felírni, amely valamelyik vonatnak indulástól a

T

pontba jutásig vagy az egész út megtételéhez szükséges. Ebben még a szemléletet is segítségül vehetjük, mert közelebbi adatok nélkül is vázolhatjuk a viszonyokat szemléltető grafikon szerkezetét (lásd az 1. ábrát, amelyen vízszintesen az időt, függőlegesen a megtett utat ábrázoltuk).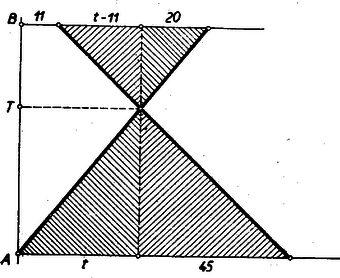

1. ábra

Ha pl. az

A

-ból induló vonat

T

-be érkezéséhez szükséges

t

időt akarjuk kiszámítani, akkor az ábrán azonosan sraffozott hasonló háromszögekből

\begin{matrix} \frac{t}{20} = \frac{45}{t - 11} . \end{matrix}

Az egyenlet mindkét oldalán éppen (a kiszámítható arány áll.) Átrendezve (ha

t \neq 11

)

\begin{matrix} t^{2} - 11 t - 900 = 0, \end{matrix}

és az egyenlet pozitív gyöke

\begin{matrix} t = \frac{11 + 61}{2} = 36, \end{matrix}

a keresett arány pedig

\begin{matrix} \frac{A T}{T B} = \frac{t}{20} = \frac{9}{5} . \end{matrix}

A fent említett 3 további időtartam bármelyikéből indulva ki teljesen hasonlóan járhatunk el.

III. megoldás: Közvetlenül a keresett

x = A T / B T

arányra is állíthatunk fel egyenletet. Az

A

-ból induló vonat ugyanis

20 x

perc alatt érkezik

A

-ból

T

-be, a

B

-ből induló pedig

45 / x

perc alatt

B

-ből

T

-be. A feladat első része szerint pedig

\begin{matrix} 20 x - \frac{45}{x} = 11 azaz 20 x^{2} - 11 x - 45 = 0. \end{matrix}

Innen, csak a pozitív gyököt véve tekintetbe

\begin{matrix} x = \frac{11 + 61}{40} = \frac{9}{5} . \end{matrix}

2. feladat. Egy

a

oldalú négyzet két szomszédos oldalát

6

, ill.

10

egyenlő részre osztjuk, majd összekötjük a közös csúcstól

\frac{3}{6}

távolságban levő első osztáspontot a szomszédos oldalnak a közös csúcstól számított negyedik osztáspontjával. Bizonyítsuk be, hogy az így nyert összekötő egyenes érinti a négyzetbe írható kört.

I. megoldás: Válasszuk a négyzet oldalának felét mértékegységül. Legyenek a négyzet

A

csúcsából induló oldalakon a beírt kör érintési pontjai

U

V

, a kör középpontja

K

, az

A U

szakaszon

A B = \frac{1}{3}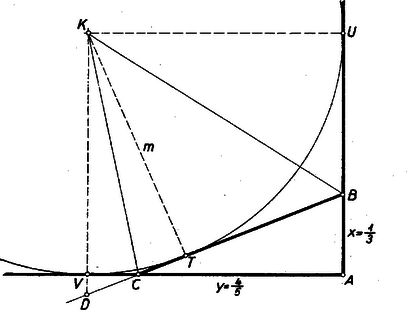

, az

A V

-n

A C = \frac{4}{5}

(2. ábra).

2. ábra

Azt kell megmutatni, hogy

B C

távolsága

K

-tól

1

, amit úgy is fogalmazhatunk, hogy a

B C K

háromszög

K

-ból húzott

K T = m

magassága egységnyi. Ezt a magasságot a háromszög területének meghatározásán keresztül számíthatjuk ki könnyen. Az

A B C

B K U

C K V

háromszögek területei rendre

\begin{matrix} \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{4}{5} = \frac{2}{5}, \frac{1}{2} \cdot 1 \cdot \frac{2}{3} = \frac{1}{3}, \frac{1}{2} \cdot 1 \cdot \frac{1}{5} = \frac{1}{10}, \end{matrix}

és így a

B C K

háromszög t területére

\begin{matrix} t = 1 - \frac{2}{15} - \frac{1}{3} - \frac{1}{10} = \frac{13}{30} . \end{matrix}

Pythagoras tételével kiszámítva a

B C

oldalt

\begin{matrix} B C^{2} = {(\frac{1}{3})}^{2} + {(\frac{4}{5})}^{2} = \frac{25 + 144}{9 \cdot 25} = {(\frac{13}{15})}^{2}, azaz B C = \frac{13}{15} . \end{matrix}

Így

\begin{matrix} m = \frac{2 t}{B C} = 1. \end{matrix}

És ez volt a bizonyítandó.

II. megoldás: Az előző megoldás jelöléseit használjuk. Legyen

K V

és

B C

metszéspontja

D

(2. ábra). Kiszámíthatjuk

K T

-t hasonló háromszögekből is. Az

A B C

és

T D K

háromszögek hasonlók, így

\begin{matrix} \frac{K T}{K D} = \frac{C_{A}}{C_{B}} . \end{matrix}

(1)

B C

-re, mint az előző megoldásban, Pythagoras tétele segítségével

13 / 15

adódik. Mivel az

A B C

és

V D C

háromszögek is hasonlók, azért

\begin{matrix} \frac{V D}{V C} = \frac{A B}{A C}, amiből V D = \frac{A B}{A C} = \frac{1}{3} \cdot \frac{5}{4} \cdot \frac{1}{5} = \frac{1}{12}, \end{matrix}

és így (1)-ből

\begin{matrix} K T = \frac{C A}{C B} \cdot K D = \frac{4}{5} \cdot \frac{15}{13} \cdot (1 + \frac{1}{12}) = \frac{4}{5} \cdot \frac{15}{13} \cdot \frac{13}{12} = 1. \end{matrix}

Ezzel az állításunkat igazoltuk.

III. megoldás: Jelöljük a négyzet oldalát

a

-val, egyébként használjuk az előbbi jelöléseket. A feladatnál általánosabban számítsuk ki, hogy az

A U

egyenes egy

A

-tól

x

távolságban levő

B

pontjából a négyzetbe írt körhöz húzott érintő mekkora

y

szakaszt metsz le az

A V

egyenesből (2. ábra).
Az érintkezés folytán

\begin{matrix} T B = B U = \frac{a}{2} - x, T C = C V = \frac{a}{2} - y . \end{matrix}

Így Pythagoras tétele szerint

\begin{matrix} x^{2} + y^{2} = {(\frac{a}{2} - x + \frac{a}{2} - y)}^{2} = a^{2} - 2 a x - 2 a y + x^{2} + y^{2} + 2 x y, \end{matrix}

azaz

\begin{matrix} a^{2} - 2 a x - 2 a y + 2 x y = 0. \end{matrix}

Innen

y

egyértelműen meghatározható

x

-hez. Az ilyen

y

távolságban metsző egyenes lehet csak a kör érintője. Mivel pedig

B

-ből (

B U

-n kívül) pontosan egy érintő húzható a körhöz, így ez szükségképpen az

A V

-t

A C = y

távolságban metsző egyenes lesz.
A nyert egyenlet mindkét oldalához

a^{2}

-et hozzáadva, a következő áttekinthetőbb alakra jutunk:

\begin{matrix} (q - x) (a - y) = \frac{a^{2}}{2} . \end{matrix}

Ez tehát a szükséges és elégséges feltétele annak, hogy az

a

oldalú négyzet egyik csúcsából induló oldalakat e csúcstól

x

és

y

távolságban metsző egyenes érintse a négyzetbe írt kört. Ez

x = \frac{a}{6}

esetben éppen

y = \frac{2 a}{5} = \frac{4 a}{10}

-et ad, amivel a feladat állítását igazoltuk.

Megjegyzés: Az ábránk ugyan csak pozitív,

\frac{a}{2}

-nél kisebb

x

y

értékekre vonatkozik, de könnyen belátható, hogy tetszés szerinti pozitív vagy negatív értékekre is ugyanez a szükséges és elégséges kritérium adódik, ha az

A U

-val, illetőleg

A V

-vel ellentétes irányú szakaszokat tekintjük negatívnak.

IV. megoldás: Mérjük rá egy

A B C D

négyzet minden csúcsából az egyik oldalra egy irányban körülhaladva az oldal hatodrészét, majd ellenkező irányban körüljárva az oldal

2 /

5 részét. Ha az egy-egy csúcshoz közelebb eső osztópontokat összekötjük, egy újabb, az előbbivel közös középpontú

A' B' C' D'

négyzetet kapunk. Ha megmutatjuk, hogy a két négyzet egybevágó, akkor a beírt körük közös, s így igazolást nyer a feladat állítása (3. ábra).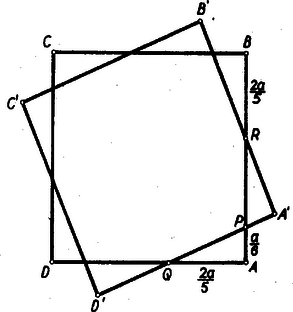

3. ábra

Az egybevágósághoz elég megmutatni, hogy a négyzetek egymásból egybevágó derékszögű háromszögeket metszenek le. Mivel e háromszögek hasonlósága nyilvánvaló, elég egy oldalpárjukról, pl. az átfogókról megmutatni, hogy egyenlők. Jelöljük a négyzet oldalát

a

-val. Az

A

csúcsú derékszögű háromszög átfogójára Pythagoras tételével adódik

\begin{matrix} P Q = \sqrt[]{\frac{a^{2}}{3 b} + \frac{4 a^{2}}{25}} = \frac{13}{30} a . \end{matrix}

Viszont az

A'

csúcsú háromszög átfogója

\begin{matrix} P R = a - \frac{a}{6} - \frac{2 a}{5} = \frac{13}{30} a . \end{matrix}

Ezzel feladatunk állítása igazolást nyert.

Megjegyzés: Ha általában

A P = x

A Q = B R = y

, akkor a fenti megoldás azt adja, hogy a két négyzet akkor és csak akkor egybevágó, ha

\begin{matrix} x^{2} + y^{2} = {(a - x - y)}^{2}, \end{matrix}

és ez megegyezik az előző megoldásban nyert egyenlőséggel. Így az ott levezetett kritériumnak egy kevesebb számolást igénylő származtatásához jutunk.

3. feladat. Bizonyítsuk be, hogy

\begin{matrix} 9^{n + 2} + 10^{2 n + 1} \end{matrix}

osztható

91

-gyel, ha

n

tetszés szerinti nem negatív egész szúm.

I. megoldás: Az állítást teljes indukcióval igazolhatjuk.

n = 0

-ra a

\begin{matrix} 9^{2} - 10 = 91 \end{matrix}

számot kapjuk.
Ha valamilyen

n = k

értékre már tudjuk, hogy

\begin{matrix} 9^{k + 2} + 10^{2 k + 1} = 91 \cdot A, \end{matrix}

akkor

n = k + 1

-re

\begin{matrix} 9^{(k + 1) + 2} + 10^{2 (k + 1) + 1} = 9 \cdot 9^{k + 2} + 10^{2 k + 3} = 9 \cdot 91 A - 9 \cdot 10^{2 k + 1} + 10^{2 k + 3} = \\ = 91 \cdot 9 A + 10^{2 k + 1} (10^{2} - 9) = 91 \cdot (9 A + 10^{2 k + 1}), \end{matrix}

tehát az állítás

n = k + 1

-re is igaz. Ezzel igazoltuk az állítás helyességét minden nem negatív egész

n

-re.

II. megoldás: A vizsgálandó kifejezést átalakítjuk:

\begin{matrix} 9^{n + 2} + 10^{2 n + 1} = 81 \cdot 9^{n} + 10 \cdot 100^{n} = 91 \cdot 9^{n} + 10 (100^{n} - 9^{n}) . \end{matrix}

Az első tag osztható

91

-gyel, a második tagban zárójelben szereplő különbség osztható az alapok különbségével, azaz

100 - 9 = 91

-gyel. Így az összeg is osztható

91

-gyel.

Megjegyzés: Sok más hasonló átalakítás is elvezet az állítás igazolásához.

II. forduló

1. feladat. Oldjuk meg a következő egyenletrendszert:

\begin{matrix} x + y + z & = 12, & (1) \\ x^{2} + y^{2} + z^{2} & = 230, & (2) \\ x y & = - 15. & (3) \end{matrix}

I. megoldás: Küszöböljük ki (1) segítségével (2)-ből

z

-t. Rendezve és

2

-vel osztva

\begin{matrix} x^{2} + x y + y^{2} - 12 x - 12 y = 43. \end{matrix}

x^{2}

-tel szorozva, és a (3) egyenletet felhasználva az

\begin{matrix} x^{4} - 12 x^{3} - 58 x^{2} + 180 x + 225 = 0 \end{matrix}

(4)

egyenlethez jutunk. Ennek az első két tagja megegyezik az

x^{2} - 6 x

kifejezés négyzetének első két tagjával; utolsó két tagja pedig a

6 x + 15

(vagy

- 6 x - 15

) négyzetének utolsó két tagjával. Mind a négy tag előfordul tehát az

x^{2} - 6 x - 15

polinom négyzetében. Az egyenlet baloldala tehát így alakítható át:

\begin{matrix} {(x^{2} - 6 x - 15)}^{2} - 64 x^{2} = (x^{2} - 14 x - 15) (x^{2} + 2 x - 15) . \end{matrix}

x

-re tehát 4 értéket kapunk: az

\begin{matrix} x^{2} - 14 x - 15 = 0 és az x^{2} + 2 x - 15 = 0 \end{matrix}

egyenletek gyökeit:

x = 15

- 1

;

3

- 5

. Minden

x

-hez

y

-t a (3) és

z

-t az (1) egyenletből egyértelműen meghatározhatjuk, A lehetséges megoldások

\begin{matrix} I. & II. & III. & IV. \\ x= & 15, & - 1, & 3, & - 5, \\ y= & - 1, & 15, & - 5, & 3, \\ z= & - 2, & - 2, & 14, & 14. \end{matrix}

Ezek könnyen láthatólag (2)-t kielégítik.

Megjegyzés: Próbálgatással hamar rátalálunk a (4) egyenletnek a

- 1

gyökére. Másrészt

x

és

y

szimmetrikus szerepe miatt ugyanennek az egyenletnek tesznek eleget

y

gyökei is. Kell tehát, hogy a

- 1

-hez (3)-ból adódó

y = 15

érték is gyöke legyen az egyenletnek, ami így is van. Ennek alapján is eljuthatunk az egyenletnek a fenti megoldásban használt felbontásához.

II. megoldás: Az (1) egyenlet négyzetéből levonva a (2)-t, és (3) kétszeresét, majd

2

-vel osztva az

\begin{matrix} (x + y) z = - 28 \end{matrix}

(5)

egyenlethez jutunk: A

z

és

x + y = u

ismeretlenekre tehát az

\begin{matrix} u + z = 12 & (5') \\ u z = - 28 & (1') \end{matrix}

egyenletek állnak fenn. Így

z

és

u

\begin{matrix} v^{2} - 12 v - 28 = 0 \end{matrix}

egyenlet két gyöke, bármilyen sorrendben. Mivel

v_{1} = 14

és

v_{2} = - 2

, azért

x

és

y

\begin{matrix} x + y = 14, x y = - 15 vagy x + y = - 2, x y = 15 \end{matrix}

egyenletrendszernek tesznek eleget. Ezek a fentebb már szerepelt

\begin{matrix} t^{2} - 14 t - 15 = 0, ill. t^{2} + 2 t - 15 = 0 \end{matrix}

egyenletekre vezetnek (ott

t

helyett

x

-szel jelöltük az ismeretlent), s így az előbbi megoldásban talált gyökökhöz jutunk. Ezek kielégítik az (1), (3), (5) egyenleteket. Mivel azonban ezekből (2) következik [ha (1) négyzetéből levonjuk (3) és (5) kétszeresét], azért kielégítik az eredetileg adott egyenletrendszert is.

2. feladat. Melyik az a két, a számsorban egymás után következő, páratlan szám, amelyeknek négyzetösszege

\frac{n (n + 1)}{2}

alaké; ahol

n

természetes szám.

Megoldás: Legyen a két szomszédos páratlan szám

2 k - 1

és

2 k + 1

, ekkor

\begin{matrix} {(2 k - 1)}^{2} + {(2 k + 1)}^{2} = \frac{n (n + 1)}{2} \end{matrix}

azaz

\begin{matrix} 16 k^{2} + 4 = n (n + 1) . \end{matrix}

Ezt

4

-gyel szorozva, és

1

-et hozzáadva

\begin{matrix} 64 k^{2} + 17 = {(2 n + 1)}^{2} \end{matrix}

(2 n + 1)

-et

m

-mel jelölve, innen

\begin{matrix} m^{2} - 64 k^{2} = (m + 8 k) (m - 8 k) = 17. \end{matrix}

Itt feltétel szerint

m

pozitív, tehát a bal oldal első tényezője is az, s így a másodiknak is annak kell lennie, és kisebbnek az első tényezőnél. Mivel

17

prímszám, az egyetlen lehetséges felbontás

\begin{matrix} m + 8 k = 17, m - 8 k = 1, és így 16 k = 17 - 1 = 16. \end{matrix}

Innen

\begin{matrix} k = 1, m = 2 n + 1 = 9, azaz n = 4. \end{matrix}

Valóban

\begin{matrix} 1^{2} + 3^{2} = \frac{4 \cdot 5}{2} . \end{matrix}

3. feladat. Rögzítsük az

ABC_{▵}

-nek az

A

és

B

csúcsát. Mi a mértani helye azon

C

pontoknak, amelyekre nézve a változó oldalak négyzetösszege

\begin{matrix} a^{2}+b^{2}=d^{2} \end{matrix}

ahol

d

egy megadott szakasz.

Megoldás: Megmutatjuk, hogy a feltételnek megfelelő háromszögek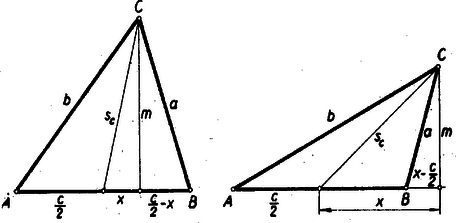

C

-ből induló súlyvonalai egyenlők. Legyen az

A B

oldal hossza

c

, és a

C

pont

A B

-n levő merőleges vetületének távolsága

A B

felezőpontjától

x

(4. ábra).

4. ábra

Ekkor Pythagoras tétele szerint

\begin{matrix} a^{2} = {(\frac{c}{2} - x)}^{2} + m^{2} = {(\frac{c}{2})}^{2} - c x + x^{2} + m^{2}, \\ b^{2} = {(\frac{c}{2} + x)}^{2} + m^{2} = {(\frac{c}{2})}^{2} + c x + x^{2} + m^{2}, \end{matrix}

és

\begin{matrix} m^{2} + x^{2} = s_{c}^{2} . \end{matrix}

Így

\begin{matrix} d^{2} = a^{2} + b^{2} = 2 {(\frac{c}{2})}^{2} + 2 (x^{2} + m^{2}) = 2 {(\frac{c}{2})}^{2} + 2 s_{c}^{2}, \end{matrix}

vagyis

\begin{matrix} s_{c}^{2} = \frac{d^{2}}{2} - {(\frac{c}{2})}^{2} . \end{matrix}

Ennek az értéknek pozitívnak kell lennie, különben nem lehetséges olyan háromszög, amely kielégíti a feladat feltételeit. Mivel itt

d

és

c

adott, azért

s_{c}

hossza független a

C

pont helyzetétől. Az összes megfelelő pontok tehát rajta vannak az

A B

szakasz felezőpontja körül

\begin{matrix} r = \sqrt[]{\frac{d^{2}}{2} - {(\frac{c}{2})}^{2}} \end{matrix}

sugárral rajzolt körön.
Legyen fordítva

C'

egy tetszés szerinti pont ezen a körön, távolsága

A

-tól, illetőleg

B

-től

b'

, ill.

a'

. Ekkor az

A B C'

háromszög

C'

-ből kiinduló súlyvonala

r

, s így a fenti képlet szerint

\begin{matrix} \frac{d^{2}}{2} - {(\frac{c}{2})}^{2} = r^{2} = \frac{{a'}^{2} + {b'}^{2}}{2} - {(\frac{c}{2})}^{2} \end{matrix}

amiből következik, hogy

\begin{matrix} {a'}^{2} + {b'}^{2} = d^{2}, \end{matrix}

tehát a

C'

pont megfelel a mértani hely feltételeinek.
A keresett mértani hely tehát az

A B

szakasz felezőpontja körül

r

sugárral rajzolt kör.