Cím: Az 1957. évi Országos Matematikai Tanulmányi Verseny II. (döntő) fordulója
Füzet: 1957/szeptember, 1 - 11. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A május 7-én lefolyt II. (döntő) fordulóban az alábbi három feladat volt kitűzve:
1. Bizonyítsuk be, hogy tetszés szerinti 1-nél nagyobb a számra

1log2a+1loga16≥1.

2. Egy háromjegyű számot egy kétjegyűvel elosztva, hányadosul az osztó számjegyeinek összegét kapjuk, a maradék pedig az osztó jegyeinek felcserélésével keletkező szám. Ha ezt a maradékot szorozzuk a hányadossal és hozzáadjuk az osztót, a keletkező szám az osztandó jegyeiből áll, de fordított sorrendben. Mi az osztandó és az osztó?
3. Egy sík egy szabályos négyoldalú gúla oldaléleit metszi. Bizonyítsuk be, hogy ha a gúla csúcsa S és a metszésidom az ABCD négyszög, akkor
1SA+1SC=1SB+1SD

Öt órai munkaidő után 121 iskola tanulói beadtak összesen 320 dolgozatot.
A Bolyai János Matematikai Társulat által a Művelődésügyi Minisztériummal egyetértésben kiküldött Központi Bizottság (Hódi Endre, Horvay Katalin, Késedi Ferenc, Lőrincz Pál és Neukomm Gyula előadó) Surányi János, a Társulat főtitkárának elnökletével a május 24-i ülésen a következő jelentést fogadta el:
,,A Bizottság megállapítja, hogy a versenyzők teljesítménye ‐ ha el is marad a tavalyitól ‐ teljesen kielégítő. Tavaly a feladatok puszta megoldása csak jó rutin munkát követelt, az idén mindhárom feladat (egyenlőtlenség, számelmélet, térmértan) olyan volt, hogy ezek megoldásához a tanulók az iskolában jó rutint nem szerezhettek. Ennek megfelelően a tavalyi 44 helyett ez idén csak 23 versenyző oldotta meg mind a három kitűzött feladatot, és amíg tavaly 2 teljes megoldás sem volt elég helyezés eléréséhez, addig ez idén az összes versenyzők, akik 2 feladatot lényegében megoldottak, helyezéshez jutottak. Hogy a feladatok ez idén nehezebbek voltak, mint tavaly, azt az is mutatja, hogy a döntőben 177 versenyző (55,3%) egy feladattal sem tudott megbirkózni; igaz, hogy ez elsősorban ‐ amint azt a Bizottság határozottan megállapította ‐ annak tulajdonítható, hogy az I. fordulóban észlelt ,,kollektív'' munka következményeként igen sok versenyző érdemtelenül került a döntőbe. A tanév csonkasága ‐ legalábbis az élcsoportban ‐ nem hagyott nyomot, ami bizonyára részben annak is köszönhető, hogy a Középiskolai Matematikai Lapok kiesés és redukció nélkül jelentek meg, és a 7. pontverseny teljes egészében folyik.
A dolgozatok elbírálásánál a Bizottság először a három feladat teljes, precíz megoldását követelte, ‐ előnyben részesítve azokat, amelyek kevesebb előismeretet tételeznek fel ‐ csak ez után vette figyelembe a többletmunkát.
Három helyes megoldáson felül többletmunkát mutatott fel 15 dolgozat.
Alapos megfontolás után a Bizottság Frivaldszky Sándor, Rockenbauer Antal és Böröczky Károly dolgozatát találta díjazásra érdemesnek. Az első kettő szabatos megoldást ad az 1. feladatra. A második feladatra Frivaldszky megoldása. precízebb, mint Rockenbaueré, viszont a 3. feladatra Rockenbauer egy hasonlóságon alapuló megoldáson kívül egy általánosítást is ad, míg Frivaldszky egyik megoldásában trigonometriai függvényt használ, egy második megoldásában pedig térbeli koordináta‐geometriához folyamodik. A Bizottság úgy találja, hogy e két dolgozat között megnyugtatóan dönteni nem tud, és így azt javasolja, hogy mindkettő egy‐egy I. díjban részesüljön. Böröczky a két első feladat szabatos megoldásán kívül az elsőre még egy kifogástalan második megoldást is ad. A 3. feladat állítását trigonometriai függvények nélkül bizonyítja némi többletmunkával. A Bizottság e dolgozatot 2. díjra javasolja.
A Bizottság 5 versenyzőt, akiknek dolgozata alig marad el a díjasokétól, I. dicséretre ajánl. Három feladat megoldásáért II. dicséretre ajánl a Bizottság 15 tanulót. Két feladat megoldásánál nagyobb teljesítményt ért el 9 résztvevő, két feladatot oldott meg, vagy ezzel egyenértékű teljesítményt nyújtott 21 tanuló és végül nem teljes két megoldást adott 28 tanuló. A Bizottság e három csoport tagjait rendre III., IV., ill. V. dicséretre javasolja.
 

A MM. a fenti javaslat alapján a következő döntést hozta:
 


1. díj (oklevél + 1000 Ft):
Frivaldszky Sándor (Bp. II., Rákóczi g. IV. o. t.)
Rockenbauer Antal (Bp. X., I. László g. IV. o. t.)
 


2. díj (oklevél + 500 Ft):
Böröczky Károly (Bp. XVIII., Steinmetz g. IV. o. t.)
 


I. dicséretben és nagyobb könyvjutalomban részesült:
 

Móricz Ferenc (Hódmezővásárhely, Bethlen G. g. IV. o. t.)
Pogány Eörs (Bp. V., Eötvös J. g. IV. o. t.)
Soós Tibor (Bp. I., Petőfi g. IV. o. t.)
Stahl János (Bp. VI., Kölcsey g. IV. o. t.)
Szatmáry Zoltán (Bp. VIII., Piarista g. IV. o. t.)
 


II. dicséretet és könyvjutalmat nyert:
 

Bergmann György (Bp. XIV., Abonyi u. ált. g. IV. o. t.), Borsi László (Bp. II., Rákóczi F. g. IV. o. t.), Ellmann Gábor (Bp. III., Arany J. g. III. o. t.), Gáspár János (Dombóvár, Gőgös g. IV. o. t.), Grell Mihály (Bp. XVI., Corvin Mátyás g. IV. o. t.), Győry Kálmán (Ózd, József A. g. III. o. t.), Hargitai Csaba (Bp. XXI., Jedlik g. IV. o. t.), Király Endre (Nagykőrös, Arany J. g. IV. o. t.), Makkai Mihály (Bp. V., Eötvös J. g. IV. o. t.), Montvay István (Bp. XIX., Landler g. III. o. t.), Papp Kálmán (Bp. IX., Fáy g. IV. o., t.), Pödör Bálint (Bp. II., Rákóczi F. g. III. o. t.), Ruppenthal Péter (Győr, Révai Miklós g. IV. o. t.), Simon László (Bp. XI., József A. g. III. o. t.), Verhás József (Bp. IV., Dózsa György g. IV. o. t.).
 


III. dicséretben és könyvjutalomban részesült:
 

Bácsy Ernő (Bp. VIII., Fazekas g. IV. o. t.), Csertag István (Bp. VIII., Széchenyi g. IV. o. t.), Galambos János (Veszprém, Lovassy L. g. III. o. t.), Jókúti Ferenc (Bp. VI., Kölcsey g. IV. o. t.), Kristóf László (Mosonmagyaróvár, Kossuth L. g. III. o. t.), Meskó Attila (Bp. VII., Madách g. III. o. t.), Parlagh Gyula (Kecskemét, Katona J. g. IV. o. t.), Salát Péter (Bp. XV., Dózsa György g. IV. o. t.), Solt György (Bp. VIII., Fazekas g. IV. o. t.).
 


IV. dicséretben és könyv jutalomban részesült:
 

Ádám Antal (Bp. VIII., Széchenyi g. IV. o. t.), Argay Gyula (Balassagyarmat, Balassa g. IV. o. t.), Behringer Tibor (Bp.. III., Árpád g. IV. a. t.), Dormány Mihály (Kecskemét, Katona J. g. IV. o. t.), Fekete Lajos (Debrecen, Ref. g. IV. o. t.), Fónyad Árpád (Bp. XVIII., Steinmetz g. IV. o. t.), Gáti Gyula (Debrecen, 3. sz. vegyip. t. IV. o. t.), Heinemann Zoltán (Pécs, Cséti bányaip. t. IV. o. t.), Hoffmann György (Bp. V., Eötvös J. g. IV. o. t.), Kalmár Ágota (Szeged, Ságvári g. III. o. t.), Kanyó Zoltán (Szeged, Radnóti g. III. o. t.), Károlyi Gyula (Zalaegerszeg, Zrínyi M. g. IV. o. t.), Kovács László (Bp., V., Eötvös J. g. IV. o. t.), Máté Levente (Szeged, Radnóti g. III. o. t.), Nyulász István (Bp., I., Petőfi g. IV. o. t.), Szalay Zsolt (Bp., VIII., Széchenyi g. III. o. t.), Szebeni András (Bp. I., Petőfi g. III. o. t.), Tokai József (Esztergom, I., István g. IV. o. t.), Trón Tibor (Debrecen, Fazekas g. III. o. t.), Váczy Pál (Debrecen, Ref. g. IV. o. t.), Vámos Attila (Bp. II., Rákóczi F. g. IV. o. t.).
 


V. dicséretet és könyvjutalmat nyert:
 

Ágh János (Bp. XIV., Petrik vegyip. t. III. o. t.), Baky Ágnes (Baja, III. Béla g. IV. o. t.), Csapody Miklós (Bp. VIII., Piarista g. IV. o. t), Detre Mária (Esztergom, Bottyán gépip. t. IV. o. t.), Detrekői Ákos (Szolnok, Verseghy F. g. III. o. t.), Fábry István (Bp. VIII., Széchenyi g. IV. o. t.), Fodor Lajos (Bp. XIX., Landler g. III. o. t.), Fuchs Péter (Győr, Révai Miklós g. IV.o. t.), Gergely Ervin (Bp. IV., Könyves Kálmán g. IV. o.t.), Glattfelder György (Pannonhalma, Bencés g. III. o. t.), Hank Zsombor (Szolnok, Verseghy F. g. III. o. t.), Kovács Zoltán (Szeghalom, Bolyai Farkas g. III. o. t.), Leipniker Péter (Makó, József A. g. III. o. t.), Lénárd Ágoston (Bp. IX., Puskás távközlési t. IV. o. t.), Literáthy Péter (Bp. XIV., Petrik vegyip. t. IV. o. t.), Makay Attila (Bp. IX., Fáy g. III. o. t.), Mató Gyöngyi (Bp. I., Szilágyi E. lg. IV. o. t.), Nagy Balázs (Eger, Dobó g. III. o. t.), Nagy Sándor (Szeghalom, Bolyai Farkas g. III. o. t.), Pataki Árpád (Nagyatád, ált. g. IV. o. t.), Pulay Péter (Bp. I., Petőfi g. III. o. t.), Sárközy András (Gyöngyös, Vak Bottyán g. III. o. t.), Schipp Ferenc (Mohács, Kisfaludy K. g. IV. o. t.), Szokoly Pál (Zalaegerszeg, Zrínyi M, g. IV. o. t.), Ujváry Menyhért Zoltán (Baja, 3. sz. építőip. t. III. o. t.), Várallyay László (Mosonmagyaróvár, Kossuth g. III. o. t.), Veress Péter (Pannonhalma, Bencés g. III. o. t.), Veszely Gyula (Kőszeg, ált g. IV. o. t.).
*

A verseny részletes eredményét megyék, városok és iskolafajok szerint a 4. oldalon közölt táblázat mutatja.
 

Kimutatás 1957. évi országos Matematikai Tanulmányi Verseny II. Fordulójáról

 


Beadott dolgozatok száma|EredményMegyék és városokgimn.ip. t.összesenDíjDicséretPontszám(nem hivatalos)isk.tan.isk.tan.  isk.tan.1.2.I.II.III.IV.V.g.i.t.  |össz.1.  Baranya.....11--11------11-1I.  Pécs város.....111324-----1--222.  Bács‐Kiskun.....51011611----1126173.  Békés.....46--46------22-24.Borsod.....49--49---1---4-4II.  Miskolc város.....241337----------5.Csongrád.....39--39--1---16-6  III.  Szeged város.....2912311-----3-6-66.Fejér.....1713210----------7.Győr‐Sopron.....625--625---11-411-118.Hajdú‐Bihar.....12--12-----v-----IV.  Debrecen város.....2934513-----4-6289.Heves.....26--26------22-210.Komárom.....3912411-----1121311.Nógrád.....13--13-----1-2-212.Pest.....41211513---1---4-413.Somogy.....35--35------11-114.Szabolcs.....33--33----------15.Szolnok.....915--915------22-216.Tolna.....22--22---1---4-417.Vas.....45--45------11-118.Veszprém.....714--714----1--3-319.Zala.....24--24-----113-3Vidék.....72170101982189--143121866672V. Budapest.....33121610391312141169101273130VÖsszesen.....105291162912132021515921281939202

 

* A gimnáziumokhoz sorolva 1 katonai középisk. 1 tanulóval.
 

A döntőben részt vett 320 tanuló közül 188 (58,8% ‐ tavaly 55,8%) volt lapunk munkatársa; a 81 helyezést elért tanuló közül azonban már 76 (93,8% ‐ tavaly 97,4%) volt feladatmegoldója lapunknak. (Részletes beszámoló ‐ sokféle szempontból ‐ a ,,Matematika tanítás''-ban jelenik meg.)
 

Alább közöljük a II. forduló feladatainak megoldását.
1. feladat.
 

I. megoldás: Kifejezzük a második tagot is 2 alapú logaritmussal. A logaritmus definíciója szerint, ha a≠1,
aloga16=16.
Ennek 2 alapú logaritmusát véve
loga16⋅log2a=4,vagyisloga16=4log2a.
Így az egyenlőtlenség bal és jobb oldalának, különbsége
1log2a+log2a4-1=4+(log2a)2-4log2a4log2a=(log2a-2)24log2a
Ez nem negatív, ha log2a pozitív, azaz, ha a>1, és ezt kellett bizonyítani.
 

Egyenlőség csak akkor áll fenn, ha log2a=2, azaz a=4.
 

II. megoldás: Vizsgáljuk valamivel általánosabban az
1logba+1logac
összeget, ahol vagy a, b, c>1 vagy 0<a, b, c<1 áll fenn. Jelöljük a két nevezőt u-val és v-vel, akkor a feltevés szerint u és v pozitív, s így a számtani és mértani közép közti egyenlőtlenség szerint
1u+1v≥21uv.
Mivel a logaritmus értelmezése szerint
bu=a,av=c,ezértbuv=(bu)v=av=c.
Innen
uv=logbc,
tehát azt nyertük, hogy a mondott feltételek esetén
1logba+1logac≥2logbc.
Ez b=2, c=16 esetén a bizonyítandó egyenlőtlenséget adja.
 

2. feladat.
 

Megoldás: A háromjegyű osztandó és a kétjegyű osztó jegyeit x, y, z, ill. u, v-vel jelölve, a feltételek a következő alakban írhatók:
100x+10y+z=(10u+v)(u+v)+10v+u,(1)100z+10y+x=(10v+u)(u+v)+10u+v,(2)
és mivel a maradék kisebb, mint az osztó, kell, hogy
u>v(3)
legyen. Az (1)-ből levonva a (2)-t
99(x-z)=9(u-v)(u+v)+9(v-u)=9(u-v)(u+v-1)(4)
adódik, azaz
11(x-z)=(u-v)(u+v-1).
A jobb oldal osztható 11-gyel. De u-v nem lehet osztható 11-gyel, mert mint számjegyek különbsége, 10-nél kisebb, és (3) szerint pozitív. A 11 viszont prímszám, s így tudjuk, hogy ha osztója egy szorzatnak, akkor osztója valamelyik tényezőnek is. Így u+v-1 osztható 11-gyel, de 2⋅11-nél kisebb, mert u és v számjegyek, és 0 sem lehet, mert akkor ‐ figyelembe véve (3)-at is ‐ 10u+v=10 volna, ami nem megoldása a feladatnak. Így u+v-1=11, azaz
u+v=12,(5)
és (1)-ből
100x+10y+z=(10u+v)⋅12+10v+u=(9u+12)⋅12+120-10u+u=264+99u.


A bal oldal kisebb, mint 1000, tehát
99u≤999-264,u≤72599=73299.
A (3) egyenlőséget és (5)-öt figyelembe véve, innen u=7, v=5 adódik. Ezt beírva (1) és (2) jobb oldalába
 

(10u+v)(u+v)+10v+u=75⋅12+57=957,
(10v+u)(u+v)+10u+v=57⋅12+75=759.
 

Így azt kaptuk, hogy a feladatnak egy megoldása van, melyben az osztandó 957, az osztó 75.
 

Megjegyzés: Az (5) összefüggés birtokában közvetlenül meg tudjuk állapítani x, y és z-t is. Összeadva az (1) és (2) egyenlőségeket, és felhasználva (5)-öt
101(x+z)+20y=11(u+v)(u+v)+11(u+v)=(6)=11(u+v)(u+v+1)=1716.

A bal oldal 20-szal osztva (x+z)-t, a jobb 16-ot ad maradékul, tehát e két szám csak 20 egy többszörösében különbözhet, de mivel x és z számjegyek azért
x+z=16(7)
kell, hogy legyen, és ezt (6)-ba írva
y=5
adódik. (4)-ből és (3)-ból következik, hogy szükségképpen
x>z.
16 két különböző egyjegyű összeadandóra csak 9+7 alakban bontható, tehát x=9, y=5, z=7, ebből (1) vagy (2) és (5) alapján u és v is meghatározható. A föntebb követett gondolatmenet azonban gyorsabban vezetett el a megoldáshoz.
 

3. feladat.
 

Sok versenyző használt trigonometriát a feladat megoldásában. Bemutatunk egy ilyen megoldást.
 

I. megoldás. Kiszámítjuk az 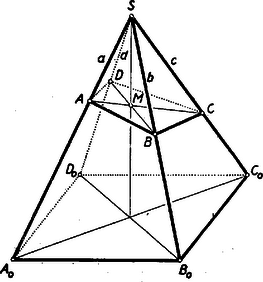SABCD gúla térfogatát egyrészt mint az SABC és SACD, másrészt mint az SABD és SBCD tetraéderek térfogatának összegét (1. ábra).
 
 
1. ábra
 

Az SA0B0C0D0 gúla S-ből húzott testmagassága egyenlő α szögeket zár be a gúla oldaléleivel, és benne van két‐két szemközti oldalél síkjában. Mivel az alaplap négyzet, a kérdéses testmagasság egyben merőleges vetülete is két szemközti oldalél síkjában a másik két oldalélnek. Így egy‐egy ilyen síkkal a másik két oldalél α nagyságú szöget zár be.
Jelöljük az SA, SB, SC, SD élhosszúságokat a, b, c, d-vel.
Az SABC tetraéder alaplapjának az SAC háromszöget választva, ennek S-nél levő szöge 2α, így az SA-ra C-ből bocsátott magasság hossza SC sin2α=csin2α, az alaplap területe tehát 12acsin2α. A B csúcsból az alapra bocsátott magasság hossza viszont bsinα. Így a tetraéder térfogatát V4-gyel jelölve
V4=16abcsin2αsinα.

Az első bekezdésben szereplő másik három tetraéder V2, V3, V1 térfogatára V2=16acdsin2αsinα, V3=16abdsin2αsinα, V1=16bcdsin2αsinα. A V1+V3=V3+V4 egyenletet 16abcdsin2αsinα értékkel osztva, a bizonyítandó
1a+1b=1c+1d
egyenletet kapjuk.
 

Megjegyzés: Ha a gúla alapja nem négyzet, hanem téglalap, akkor a fenti meggondolásban, csak annyi változik, hogy egy oldalél a két vele szomszédos oldalél síkjával, valamilyen α-tól különböző β szöget zár be, de ez az érték mind a négy oldalélre ugyanaz. Így a fentiekben a térfogatokban szereplő utolsó tényező sinα helyett sinβ lesz, ami a végkövetkeztetésen nem változtat. A feladat állítása tehát téglalap alapú egyenlő oldalélű gúlára is érvényes.
 

II. megoldás. A négyszögmetszet AC átlója benne van az SAC síkban, BD átlója pedig az SBD síkban, ezen átlók M metszéspontja tehát a két sík metszésvonalán van, az pedig az SA0B0C0D0 gúla S-ből induló testmagasságának egyenese, amely az oldalélekkel egyenlő α szögeket zár be (1. ábra). Így SM közös szögfelezője az ASC és BSD háromszögeknek, amelyeknek S-nél levő szöge egyaránt 2α.
Ha e két háromszöget 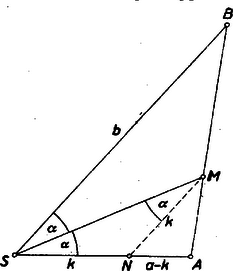SM körül egymásra forgatva képzeljük (ez az egymásra forgatás akkor is elvégezhető, ha az A0B0C0D0 alaplap téglalap), a feladat állítása a következő síkbeli állítássá fogalmazható át: Ha egy szög felező egyenesének egy pontján át húzott két szelő a szög száraiból a csúcstól számítva a és c, illetőleg b és d hosszúságú szakaszokat metsz le, akkor
1a+1c=1b+1d.
Ez még úgy is fogalmazható, hogy a szárakból lemetszett szakaszok reciprok értékeinek összege független a szelő irányától. Erre az állításra számos egyszerű, trigonometriát nem használó, megoldás adható.1)
Legyen ASB a kérdéses szög, a szögfelező messe az AB szakaszt M-ben (2. ábra).
 
 
2. ábra
 

Húzzunk M-en át párhuzamost BS-sel. Messe ez az SA-t N pontban. Az SNM háromszög S-nél és M-nél fekvő szöge egyaránt α, így a háromszög egyenlőszárú. Az egyenlő SN és MN távolságokat jelöljük k-val. Ekkor AN=a-k, és a hasonló ASB és ANM háromszögekből
ab=a-kk=ak-1.
Mindkét oldalhoz 1-et adva és a-val osztva
1a+1b=1k.
Mivel k hossza csak az SM hosszától és α nagyságától függ, az AB szelő irányától nem, így állításunkat bebizonyítottuk.
 

Megjegyzések: 1. Ha tetszés szerinti egyenlő oldalélű gúlát veszünk, akkor az alapsokszög körbeírható, a testmagasság talppontja e kör középpontja, és az oldalélek egyenlő α szöget zárnak be a testmagassággal. Ha még az alapsokszög szimmetrikus is a kör középpontjára, vagyis a szemközti csúcsokat összekötő átlók egy ponton, a kör középpontján mennek keresztül, akkor egy síkkal elmetszve ez összes oldaléleket, a keletkező sokszögmetszet szemközti csúcsait összekötő átlók is egy ponton mennek keresztül, és ez a pont a testmagasságon van. Így kiválasztva egy szemközti élpárt a rajtuk átfektetett síkban egy háromszög keletkezik, melyben a 2α szög felezőjének hossza a testmagasságnak a metsző síkig terjedő darabja, vagyis mindegyik háromszögben ugyanakkora. Így a bebizonyított tételt alkalmazhatjuk az összes szemközti élpárra és azt kapjuk:
Ha egy egyenlő oldalélű gúla alapja centrálisan szimmetrikus sokszög (és így szükségképpen páros oldalszámú), akkor egy minden oldalélt metsző síkot véve, a szemközti élpárokból lemetszett darabok reciprok értékeinek összege minden élpárra ugyanakkora.
2. A II. megoldásban bizonyított síkbeli tétel következik az 1905. évi Eötvös‐verseny 3. feladatának2) állításából is, mely szerint egy 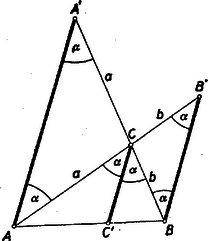ABC háromszög csúcsain át párhuzamosan elmetszve a szemközti oldaelegyeneseket, egy‐egy A', B', C' pontban, de úgy, hogy C' A és B közt legyen (3. ábra) fennáll az
1AA'+1BB'=1CC'
összefüggés.
 
 
3. ábra
 

Ha itt CC' a C csúcsú 2α szög szögfelezője, akkor az ACA' és BCB' háromszögek C-vel szemközti oldalán fekvő szögei α-val egyenlők. Így a két háromszög egyenlő szárú és egymáshoz hasonló. Ezért AC=CA'=a, BC=CB'=b és
aAA'=bBB'=r.
Innen AA'-t és BB'-t a fenti egyenletbe helyettesítve
ra+rb=1CC',azaz1a+1b=1r⋅CC'.
A jobb oldalon r csupán az α szög nagyságától függ, így mindazon háromszögekben, amelyek a 2α szögben és az ebből induló CC' szögfelező hosszában megegyeznek, a 2α szöget bezáró oldalak reciprok értékeinek összege egyenlő.
 

III. megoldás: A feladat állítását a testmagasság segítségül vétele nélkül is bebizonyíthatjuk.
Ha a metsző sík párhuzamos az alappal, akkor az oldalélekből egyenlő szakaszokat metsz le, s így a feladat állítása magától értetődő. Ha ez nem áll, akkor messe egymást, pl. 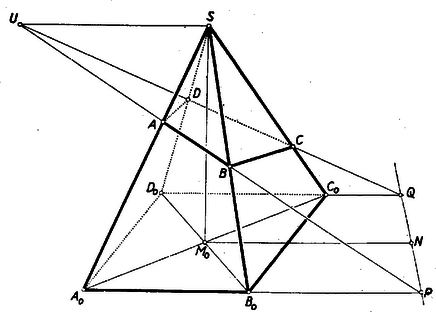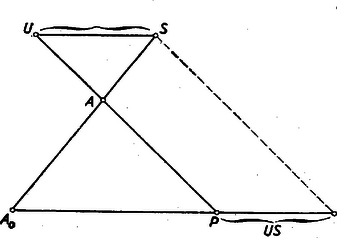AB és CD egy U pontban (4. ábra).
 
 
4. ábra
 

US az A0B0S és C0D0S síkok metszésvonalán van, ez pedig párhuzamos a két síkban húzható, egymással párhuzamos egyenesekkel, így az A0B0 és a C0D0 egyenesekkel. Messe az AB az A0B0-t P-ben, CD pedig C0D0-t Q-ban. Az eredeti gúla oldaléleinek közös hosszát jelöljük e-vel. Ekkor az UP-vel elmetszett US, A0P, és SA0 egyenesekből álló alakzatból adódik, hogy (5. ábra)
eSA=A0P+USUS.

 
5. ábra
 

(Ez közvetlenül világossá válik, ha S-ből párhuzamost húzunk UP-vel.) Hasonlóan nyerjük, hogy
eSB=B0P+USUS,eSC=C0Q+USUS,eSD=D0Q+USUS


Innen
e(1SA+1SC)=A0P+C0Q+2USUS,e(1SB+1SD)=B0P+D0Q+2USUS.
A0P és C0Q az A0PQC0 trapéz párhuzamos oldalai, B0P és D0Q pedig a B0PQD0 trapéz párhuzamos oldalai, így összegük a megfelelő trapéz középvonalának kétszerese. A0C0 és B0D0 azonban egy parallelogramma átlói, s így M0 metszéspontjuk mindkettőt felezi. Messe az M0-ből A0B0-vel húzott párhuzamos PQ-t az N pontban, akkor tehát M0N a két trapéz közös középvonala, és így
e(1SA+1SC)=2(M0N+US)US=e(1SB+1SD),
amiből a bizonyítandó állítás (e-vel osztva) már következik.
 

Megjegyzések: 1. A bizonyításban hallgatólag feltettük, hogy a PQ egyenes nem metszi a gúla alapsokszögét, tehát az A, B, C, D pontok egyike sem esik a megfelelő él meghosszabbítására. Ez azonban nem lényeges megszorítás, mert az alapsíkot önmagával párhuzamosan eltolhatjuk addig, míg az összes metszéspontok az alapnégyszögön kívül esnek. Ezzel a metszősík által az élekből lemetszett szakaszok nem változnak, és így a fenti fennálló összefüggések sem. (Egyébként a bizonyítás változtatás nélkül érvényes erre az esetre is, ha az US-sel párhuzamos szakaszokat pozitívnak vagy negatívnak tekintjük, amint irányuk a csúcsok felírt sorrendje szerint megegyezik vagy ellentétes US irányával.)
 

2. A bizonyításban csak egy helyen használtunk fel az alapról annál többet, hogy parallelogramma: mikor arra következtettünk, hogy a gúla oldalélei egyenlő hosszúságúak. Ha tetszés szerinti parallelogrammát megengedünk alapnak és a gúla csúcsa az átlók metszéspontjában az alapra emelt merőlegesen van, akkor is igaz annyi, hogy SA0=SC0 (jelöljük hosszukat e-vel) és SB0=SD0(=f). Ebben az esetben tehát a fenti levezetés annyit ad, hogy
e(1SA+1SC)=f(1SB+1SD),
vagyis egy paralelogramma alapú gúlát, amelynek csúcsa az átlók metszéspontjában emelt merőlegesen van, egy síkkal elmetszve, a szemközti élekből lemetszett szakaszok reciprok értékének összege fordított arányban áll egymással, mint a megfelelő élpárok hossza:
(1SA+1SC):(1SB+1SD)=f:e

3. Legyenek az 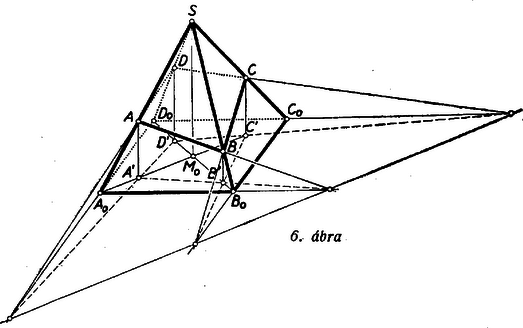A, B, C, D pontok merőleges vetületei az alaplapon A', B', C', D'. Ezek rendre az M0A0, M0B0, M0C0, M0D0 félegyenesre esnek, ahol M0 az alapnégyszög átlóinak metszéspontja (6. ábra).
 
 

Az A0B0, AB, A'B' egy ponton mennek keresztül. Megkeresve a B0C0, C0D0 és D0A0-n a megfelelő metszéspontokat, ezek egy egyenesen, a metszősík és az alapsík metszésvonalán sorakoznak. Könnyen látható, hogy az M0 pontból a vesszős pontokig terjedő szakaszok közt is fennáll egy olyan összefüggés, amilyen a feladatban szerepel. (Erre vonatkozólag az olvasó a jövő számunkban talál egy kitűzött feladatot.)
1)A feladat az előbbi szövegezésben szerepelt 407. feladatként. Két megoldás található a IV. kötet 4‐5. (1952. májusi) számában a 134‐135. oldalon.
A második formában a feladat lényegében benne foglaltatik a 706. feladatban, amelynek megoldását lásd a XII. kötet 4. (1956. április) számában a 110‐112. oldalon.

2)Kürschák J.: Matematikai Versenytételek I. rész. 2. kiadás. 77‐78. old.