|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Leonhard Euler (1707‐1783)
Euler Leonard a matematika egyik fejedelmének nevét minden olvasónk ismeri. Az idén van születésének kétszázötvenedik évfordulója. Ez igen nagy idő, mégis az évfordulóról az egész civilizált világon megemlékeznek, ami világosan mutatja Euler nagy jelentőségét a matematika történetében, sőt jelenére kiható kimagasló fontosságát. (Rendkívüli nagysága indokolja, hogy lapunk is megemlékezzék az évfordulóról.)
Euler 1707. április 15-én született egy Basel melletti kis faluban, ahol atyja kálvinista lelkész volt, aki fiát is papnak szánta. A baseli egyetem, ahova Euler került, volt akkor a matematikában a világ legnevezetesebb egyeteme, ahová messze földről gyülekeztek a tehetséges tanítványok, magyarok is. Tanáruk a világhírű Bernoulli (ejtsd: bernujji) János nagy matematikus és lelkes tanár, akinek két fia akkor szintén az egyetem hallgatója volt. Euler meleg barátságot kötött velük. Az ifjú Euler tehát nem lett pap, hanem azt az utat követte, amelyet tehetsége számára kijelölt. Matematikus lett. Az ifjú Bernoulli rábeszélésére 20 éves korában Pétervárra, a mai Leningrádba ment, ahol a Tudományos Akadémia főtitkára lett. 1741-ben II. Frigyes porosz király meghívására a berlini Tudományos Akadémiához került, de 25 év múlva visszament Pétervárra, ahol haláláig maradt. Fiatalon, 28 éves korában, elvesztette egyik szemét, 64 éves kora, 1771 óta, teljesen vak. Tudományos munkásságát mégsem hagyta abba. Egyik inasának, aki azelőtt szabólegény volt, tollba mondotta híres Algebráját, amely nemcsak a mai középiskolai anyagot tartalmazza, hanem jóval többet. A könyv annyira világos és oly könnyen érthető, hogy belőle a szabólegény alaposan megtanulta az algebra elemeit, úgy, hogy Euler diktálása alapján le tudta írni Euler gondolatait. Euler matematikai irodalmi tevékenysége tehát vaksága alatt sem szűnt meg, sőt talán még bővebben ömlött. A könyvet ma is nagyon ajánljuk németül vagy franciául tudó olvasóinknak.
Euler, ámbár a kor legnevezetesebb uralkodóinak udvartartásában élt, értéke tudatában sohasem süllyedt udvaronccá, mindig megmaradt büszke svájci polgárnak. II. Katalin cárnőnél ‐ aki maga is jelentékeny személyiség ‐ egy tábornok szóvá tette, miért Euler, a civil az Akadémia elnöke és nem ő, a tábornok. A cárnő azt felelte: ,,Tábornok, Bátyuskám, mindenki lehet, akit ÉN annak kinevezek, de Eulerré még én sem nevezhetek ki senkit.''
Euler a legtermékenyebb matematikus. Nyomtatott munkáinak száma , köztük több remek vastag kötet. Munkássága a matematika minden ágában korszakalkotó. Egyetlen más matematikus sem volt oly sokoldalú, mint ő, joggal elmondható, hogy egész más matematikát hagyott hátra, mint aminőt talált. A legfelsőbb matematikában messze kitolta tudásunk határait, de a legelemibb kérdésekbe is döntően szólt bele. Az iskolai matematika mai egyszerű alakja Eulernek köszönhető. Ha bárki ma háromszögről beszél, általában csúcsait , , -vel, szembenfekvő oldalait , , -vel jelöli. Ez a természetes és áttekinthető jelölési mód Eulertől ered. A , , , jelölések is Eulertől valók. Az , , jelöléseket is Euler vezette be. A 16. századbeli Rhaticus a derékszögű háromszög meghatározását adatból fólió oldalon tárgyalja, az az oly egyszerű mód, amelyet ma a II. osztályban tanultok, Eulertől ered. Általában a trigonometria mai oly könnyű alakja Eulertől származik, a goniometria majdnem minden formuláját Euler vezette le, a gömbháromszögtan (ez ma nem iskolai anyag, de mindenkinek szüksége van rá, aki pl. csillagászattal foglalkozik) is mai alakját Eulertől nyerte, legtöbb formuláját Eulernek köszöni. A trigonometriai függvényeket dimenzió nélküli számértékeknek fogja fel, és a körön mind a négy síknegyedben ábrázolja, az előjeleket az egyes negyedekben először Euler állapítja meg helyesen. Az analitikus geometria feltalálói a 17. századbeli Fermat (ejtsd: fermá) és Descartes (ejtsd: dékárt, az á rövid) csak egy tengelyt és a kezdőpontot használják, az ordinátatengelyt Euler vezette be.
Kötetekre lenne szükség, ha Eulernek csak legfőbb eredményeiről be akarnánk számolni, hiszen dolgozatának legtöbbje fontos és érdekes kérdésekre ad választ, gyakran többre is. Éppen azért csak néhány egyszerűen elérhető oly eredményének bemutatására szorítkozom, amelyek ifjú olvasóinkat érdekelhetik. A logaritmusnak mint a hatvány megfordításának, így tehát . alapművelet gyanánt való felfogása Eulertől származik. A 18. század elejének tudósai sokat vitatkoztak arról, mit kell a negatív szám logaritmusán érteni? A vitát Euler döntötte el, amikor megmutatta, hogy a logaritmus fogalmát célszerűen át lehet vinni a komplex számok körére is, de itt már a logaritmus végtelen sok értékű függvény, és a negatív szám logaritmusa komplex szám.
A háromszög Euler-féle egyeneséről az iskolában tanultatok. A háromszög magassági pontja , súlypontja , és a körülírt kör középpontja ebben a sorrendben egy egyenesen, az Euler-féle egyenesen fekszik, és . Az affinitás geometriai rokonságát is Euler vezette be. A Feuerbach-féle kört a francia szerzők Euler-féle körnek nevezik, mert ő ismerte fel először, hogy a háromszög oldalfelező pontjai, a magasságok talppontjai és a magasságok felső részeinek felezőpontjai ugyanazon körön feküsznek. (A Feuerbach-kör elnevezés mégis jogos, mert az a tétel, hogy a Feuerbach-kör érinti a háromszög mind a négy érintő körét, Feuerbachtól származik.)
,,Euler poliéder tétele'' is iskolai anyag. Ez a tétel tulajdonképp régibb, már Descartes leveleiben is előfordul, de Euler önállóan fedezte fel, Descartes levelét ugyanis csak 80 évvel Euler halála után publikálták. Ez a tétel úgy szól, ha egy szögletes test lapjainak száma , csúcsainak száma , és éleinek száma , akkor általában .
Mint ismeretes, ez az összefüggés konvex szögletes testekre mindig igaz, de konkáv egyenes vonalú testekre nem mindig áll fenn. Pl., ha a hasábhoz síklapokból álló fogantyút ragasztunk, a keletkezett testre (1. ábra) már nem áll a tétel. 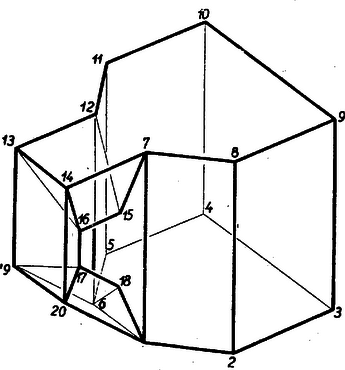 1. ábra
(Ábránkon , és , tehát ,) Újabban felteszik, hogy már az ógörög Archimedes is ismerte a poliéder tételt.
Most néhány, az iskola anyagában nem szereplő elemi természetű eredményét vagy bizonyítását fogom bemutatni.
Képzeljünk egy mezejű sakktáblát. Az Euler-féle ,, tiszt problémája'' a következő: ezredbeli különböző rendfokozatú tiszt helyezkedjék el úgy, hogy az ugyanazon sorban vagy oszlopban elhelyezkedő tisztek között ne legyen két azonos ezredbeli vagy azonos rendfokozatú. Euler ‐ ennél általánosabban ‐ kimutatta, hogy ez lehetetlen, ha különböző ezredbeli, számú különböző rendfokozatú tisztet akarnánk így elhelyezni.
Egy másik ily egyszerű Euler-féle probléma a ,,Königsbergi hidak'' problémája. Königsberg városát átszelő Pregel folyón átvezető hét híd helyzetét vázlatosan a 2. ábra mutatja. 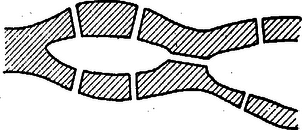 2. ábra
A feladat, hogy kell a sétát berendezni, ha valamennyi hídon át akarunk menni, de mindegyiken csak egyszer, hogy kiinduló pontunkra visszatérjünk. Ha a kérdést a budapesti hidakra vonatkozólag akarnám feltenni, azonnal láthatnók, hogy a feltétel teljesíthetetlen, mert a Margitszigetre vezető mind a két híd három ágú, tehát sétánknál egy ág vagy kimarad, vagy kétszer kell útba ejteni. A königsbergi hidakhoz visszatérve, hasonlóképpen nézzük azokat a területeket, amelyekre három híd vezet, pl. a folyó deltáját jobb oldalt. Nyilván csak két eshetőség lehetséges, ha mindhárom hidat útba akarjuk ejteni, vagy kétszer bemegyünk a deltába, és egyszer távozunk, vagy fordítva egyszer be, kétszer ki. A második esetben a séta a deltában kezdődött, különben nem távozhatnánk kétszer a deltából, ahová csak egyszer mentünk be, az első esetben hasonló okból a séta a deltában végződik. Amit a deltáról mondtunk, áll a folyó két pontjáról is, mert oda is három híd vezet, ahol tehát a sétának kezdődnie vagy végződnie kell. Ezek szerint (mint az ábra is mutatja) három oly terület van, ahol a sétának kezdődnie vagy végződnie kellene. Márpedig ez lehetetlen, a feladat tehát nem teljesíthető. Ez a probléma ugyebár játéknak, afféle matematikai mulatságnak tetszik, a valóságban azonban elvezet a mai matematika egyik fontos ágához, a topológiához.
A megokolás ugyan csak felsőbb matematikai meggondolásokkal lehetséges, de az eredmény egyszerű alakja és az iskola anyagával való összefüggése miatt bizonyítás nélkül megemlítem Euler fontos eredményeit az exponenciális és trigonometrikus függvények összefüggéséről. Az Euler-féle formula (, , a természetes logaritmus alapszáma) a legnagyobb matematikai felfedezések egyike. -re való alkalmazása adja az | |
ún. Moivre-féle formulát, amelynek ez az egyszerű, ma használt alakja Eulertől való, és amely sok trigonometriai felfedezésének nyitja. Ugyaninnen erednek a logaritmusra vonatkozó már említett felfedezései. Alkalmazásként zárt alakban fogjuk írni a fenti összefüggés segítségével az és a összegeket a hányadosú
mértani sorban. Az első összeg a valós (-t nem tartalmazó) rész, a második pedig a képzetes rész ( szorzója). Ha , azaz , akkor a mértani sort összegezve (és -nel bővítve)
[Az utolsó lépésben -vel bővítettünk, és felhasználtuk, hogy ]. Összehasonlítva két alakját, azt kapjuk, hogy
A kapott összefüggések könnyen igazolhatók komplex számok használata nélkül teljes indukcióval, vagy a bal oldalakat -lel szorozva, és a trigonometrikus szorzatokat különbséggé alakítva.
Áttérek Euler néhány számelméleti felfedezésének ismertetésére. Számelmélet-nek a matematika azon ágát nevezik, amely elsősorban az egész számok sajátságainak felderítésével foglalkozik. Száz évvel Euler előtt is élt már egy nagy matematikus, a már említett Fermat, aki fontos eredményeket ért el a számelméletben; de Fermat csak tételeit közölte, a módszert, amellyel eredményeihez jutott, elhallgatta. Euler életcéljának tekintette, hogy Fermat bizonyítás nélkül fennmaradt tételeire bizonyítást keressen. Ez a legtöbb esetben sikerült is neki, sőt sokszor lényegesen általánosította Fermat tételeit. Néhány ilyen vizsgálatáról beszámolok.
Ezek között a legnevezetesebb az, melyet ma röviden ,,Fermat tételé"-nek vagy ,,Fermat kis tételé"-nek neveznek. (,,Kis tételnek nevezett nagy tétel'' ‐ mondja szellemesen egy magyar matematikus.)
Először Euler bizonyította be, három bizonyítást adott rá, szépségük és érdekességük miatt mindhármat bemutatom. Maga a tétel így szól:
Legyen valamely tetszőleges prímszám, és nem osztható -vel, akkor osztható -vel vagy mai nyelven a kongruencia jelével
Az állítás -re magától értetődő, így a bizonyításban elég páratlan prímszámokra szorítkozni.
Euler első bizonyítása azt adja, hogy minden -ra osztható -vel. A bizonyítás a binomiális együtthatók egy egyszerű sajátságát használja fel és teljes indukcióval történik.
Ha , , , akkor a binomiális együttható (amelyről tudjuk, hogy egész szám) osztható -vel, mert a számláló osztható vele, viszont a nevező -nél kisebb számok szorzata, és így nem lehet -vel osztható, hiszen törzsszám.
A binomiális tétel értelmében | |
tehát | |
azaz osztható -vel. A tétel -re tehát helyes.
Tegyük most fel, hogy valamilyen értékre már tudjuk az állítás helyességét: Ekkor belátjuk, hogy helyes helyett -re is.
Az első zárójelben levő kifejezésről az indukciós feltevésből, a másodikról pedig a binomiális együttható fent belátott tulajdonságából tudjuk, hogy osztható -vel.
Ezzel igazoltuk a fent kimondott tételt. Ha osztható -vel, akkor mind a két tag külön osztható -vel. Ha nem osztható -vel, akkor ‐ prímszám lévén ‐ csak úgy lehet -vel osztható, ha a második tényező osztható vele, vagyis Ezzel igazoltuk az állítást eredeti alakjában is.
Második bizonyításában Euler a tételt általánosítja, mert kimutatja, hogy a tétel úgy fogalmazható, hogy összetett modulusokra is érvényes. A -nél kisebb, hozzá relatív prímszámok száma , amint Euler megmutatta, ez a Fermat-féle kongruenciában a kitevő jelentősége. Ha tehát egy tetszőleges egész szám ( lehet tehát prímszám és lehet összetett), akkor, ha a nála kisebb és hozzá relatív prím pozitív egész számok számát, amint szokás -nel jelöljük, ha a valamely -hez relatív prímszám, akkor a Fermat-féle kongruencia Euler-féle általánosítása.
Írjunk a rövidség kedvéért -t. Legyenek az -nél kisebb -hez relatív prímszámok (valamilyen sorrendben) Azt állítjuk, hogyha és egymáshoz relatív prímek, akkor az számokat -vel osztva, azok , maradékai újra az számok valamilyen sorrendben.
A maradék jelentése szerint osztható -nel . Itt is relatív prím -hez, mert különben és legnagyobb közös osztója lenne -nek is, de ez nem lehet, mert és relatív prím -hez, és így a szorzatuk is az.
Az számok tehát minden esetre az számok közül kerülnek ki. Mivel mind a két sorozatnak ugyanannyi eleme van, így annak megmutatásához, hogy az előbbiben szerepel az utóbbi minden eleme, elég megmutatni, hogy az előbbi sorozat különböző indexekhez tartozó elemei nem lehetnek egyenlők. Valóban, ha volna , vagyis és ugyanazt a maradékot adná -nel osztva, akkor osztható volna -nel. Mivel és relatív prímek, így ez csak úgy lehetne, ha osztható volna -nel. Ez azonban lehetetlen, mert és különböző, -nél kisebb pozitív számok, s így különbségük abszolút értéke -nél kisebb, és nem .
Ezzel igazoltuk a fent kimondott állításunkat. A maradékokra a kongruencia jelét használva, fennáll:
Szorozzuk össze ezt az kongruenciát: | |
de az -ek sorozata azonos (más sorrendben) az -k sorozatával, tehát szorzataik azonosak. Az -ek s az -k is egyenként relatív prímek -hez, tehát szorzatuk is az, ezért ezzel a szorzattal a kongruencia mindkét oldalán egyszerűsíthetünk, s marad vagy helyébe az értékét beírva
Euler harmadik bizonyítása is közvetlenül ezt az utóbbi kongruenciát bizonyítja, sőt még több derül ki belőle. Azt mutatja meg ugyanis, hogyha a legkisebb kitevő, amelyre az kongruencia teljesül, akkor osztója -nek.
Tekintsük ugyanis -nak egymás után következő hatványait: Ezeknek az osztóra vett maradékai csak véges sok értéket vehetnek fel (legfeljebb -et), így elég messze menve a sorozatban található két hatvány és , amely ugyanazt a maradékot adja, vagyis amelyek különbsége osztható -nel. De , s így is relatív prím -hez, pedig osztható -nel, tehát is osztható -nel. Van tehát olyan kitevő (pl. ), amelyre osztható -nel, vagy a kongruenciák nyelvén
Legyen a legkisebb kitevő, melyre az kongruencia teljesül. Most lehetséges, hogy az (1) sorozat kimeríti az összes -nál kisebb és -hoz relatív prímszámokat. Ekkor , és így az állítás bizonyítást nyert. Ha nem, akkor van olyan -hez relatív prím szám, amelynek az osztóra vett maradéka különbözik az sorozat minden elemének maradékától. Szorozzuk meg az (1') sorozat minden tagját -vel, így kapjuk az sorozatot, amelyben nincs két egymással kongruens szám, és amelynek minden tagja különbözik az (1') sorozat minden tagjától. Valóban, ha valamilyen kitevőkre lenne, akkor lenne, és itt , holott a legkisebb pozitív kitevő, amelyre a kongruencia teljesül.
Ha pedig lenne, akkor volna, azaz maradéka előfordulna az (1') sorozat maradékai közt, holott ennek az ellenkezőjét tettük fel.
Ha az (1') és (2) sorozatok együtt sem merítenék ki az -nél kisebb és hozzá relatív prímszámok sorát, akkor volna oly szám, mely maradéka egyik sorozat maradékai közt sem foglaltatnék, és ugyanúgy kimutathatnók, hogy az sorozat mindenikének maradéka különböző, és az (1') és (2) sorozat bármely tagjáétól is különbözik, és így tovább, a különböző maradékok száma mindenesetre, osztható -val. Q. e. d.
Ez a bizonyítás ‐ amint Speiser baseli professzor matematikai antológiájában mondja, a 18. század egyik alapvető teljesítménye. Vele kezdődik ‐ amint ugyancsak Speiser mondja ‐ a matematikában az elegancia, mert a számolás elkerülésével vezet nagy jelentőségű eredményhez. A bizonyításban a matematika egy fontos új ágának az alapgondolata rejlik, mely a mai matematikában uralkodó. Nem csoda tehát, hogy minden matematikai antológiának nélkülözhetetlen alkatrésze ez a csodálatos bizonyítás.
Euler további számelméleti felfedezéseinek felsorolásában is felhasználom a kongruencia fogalmát, mert így rövidebben mondhatom el őket.
Euler igen sokat foglalkozott a kvadratikus kongruenciákkal. Ezalatt ezt értjük: Legyen oly egész szám, mely nem osztható a törzsszámmal. Akkor az kongruencia megoldható, ha és megoldhatatlan (azaz nincs oly szám; melynek négyzetéből -t kivonva, -vel osztható számot kapunk), ha Rögtön látni, hogy ebből az ,,Euler-féle kritériumból'' a Fermat-tétel újabb ‐ negyedik ‐ bizonyítása következik, mert négyzetre emelés minden esetben kongruenciát szolgáltatja.
A kvadratikus kongruenciákkal való állandó foglalkozásának eredményeit összefoglalva élete utolsó évében egy igen nagy jelentőségű tételt talált, az elemi számelmélet egyik legmélyebb tételét. Legyen és két prímszám. Ha és valamelyike alakú, akkor az és kongruenciáknak vagy mindkettője megoldható vagy egyikük sem; ha pedig is, is alakú, akkor a két kongruencia közül mindig megoldható az egyik, de csak az egyik. A két kongruencia fennállása, ill. lehetetlensége között összefüggést talált, azért a tételt ma reciprocitási tételnek nevezik. Tételét Euler nem tudta bebizonyítani, ez csak jóval később a 19 éves Gaussnak sikerült, aki Eulertől függetlenül szintén felfedezte.
Mondtam már, hogy Euler életproblémájának tekintette Fermat bizonyítás nélkül fennmaradt tételeinek bebizonyítását. Ezek közül néhányat felsorolok.
Minden alakú prímszám két négyzetszám összege.
Minden természetes egész szám előállítható, mint négyzetszám összege. Ezen tétel bizonyítási kísérletei közben találta a következő csodálatos azonosságot:
(bizonyítását az olvasóra bízom), melynek folytán elég a tételt prímszámokra bizonyítani.
A diofantoszi egyenletek elmélete is igen nagy eredményeket köszönhet Euler-nek. Említett algebrai könyvének második része a diofantoszi egyenletekkel foglalkozik. Bebizonyította, hogy az egyenlet egyetlen megoldása , , és az egyenletnek csak két megoldása van , és , . Fermat ezekre a tételeire igen büszke volt, de csak Euler bizonyítása maradt fenn. Bebizonyította továbbá az ún. Fermat-féle sejtés következő speciális eseteit, hogy az egyenletek -tól különböző egész számokban lehetetlenek. Felemlítem továbbá a következő (Fermat-tól független) eredményét. Az határozatlan egyenlet összes megoldásai , , ; , , , vagyis két egymásra következő szám közül ‐ a ; ; pároktól eltekintve ‐ nem lehet az egyik köb, a másik négyzet.
Lapunkban egyik régebbi cikkemben ismertettem a biztosítási matematika elemeit. A biztosítási matematika is Eulertől származik.
Euler főérdeme a felsőbb matematika részletes kidolgozása, hogy a természet vizsgálatára alkalmas legyen. Minderről a sok bámulatos eredményről nem szólhattam, de egyik könnyen érthető, ámbár igen magas segédeszközöket igénylő problémájáról megemlékezem egy-két szóval. Keresendők azon görbék, amelyek valamely kívánt sajátsággal a legnagyobb vagy a legkisebb mértékben rendelkeznek. Pl. az egyenlő kerületű zárt görbék közül melyeknek a területe a legnagyobb.
Nem hagyom szó nélkül, hogy akadtak matematikusok, akik kifogásolták, hogy Euler a matematika filozófiai alapjait elhanyagolta, és csak a matematikával (és alkalmazásaival) törődött, ebben pedig a legnagyobb mesterek közé tartozik, a logikai alapokkal szemben pedig közömbös. Ezért egy-két eredménye hibás, de egyébként csodálatos matematikai érzéke megóvta azoktól a hibáktól, amelyekre a régi idők nem elég precíz fogalomalkotása több kortársát csábította. A nagy alkotó korszakokban visszaszorul a kritika, amely meddőbb korszakokban virul. Euler pedig a legnagyobb stílusú alkotók közül való. Csak igen kevés alkotását soroltam fel ‐ és mégis micsoda gazdagság!
A matematikának nagyon sok kedvelője van napjainkban, különösen hazánkban. Ezeket fogva tartja a matematika szépségének varázsa. Már pedig Euler levezetései ‐ amint a bemutatott ízelítők is ‐ a bennük rejlő szépség folytán sok-sok nemzedéknek okoztak gyönyörűséget, és a ,,mathematica delectans'' nagy művészének megszerezték sok-sok ezer olvasójának bámulatát és tiszteletét. A magyar ifjúság is örömmel hódol a zseniális matematikus emlékének.
A Bernoulli család nevezetes a tudomány történetében, mert benne jóval 100 éven túl, több nemzedéken át öröklődött a kivételes matematikai tehetség.A kongruencia fogalmát és műveleti szabályát ismertettem lapunk idei évfolyamában: K. M. L. XIV, 1957. 34. és 35. o., ismeretüket tehát feltételezem. Lásd még Faragó László: A számelmélet elemei, 48‐57. o. vagy Matematikai Versenytételek I. rész, 45‐47. o.Lásd K. M. L. XIV., 1957. 67. o., vagy Faragó L,: A számelmélet elemel 42,‐44. o.A. Speiser: Klassische Stücke der Mathematik, Zarich und Leipzig 1925. Orell Fössli
110. o.Lásd K. M. L. X. kötet, 1955. ápr. 98. o.Lásd K. M. L. IX., 1954. nov. 68‐70. o. |
 PDF | MathML
PDF | MathML