Kezdőlap


Cím:	A determinánsokról (1. közlemény)
Szerző(k):	Scharnitzky Viktor
Füzet:	1957/október, 33 - 41. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A kétismeretlenes elsőfokú egyenletrendszer
megoldása, a másodrendű determináns

1. közlemény

A másodfokú egyenlet úgynevezett gyökképletének levezetésekor az a meggondolás vezet bennünket, hogy felesleges dolog a másodfokú egyenlet megoldását kezünkbe adó módszert (tudniillik a ,,teljes négyzetté való kiegészítés'' módszerét) minden egyes adott másodfokú egyenlet esetében újra és újra végigcsinálnunk; sok időt és fáradságot takarítunk meg azzal, hogy egyszer s mindenkorra megoldjuk az

a x^{2} + b x + c = 0

általános másodfokú egyenletet. Adott esetben azután csak be kell helyettesítenünk az

a

b

c

együtthatók számértékét az így nyert gyökképletbe.
A kétismeretlenes elsőfokú (idegen szóval: lineáris) egyenletrendszer megoldására is levezethetünk egy ilyen általános képletet, amelynek hasonló gyakorlati haszna van olyankor, ha gyakran kell ilyen egyenletrendszert megoldanunk.
Induljunk ki a kétismeretlenes elsőfokú egyenletrendszer

\begin{matrix} A_{1} x + B_{1} y = C_{1} & (1) \\ A_{2} x + B_{2} y = C_{2} \end{matrix}

általános alakjából.
Az (1) egyenletrendszer megoldására alkalmazzuk pl. az ,,egyenlő együtthatók'' módszerét. Evégből szorozzuk meg az első egyenletet

B_{2}

-vel, a második egyenletet

- B_{1}

-el és adjuk össze őket, majd az elsőt

- A_{2}

-vel szorozzuk és a másodikat

A_{1}

-el, és ugyancsak összeadjuk őket. Így az

\begin{matrix} (A_{1} B_{2} - B_{1} A_{2}) x = C_{1} B_{2} - B_{1} C_{2}, \\ (A_{1} B_{2} - B_{1} A_{2}) y = A_{1} C_{2} - C_{1} A_{2} \end{matrix}

egyismeretlenes egyenletekhez jutunk. Azonnal látszik, hogy a jobb oldali kifejezések a bal oldali együtthatókból úgy keletkeztek, hogy annak az ismeretlennek az együtthatói helyébe, amelyiket kiakarunk fejezni, a jobb oldali adott értékeket írjuk. Célszerű az ilyen típusú szorzatkülönbség jelölésére új jelet bevezetni. Ez a szorzatkülönbség egy négyváltozós függvény, mivel azonban az egyenletrendszer felírásában bizonyos helyeken levő együtthatókat kell egymás helyére írni, ezért célszerű lesz a változókat nem egymás után írni, hanem táblázatosan úgy, ahogyan az egyenletrendszerben szerepelnek. A táblázatot két függőleges vonal közé zárjuk:

\begin{matrix} | \binom{r}{t} \binom{s}{u} | = r u - s t . \end{matrix}

A bal oldalon álló kifejezést másodrendű determinánsnak¹ nevezzük.
Az

r

s

t

u

mennyiségek a másodrendű determináns elemei. Az

r

és

s

alkotja a másodrendű determináns első sorát, a

t

és

u

a második sorát, hasonlóképpen az

r

és

t

, illetve az

s

és

u

alkotja a másodrendű determináns első, illetve második oszlopát.
A determináns értékének kiszámítását a következő szemléletes eljárás teszi könnyen megjegyezhetővé:

\begin{matrix} r s \\ ↘ / \\ ↙ \ \\ ↙ t u ↘ \\ - + \end{matrix}

A teljes vonallal kihúzott nyíl (főátló) két végénél álló számok szorzatából levonjuk a szaggatottan kihúzott nyíl (mellékátló) két végén álló számok szorzatát.
Az (1) egyenletrendszer bal oldalán álló együtthatókból alkotott

\begin{matrix} D = | \binom{A_{1}}{A_{2}} \binom{B_{1}}{B_{2}} | = A_{1} B_{2} - B_{1} A_{2} \end{matrix}

determinánst az egyenletrendszer determinánsának szokás nevezni. Tegyük fel, hogy

D \neq 0

, ekkor az egyenletrendszer megoldása csak a következő lehet:

\begin{matrix} x = \frac{D_{x}}{D} = \frac{| \binom{C_{1}}{C_{2}} \binom{B_{1}}{B_{2}} |}{| \binom{A_{1}}{A_{2}} \binom{B_{1}}{B_{2}} |}; y = \frac{D_{y}}{D} = \frac{| \binom{A_{1}}{A_{2}} \binom{C_{1}}{C_{2}} |}{| \binom{A_{1}}{A_{2}} \binom{B_{1}}{B_{2}} |} . \end{matrix}

A számlálóban álló

x

(ill.

y

) index azt jelöli, hogy a

D_{x}

(ill.

D_{y}

) determináns a

D

determinánshól úgy keletkezett, hogy az

x

(ill.

y

) együtthatói helyett írtuk be az egyenletek jobb oldalán álló számokat.
Behelyettesítéssel könnyen meggyőződhetünk arról, hogy az így kapott értékek valóban megoldásai az (1) egyenletrendszernek.
(Könnyű belátni még azt is, hogyha az egyenletrendszer determinánsa 0, de

D_{x}

és

D_{y}

valamelyike nem ‐ és ekkor a másik sem ‐, akkor a rendszer ellentmondó, ha pedig mindhárom determináns értéke 0, akkor a két egyenlet csak egy állandó szorzóban különbözik.)
A kétismeretlenes (és amint azt a későbbiekben látni fogjuk: a többismeretlenes) egyenletrendszer megoldásának ezt a módját Cramer-szabálynak szokás nevezni.
Gyakorlásul oldjuk meg a Cramer-szabály segítségével a következő egyenletrendszert:

\begin{matrix} 3 x - 5 y & = 13, \\ 5 x - 7 y & = 19. \end{matrix}

Mivel az egyenletrendszer determinánsa

\begin{matrix} D = | \binom{3}{5} \binom{- 5}{- 7} | = 3 \cdot (- 7) - (- 5) 5 = 4, \end{matrix}

azaz nem nulla,

\begin{matrix} x & = \frac{| \binom{13}{19} \binom{- 5}{- 7} |}{| \binom{3}{5} \binom{- 5}{- 7} |} = \frac{4}{4} = 1, \\ y & = \frac{| \binom{3}{5} \binom{13}{19} |}{| \binom{3}{5} \binom{- 5}{- 7} |} = \frac{- 8}{4} = - 2. \end{matrix}

II. A háromismeretlenes elsőfokú egyenletrendszer megoldása,
a másodrendű determináns tulajdonságai, a harmadrendű determináns

1. A másodrendű determináns fogalmának segítségével rátérhetünk a háromismeretlenes egyenletrendszer megoldására is.
Az egyenletrendszerben szereplő együtthatókat külünböző betűk helyett ‐ az áttekinthetőség kedvéért ‐ egy betűvel és kettős indexszel jelöljük. Az első index jelöli az egyenlet sorszámát, a második index az ismeretlen sorszámát.
Tekintsük az

\begin{matrix} a_{11} x + a_{12} y + a_{13} z & = b_{1} \\ a_{21} x + a_{22} y + a_{23} z & = b_{2} & (2) \\ a_{31} x + a_{32} y + a_{33} z & = b_{3} \end{matrix}

egyenletrendszert.
Foglalkozzunk először csak a (2) egyenletrendszer két utolsó egyenletével, gondoljuk

z

-t közelebbről meg nem határozott, de adott mennyiségnek, éppen úgy, mint az együtthatókat, és utólag vizsgáljuk meg, hogyan kell

z

-t megválasztanunk ahhoz, hogy az első egyenlet is teljesüljön. Rendezzük át a két egyenletet:

\begin{matrix} a_{21} x + a_{22} y & = b_{2} - a_{23} z, \\ a_{31} x + a_{32} y & = b_{3} - a_{33} z . \end{matrix}

Ha a bal oldalon álló együtthatókból alkotott determináns értéke nem nulla, akkor az első pontban megismert módszer segítségével:

\begin{matrix} x = \frac{| \binom{b_{2}}{b_{3}} \binom{- a_{23} z}{- a_{33} z} \binom{a_{22}}{a_{32}} |}{| \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |}; y = \frac{| \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} \binom{- a_{23} z}{- a_{33} z} |}{| \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |} . \end{matrix}

Ezek minden

z

értékhez adnak egy-egy

x

és

y

értéket, de az így kapott

x

y

z

érték-rendszer általában nem elégíti ki az első egyenletet is. Ha azonban

x

és

y

kapott kifejezését behelyettesítjük az első egyenletbe,

z

-re kapunk egyenletet. Csak az ezt kielégítő

z

és a hozzátartozó

x

és

y

lehet a (2) egyenletrendszer megoldása. Behelyettesítés előtt azonban alakítsuk át

x

és

y

számlálóját úgy, hogy a

z

-t tartalmazó tagok különválasztva szerepeljenek. Ez a másodrendű determináns néhány tulajdonságának felhasználásával könnyen elérhető.
Lássuk be tehát előbb a másodrendű determináns alábbi tulajdonságait:
a) A másodrendű determináns oszlopait egymással felcserélve a determináns előjele megváltozik.
Ugyanis az

\begin{matrix} | \binom{r}{t} \binom{s}{u} | és | \binom{s}{u} \binom{r}{t} | \end{matrix}

determinánsok értékét kiszámítva az

r u - t s

és

s t - u r

kifejezéseket kapják, amelyek csak előjelben különböznek egymástól.
A továbbiakban azért beszélhetünk ,,valamelyik'' oszlopról és nem kell ,,az első'' vagy ,,a második'' oszlopról beszélni, mert oszlopcserével elérhető, hogy bármelyik oszlop legyen az első.
b) Ha a másodrendű determináns egyik oszlopának minden elemét megszorozzuk egy számmal, a determináns értéke is szorzódik ezzel a számmal.
Bizonyítás:

\begin{matrix} | \binom{r}{t} \binom{c s}{c u} | = c r u - c t s = c (r u - t s) = c | \binom{r}{t} \binom{s}{u} | . \end{matrix}

c) Ha a másodrendű determináns valamelyik oszlopának minden eleme két szám összegére bontható, akkor a determináns két determináns összegére bontható a következő módon:

\begin{matrix} | \binom{r}{t} \binom{+ r'}{+ t'} \binom{s}{u} | = | \binom{r}{t} \binom{s}{u} | + | \binom{r'}{t'} \binom{s}{u} | . \end{matrix}

Számítsuk ki a két oldalon álló determinánsok értékét:

\begin{matrix} | \binom{r}{t} \binom{+ r'}{+ t'} \binom{s}{u} | = (r + r') u - (t + t') s = r u + r' u - t s - t' s, \\ | \binom{r}{t} \binom{s}{u} | + | \binom{r'}{t'} \binom{s}{u} | = r u - t s + r' u - t' s . \end{matrix}

Ez a két érték pedig valóban egyenlő.
d) A másodrendű determináns értéke nem változik, ha sorait felcseréljük oszlopaival (,,tükrözzük a determinánst a főátlóra''):

\begin{matrix} D = | \binom{r}{t} \binom{s}{u} | = | \binom{r}{s} \binom{t}{u} | . \end{matrix}

Kiszámítva a két determináns értékét látjuk, hogy mindkettőnek értéke

r u - s t

.
Ez a tulajdonság biztosítja azt, hogy a másodrendű determináns oszlopaira bebizonyított tulajdonság vagy tétel automatikusan alkalmazható a másodrendű determináns soraira is. A sorok és oszlopok egyenrangúak.
Ezeket a tulajdonságokat felhasználva tehát alakítsuk át

x

és

y

számlálóját úgy, hogy a

z

-t tartalmazó tagok különválasztva szerepeljenek.
A c) tulajdonság alapján először felbontjuk a determinánst két determináns összegére, majd ─ hogy az együtthatók olyan sorrendben szerepeljenek, mint az egyenletrendszerben ‐ felcseréljük a kapott két determináns oszlopait (a) tulajdonság), végül a második determináns második oszlopából kiemeljük a

z

-t (b) tulajdonság):

\begin{matrix} | \binom{b_{2}}{b_{3}} \binom{- a_{23} z}{- a_{33} z} \binom{a_{22}}{a_{32}} | = | \binom{b_{2}}{b_{3}} \binom{a_{22}}{a_{32}} | + | \binom{- a_{23} z}{- a_{33} z} \binom{a_{22}}{a_{32}} | = - | \binom{a_{22}}{a_{32}} \binom{b_{2}}{b_{3}} | + z | \binom{a_{22}}{a_{32}} \binom{a_{23}}{a_{33}} | . \end{matrix}

Hasonló módon

\begin{matrix} | \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} \binom{- a_{23} z}{- a_{33} z} | = | \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} | + | \binom{a_{21}}{a_{31}} \binom{- a_{23} z}{- a_{33} z} | = | \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} | - z | \binom{a_{21}}{a_{31}} \binom{a_{23}}{a_{33}} | . \end{matrix}

x

és

y

kifejezése átalakítás után:

\begin{matrix} x = \frac{- | \binom{a_{22}}{a_{32}} \binom{b_{2}}{b_{3}} | + z | \binom{a_{22}}{a_{32}} \binom{a_{23}}{a_{33}} |}{| \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |}; y = \frac{| \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} | - z | \binom{a_{21}}{a_{31}} \binom{a_{23}}{a_{33}} |}{| \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |} . \end{matrix}

Ezt a két értéket az első egyenletbe helyettesítve és

\begin{matrix} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} | -vel végigszorozva mindkét oldalt kapjuk: \end{matrix}

\begin{matrix} a_{11} {- | \binom{a_{22}}{a_{32}} \binom{b_{2}}{b_{3}} | + z | \binom{a_{22}}{a_{32}} \binom{a_{23}}{a_{33}} |} + a_{12} {| \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} | - z | \binom{a_{21}}{a_{31}} \binom{a_{23}}{a_{32}} |} + a_{13} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} | z = b_{1} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |, \end{matrix}

vagy átrendezve:

\begin{matrix} {a_{11} | \binom{a_{22}}{a_{32}} \binom{a_{23}}{a_{33}} | - a_{12} | \binom{a_{21}}{a_{32}} \binom{a_{23}}{a_{33}} | + a_{13} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} |} z = a_{11} | \binom{a_{22}}{a_{32}} \binom{b_{2}}{b_{3}} | - a_{12} | \binom{a_{21}}{a_{31}} \binom{b_{2}}{b_{3}} | + b_{1} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} | . & (3) \end{matrix}

Vegyük észre, hogy a bal, illetve jobb oldalon álló másodrendű determinánsok között összefüggés áll fenn, bizonyos elemek (pl. az egymás alatt álló determinánsok első oszlopainak elemei) a helyükön maradtak, más elemek helyébe mások kerültek. Célszerű lesz

z

együtthatója számára, mely az egyenletrendszerben szereplő kilenc együttható függvénye új jelet bevezetni. Az elemeket ‐ akárcsak a másodrendű determináns jelölésénél ‐ itt is táblázatosan helyezzük el úgy, ahogyan az egyenletrendszerben szerepelnek:

\begin{matrix} | \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} | = a_{11} | \binom{a_{22}}{a_{32}} \binom{a_{23}}{a_{33}} | - a_{12} | \binom{a_{21}}{a_{31}} \binom{a_{23}}{a_{33}} | + a_{13} | \binom{a_{21}}{a_{31}} \binom{a_{22}}{a_{32}} | \end{matrix}

(4)

A bal oldalon szereplő három sorba és három oszlopba rendezett kilenc számból álló kifejezést harmadrendű determinánsnak nevezzük.
Az első index jelöli az elem sorát (sorindex), a második index jelöli az elem oszlopát (oszlopindex). Ezzel a jelölési módszerrel igen egyszerűen jelölhető meg egy-egy elem helye a determinánsban.
A harmadrendű determináns kiszámítását három másodrendű (tehát eggyel alacsonyabb rendű) determináns kiszámítására vezetjük vissza, melyek értékét már ki tudjuk számítani.
A (4) eljárást ‐ mivel az első sor elemeihez tartozó másodrendű determinánsok kiszámítására vezettük vissza a harmadrendű determináns kiszámítását ‐ harmadrendű determináns első sora szerinti kifejtésének szoktuk nevezni.
A harmadrendű determináns jelölésmódját felhasználva (3)-ból ‐ ha az egyenletrendszer determinánsa

\begin{matrix} D = | \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} | \neq 0, \\ z = \frac{D_{z}}{D} = \frac{| \begin{matrix} a_{11} & a_{12} & b_{1} \\ a_{21} & a_{22} & b_{2} \\ a_{31} & a_{32} & b_{3} \end{matrix} |}{| \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} |} . \end{matrix}

A számlálóban szereplő determináns az egyenletrendszer determinánsából ‐ mint ahogyan azt a kétismeretlenes egyenletrendszer megoldásánál már láttuk ‐ úgy keletkezik, hogy annak az ismeretlennek (

z

-nek) együtthatói helyébe, amelyiket ki akartunk fejezni, a jobb oldalon álló adott értékeket helyettesítettük.
Teljesen hasonló eljárással

x

-re és

y

-ra a következő kifejezéseket kapjuk:

\begin{matrix} x = \frac{D_{x}}{D} = \frac{| \begin{matrix} b_{1} & a_{12} & a_{13} \\ b_{2} & a_{22} & a_{23} \\ b_{3} & a_{32} & a_{33} \end{matrix} |}{| \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} |}; y = \frac{D_{y}}{D} = \frac{| \begin{matrix} a_{11} & b_{1} & a_{13} \\ a_{21} & b_{2} & a_{23} \\ a_{31} & b_{3} & a_{33} \end{matrix} |}{| \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} |} . \end{matrix}

A kapott értékeket behelyettesítve az egyenletrendsszerbe egyszerű, de hosszadalmas számolással belátható, hogy ezek valóban megoldásai a (2) egyenletrendszernek.
Gyakorlásul oldjuk meg a következő egyenletrendszert:

\begin{matrix} x - 2 y + z = 2, \\ 3 x + 8 y - 6 z = - 5, \\ 6 x + 10 y + 3 z = 4. \end{matrix}

Számítsuk ki először az egyenletrendszer determinánsát:

\begin{matrix} D = | \begin{matrix} 1 & - 2 & 1 \\ 3 & 8 & - 6 \\ 6 & 10 & 3 \end{matrix} | = 1 | \binom{8}{10} \binom{- 6}{3} | - (- 2) | \binom{3}{6} \binom{- 6}{3} | + 1 | \binom{3}{6} \binom{8}{10} | = \\ = 84 - (- 2) 45 + (- 18) = 156, \end{matrix}

tehát nem 0. Így

\begin{matrix} x & = \frac{D_{x}}{D} = \frac{| \begin{matrix} 2 & - 2 & 1 \\ - 5 & 8 & - 6 \\ 4 & 10 & 3 \end{matrix} |}{156} = \frac{104}{156} = \frac{2}{3}, \\ y & = \frac{D_{y}}{D} = \frac{| \begin{matrix} 1 & 2 & 1 \\ 3 & - 5 & - 6 \\ 6 & 4 & 3 \end{matrix} |}{156} = \frac{- 39}{156} = \frac{1}{4}, \\ z & = \frac{D_{z}}{D} = \frac{| \begin{matrix} 1 & - 2 & 2 \\ 3 & 8 & - 5 \\ 6 & 10 & 4 \end{matrix} |}{156} = \frac{130}{156} = \frac{5}{6} . \end{matrix}

2. Ha a (4) kifejtésben szereplő másodrendű determinánsok értékét kiszámítjuk, a harmadrendű determináns értékére a következő kifejezést kapjuk:

\begin{matrix} a_{11} a_{22} a_{33} - a_{11} a_{23} a_{32} - a_{12} a_{21} a_{33} + \\ + & a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} . \end{matrix}

A kifejezésben szereplő tagok kiszámításának módját a következőképpen jegyezhetjük meg könnyen: Egészítsük ki gondolatban a determinánst az első és második oszloppal: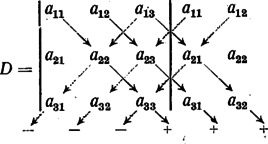

Vegyük észre, hogyha a kihúzott nyilak (főátlók) mentén levő elemek szorzatából levonjuk a szaggatott nyilak (mellékátlók) mentén levő elemek szorzatát (a sorrendtől eltekintve) éppen a harmadrendű determináns előbb kiszámított értékét kapjuk. Ez az eljárás a Sarrus-szabály néven ismeretes.
Számítsuk ki a Sarrus-szabály segítségével pl. az előző pontban szereplő

D_{x}

determináns értékét.

\begin{matrix} D_{x} = | \begin{matrix} 2 & - 2 & 1 \\ - 5 & 8 & - 6 \\ 4 & 10 & 3 \end{matrix} | \begin{matrix} 2 & - 2 \\ - 5 & 8 \\ 4 & 10 \end{matrix} = 48 + 48 - 50 - (32 - 120 + 30) = 104. \end{matrix}

A harmadrendű determináns értéke tehát bizonyos szorzatok: a determináns tagjainak összege. Vizsgáljuk meg tüzetesebben ezen szorzatokat, hogy a bennük mutatkozó szabályosságot felismerjük !
A szorzatokban a tényezőket olyan sorrendben írtuk már eleve, hogy az első indexek nagysága növekedjék. Észre kell vennünk azt, hogy minden szorzatban az első indexek éppen 1, 2, 3, ami azt jelenti, hogy minden szorzatban minden sorból egy és csak egy elem szerepel. Figyeljük meg most a második indexeket. Ezek 123, 132, 213, 231, 312, 321, azaz az 1, 2, 3 számok összes lehetséges sorrendben való elrendezése, összes permutációja. ²
Mivel az egyes tagokban a második indexek is mind különbözők, ezért a tagok minden tényezője más-más oszlopból való. Ezek szerint a harmadrendű determináns minden egyes tagja olyan három tényezőből álló szorzat, amely tényezők mind különböző sorokból és oszlopokból valók. Az a tény, hogy az oszlopindexek minden lehetséges permutációja szerepel egyszer és csakis egyszer (feltéve, hogy a sorindexek természetes sorrendben állnak), arra utal, hogy a determináns összes tagjait úgy kell elkészíteni, hogy minden lehetséges módon kiválasztunk a determinánsból három-három elemet ‐ de úgy, hogy köztük ne legyen két elem ugyanazon sorból, vagy ugyanazon oszlopból, ezeket összeszorozzuk és

+

vagy

-

előjellel látjuk el.
Nézzük meg most, milyen előjelet írunk a szorzatok elé:

\begin{matrix} Oszlopindex permutációk & 123 & 132 & 213 & 231 & 312 & 321 \\ Inverziók^{3}száma & 0 & 1 & 1 & 2 & 2 & 3 \\ A megfelelő szorzat előjele & + & - & - & + & + & - \end{matrix}

³

Azonnal láthatjuk, hogy a szorzat aszerint kap

+

vagy

-

előjelet, amint az oszlop indexe permutációjában szereplő inverziók száma, azaz maga a permutáció páros-e vagy páratlan.
Így

\begin{matrix} D = | \begin{matrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{matrix} | = \sum_{p}^{} {(- 1)}^{j} a_{1} k_{1} a_{2} k_{2} a_{3} k_{3}, \end{matrix}

ahol

k_{1}

k_{2}

k_{3}

, az 1, 2, 3 oszlopindexek egy permutációja,

j

ezen permutáció inverzióinak a száma, az összegezés pedig az 1, 2, 3 elemek minden lehetséges permutációjára (

p

) terjesztendő ki.

¹Az elsőfokú egyenletrendszerek megoldásánál fellépő sajátságos kifejezéseket először G. W. Leibniz (1646‐1716) német matematikus és filozófus vizsgálta rendszeresen.
A determinánsok első tudatos alkalmazója G. Cramer (1704‐1752) genfi matematikus.
A ,,determináns'' elnevezés C. F. Gauss (1777‐1855) német matematikustól ered.
A determináns mai jelölése A. Cayley (1821‐1895) angol matematikustól származik.

² $n$ db. elem egy permutációján az $n$ elem egy sorrendjét értjük. $n$ elem összes permutációinak száma $1 \cdot 2 \cdot 3 ... n = n$ ! KML; IV. kötet (1952) 37. oldal.

³Ha valamely permutációban egy a természetes sorrendben hátrább álló elem egy, a természetes sorrendben előbb állót megelőz, azt mondjuk, hogy e két elem inverziót alkot, vagy hogy inverzióban vannak. Pl. a 31254 permutációban a következő elempárok vannak inverzióban: 31, 32, 54.
Beszélhetünk egy permutáció inverzióinak számáról is, ez a szóban forgó permutáció inverzióban levő elempárjainak a száma. A 31254 permutáció inverzióinak száma három. Páros, ill. páratlan permutációnak nevezzük az olyan permutációt, amely inverzióinak száma páros, ill. páratlan. A 31254 permutáció páratlan.