Cím: Az 1957. évi Országos Matematikai Tanulmányi Verseny I. fordulója
Füzet: 1957/május, 134 - 141. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez idén a verseny I. fordulója a szokottnál valamivel későbben, március 20-án folyt le az egyes iskolákban a gimnáziumok és ipari technikumok III. és IV. osztályú tanulói részére változatlan feltételek mellett. Munkaidő 5 óra. Beadtak összesen 229 iskolában 3104 dolgozatot (tavaly 236 iskolában 3220 dolgozatot). A gimnáziumok száma tovább növekedett 179-ről. 184-re, viszont az ipari technikumok száma jelentékeny mértékben tovább csökkent 57-rő1 45-re.
A központi versenybizottság április 19-i javaslata alapján 122 iskola 325 tanulója ‐ a dolgozat-beadók 10,4%-a ‐ került a II. (döntő) fordulóba (tavaly 138/365 ‐ 11,3%). Részletes adatok iskolafajok, megyék és városok szerint az itt közölt táblázatban találhatók.
A döntőbe került 325 tanuló közül 189 (58,3% ‐ tavaly 55,3%) lapunk feladatmegoldója.
A tavalyi versenyen helyezést nyert 34 III. osztályú tanuló közül 29 bekerült a döntőbe (3 nem indult el az idén); a múlt évi Arany Dániel versenyen helyezést elért 24 II. osztályú tanuló közül 19 ez idén is a döntőbe jutott (2 nem indult el ez idén).

 

Kimutatás az 1957. évi Országos Matematikai Tanulmányi Verseny I. fordulójáról
megyék, városok és iskolafajok szerint

Beadott dolgozatokDöntőbe került
gimnáziumip.techn.összesengimnáziumip.techn.összeseniskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanuló   1. Baranya.....342‐‐34211‐‐11I. Pécs város.....37632961051113242. Bács-Kiskun.....54512647510116113. Békés.....111531141216746‐‐464. Borsod.....690‐‐690410‐‐410II. Miskolc város.....45946081192413375. Csongrád.....654‐‐65439‐‐39III. Szeged város.....35833869629123116. Fejér.....45221666817132107. Győr-Sopron.....916244713209625‐‐6258. Hajdú-Bihar.....541‐‐54112‐‐12IV. Debrecen város.....66433599929345139. Heves.....488‐‐48826‐‐2610.Komárom.....86612968391241111. Nógrád.....2211832913‐‐1312. Pest.....210319101124121151313. Somogy.....69718710535‐‐3514. Szabolcs.....1097‐‐109733‐‐3315. Szolnok.....131791914188915‐‐91516. Tolna.....433‐‐43322‐‐2217. Vas.....9110151011545‐‐4518. Veszprém.....915012210172714‐‐71419. Zala.....21812434224‐‐24 Vidék.....141185829328170218672171101982190V. Budapest*4371316205599183412561040135Összesen18425714553322931041062961629122325*A gimnáziumokhoz sorolva 1 katonai középiskola 16 versenyzővel, akik közül 2 bekerült a döntöbe.

Alább közöljük az I. fordulón kitűzött 3 feladatot megoldásokkal és megjegyzésekkel.
 

1. feladat. Bizonyítsuk be, hogy ha a+b pozitív szám, akkor
ab2+ba2≥1a+1b.

I. megoldás: A bizonyítandó állítás írható az
ab2+ba2-1a-1b≥0(1)
alakban.
A baloldalt közös nevezőre hozva, majd a számlálót ismételten tényezőkre bontva nyerjük, hogy
a3+b3-ab2-a2ba2b2=(a+b)(a2-ab+b2)-ab(a+b)a2b2==(a+b)(a2-ab+b2-ab)a2b2,


vagyis egyenlőtlenségünk így is írható
(a+b)(a-b)2a2b2≥0.(2)

Mivel az a=0, b=0 értékek ki vannak zárva (mert különben az adott egyenlőtlenség értelmetlen volna), a2b2 mindig pozitív, (a-b)2 nem lehet negatív, (a+b) pedig a feltétel szerint pozitív, és így az (1)-gyel egyenértékű (2) helyessége nyilvánvaló. Az egyenlőség jele csak akkor érvényes, ha a=b.
 

Megjegyzés. Lényegében ugyanezeken az átalakításokon keresztül jutunk célhoz akkor is, ha bizonyítandó egyenlőtlenséget összevonás után a feltétel szerint pozitív a2b2a+b értékkel szorozzuk, és azután redukáljuk 0-ra, vagy ha a két oldal különbségét úgy képezzük, hogy a két oldal megfelelő tagjainak különbségét képezzük először, amikor is egyszerű módon adódik a tényezőkre bontás. Lényegében ehhez az eljáráshoz csatlakozik a következő megoldás.
 

II. megoldás: Egyenlőtlenségünk
pu+1pv≥u+v
alakban írható, ahol a p=a2b2, u=1a, v=1b. Vizsgáljuk meg, hogy milyen esetekben áll fenn ez az egyenlőtlenség, ha p≥1, és u>0. A két oldal különbsége (mely tehát nem lehet negatív):
pu+1pv-u-v=(p-1)u+(1p-1)v=(p-1)(u-vP).
Ez 0, ha p=1. Ellenkező esetben az első tényező feltétel szerint pozitív, tehát a második sem lehet negatív:
u≥vpazaz, mivelu>0,p>0,p≥vu.
Az egyenlőtlenség tehát helyes, ha p sem 1-nél, sem vu-nál nem kisebb. A versenyfeladat esetében feltehetjük, hogy a≥b, a feladat feltétele szerint pedig a>-b. A kettőből ekkor
a≥|b|,a|b|≥1,a2b2≥1.
Így p=a2b2, u=1a, v=1b választás mellett
p≥1,másrésztp=a2b2=a|b|⋅a|b|≥a|b|≥a|b|≥ab=vu
végül az a|≥|b|≥0 (és nyilván a≠0) folytán u=1a>0. Így alkalmazható eredményünk, és a bizonyítandó egyenlőtlenség, helyességét adja. Ezzel állításunkat egy valamivel általánosabb egyenlőtlenség következményeként kaptuk.
 

Megjegyzés. Számos megoldás nem volt teljes értékű, mert szerzője, szorozva vagy osztva (a+b)-vel, nem hangsúlyozta, hogy a+b>0. Természetesen kimondottan hiba, ha a versenyző kiemelte, hogy a+b≠0., mert ezzel elárulta, hogy nincs tisztában azzal, hogy egyenlőtlenségek szorzásánál (osztásánál) lényeges a szorzó (ill. osztó) előjele.
Sajnos, még gyakoribb volt az a megsemmisítő hiba, hogy versenyző ab-vel mint pozitív számmal szorzott vagy osztott, holott ab előjeléről nem tudunk semmit.
 

2. feladat: Egy téglalap mindegyik oldalára mint alapra rajzoljunk kifelé olyan téglalapot, amelynek magassága az alap n-ed része. Egyenlő kerületű téglalapokból indulva ki megválasztható-e n értéke úgy, hogy az 5 téglalapból álló idom területe mindig ugyanakkora legyen?
 

I. megoldás: Tekintsünk két tetszőleges, egyenlő kerületű téglalapot. Legyenek az oldalak a, b, ill. c, d, ahol a+b=c+d.
A feladat szerint megalkotva mindkettőből az 5 téglalapból álló idomot, ezek területe egyenlő :
ab+2(a⋅an+b⋅bn)=cd+2(c⋅cn+d⋅dn),
vagyis
ab+2a2+2b2n=cd+2c2+2d2n.

Mindkét oldalt n-nel szorozva, és rendezve
n(ab-cd)=2[c2+d2-(a2+b2)]==2[(c+d)2-(a+b)2-2cd+2ab].



Mivel a feltétel szerint c+d=a+b, azért
n(ab-cd)=2(2ab-2cd)=4(ab-cd),
és így feltéve, hogy ab-cd≠0,
n=4.

Ha ab-cd=0, akkor az a+b=c+d=s jelölést használva, b=s-a, d=s-c, és így
a(s-a)-c(s-c)=as-a2-cs+c2=s(a-c)-(a2-c2)==(a-c)(s-a-c)=0,


ahonnan, vagy c=a, vagy c=s-a. Mindkét esetben a két téglalap egybevágó, és n értéke ez esetben tetszőleges.
 

II. megoldás: Legyenek a téglalap oldalai a és b. A feladat szerint képezett 5 téglalapból álló idom területe
T=ab+2a2n+2b2n.

Adjunk a jobboldalhoz 4abn-4abn-et, hogy behozhassuk az állandó a+b kifejezést:
T=ab+2a2n+4abn+2b2n-4abn=2(a2+2ab+b2)n+ab-4abn==2(a+b)2n+ab(1-4n).



Ha feltesszük, hogy a+b állandó, akkor a jobboldal első tagja nem függ a téglalap alakjától, a második tag azonban akkor és csakis akkor nem függ külön-külön az a és b oldaltól (vagyis a téglalap alakjától), ha értéke 0, vagyis (mivel ab≠0)
1-4n=0,
ahonnan
n=4.
Ez esetben T állandó értéke
(a+b)22

 

Megjegyzések: 1. A feladatot megoldó versenyzők legnagyobb része az 1. megoldás szerint dolgozott, de a diszkussziót (ab-cd=0 esetén) már kevés versenyző végezte el. A II. megoldás szerint dolgozók pedig legtöbbnyire csak arra mutattak rá, mindjárt a T=ab+2a2n+2b2n alakban, hogy n=4 esetén T=12(a+b)2 állandó, és egyáltalán nem törődtek azzal, hogy nem lehet-e T más n értékekre is független a téglalap alakjától.
2. Több versenyző rámutatott arra, hogy a feladat minden nehézség nélkül általánosítható a 90∘-os téglalapról α szögű paralelogrammára, oly módon, hogy az oldal n-ed részével toldjuk meg mindkét irányban a szomszédos oldalt. Ez esetben az 5 téglalap mindegyikének területe, és így T is, az n-től független sinα állandóval szorzódik.
 

3. feladat. Adva van egy kör, annak kerületén egy A pont és belsejében egy O pont. Szerkesszük meg a kör kerületén a B és C pontokat úgy, hogy az ABC háromszögbe írt kör középpontja az adott O pont legyen.
 

I. megoldás: Képzeljük a feladatot megoldottnak, a betűzést az 1. ábra mutatja.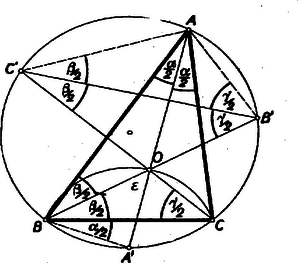
 
 
1. ábra
 

A BO és CO szögfelezők messék a kört másodszor a B', ill. C' pontokban. A kerületi szögek tétele szerint AB'=B'C, és AC'=C'B, és így ugyancsak a kerületi szögek tételének értelmében az OB'AC' négyszögben a B'C' átló felezi a B' és C' csúcspontoknál fekvő szögeket, vagyis a B'C' átló a négyszög szimmetria tengelye. Ebből következik, hogy a négyszög deltoid, és B'C' merőlegesen felezi az AO átlót.
Eszerint az igen egyszerű szerkesztés menete Az AO szakaszt merőlegesen felező egyenes metszi ki a körből a B' és C' pontokat (2. ábra).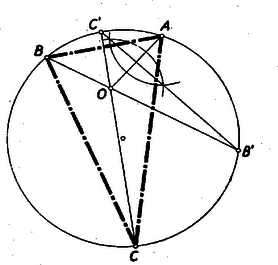
 
 
2. ábra
 

A B'O és C'O egyeneseknek második metszéspontja a körrel szolgáltatja a keresett B, ill. C pontokat.
 

II. megoldás: Még egyszerűbb szerkesztéshez jutunk a következőképpen: Legyen az AO egyenes második metszéspontja a körrel A'. Az A'BO▵-ben a O csúcsnál fekvő ϵ szög az AOB▵ külső szöge (1. ábra). Tehát ϵ=α2+β2. Az A'BC∢ mint kerületi szög α2, és így az A'BO∢=α2+β2=ϵ. Tehát az A'BO▵-ben e két egyenlő szöggel szemben fekvő két oldal is egyenlő, vagyis
A'B=A'O,hasonlóanA'C=A'O.

Eszerint az A' körül A'O sugárral rajzolt kör metszi ki az adott, körből a keresett B és C pontokat (3. ábra).
 
 
3. ábra
 

Megjegyzés: Az itt bizonyított tételt (mely szerint a háromszög köré írt kör két csúcspont közti ívének felezőpontja éppolyan távol van a két csúcsponttól, mint a háromszögbe írt kör középpontjától) lényegében tartalmazta az 1954. évi Arany Dániel versenyen kezdők részére kitűzött 1. feladat (lásd a K. M. L. IX. kötet, 2. sz. 1954. okt., 33. o.), de megtalálható a tétel a Matematikai Versenytételek I. részében is az 1897/2. feladathoz fűzött 2. jegyzetében (42. o.). Néhány versenyző hivatkozott is e forrásokra, de a megoldók zöme bizonyította e tételt.
A bizonyítás tulajdonképpen már az I. megoldásban megtörtént, amikor megmutattuk, hogy az OB'AC' négyszög (1. ábra) deltoid, vagyis B'A=B'O, és C'A=C'O.
 

III. megoldás: Igen szép, szellemes megoldáshoz jutunk (bár nem a legegyszerűbbhöz), ha az előzőknél valamivel többet (Feuerbach-féle kör) használunk fel.
Tekintsük a keresett ABC▵-et valamely A'B'C'▵ talpponti háromszögének, akkor az adott K középpontú és r sugarú k kör az A'B'C'▵ Feuerbach-féle köre (K≡F'). Ismeretes, hogy az A'B'C'▵ magasságvonalai a talpponti háromszög szögfelezői, tehát az adott O pont azonos az A'B'C' háromszög M' magasságpontjával, A pedig az A'-ból kiinduló magasságvonal A'1 talppontja. Ismeretes továbbá, hogy az A'B'C'▵ k' körülírt köre nem egyéb, mint a k Feuerbach-féle körnek 1:2 arányú kivetítése az M'(≡O) centrumból.
Eszerint a szerkesztés menete: Az O(≡M') pont tükörképe a K(≡F') pontra nézve lesz az A'B'C'▵ köré írt k' körnek K' középpontja (4. ábra).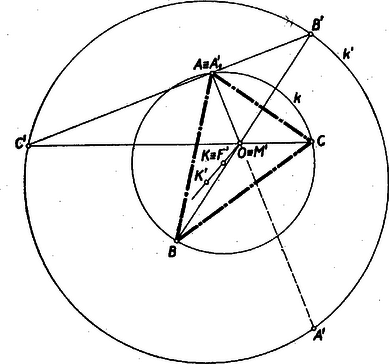
 
 
4. ábra
 

K' körül 2 r sugárral rajzolt kör a k' kör. Az A(≡A'1) pontban OA(≡M'A'1)-ra emelt merőleges egyenes metszi ki a k'-ből a B' és C' pontokat. A B'O(≡B'M') és C'O(≡C'M') egyeneseknek a k körrel való, O(≡M') ponton túl fekvő metszéspontjai a keresett B és C pontok.
 

IV. megoldás: Könnyen nyerhető egy szerkesztés, de távolról sem egyszerű szerkesztés, Euler egy tételén keresztül, melyet a versenyzők nagy része ismert és felhasznált, pl. a következő módon:
Ha az adott kör középpontja K, sugara r, a keresett ABC háromszögbe írt kör sugara ϱ, és OK=d, akkor Euler tétele szerint (lásd pl. Matematikai Versenytételek I. rész, 41. o.)
2rϱ=r2-d2=(r+d)(r-d)
ahonnan
2r:(r+d)=(r-d):ϱ,
és így ϱ az adatokból negyedik arányosként könnyen megszerkeszthető (5. ábra).
 
 
5. ábra
 

Az A pontból az O körül ϱ sugárral rajzolt körhöz szerkesztett érintők metszik ki az adott körből a keresett B és C pontokat (6. ábra).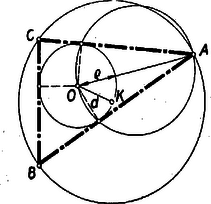
 
 
6. ábra
 

Az idézett helyen megtaláljuk annak bizonyítását is, hogy az Euler-összefüggés teljesülése esetén a kerület bármely A pontjából indulva ki a BC egyenes is érinti az O középpontú ϱ sugarú kört, tehát az ABC háromszög megfelel a feladat feltételeinek.
Mindig van egy és csakis egy megoldás, mert 2r>r+d miatt r-d>ϱ, és így a ϱ sugarú kör mindig az r sugarú kör belsejében van.1
 

Megjegyzés: E tétel különben, mint láthattuk (gyakorlati szempontból tekintve) elég körülményes szerkesztéshez vezet, még akkor is, ha negyedik arányosként szerkesztjük meg közvetlenül a ϱ-t. A megoldók legnagyobb része azonban ügyetlenebbül a d2=r(r-2ϱ) alakból, az adott d és r szakaszokból, a derékszögű háromszöggel kapcsolatos mértani középarányosság felhasználásával szerkesztette meg az r-2ϱ szakaszt, amelyből r-(r-2ϱ)2-ként kapta meg a ϱ-t.
1Szerkesztő megjegyzése: Számos versenyző ‐ főleg lapunk olvasói ‐ használta fel e tételt, amelyre lapunk a közelmúltban kétszer is (XIII. kötet 3. sz. 1956. november, 96. o., és XIII, kötet 5. sz. 1956. december 143. o.) hivatkozott. Kitűnik ebből, hogy a középiskolai matematikai irodalom ismerete kétségkivül előnyt jelent a versenyzőknek, amint erre lapunk állandóan rámutatott.
Jelen esetben azonban sem az Euler-tételre, sem a Feuerbach-féle körre nem volt szükség, hanem az I. gimnáziumban tanult egyszerű szögösszefüggések vezettek el a legegyszerűbb, legelegánsabb szerkesztéshez, amint azt az I. és II. megoldásban láttuk.