Cím: A szögharmadolás kérdéséről.- 1. közlemény
Szerző(k):  Surányi János 
Füzet: 1957/április, 97 - 107. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismerkedés a problémával

 

1. Bizonyára mindenki hallott már arról, hogy a szög harmadolása, vagyis három egyenlő részre osztása vonalzóval és körzővel nem oldható meg. Ez elég meglepő állítás. A hasonló feladat szakaszokra megoldható: egy egyenes szakasznak meg tudjuk szerkeszteni az n-ed részét, akármilyen természetes szám is n. Szögeknél is meg tudjuk szerkeszteni akármilyen szögnek a felét, a harmadrészét megszerkeszteni azonban általában nem sikerül.
Azt mondtuk, hogy ,,általában'', hiszen vannak speciális szögek, amelyeknek harmadrészét meg lehet szerkeszteni. Ilyenek pl.: a 90∘, 45∘, 180∘, mert 30∘-os, 15∘-os, illetőleg 60∘-os szöget tudunk szerkeszteni, de ilyen pl. a 36∘ is, mert kétszerese, a 72∘ éppen 12∘-kal, tehát a 36∘ harmadrészével, nagyobb 60∘-nál: (Maga a 36∘ is megszerkeszthető, pl. mint a szabályos tízszög egy oldalához tartozó középponti szög.)
A szög harmadolásán azonban egy olyan eljárást értenénk, amely alkalmas tetszés szerinti szög harmadrészének megszerkesztésére. Ha van csak egy olyan szög is, amelynek a harmadrésze nem szerkeszthető meg, akkor természetesen általános eljárás sem lehetséges tetszés szerinti szög harmadrészének megszerkesztésére.
Egy Pappustól (alexandriai görög matematikus 300 évvel i. u.) ránkhagyott észrevétel (amely állítólag i. e. V. századból való) úgy látszik, mintha kezünkbe is adná a feladat megoldását. Mérjünk egy szög egyik szárára a csúcstól valamilyen AB=t távolságot (1. ábra), a B végpontból messük el t távolsággal a másik szárat, majd a C metszéspontból ismét t távolsággal az elsőt, legyen az újabb metszéspont D. A háromszögek külső szögére vonatkozó tétel alapján látható, hogy a C pontnál keletkező a szög háromszorosa annak a szögnek, amelyből kiindultunk.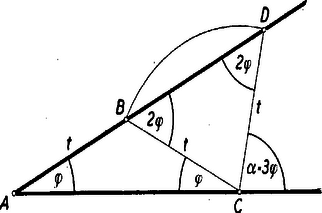
 
 
1. ábra
 

Ha ezt az ábrát sikerül az α szögből kiindulva rekonstruálni, akkor harmadoltuk α-t. Próbáljuk ezt meg. A D pontot tetszés szerint vehetjük fel. B rajta lesz a C körül D-n át húzott körön. Rajzoljuk meg ezt a kört, és hosszabbítsuk meg a szög D-t nem tartalmazó szárát a C csúcson túl (2. ábra).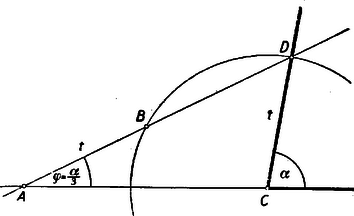
 
 
2. ábra
 

Most már csak úgy kell D-n át egy egyenest húzni, hogy annak a kör és a meghosszabbított szögszár közé eső darabja CD hosszúságú legyen. Ezt azonban egy vonalzó segítségével megtehetjük, ha annak éle mentén előre kijelöljük a CD távolságot. (A vonalzót egy egyenes szélű papírcsík is helyettesítheti.) Ezután egy kis ügyességgel elhelyezhetjük a vonalzót úgy, hogy a két jel a szögszárra, illetőleg a körre essék, az éle pedig átmenjen a D ponton. Ha ez sikerül, akkor meghúzzuk az AD egyenest, és megkaptuk α hamadrészét. Közben csak körzőt és vonalzót használtunk, a vonalzót azonban olyan körmönfont módon, amit nem szoktunk szerkesztésnek elfogadni: kijelöltünk rajta két pontot, és azután úgy igyekeztük elhelyezni, hogy azok megrajzolt vonalakra kerüljenek, éle pedig egy adott ponton menjen át. Egy ilyen műveletet nem tekintünk szerkesztési lépésnek.
2. A probléma egy másik megközelítése volna számításhoz folyamodni. Egy szöget helyettesíthetünk szerkesztés szempontjából a cosinusával. Ha ugyanis egy α szög van adva, akkor egyik szárára rámérve egy tetszés szerinti e távolságot, megszerkeszthetjük ennek p vetületét a másik száron. Ezzel rendelkezésünkre áll az α=cos α=Pe arány (3. ábra).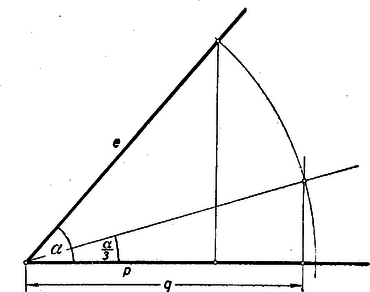
 
 
3. ábra
 

Ha abból meg tudjuk szerkeszteni az x=cosα3 arányt (tehát két ilyen arányban álló távolságot), akkor megszerkeszthetjük azt a q távolságot, amelynek aránya e-hez cosα3, amelyre tehát q=ecosα3 . Ezt rámérve egy e sugarú kör egy sugarára, a végpontjában merőlegest állítunk. Ennek a körrel való metszéspontjához vezető sugár α3 szöget zár be az előbbi sugárral. A cosα3 érték kiszámítására felhasználhatjuk a könnyen igazolható
cos3φ=4cos3φ-3cosφ
összefüggést. Itt φ helyére α3-at írva, és használva a fenti jelöléseket a
4x3-3x-α=0(1)
egyenlethez jutunk. Ez ismét nem vezet el egy szerkesztés megtalálásához. Első és másodfokú egyenlet gyökeit meg tudjuk szerkeszteni, amint ezt a 8. pontban látni fogjuk részletesebben, de harmadfokú egyenletnél nem kínálkozik kézenfekvő áttérés szerkesztésre. Azt fogjuk majd belátni, hogy bizonyos nyilvánvaló esetektől eltekintve ilyen áttérés nem is lehetséges.
Mielőtt azonban továbbmennénk, maradjunk egy pillanatra az (1) egyenletnél. Ennek általában három gyöke lehet1 és mindegyikhez még 2‐2 olyan szög tartozhat, amelyeknek ez a cosinusa. Ez megfelel annak, hogy α is általában két lényegesen különböző szögnek a cosinusa, és az e két szögnél 360∘ és 720∘-kal nagyobb szögek ugyan már nem lényegesen különböző szögek, de harmadrészeik már lényegesen különbözők.
Ha ismerjük az egyenlet összes gyökeit, ezek közül már nem nehéz kiválasztani az adott szög harmadrészét. Mi van azonban, ha az (1) egyenletnek egyik x1 gyökét sikerült megszerkeszteni, de az nem az adott szög harmadának cosinusa? Megszerkeszthető-e ekkor a keresett harmadrész cosinusa is? Mivel x1 gyöke az egyenletnek, azért
4x13-3x1-α=0.
Ezt az (1) egyenletből levonva, α kiesik, és a maradó különbségből x-x1 kiemelhető:
(x-x1)[4(x2+xx1+x12)-3]==(x-x1)[4x2+4xx1+(4x12-3)]=0.(2)

A maradó másodfokú tényező együtthatói x1-ből és a régi együtthatókból összeadás, kivonás, szorzás segítségévél számíthatók ki; ennek a tényezőnek gyökei között szerepel a szerkesztendő szög cosinusa. Másodfokú polinom gyökeit azonban, ha vannak, meg tudjuk szerkeszteni, ha az együtthatói ismertek, azok pedig esetünkben ‐ mint a 8. pontban látni fogjuk ‐ egszerkeszthetők, ha x1 megszerkeszthető.
A most alkalmazott módszerrel belátható, hogy ha egy tetszés szerinti algebrai egyenletnek van egy gyöke, akkor az ahhoz tartozó gyöktényező kiemelhető a 0-ra redukált egyenlet többtagújából. A visszamaradó tényező együtthatói a már megtalált gyökből és a régi együtthatókból összeadás, kivonás, szorzás segítségével számíthatók ki.
Az állítást mi csak harmad- és másodfokú egyenletre fogjuk alkalmazni.
 

Szerkesztés körzővel és vonalzóval

 

3. A fentiekben kiderül, hogy nem elég megmondani, hogy szerkesztési eszközül csak körzőt és vonalzót engedünk meg, meg kell azt is mondanunk, hogy ezekkel milyen lépések végzését engedjük meg. Bár a lehetséges szerkesztések igen változatosak, sokfélék lehetnek, mégis mindössze néhány egyszerű lépésre vezethetők vissza, amelyeket azután többször alkalmazhatunk a legkülönbözőbb sorrendben és helyeken. Összesen öt ilyen elemi lépésre vezethető vissza minden szerkesztés. Vonalzóval
1. két adott ponton át egyenes szerkeszthető, és
2. megszerkeszthető két egyenes metszéspontja.
Körzővel
3. adott pont körül adott sugarú kör szerkeszthető,
4. megszerkeszthető két körnek a két (különböző) metszéspontja, végül körzővel és vonalzóval megszerkeszthető
5. egy egyenes és egy kör két (különböző) metszéspontja.
Természetesen megengedhetnénk más lépésék végzését is vonalzóval és körzővel. Hogy miket engedünk meg, az tisztán megállapodás kérdése. A fönti megállapodások alapján végezhető szerkesztések összessége megegyezik azzal, amit a régi görögök megengedett szerkesztésnek tekintettek, ahogyan az például Euklidesnél megtalálható (bár már korábban is ismeretes volt). Szokás is ezeket euklideszi szerkesztéseknek nevezni. Az, hogy ma is ugyanúgy határoljuk körül a szerkeszthetőség fogalmát, talán nem is annyira a hagyományok tiszteletén múlik, mint azon, hogy ilyen meghatározás mellett, a szerkeszthetőségre igen egyszerű kritérium adódik (amit a 8. pont tételében mondunk ki).
Próbáljunk meg néhány szerkesztést ezen alapszerkesztésekig szétbontani.
Adott egyenesre adott pontjából egy adott távolságot úgy mérhetünk rá, hogy a pont körül az adott szakasszal mint sugárral kört rajzolunk (3. alapszerk.), majd kijelöljük az egyenes és a kör metszéspontjait (5. asz.).
Adott szakasz felező pontjának megszerkesztése így bontható szét: Egy szakaszt a két végpontjával adhatunk meg. A szakasz mindkét végpontja körül a szakasszal mint sugárral kört rajzolunk (kétszer a 3. asz.), megkeressük a két kör metszéspontjait (4. asz.), ezen a két ponton át egyenest rajzolunk, továbbá a szakasz két végpontján is (kétszer az 1. asz.), végül kijelöljük a két egyenes metszéspontját (2. asz.).
Eközben megszerkesztettük a szakasz felező merőlegesét is (a körök metszéspontjait összekötő egyenesben).
Hiába próbálnók azonban a vonalzó két pontjának kijelölését2 vagy az így megjelölt vonalzó részbeli használatát az 5 alapszerkesztésből összetenni. Így a fenti szerkesztés nem körző-vonalzós szerkesztés a most mondott értelemben, nem euklideszi szerkesztés, ahhoz képest a szerkesztés körének egy lényeges bővítését jelenti.
Hangsúlyoztuk az utolsó két alapszerkesztésnél, hogy két különböző metszéspontot tudunk megszerkeszteni. Ha tehát a két kör érinti egymást, illetőleg az egyenes érinti e kört ‐ bár akkor az, érintési pont tekinthető összeeső két metszéspontnak ‐ mégsem tekintjük megszerkesztettnek pusztán azáltal, hogy a két érintkező vonalat megrajzoltuk.
Tudjuk persze, hogy más úton mind a két esetben megszerkeszthető az érintési pont. Az előbbiben a körök középpontját összekötő egyenes metszi ki a körökből, az utóbbiban a kör középpontjából az egyenesre bocsátott merőlegesnek az egyenessel (vagy a körrel) való metszéspontjaként adódik az érintési pont.
Az érintkező körök esetében az 1. és 3. alapszerkesztés közvetlenül elvezet a keresett ponthoz ‐ ha ismeretes a körök középpontja ‐ és a második esetben is elég egyszerű, jól ismert szerkesztés adja a keresett pontot.
A közbevetett ,,ha'' azonban újabb bökkenőt jelent, hiszen egy kör az kör akkor is, ha nincs megjelölve a középpontja. Általában, ha kört említünk, azt adottnak tekintjük a középpontjának kijelölése nélkül is. Ha az is ismeretes, ezt külön adatnak tekintjük, és külön megemlítjük.
4. Abból a szempontból ez a megjegyzés sem nagyon lényeges, hogy ha a kör ismert, megszerkeszthetjük a középpontját is. Két tetszés szerinti nem párhuzamos egyenessel metsszük a kört; az egyenesekből kimetszett húrok felező merőlegeseinek metszéspontja a kör középpontja. A kimetszett húrok kijelölése kétszer az 5. alapszerkesztés alkalmazása, a felező merőleges megszerkesztéséről fentebb már volt szó, végül ezek metszéspontja a 2. alapszerkesztéssel adódik.
Minden rendben lenne tehát, csak éppen az elindulásnál van baj. Itt két tetszés szerint húzott segédegyenesre van szükség, azonban mindegyik alapszerkesztés adott pontokból, adott egyenesekből, adott körökből szerkeszt meg jól meghatározott pontokat, egyeneseket, köröket.
Ha a körön kívül szerepelnek még egyenesek, pontok is, azokból kiindulva általában már el tudunk jutni mindig csak adott vagy korábban már megszerkesztett elemeket használva fel a célnak megfelelő segédelemekhez. Ha azonban a körön kívül semmi nincs adva, akkor ilyen kiutat sem találunk.
Ez komoly hiányosság, mert szerkesztésekben nagyon gyakran elkerülhetetlen segédkörök, segédegyenesek, segédpontok szerepeltetése, amelyeket bizonyos tág korlátok között tetszés szerint veszünk fel.
Ezt a hiányt azzal küszöböljük ki, hogy egy szöget, pl. egy derékszöget, vagyis két egymásra merőleges egyenest, és az egyiken egy, a metszéspontjuktól különböző pontot mindig hozzáveszünk a szerkesztés kiindulására szolgáló adatokhoz. Ezekből már tetszés szerinti sűrűségben tudunk további pontokat és egyeneseket szerkeszteni az egész síkban.
Az egyenesek metszéspontjától az adott pontig terjedő szakaszt az egyik végpontból kiindulva ismételten felmérhetjük akárhányszor az egyenesre, amint azt fentebb részleteztük. Ezután a keletkező szakaszokat felezhetjük, majd az így keletkezőket ismét, és így tetszés szerinti sűrűségben kaphatunk pontokat az egyenesen. A közben segédszerkesztésként kapott szakaszfelező merőlegesek, párhuzamos egyenesek szintén tetszés szerinti sűrűségben.
Az egyik egyenesen adott szakaszt a másikra is rámérhetjük, ott megismételhetjük az elsőn végzett szerkesztéseket. Ekkor már két egymásra merőleges egyenesseregünk van. Ezek segítségével bármilyen igénynek megfelelő sűrűségben tudunk pontokat megszerkeszteni egy síkban (annak abban a részében, amelyben a szerkesztéshez egyáltalán szükség lehet rá), csak kellő sokszor kell a felezéseket megismételni. Ezek felhasználásával már minden igénynek megfelelő segédegyenes és kör előállítható.
Hangsúlyozzuk, hogy nem tekintettük itt a vég nélkül folytatott felezésekkel származó összes egyeneseket és pontokat megszerkesztettnek, hiszen végtelen sok szerkesztési lépés elvégzéséhez végtelen idő kellene, ami nem áll rendelkezésünkre. A szerkesztés kivitelezhetőségéhez tehát mindig szükséges, hogy az véges számú lépésből álljon.
Lássuk még adott pontból adott egyenesre bocsátott merőleges szerkesztését, amelyre fentebb szükség volt. A szokásos eljárás az, hogy az adott pont körül olyan segédkört szerkesztünk, amely metszi az egyenest. Ezután a kimetszett húr felezőmerőlegese megadja a keresett merőlegest, mert átmegy a kör középpontján, vagyis az adott ponton. A segédkör helyett most adott sugárral kell kört rajzolni. Erre használhatjuk a derékszög egyik szárán levő szakaszt. Ha az azzal rajzolt kör nem metszi az egyenest, akkor az adott szakasz többszöröseit szerkesztjük meg, amíg egy akkorához nem jutunk, amelyik már nagyobb, mint az adott pont távolsága az adott egyenestől, és ezt használjuk segédkör sugarául (4. ábra).
 
 
4. ábra
 

Ajánljuk az olvasónak, hogy még néhány egyszerű szerkesztésen (pl. szögmásolás, szögfelezés, adott szakasz mint oldal fölé négyzet szerkesztése, körhöz kívül fekvő pontból érintő szerkesztése stb.) próbálja ki, hogyan lehet azt a most megengedett lépésekből összetenni.
Mindjárt hangsúlyozzuk azt is, hogy mindaz, amit eddig elmondottunk, nem azt jelenti, hogy ezután, ha szerkesztünk, nem szabad találomra alkalmas segédkört, segédegyenest húzni, pontot kijelölni, hanem egy előre megrajzolt derékszögből és szakaszból kiindulva kell mindig a segédelemeket szerkeszteni.
Szerkeszteni természetesen továbbra is ugyanúgy fogunk, mint eddig tettük, a fenti meggondolásoknak az az értelme, hogy ha csak egyszer veszünk segítségül két merőleges egyenest és az egyiken egy pontot, akkor is már megszerkeszthetjük mindazt, amit akárhány tetszés szerint választott segédpont, segédegyenes és segédkör segítségével szerkesztünk. Ennek a tényleges keresztülvitele bonyolítaná a szerkesztést, viszont ha az összes lehetséges szerkesztéseket akarjuk áttekinteni, akkor ez könnyebb, ha csak az említett 3 segédelemet kell számba venni, mintha akármennyi előfordulhat.
Hasonló a helyzet, mint a háromszögvonalzókkal, amelyeket gyakran alkalmazunk párhuzamosok, merőlegesek megrajzolásához, 30∘, 45∘, 60∘-os szögek előállításához. Igaz, hogy a megengedett szerkesztési lépések között ezek egyike sem szerepel, de mindaz, ami háromszögű vonalzóval meghúzható, megszerkeszthető körzővel és vonalzóval is. Így háromszögvonalzó használatával sem szerkeszthető meg más, mint ami euklideszi értelemben megszerkeszthető.
Mindjárt változik a helyzet, ha pl. a körzőt sem igénylő szerkesztéseket vizsgáljuk. Akkor már csak közönséges, ún. egyélű vonalzót használhatunk (amivel tehát mást nem tehetünk, mint egy éle mellett egyenest húzunk), azonban háromszögeket nem, mert az azokkal végzett szerkesztéseket (merőleges, párhuzamos, a fenti nevezetes szögek) háromszög nélkül csak úgy tudjuk elvégezni, hogy körzőt is használunk.
 

Áttérünk számokra

 

5. Geometriai alakzatok szemléletesek, azonban sokkal nehezebb közöttük általános módszereket találni, mint számok között. A geometriai szerkesztések érdekességét például éppen az adja meg, hogy szinte minden feladat új ötleteket kíván, ritkán lehet első látásra tudni, hogy milyen úton lehet egy feladatot megoldani. Ha azonban sehogy sem boldogulunk, akkor a számokhoz fordulunk segítségül, kiszámítunk egy szerkesztendő adatot, és a számítás eredményét szerkesztjük meg úgy, hogy a kiszámítás közben végzendő műveleteket igyekszünk szerkesztéssel követni.
Még inkább kívánatos tehát a számok nyelvére átültetni a kérdést akkor, amikor az összes lehetséges szerkesztések felől igyekszünk tájékozódni. Ehhez a segítségül vett merőleges egyenespárt és az egyiken kijelölt szakaszt3 mindjárt felhasználhatjuk koordináta-tengelyeknek és távolságegységnek. A továbbiakban minden távolság mérőszámát ezzel az egységgel mérve értjük.
Ezután már pontot, egyenest, kört számokkal tudunk helyettesíteni: Egy pontot a két koordinátájával, tehát két szakasz, előjellel ellátott, mérőszámával jellemezhetünk. Egy egyenest az egyenletével jellemzünk a koordináta-geometriában, egy ilyen egyenletet azonban még sokféle alakra lehet hozni, hiszen tetszés szerint végigszorozhatjuk egy számmal. Ha y szerepel az egyenletben, akkor például iránytényezős alakra hozhatjuk az egyenletet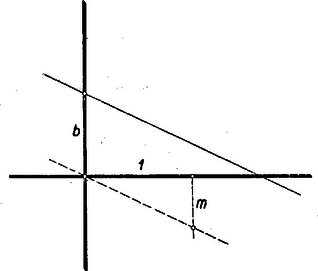
y=mx+b.
Itt b, az y-tengelyből lemetszett rész, közvetlenül leolvasható, m-et pedig úgy kaphatjuk meg, hogy az origón át párhuzamost húzunk az egyenessel, majd az x tengelyen felmért egység végpontjában a tengelyre merőlegest állítunk. Ezen a merőlegesen a párhuzamos egyenesig terjedő szakasz mérőszáma előjellel véve adja az egyenes iránytangensét, m-et (5. ábra.).
 
 
5. ábra
 

Hátra van még az az eset, ha y nem szerepel az egyenes egyenletében. Ekkor az egyenlet
x=a
alakra hozható, az egyenes párhuzamos az y tengellyel, és attól mért (előjeles) távolsága a. Ekkor az egyetlen a számmal jellemezhetjük az egyenest.
6. Végül egy kör egyenlete mindig
x2+y2+hx+ky+1=0(1)
alakra hozható, így a h, k, l számhármassal egyértelműen jellemezhető a kör. Kérdés azonban, ha adva van egy kör, ismertnek tekinthető-e ezzel h, k, l is, vagyis megszerkeszthetők-e a h, k, illetőleg l mérőszámú távolságok, és megfordítva, ezekből a távolságokból a kör előállítható-e a körző és vonalzó megengedett módon való használatával.
A második kérdés az analitikus geometriában is felmerül, és úgy oldjuk meg, hogy az (1) egyenlet átalakításával kiolvashatóvá tesszük a középpont koordinátáit és a kör sugarát:
(x+h2)2+(y+k2)2=(h2)2+(k2)2-l.(2)

A K középpont koordinátái innen -h2 , -k2 és az OK szakasz megadja a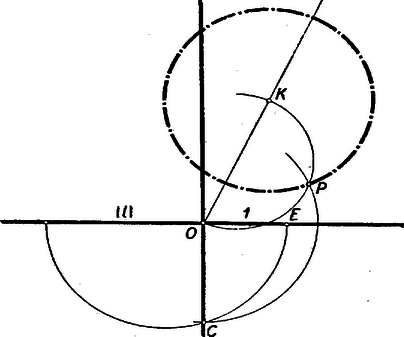
(h2)2+(k2)2távolságot is. Azr=(h2)2+(k2)2-l
megszerkesztéséhez, megszerkesztjük még a |l| értéket. Ezt az 1+|l| átmérőjű félkörben az átmérő egyikvégpontjától 1 távolságban az átmérőre emelt merőlegesnek a körívig terjedő darabja méri (a 6. ábrán OC).
 
 
6. ábra
 

Megszerkesztését megkönnyítettük azáltal, hogy a tengelyeket használtuk merőlegesekül.
Most már aszerint, hogy l pozitív, vagy negatív, a sugarat az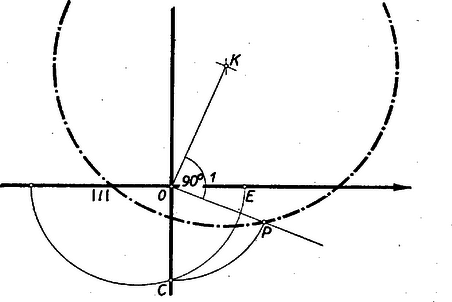
r=OK2-OC2,illetőlegr=OK2+OC2
összefüggésből Pythagoras tétele alapján szerkeszthetjük meg. Az O körül OC sugárral rajzolt kör az első esetben az OK-ra mint átmérőre rajzolt félkörből (6. ábra), a másodikban az OK-ra az O-ban emelt merőlegesből, a keresett kör egy P pontját metszi ki (7. ábra).
 
 
7. ábra
 

Ezután a kör már megszerkeszthető.
Ha l pozitív és OC>OK,(vagyis hal>(h2)2+(k2)2), akkor a szerkesztés nem végezhető el, de (2)-ben is negatív szám áll az egyenlet jobb oldalán, s így nincs is olyan x, y számpár, amelyre az egyenlet teljesül, vagyis az egyenletnek nem felel meg kör.
Fordítva, ha egy kör van adva, akkor először megszerkesztjük középpontját. Ennek kétszeres koordinátái mindjárt megadják h-t és k-t is, |l|-t pedig a 6., illetőleg 7. ábra szerkesztésének ellenkező irányban való követésével kapjuk, aszerint, hogy O a körön kívül vagy belül van. Az előbbi esetben l pozitív, utóbbiban negatív. (Az E-n és C-n átmenő félkör középpontját a CE szakasz felező merőlegese metszi ki az x tengelyből.)
 

A szerkeszthetőség ismérve

 

7. Ezzel eljutottunk ahhoz, hogy a szerkesztés kiindulásához szolgáló adatokat számokkal tudjuk helyettesíteni: minden pontot egy (x;y) számpárral; egy egyenes vagy egy (m;b) számpárral (ha az egyenes metszi az y tengelyt), vagy egy a számmal (ha párhuzamos az egyenes az y tengellyel); végül minden kört egy (h;k;l) számhármassal helyettesíthetünk, ahol4
l<(h2)2+(k2)2,
ha valóban körből indultunk ki.
Szerkesztési lépések alkalmazása újabb pontokhoz, egyenesekhez, körökhöz vezet, vagyis ‐ a számok oldaláról nézve a kérdést ‐ ahhoz, hogy a kiindulási számadatokhoz hozzáveszünk újabbakat, a megszerkesztett elemek jellemzőit. Azt vizsgáljuk meg, hogyan keletkeznek ezek az új számértékek az alapadatokból. Ehhez elég azt megvizsgálnunk, hogy az öt alapszerkesztés milyen újabb számadatokat eredményez, hiszen minden szerkesztés ezek ismételt alkalmazásából tevődik össze.
1. alapszerkesztés az (x1,y1), (x2,y2) pontokon átmenő egyenes egyenlete, az x1≠x2,
y=y2-y1x2-x1(x-x1)
alakban írható, tehát
(y2-y1x2-x1,-x1⋅y2-y1x2-x1)
számpár jellemzi. Ha pedig x1=x2, akkor az összekötő egyenes egyenlete
x=x1,
így az x1 számmal jellemezzük az egyenest. Az új adatok tehát alapműveletek (kivonás, szorzás, osztás) segítségével számíthatók ki a régiekből.
2. alapszerkesztés. A két egyenes egyenlete egy-egy elsőfokú, kétismeretlenű egyenlet. Ezek közös megoldása adja a metszéspont koordinátáit. Elsőfokú egyenlet-rendszer megoldása ismét kiszámítható a négy alapművelet segítségével.
3. alapszerkesztés. Ha a középpont koordinátái (u;v) a sugár r, akkor az (1) alakú egyenlet együtthatói
h=-2u,k=-2v,l=u2+v2-r2,
tehát ismét kiszámíthatók az alapadatokból5 a négy alapművelet segítségével.
Vegyük most előre az 5. alapszerkesztést. Legyen az egyenes és a kör egyenlete
px+qy+r=0,x2+y2+hx+ky+l=0.

Az egyenes egyenletét itt úgy értjük, hogy ha y tényleg szerepel az egyenletben, akkor p, q, r az 1, -m, -b értékeket jelenti, ha nem szerepel, akkor a 0, 1, -a értékeket, ahol m és b, illetőleg a az egyenest jellemző számadatok.
Ha az első egyenletből x-et vagy y-t a másodikba helyettesítjük, a másik ismeretlenre egy másodfokú egyenletet kapunk. Anélkül, hogy a számítást részleteiben elvégeznénk, tudjuk, hogy a megoldások, ha megoldható a másodfokú egyenlet (a valós számok körében), ilyen alakban írhatók:
s±t,
hol s és t az adatokból négy alapművelettel kiszámítható számok. (Az oldó képletben szereplő osztót is már s-be beleolvasztva, illetőleg, a gyökjel alá bevive gondoljuk.) Itt tehát kiléptünk az alapműveletek köréből, amennyiben nyilván azokon kívül négyzetgyökvonásra is szükségünk volt. A másik ismeretlent ezután már az elsőfokú egyenletből számíthatjuk, s így az újra
u+vt(3)
alakban adódik, ahol u és v már ismét az adatokból négy alapművelettel kiszámítható számok, t pedig ugyanaz a mennyiség, amely az első ismeretlen kiszámításában szerepelt.
Végül a 4. alapszerkesztés esetében legyen a két kör egyenlete
x2+y2+h1x+k1y+l1=0,x2+y2+h2x+k2y+l2=0.

A kettő különbsége elsőfokú egyenletet ad:
(h1-h2)x+(k1-k2)y+(l1-l2)=0.
A metszéspontok koordinátáit ezután pl. mint az első és harmadik egyenletből álló rendszer megoldásait kereshetjük, és ezek, mint az előbbi esetben, itt is (3) alakúak lesznek.
8. Azt láttuk tehát, hogy az alapszerkesztések nem vezethetnek el akármilyen adatok megszerkesztéséhez, csak olyanokhoz, amelyek az alapadatokból alapműveletekkel és négyzetgyökvonással számíthatók ki. Mivel összetettebb szerkesztések is az alapszerkesztések ismételt véges számú alkalmazására vezethetők vissza, így azt nyertük, hogy csak olyan adatok szerkeszthetők meg, amelyek az alapadatokból a négy alapművelet és négyzetgyökvonás véges sokszori alkalmazásával kiszámíthatók.
Ezzel máris nyertünk bizonyos áttekintést, a körzővel és vonalzóval végezhető szerkesztéseken, és mindjárt felmerül a kérdés, hogy vajon minden ilyen módon kiszámítható számhoz megszerkeszthető-e egy távolság, amelynek ez a mérőszáma. Erre a kérdésre könnyen adódik az igenlő válasz, és ez tartalmazza a 2. pontban felhasznált állításokat másodfokú egyenlet gyökeinek szerkeszthetőségéről, ha az együtthatók szerkeszthetők, továbbá szerkeszthető adatokból négy alapművelettel összetevődő együttható szerkeszthetőségéről. Bármilyen bonyolultan is tevődik össze ugyanis egy szám a megengedett műveletekből, kiszámításához mégis véges számú lépést és minden egyes lépésben csak az összeadás, kivonás, szorzás, osztás vagy négyzetgyökvonás valamelyikét kell végezni adott, vagy már előzőleg kiszámított mennyiségek között. A kérdés eldöntésére tehát elegendő azt megmutatni, hogy ezeknek a műveleteknek az eredményei megszerkeszthetők.
Két adott távolságból, a-ból és b-ből, összegük és különbségük megszerkesztése nem igényel különösebb magyarázatot.
A szorzatot és a hányadost megszerkeszthetjük az egységnyi távolság felhasználásával pl. a következő módon. Legyen OE az egységnyi szakasz az x tengelyen. Mérjük rá az OA=a távolságot az y tengelyre, az OB=b távolságot az x tengelyre. A keletkező hasonló háromszögekből leolvasható (8. ábra), hogy a B-ből EA-val párhuzamosan húzott egyenes a szorzat végpontját, az E-ből AB-vel párhuzamosan húzott pedig a hányadosét metszi ki az y tengelyből.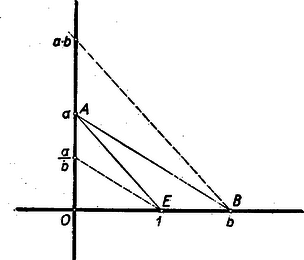
 
 
8. ábra
 

Belátható, hogy a távolságokat előjel figyelembevételével mérve fel a tengelyekre, a műveleti eredmények is helyes előjellel adódnak, de megtehetjük azt is, hogy a szerkesztést a távolságok abszolút értékével végezzük, és külön vesszük figyelembe az előjelet.
Hátra van még egy pozitív távolság négyzetgyökének megszerkesztése, ezt azonban a kör jellemzésével kapcsolatban már el is mondtuk, hogy történhet.
A fentebb nyert feltétel tehát nemcsak szükséges, hanem elégséges is ahhoz, hogy egy számadat szerkeszthető távolság mértékszáma legyen.
TÉTEL: Egy távolság akkor és csak akkor szerkeszthető meg körző és vonalzó segítségével, ha mértékszáma kiszámítható az alapadatokból csupán a négy alapművelet és négyzetgyökvonás véges számú alkalmazásával.
Ezzel meg is találtuk a szerkeszthetőség keresett kritériumát. Cikkünk folytatásában a szögharmadolás kérdésén megmutatjuk, hogyan alkalmazható ez a tétel, ami még jóval több nehézséggel jár, mint első látszatra gondolnánk.
1Csak a valós számok ismeretét tételezzük fel, így kijelentéseink mindig azok körében értendők.

2Szerkesztést mindig egy síkban (általában a rajztáblára feszített rajzlapon) gondoljuk végezni, semmi esetre sem a rajzeszközön.

3Ha az adatok között szerepel legalább. két pont, akkor persze célszerű két adott ponton átmenő egyenest és az egyik pontban erre emelt merőlegest választani ki.

4A fentiekben csak az l>(h2)2+(k2)2 esetet zártuk ki, azonban az l=(h2)2+(k2)2 annak felel meg, hogy a sugár hossza 0, vagyis a kör a középpontjára zsugorodik össze. Ha tehát tényleges körből indultunk ki, akkor ez sem fordulhat elő.

5A ,,2'' szorzó itt nem mint ismert adat lépett fel, viszont tekinthetjük 2u-t és 2v-t is az u+u, ill v+v összegnek. Hasonlóan u2, v2, r2 írható u⋅u, v⋅v, r⋅r alakban, tehát szintén alapművelettel számítható ki. (Egyébként a ,,2''-t mint az egységszakasz kétszeresét alapadatnak is tekinthetnők.)