Kezdőlap


Cím:	Néhány elemi úton megoldható szélsőértékfeladat
Szerző(k):	Berkes Jenő
Füzet:	1957/március, 70 - 74. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szélsőértékfeladatok általában a differenciálszámítás segítségével oldhatók meg. Ez azonban jelenleg nem anyaga a középiskolának. Néhány példát szeretnénk mutatni arra, hogy sokszor reménytelennek látszó szélsőértékfeladatok mégis megoldhatók a differenciálszámítás nélkül is, tehát elemi úton.

1. Adva van egy

a

b

féltengelyű ellipszis. Írjunk bele olyan háromszögeket, melyeknek egyik csúcsa a kistengely végpontja, a szembenfekvő oldal pedig a nagytengellyel párhuzamos. Melyik közülük a legnagyobb területű? (1. ábra)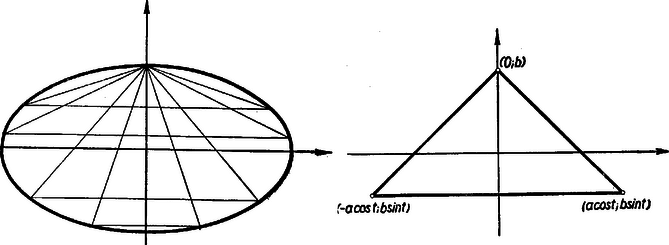

1. ábra 2. ábra

Tudjuk (lásd a III. gimn. tankönyv 1953. 247. old.), hogy az ellipszis megadható a következő paraméteres egyenletrendszerrel:

\begin{matrix} x = a cos t, y = b sin t (- π \leq t < π) . \end{matrix}

Így a 2. ábra szerint a fölrajzolt háromszög kerülete:

\begin{matrix} T = a cos t (b - b sin t) = a b cos t (1 - sin t) . \end{matrix}

(1)

T

függvénye

t

-nek. Az értelmezési tartomány

\begin{matrix} - \frac{π}{2} \leq t \leq \frac{π}{2} . \end{matrix}

Nyilvánvalóan tekinthetjük a

{(\frac{T}{a b})}^{2}

függvényt, ennek ugyanazon a helyen van szélsőértéke mint

T

-nek, hiszen

T

a jelzett intervallumban nem negatív, tehát:

\begin{matrix} y = {(\frac{T}{a b})}^{2} = cos^{2} t {(1 - sin t)}^{2} = (1 - sin^{2} t) {(1 - sin t)}^{2} \end{matrix}

(2)

Ennek a komplikált trigonometriai függvénynek kell már most a szélsőértékét (jelen esetben a maximumát) meghatározni. Bontsuk fel tényezőkre:

\begin{matrix} y = (1 - sin t) (1 + sin t) (1 - sin t) (1 - sin t), \end{matrix}

(3)

szorozzuk meg a függvényt egyelőre határozatlan

m

és

n

pozitív konstansokkal, ekkor nyerjük a

\begin{matrix} z = m n y = m (1 - sin t) n (1 + sin t) (1 - sin t) (1 - sin t) . \end{matrix}

(4)

z

függvény maximumának meghatározása már sikerülni fog. (Nyilván az

y

maximuma ugyanott van.) A négy tényező összege ugyanis

\begin{matrix} (n - m - 2) sin t + m + n + 2. \end{matrix}

(5)

Ez az összeg

t

-től független, ha

\begin{matrix} n = m + 2. \end{matrix}

(6)

Viszont a számtani és a mértani közép relációjából tudjuk, hogy amennyiben egy összeg, mely pozitív mennyiségekből áll, állandó, a tagok szorzata akkor a legnagyobb, ha mind egyenlők, tehát jelenleg, ha

\begin{matrix} m (1 - sin t) = 1 - sin t, n (1 + sin t) = 1 - sin t . \end{matrix}

(7)

(7)-ből és (6)-ból

\begin{matrix} m = 1, n = \frac{1 - sin t}{1 + sin t} = 3 \end{matrix}

következik. Ez utóbbiból

\begin{matrix} 4 sin t = - 2, sin t = - \frac{1}{2}, és így t = - 30^{\circ} . \end{matrix}

A keresett maximális területű háromszög csúcspontjai tehát

\begin{matrix} (0; b), (- \frac{a \sqrt[]{3}}{2}, - \frac{b}{2}) és (\frac{a \sqrt[]{3}}{2}, - \frac{b}{2}) . \end{matrix}

Számítsuk ki a maximum nagyságát is:

\begin{matrix} T_{m a x} = \frac{a \sqrt[]{3}}{2} \cdot \frac{3 b}{2} = a b \frac{3 \sqrt[]{3}}{4} . \end{matrix}

Az ellipszis területe

a b π

lévén, a két terület aránya

\begin{matrix} \frac{3 \sqrt[]{3}}{4 π} \sim 0, 413. \end{matrix}

Megjegyezzük, hogy ebben a feladatban egyszerűbben is célhoz juthatunk a kör és ellipszis közötti affinitás felhasználásával.
Először is könnyű belátni, hogy egy adott körbe írt háromszögek közül a szabályos háromszög a legnagyobb területű. Tekintsünk ugyanis egy körbe írt

A B C

háromszöget, amelynek nincs

60^{\circ}

-os szöge (3. ábra).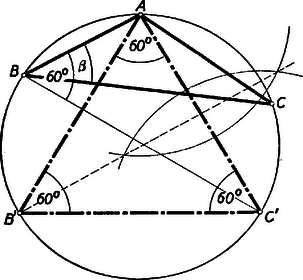

3. ábra

Ennek legalább egyik szöge pl. a

β

szöge kisebb

60^{\circ}

-nál. Ha a

β

szöget alkotó kisebb oldalt (ábránkban az

A B

-t) rögzítjük, és a

C

csúcspontot a körön eltoljuk, amíg

B C'

A B

oldallal

60^{\circ}

-os szöget zár be, akkor az így nyert

A B C'_{▵}

területe nagyobb, mint az

A B C_{▵}

területe, mert a közös

A B

oldalhoz tartozó magasság az előbbiben nagyobb mint az utóbbiban, lévén

B A < B C

, és az

{A C}_{}^{⌢} < {A C'}_{}^{⌢} = 120^{\circ}

. Ha az

A B C'_{▵}

-ben az

A C'

oldalt rögzítjük, és a

B

pontot a körön eltoljuk

B'

-be úgy, hogy

B'

A C'

oldalt merőlegesen felező egyenesbe essék, akkor a

B' A = B' C'

, és így az

A C' B

egyenlőszárú háromszögben az

A C'

alapnál felvett szögek egyenlők, és mivel a

B'

-nél fekvő szög, mint kerületi szög,

60^{\circ}

-os, azért az

A

és

C'

csúcsokban fekvő szögek is

60^{\circ}

-osak, vagyis az

A B' C'_{▵}

szabályos, és azonfelül az

A B' C'_{▵}

területe nagyobb mint az

A B C'_{▵}

területe, mert a közös

A C'

oldalhoz tartozó magasság nagyobb az előbbiben mint az utóbbiban.
Tehát bármelyik, körbe írt, háromszögről, amelynek nem minden szöge

60^{\circ}

-os, legfeljebb két lépésben kimutatható, hogy területe kisebb a körbe írt szabályos háromszög területénél.
Ismeretes, hogy valamely síkidom területe és az affin idom területének aránya állandó (jelen esetben ez közvetlenül leolvasható). Tehát, ha valamelyik síkidom területe a körrendszerben maximális, akkor a megfelelő idom területe az ellipszis rendszerben is maximális. Ha az ellipszis főkörébe írunk szabályos háromszöget, melynek egyik csúcsa a

(0; a)

pont, akkor a szembenfekvő oldal felezi a

(0; 0)

(0; - a)

végpontú főkörsugárt, és így az affinháromszög egyik csúcspontja a

(0; b)

, és e ponttal szemközti oldal felezi a

(0; 0)

(0; - b)

végpontú ellipszis féltengelyt. Tehát a maximális területű háromszög másik két csúcspontja:

\begin{matrix} (- \frac{a \sqrt[]{3}}{2}, - \frac{b}{2}), (\frac{a \sqrt[]{3}}{2}, - \frac{b}{2}) . \end{matrix}

2. Tekintsük az

x^{2} - y^{2} = 1

egyenlő oldalú hiperbola

x > 0

ágát, melynek az

x = a > 1

egyenessel levágott szegmentumába téglalapokat írunk, melynek középvonala az

x

tengelyre esik (4. ábra).

4. ábra

E téglalapok közül melyiknek a területe a legnagyobb?
Nyilván

\begin{matrix} T = 2 y (a - x) = 2 \sqrt[]{x^{2} - 1} (a - x) . \end{matrix}

(8)

Tekintve az

y = {(\frac{T}{2})}^{2}

függvényt

\begin{matrix} y = (x - 1) (x + 1) (a - x) (a - x) . \end{matrix}

A négy tényezős szorzat maximumának kiszámítását kíséreljük meg az előbbi módszerrel. Az első tényezőt

m

-mel, a másodikat

n

-nel szorozva, a tényezők összegéből akkor esik ki

x

, ha

\begin{matrix} m + n - 2 = 0, \end{matrix}

(9)

és akkor lesz még egyenlő is a négy tényező, ha

\begin{matrix} m \cdot (x - 1) = a - x, n \cdot (x + 1) = a - x . \end{matrix}

(10)

(10)-ből

m

-et és

n

-et (9)-be helyettesítve

\begin{matrix} \frac{a - x}{x + 1} + \frac{a - x}{x - 1} - 2 = 0, \end{matrix}

azaz

\begin{matrix} 2 x^{2} - a x - 1 = 0, \end{matrix}

ahonnan

\begin{matrix} x = \frac{a + \sqrt[]{a^{2} + 8}}{4} . \end{matrix}

Ezen a helyen van maximum. Ezen értéket (8)-ba helyettesítve, megkapjuk

T

maximális értékét.
3. Igen érdekes feladat a következő. Az ellipszis mely pontja van a kis tengely végpontjától a legnagyobb távolságra? (5. ábra)

5. ábra

Ismét az első feladatbeli paraméteres egyenletrendszert használva, és mindjárt a

d

távolság négyzetet tekintve

\begin{matrix} f (t) = d^{2} = a^{2} cos^{2} t + {(b sin t - b)}^{2} = a^{2} (1 - sin^{2} t) + b^{2} {(sin t - 1)}^{2} = \\ = (b^{2} - a^{2}) sin^{2} t - 2 b^{2} sin t + a^{2} + b^{2} . \end{matrix}

Mint ismeretes

a^{2} - b^{2} = c^{2}

, ahol

c

a lineáris excentricitás.
Tehát

\begin{matrix} f (t) = - c^{2} sin^{2} t - 2 b^{2} sin t + a^{2} + b^{2} = 0. \end{matrix}

sin t

-ben másodfokú függvény, amelynek az ismeretes képlet szerint

\begin{matrix} sin t = - \frac{b^{2}}{c^{2}} \end{matrix}

helyen van maximuma.

Itt 3 esetet kell megkülönböztetni.
1. eset:

b > c

, akkor

\begin{matrix} sin t = - \frac{b^{2}}{c^{2}} < - 1, \end{matrix}

és így ilyen

t

érték nincs. Maga a függvény az értelmezési tartományban folyton csökken, s így legnagyobb az értéke az intervallum elején

- \frac{π}{2}

-nél, ahol

\begin{matrix} f (- \frac{π}{2}) = d^{2} = - c^{2} + 2 b^{2} + a^{2} + b^{2} = 4 b^{2}, \end{matrix}

tehát

\begin{matrix} d_{m a x} = 2 b, \end{matrix}

azaz a kistengely másik végpontja van a legtávolabb.
2. eset:

b = c

, ekkor

\begin{matrix} sin t = - 1 vagyis t = - \frac{π}{2} . \end{matrix}

Ez tehát ugyanarra az eredményre vezet, mint az 1. eset.
3. eset:

b < c

. Most létezik olyan

t

, melyre

\begin{matrix} sin t = - \frac{b^{2}}{c^{2}}, \end{matrix}

és erre lesz függvényünknek maximuma. Számítsuk ki mekkora ez:

\begin{matrix} f_{m a x} = d_{m a x}^{2} = - c^{2} \frac{b^{4}}{c^{4}} + \frac{2 b^{4}}{c^{2}} + a^{2} + b^{2} = a^{2} + b^{2} + \frac{b^{4}}{c^{2}} = \\ = \frac{a^{2} c^{2} + b^{2} (c^{2} + b^{2})}{c^{2}} = \frac{a^{2} c^{2} + a^{2} b^{2}}{c^{2}} = \frac{a^{4}}{c^{2}}, \end{matrix}

ahonnan

\begin{matrix} d_{m a x} = \frac{a^{2}}{c} . \end{matrix}

Tehát

a

mértani középarányos

c

és

d_{m a x}

között.
Ugyanez a feladat érdekes módon megoldható egészen más gondolatmenettel is. (Lásd a jelen számban kitűzött 820. feladatot.)