Kezdőlap


Cím:	Képek a magyar matematika múltjából, 8.- Rados Gusztáv (1862. febr. 22-1942. nov. 1.) 2., befejező közlemény
Szerző(k):	Obláth Richárd
Füzet:	1957/március, 65 - 70. oldal	PDF \| MathML
Témakör(ök):	Egyéb írások

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(2. befejező közlemény)

Most rátérek Rados elemi geometriai dolgozatainak ismertetésére.
Ha adva van

n

pont a síkban, kössük őket minden lehetséges módon össze, amint az (

n = 7

esetére) az 1. ábrán látható, akkor az ismert ‐ legkülső ‐sokszögön kívül az átlók is meghatároznak egy vagy több

n

-szöget. Ezeket alakjuk miatt csillagsokszögeknek nevezzük.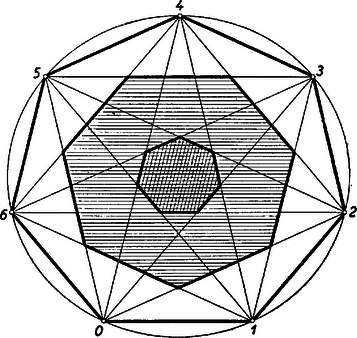

1. ábra

A csillagsokszög, amint neve is mutatja, geometriai fogalom, de pontosan definiálni csak egy fontos számelméleti fogalom segítségével lehet. Nevezzük az

n

pozitív egész számnál kisebb, és hozzá relatív prím pozitív egész számok számát

φ (n)

-nek. Ha tehát pl.

n = 10

, akkor a nála kisebb és hozzá relatív prím pozitív egész számok

1

3

7

9

. Összesen

4

ilyen van, tehát

φ (10) = 4

. Azonnal belátható, hogy ha

n

valamely

p

törzsszámmal egyenlő, akkor

\begin{matrix} φ (p) = p - 1, \end{matrix}

hiszen a törzsszám minden, nála kisebb egész számhoz relatív prím. Hátha valamely

p

törzsszám hatványa? Nyomban látható, hogy

p^{k}

-val közös osztója csak a

p

-vel osztható számoknak van, ezek

\begin{matrix} p,2 p,3 p, ..., p^{k - 1} p, \end{matrix}

ennélfogva

\begin{matrix} φ (p^{k}) = p^{k} - p^{k - 1} = p^{k} (1 - \frac{1}{p}) \end{matrix}

φ (n)

függvény csak pozitív egész számokra van értelmezve; az ilyen függvényeket számelméleti függvényeknek nevezzük. A

φ (n)

számelméleti függvény nevezetes sajátsága, amit itt csak bizonyítás nélkül közlünk, ha

m

és

n

relatív prím számok, akkor

\begin{matrix} φ (m n) = φ (m) φ (n) . \end{matrix}

Ennek alapján könnyű bármely

n

számra

φ (n)

meghatározása, ha

n

törzstényezőre való felbontását ismerjük. Ha

\begin{matrix} n = p_{1}^{k 1} p_{2}^{k 2} \dots p_{r}^{k r}, \end{matrix}

ahol

p_{1}

p_{2}

...

p_{r}

különböző prímszámok, akkor

\begin{matrix} φ (n) & = φ (p_{1}^{k 1}) φ (p_{2}^{k 2}) ... φ (p_{r}^{k r}) = \\ = p_{1}^{k_{1}} (1 - \frac{1}{p_{1}}) p_{2}^{k_{2}} (1 - \frac{1}{p_{2}}) ... p_{r}^{k_{r}} (1 - \frac{1}{p_{r}}) = \\ = n (1 - \frac{1}{p_{1}}) (1 - \frac{1}{p_{2}}) ... (1 - \frac{1}{p_{r}}), \end{matrix}

hiszen két különböző prím szám mindig relatív prím.
E kis számelméleti kitérés után visszatérünk a geometriai feladatra.
Ha a kör kerületét a

\begin{matrix} 0,1,2, ..., n - 1 \end{matrix}

számokkal jelzett

n

egyenlő részre osztják, szabályos

n

-szöget határoznak meg, ha azonban ezeket a pontokat minden lehetségés módon összekötjük, nemcsak egy, hanem

\frac{φ (n)}{2}

számú szabályos sokszöget kapunk, amint ezt

n = 7

esetében az 1. ábra mutatja. Az ,,átlók''-kal meghatározott, az ábrán kisraffozott sokszögeket hívjuk csillagsokszögeknek, ábránkon a három szabályos hétszög

\begin{matrix} 0 1 2 3 4 5 6; 0 2 4 6 1 3 5; 0 3 6 2 5 1 4. \end{matrix}

(5)

0 k

húr ugyanis egy szabályos

n

-szög oldala, ha

(k, n) = 1

, de mivel a

0 k

és

0 \bar{n - k}

húrok ugyanazt a sokszöget határozzák meg, azért számuk, amint már említettük,

\frac{φ (n)}{2}

. Az (5) sorozatban tehát az első az ismert közönséges, szabályos sokszög, a másik kettő pedig a csillagsokszög. Maga a csillagsokszög egy, az adottal koncentrikus kör körül írt érintősokszög, mert a

0 k

húrok egy-egy kör érintői. Radoss¹ a következő kérdésből indul ki: Osszuk fel a kör kerületét

3

egyenlő részre, akkor, amint az a 2. ábráról közvetlenül leolvasható, a beírt és a körülírt háromszög területeinek aránya

\begin{matrix} \frac{1}{4} . \end{matrix}

2. ábra

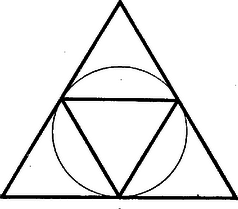Ez racionális szám. Ha

I_{3}

jelenti a beírt,

C_{3}

a körülírt szabályos háromszög területét ‐ és általában

I_{n}

a beírt és

C_{n}

a körülírt szabályos

n

-szög területét ‐ akkor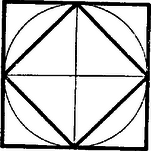

\begin{matrix} \frac{I_{3}}{C_{3}} = \frac{1}{4} . \end{matrix}

A beírt és körülírt négyzetek területeinek arányára is hasonló tétel érvényes, mert, amint ez a 3. ábrából közvetlenül világos

\begin{matrix} \frac{I_{4}}{C_{4}} = \frac{1}{2}, \end{matrix}

tehát szintén racionális.

3. ábra

A szabályos hatszögre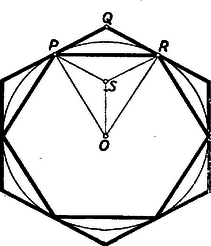

\begin{matrix} \frac{I_{6}}{C_{6}} = \frac{3}{4} \end{matrix}

szintén racionális, de ennek bizonyítása valamivel bonyolultabb (4. ábra).

4. ábra

Legyen

O

a kör középpontja,

P R

a beírt hatszög valamely oldala és

Q

a körülírt hatszögnek

P

és

R

közé eső csúcsa, az

O P R

egyenlőoldalú háromszög középpontja

S

. Minthogy az

O S

P S

R S

egyenesek egyszersmind szögfelezők, azért az

O P Q R

négyszög a négy egybevágó

P Q R

P S O

R S O

P R S

háromszögekre bomlik szét. Ennélfogva

\begin{matrix} \frac{1}{6} I_{6} = 3 P R S és \frac{1}{6} C_{6} = 4 P R S, \end{matrix}

és ebből következik a fenti egyenlőség.
Ha azonban a kör kerületét

5

7

8

9

10

...

egyenlő részre osztjuk, ez az arány sohasem racionális. Radosnak mégis sikerült általánosítani a

3

4

, és

6

-szög esetében fennálló tételt a következő módon:
Ha a körbe írt

\frac{φ (n)}{2}

számú szabályos sokszög területeinek összege

I_{n}

, és a kör körül írt szabályos

n

oldalú sokszög területe

C_{n}

, akkor az

\frac{I_{c}}{C_{n}}

hányados mindig racionális és értéke

\begin{matrix} \frac{I_{n}}{C_{n}} = \frac{φ (n) + ε_{n}}{4} \end{matrix}

ahol

ε_{n}

egyenlő

0

-val, ha

n

-nek van az

1

-től különböző teljes négyzet osztója; ha nincs, akkor

ε_{n}

egyenlő

+ 1

vagy

- 1

, aszerint, amint

n

különböző prím számtényezőinek száma páros vagy páratlan.
Az eddigi

3

4

6

-ra bizonyított tételek csakugyan ennek a tételnek speciális esetei, mert

φ (n)

mindhárom esetben

2

, így csak egy-egy szabályos sokszög van, továbbá

ε_{3} = - 1

ε_{4} = 0

ε_{6} = + 1

, és így

\frac{φ (n) + ε_{n}}{4}

, a kívánt

\frac{1}{4}

\frac{1}{2}

\frac{3}{4}

értékeket adja.
Rados tételének bizonyítása aránylag elemi, és főleg a figyelembe veendő területek meghatározásából áll, ami elemi trigonometriai úton lehetséges, de egy lényeges helyen igénybe vett felsőbb segédeszközöket, úgy, hogy ismertetésétől el kell tekintenem.
Rados még egy további dolgozatában² foglalkozik a szabályos sokszögekkel. Itt is a

3

4

, és

6

oldalú sokszögön tapasztalt törvényszerűséget, terjeszti ki szellemesen, a csillagsokszögek segítségével tetszőleges oldalú szabályos sokszögre.
Az egységsugarú, körbeírt szabályos

n

-szög oldalát

a_{n}

-nel jelölve, amint azt jót tudjuk,

\begin{matrix} a_{3} = 2 sin \frac{π}{3} = 2 \cdot \frac{3^{\frac{1}{2}}}{2} = 3^{\frac{1}{2}}, a_{4} = 2 sin \frac{π}{4} = 2 \cdot \frac{2^{\frac{1}{2}}}{2} = 2^{\frac{1}{2}}, \\ a_{6} = 2 sin \frac{π}{6} = 2 \cdot \frac{1}{2} = 1. \end{matrix}

Eszerint

\begin{matrix} a_{3}^{2} = 3, a_{4}^{2} = 2, míg a_{6}^{2} = 1. \end{matrix}

Szabályos 5-, 8- és 12-szögre már nem adódik ilyen egyszerű eredmény:

\begin{matrix} a_{5}^{2} = \frac{5^{\frac{1}{2}} (5^{\frac{1}{2}} - 1)}{2}, a_{8}^{2} = 2 - 2^{\frac{1}{2}}, a_{12}^{2} = 2 - 3^{\frac{1}{2}}, \end{matrix}

Rados azonban ügyes fordulattal számbaveszi a csillagsokszögeket is. Ezekből

5

8

és

12

oldalú csak egy-egy van. Ezek

a'_{5}

a'_{8}

, ill.

a'_{12}

oldalaira

\begin{matrix} {a'_{5}}^{2} = \frac{5^{\frac{1}{2}} (5^{\frac{1}{2}} + 1)}{2}, {a'_{8}}^{2} = 2 + 2^{\frac{1}{2}}, {a'_{12}}^{2} = 2 + 3^{\frac{1}{2}}, \end{matrix}

és így

\begin{matrix} {(a_{5} a'_{5})}^{2} = 5, {(a_{8} a'_{8})}^{2} = 2, {(a_{12} a'_{12})}^{2} = 1. \end{matrix}

Ebből Rados a következő általános tételt olvassa le, és be is bizonyítja:
Az egységkörbe írható különböző szabályos

n

-szögek (betudva a csillagsokszögeket is) oldalai mérőszámainak négyzetével alkotott szorzat

p

-vel egyenlő, ha

p

az egyetlen prímszám, amellyel

n

osztható és

1

-gyel egyenlő, ha

n

egynél több prímszámmal osztható.
A bizonyítás ismertetésére itt szintén nem térek ki.
Rados egész elemi geometriai problémákkal is foglalkozott. Ő is adott például egy bizonyítást³ arra az ismert tételre, hogy a hegyesszögű háromszögbe beírt háromszögek közül (amelyeknek egy-egy csúcsa az adott háromszög egy-egy oldalán van) a magassági talppontok háromszögének van a legkisebb kerülete.
Teljesen az elemi analitikus geometriához tartozik Radosnak a következő öregkori vizsgálata a kör egyenletéről.⁴ Ha

3

pont

p_{i} (i = 1,2,3)

koordinátái

x_{i}

y_{i}

, akkor könnyen látható, (a bizonyítást az olvasóra bízom), a

3

ponton átmenő kör egyenlete a következő alakban írható:

\begin{matrix} k (x, y) = | \begin{matrix} x^{2} + y^{2}, & x, & y, & 1 \\ x_{1}^{2} + y_{1}^{2}, & x_{1}, & y_{1}, & 1 \\ x_{2}^{2} + y_{2}^{2}, & x_{2}, & y_{2}, & 1 & (6) \\ x_{3}^{2} + y_{3}^{2}, & x_{3}, & y_{3}, & 1 \end{matrix} | = 0, \end{matrix}

hacsak a

k (x, y)

determináns első sorának elemeihez tartozó aldeterminánsak nem mindannyian a

0

-sal egyenlők, amikor az egyenlet a semmitmondó

\begin{matrix} 0 = 0 \end{matrix}

azonosságba megy át. Rados kimutatja, hogy ez az eset akkor és csak akkor következik be, amikor a kör meghatározására megadott 3 pont közül legalább kettő összeesik, minden egyéb esetben (6) valóságos egyenlet.
A bizonyítást bemutatom, hasznos gyakorlat lesz a determinánsokkal való számolásban.
Ha a

k (x, y)

determináns első sorához tartozó aldeterminánsok mindannyian

0

-sal egyenlők, akkor persze az első sor első eleméhez tartozó aldetermináns is

0

, tehát

\begin{matrix} | \begin{matrix} x_{1}, & y_{1}, & 1 \\ x_{2}, & y_{2}, & 1 \\ x_{3}, & y_{3}, & 1 \end{matrix} | = 0. \end{matrix}

Ez geometriailag azt jelenti, hogy a három

P_{i}

pont ugyanazon az egyenesen fekszik.
Ha a három pont egybeesik, nincs mit bizonyítanunk, ha van köztük két különböző, akkor a kérdéses egyenesnek egyenlete

a x + b y + c = 0

alakú, ahol

a

és

b

közül legalább az egyik nem

0

. Ha pl.

b \neq 0

, akkor az egyenlet a

\begin{matrix} y = m x + b \end{matrix}

(7)

alakban is írható. (Ha

b = 0

, akkor csak

x

és

y

szerepét kell megcserélni.)
Mivel (6)-ban az első sor minden eleméhez tartozó aldetermináns, így a harmadik elemhez tartozó is, vagyis ‐ tekintetbe véve, hogy a

P_{i}

pontok koordinátái kielégítik a (7) egyenletet ‐ azt kapjuk, hogy

\begin{matrix} | \begin{matrix} x_{1}^{2} + y_{1}^{2}, & x_{1}, & 1 \\ x_{2}^{2} + y_{2}^{2}, & x_{2}, & 1 \\ x_{3}^{2} + y_{3}^{2}, & x_{3}, & 1 \end{matrix} | = | \begin{matrix} x_{1}^{2} + m^{2} x_{1}^{2} + & 2 & m b & x_{1} + b^{2}, & x_{1}, & 1 \\ x_{2}^{2} + m^{2} x_{2}^{2} + & 2 & m b & x_{2} + b^{2}, & x_{2}, & 1 \\ x_{3}^{2} + m^{2} x_{3}^{2} + & 2 & m b & x_{3} + b^{2}, & x_{3}, & 1 \end{matrix} | = 0. \end{matrix}

vonjuk le a második oszlop.

2 m b

-szeresét és a harmadik

b^{2}

-szeresét az elsőből. Tudjuk, hogy ezáltal a determináns értéke nem változik. Ekkor az első oszlop minden elemében szereplő

m^{2} + 1

tényező a determináns elé kiemelhetjük, és azt kapjuk, hogy

\begin{matrix} (m^{2} + 1) | \begin{matrix} x_{1}^{2}, & x_{1}, & 1 \\ x_{2}^{2}, & x_{2}, & 1 \\ x_{3}^{2}, & x_{3}, & 1 \end{matrix} | = 0, \end{matrix}

ami csak úgy lehet, ha a determináns értéke

0

. A determináns azonban

(x_{1} - x_{2}) (x_{1} - x_{3}) (x_{2} - x_{3})

alakban is írható. (A bizonyítást az olvasóra bízom.) Így a fenti összefüggés azt jelenti, hogy van a pontok között kettő, amelynek az abszcisszája egyenlő. Mivel pedig mindkettő koordinátási kielégítik a (7) egyenletet, ezért ordinátáik is megegyeznek, s így a két pont egybeesik. Ezt kellett bizonyítanunk.
Rados hasonló tételt mond ki és bizonyít be a gömbre is. További eredményei közül még csak egyet említek⁵. A

\begin{matrix} T_{n} (x) = a_{0} + (a_{1} cos x + b_{1} sin x) + (a_{2} cos 2 x + b_{2} sin 2 x) + ... \\ ... + a_{n} cos n x + b_{n} sin n x \end{matrix}

alakú kifejezéseket trigonometrikus polinomoknak nevezzük. Rados róluk a következő tételt bizonyította be.
Ha az

\begin{matrix} a_{0},a_{1},a_{2},...,a_{n}, \\ b_{1},b_{2},...,b_{n} \end{matrix}

együtthatók mindannyian egész számok, ha továbbá a

\begin{matrix} T_{n} (x) = 0 \end{matrix}

trigonometrikus egyenlet összes gyökei valós számok, akkor ezek mindannyian a

π

-nek (Ludolf-féle szám) racionális többszörösei (a szöget ívmértékben mérve).
Radosnak a felemlítetteken kívül is számos dolgozata van, de tárgyuk kívül esik ifjú olvasóink érdeklődési körén.

\begin{matrix} * \end{matrix}

Az eddigiekben mindig csak a matematikusról volt szó, aki még késő aggkorában is dolgozott; bemutatott analitikus geometriai tételét a kör és gömb egyenletéről 79 éves korában közölte. A róla alkotott kép nem lenne teljes, ha meg nem emlékeznénk tudományos életünkben betöltött szerepéről, szervező képességeiről és a kiváló tanárról. Nagy tekintélyét ismételten felhasználta arra, hogy a mindinkább terpeszkedő fasizmus tudományellenes intézkedései ellen tiltakozzék, pl. az ún. ,,zsidótörvény'' ellen a magyar értelmiség színe-java tiltakozott, a nyilatkozat aláírói között találjuk Rados Gusztávot is. Mint a Matematikai és Fizikai Társulat elnöke szinte tüntetésképpen választtatta meg a mind jobban térthódító fasizmus elől külföldre távozott két fiatal elsőrangú magyar matematikust (Radó Tibort az Ohio állambeli Columbus egyetem és Neumann Jánost, a hírneves princetoni egyetem világhírű tanárait) a Társulat tiszteletbeli tagjainak.
Szólnom kell még a nagyszerű tanárról. Említettem már, hogy egész pályafutása alatt mint a műegyetem tanára működött. Világos, jól érthető előadása a hallgatóság sorában igen kedvelt volt, és nagyban hozzájárult a matematika népszerűsítéséhez a magyar mérnöki karban, egyben jelentékenyen emelte a mérnökök tudományos színvonalát. A mai idősebb mérnöknemzedék (az építészek és vegyészek kivételével) mind az ő tanítványa volt. Az idősebb középiskolai matematikai tanárok is tőle tanulták a számelmélet és a funkcionális algebra elemeit. Meg vagyok győződve, hogy minden volt tanítványa ‐ számuk tízezrekre rúg ‐ szeretettel gondol rá.
Rados Gusztávban tehát az akkor virágzóban levő matematikai élet egyik kiváló egyéniségével ismerkedtünk meg.

¹RADOS G.: Adalék a szabályos sokszögek elméletéhez. Math. és Termtud. Ért. 22., 1904. 66‐68 old. ‐ Beitrag zur Theorie der regul

ä

ren Vielecke. Math. u. natw. Berichte aus Ungarn, 22. 1904. 1‐12. old. ‐ Ugyanez franciául: Rados G.: Contribution a la théorie des polygones réguliers. Rendiconti del Circolo Matematico di Palermo. 49., 1925. 1‐4. old.
A tételt azonban már ezen közlései előtt ismerte. E sorok írója az 1900/01 tanévben hallgatta Rados számelméleti előadását, melyben a csillagsokszögekről szóló, a szövegben tárgyalt tételeket is előadta.

²RADOS G. Adalék a szabályos sokszögek elméletéhez. Math. és Termtud. Ért. 41., 1924., 109‐114. old. ‐ Contribution a la théorie des polygones réguliers. Rendiconti del Circolo Matematico di Palermo 49., 1925. 1‐4. old. főleg a 3. és 4. oldalán.

³RADOS G.: Egy minimum-probléma elemi tárgyalása. Math. és Phys. Lapok 2., 1893. 109‐117. old. ‐ Ld. még a következő cikket: BERKES JENŐ: A talpponti háromszögről. Lapunk XII., 1956. 66‐72. old.

⁴RADOS G.: Három pontjával meghatározott kör és négy pontjával meghatározott gömb egyenletéről. Mat. Termtud. Ért. 60., 1941., 1‐8. old.

⁵RADOS G.: Egész együtthatós trigonometrikus polynomok egy nevezetes tulajdonsága. Math. és Phys. Lapok 28., 1922., 27‐29. old. ‐ Ugyanez franciául: Sur une propriété remarquable des polynomes trigonométriques a coefficients entiers. Rendiconti del Corcolo Matematico di Palermo. 47., 1923., 62‐64. old.