Kezdőlap


Cím:	Egy görbe származtatása két különböző módon
Szerző(k):	Horvay Katalin
Füzet:	1957/január, 3 - 6. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Olyan görbéről lesz szó, amelyet bizonyos tükrökről visszaverődő fénysugarak alakítanak ki. Tudjuk, hogy sík, tükröző felületre eső fény úgy verődik vissza, hogy a beeső és visszaverődő sugár egyenlő szöget zár be a beesési merőlegessel. Beesési merőlegesen a beesés pontjában a tükör síkjára emelt merőlegest értjük. Ez, továbbá a beeső és visszavert sugár egy síkban van. Ha a tükröző felület görbült, akkor a visszaverődés úgy történik, mintha a beesés pontjában a tükröző felülethez fektetett érintő síkon jönne létre a visszaverődés. Tekintsünk egy gömbtükröt, éspedig egy félgömb belső felülete legyen a tükröző felület. A beesési merőleges most mindig a fénysugár beesési pontjához tartozó gömbi sugár lesz. Legyen a fénysugár a fél gömb tengelyével párhuzamos (a félgömböt határoló főkör síkjára merőleges). A visszavert fénysugár a beeső fénysugárhoz tartozó főkör síkjában lesz. Ezt a főkört, a beeső és visszavert fénysugarat rajzoltuk meg az 1. ábrán.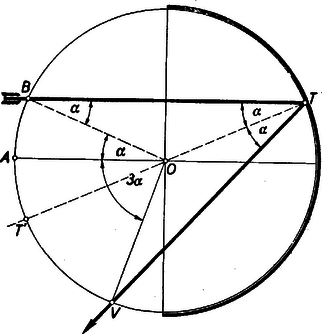

1. ábra

A fénysugár beesési pontja

T

, a beesési merőleges

O T

. A félgömb tengelye az

A

, a beeső fénysugár a

B

, a visszavert fénysugár a

V

, a beesési merőleges a

T'

pontban metszi a főkör nem tükröző részét. Mivel a beeső és visszaverődő sugár ugyanazt az

α

szöget zárja be, az

O T

-vel, azért

T B = T V

, és

T' B = T' V

, továbbá a kerületi szögek és az ugyanazon íven nyugvó középponti szögek közötti összefüggésből adódik, hogy az

\hat{A B}

ívhez tartozó középponti szög

α

, az

\hat{A V}

ívhez tartozó középponti szög

3 α

.
Vegyük most ezen főkör síkjában a tengellyel párhuzamos fénysugarak összességét, és nézzük meg, hogyan helyezkednek el a visszavert fénysugarak (2. ábra).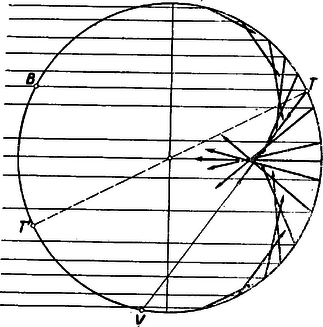

2. ábra

A visszavert fénysugarak szerkesztésénél a

T B = T V

, ill.

T' B = T' V

tulajdonságokat használtuk fel. (Mindig a rövidebb szakaszt ajánlatos a szerkesztésnél felhasználni, mert ez ad kevésbé hegyes metszést, tehát pontosabb metszéspontot.) Így a

V_{1}

V_{2}

...

pontok, és ezzel együtt a visszavert sugarak is könnyen szerkeszthetők. Már ezen néhány megszerkesztett visszavert sugár is egészen szépen mutatja, hogy a visszavert sugarak egy görbét burkolnak. A visszavert sugarak érintői egy görbének. A görbét sokkal jobban ismernők, ha minden megszerkesztett érintő érintési pontját is megszerkesztenők.
A 3. ábra szemléltet egy görbét, és annak

E

pontbeli

t

érintőjét.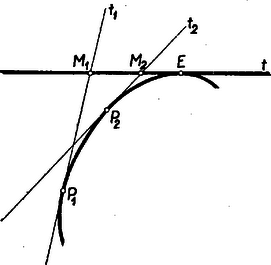

3. ábra

Szerepel az ábrán a

P_{1}

ponthoz tartozó

t_{1}

érintő is. A

t_{1}

és

t

metszéspontját

M_{1}

-gyel jelöltük. Vegyünk fel a görbén a

P_{1}

és

E

pont között egy

P_{2}

pontot, és a

P_{2}

-höz tartozó

t_{2}

érintőt. A

t_{2}

t

érintőt

M_{2}

pontban metszi. Általában, ha

P_{1}

elég közel van az

E

ponthoz, az

M_{2}

pont az

M_{1}

és az

E

közé esik. Ha így az

E

-hez egyre közelebb vesszük fel a

P_{3}

P_{4}

...

pontokat, a hozzájuk tartozó

t_{3}

t_{4}

...

érintőknek

t

-vel való

M_{3}

M_{4}

...

metszéspontjai egyre közelebb jutnak az

E

-hez.
Ezt vegyük figyelembe előbbi feladatunknál. Szerkesszük meg a burkolt görbe két érintőjét, vagyis két visszavert sugarat (4. ábra).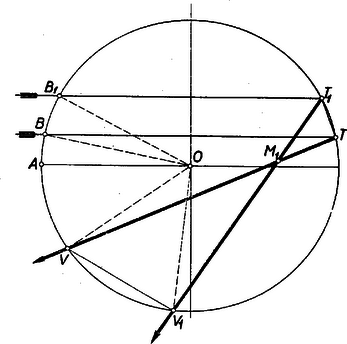

4. ábra

\begin{matrix} M_{1} T_{1} T_{△} \sim M_{1} V V_{1 △}, \end{matrix}

mert a kerületi szögek tétele értelmében szögeik egyenlők.
Mint fentebb láttuk,

{\hat{A V}}_{1} = 3 {\hat{A B}}_{1}

\hat{A V} = 3 \hat{A B}

, és így a különbséget képezve

{\hat{V V}}_{1} = 3 {\hat{B B}}_{1}

. De a szerkesztés alapján

{\hat{B B}}_{1} = {\hat{T T}}_{1}

, tehát

\begin{matrix} {\hat{V V}}_{1} = 3 {\hat{T T}}_{1} . \end{matrix}

Közeledjünk

B_{1}

ponttal (mindig a körön maradva) a

B

ponthoz, akkor

T_{1}

T

-hez,

V_{1}

pedig a

V

-hez közeledik,

M_{1}

pedig közeledik a

T V

érintő

E

érintési pontjához. Minél jobban megközelíti a

T_{1}

T

-t,

V_{1}

V

-t, annál jobban megközelíti¹ a

T_{1} T

és

V_{1} V

húrok aránya a

\hat{T_{1} T}

és

\hat{V_{1} V}

ívekét, amely ‐ mint láttuk ‐

1 : 3

. Mivel hasonló háromszögekről van szó, azért az előbbi arány megegyezik

T M_{1} : M_{1} V

aránnyal. Így, míg

B_{1}

közeledik

B

-hez, az

M_{1}

pont egyre jobban megközelíti az érintő

T V

szakaszának

T

-től számított első negyedelő pontját. Azt kell tehát mondanunk, hogy a visszavert

T V

sugáron az

E

érintési pontra nézve

T E : E V = 1 : 3

. Ennek alapján könnyen megszerkeszthetők a visszavert sugarak által burkolt görbe egyes pontjai is (5. ábra).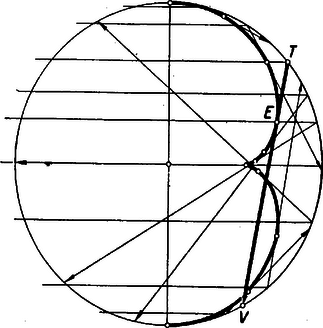

5. ábra

Látszólag egész más kérdést fogunk most tárgyalni, de majd észrevesszük az előbbiekkel való összefüggést.
Tekintsünk egy

r

sugarú kört és egy, azt kívülről érintő,

r / 2

sugarú kört. Szemeljük ki a két kör

P

érintkezési pontját. Gördítsük az

r / 2

sugarú kört az

r

sugarú körön, s nézzük meg, hogy milyen görbét ír le közben a

P

pont (6. ábra).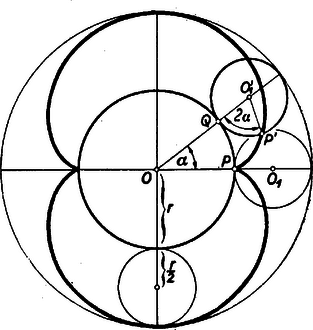

6. ábra

r / 2

sugarú kör

O_{1}

középpontja kört ír le mozgás közben. Egy pillanatnyi helyzetben

O'_{1}

helyre került. Akkor

α

szöggel fordult el az

O

körül. Az

r / 2

sugarú kör azonban nem csúszik, hanem gördül. Gördülés közben a

P

pont a

P'

helyzetbe került, ahol

\hat{Q P} = \hat{Q P'}

. Félakkora sugarú körben viszont ugyanakkora ívhez kétszer akkora középponti szög tartozik. Amíg tehát az

r / 2

sugarú kör középpontja

α

szöggel fordul el az

O

körül, az

r / 2

sugarú kör

2 α

szöggel fordul el a középpontja körül. Tehát a

P'

pont az az

O'_{1}

középpontú

r / 2

sugarú körön az

O O'_{1} P' ∢ = 2 α

felhasználásával szerkeszthető.
A

P

pont egy pillanatnyi helyzetét (

P'

) még egyszer lerajzoltuk a 7. ábrán.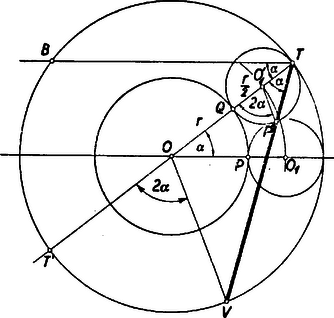

7. ábra

B T

egyenest az

O P

egyenessel párhuzamosan húztuk. Így a

B T O ∢ = α

, mint váltószög. A

P' T O ∢

szintén

α

, a kerületi szögek tétele alapján. Ez viszont azt jelenti, hogy a

B T

fénysugár a

2 r

sugarú,

O

középpontú gömbtükörről

T P'

egyenesben verődne vissza.
Az

O'_{1} P'

és

O V

egyenesek párhuzamosak, mert mindkettő a

T T'

egyenes ugyanazon irányával

2 α

szöget zár be a kerületi szögek tétele szerint. Ebből adódik, hogy

\begin{matrix} O V T_{△} \sim O'_{1} P' T_{△}, \end{matrix}

és így

\begin{matrix} T P' : T V = T O'_{1} : T O = \frac{r}{2} : 2 r = 1 : 4. \end{matrix}

Az az eredmény adódott tehát, ha az előbb vizsgált görbével összevetjük, hogy a

P

pont által leírt görbe azonos a

B T

-vel párhuzamosan beeső fénysugaraknak a

2 r

sugarú körről visszavert fénysugarai által burkolt görbével.
Ime, ugyanazt a görbét két különböző módon származtattuk.
A gömbtükör tengelyével párhuzamos összes sugarakat tekintve, a visszavert sugarak minden egyes főkör síkjában burkolnak ilyen görbét, vagyis a visszaverődő sugarak összessége egy forgásfelületet burkol, amely a tárgyalt görbének a tükör tengelye körül forgásából keletkezik (és egy alma felső felületéhez hasonlít).
Ha félkörhenger belső felülete a tükröző felület, és a fénysugarak iránya a henger tengelyére merőleges, akkor a visszavert sugarak egy ugyancsak hengerszerű felületet burkolnak, amelynek keresztmetszete az itt tárgyalt görbe. Hasonló görbe alakul ki fényesen egy üres csésze fenekén, ha ferdén belesüt a nap. Itt a csésze oldala a tükröző hengerfelület, mivel azonban a sugarak nem a tengelyre merőlegesen érkeznek, azért a csészében látható görbe is csak hasonlít az itt tárgyalthoz. (Gyakran a fenti görbe csúcsa helyén kis hurok alakul ki.)
A második származtatási móddal kapcsolatban a következőket kívánjuk még hozzáfűzni. Ha egy rögzített

f

síkgörbén ‐ annak síkjában ‐ egy

g

síkgörbe gördül, akkor a

g

görbe síkjának minden pontja egy görbét ír le, melynek neve ruletta. Ha

f

egyenes vagy kör, és

g

kör, akkor ciklois keletkezik, mégpedig epiciklois, ha a

g

kör az

f

körön kívül gördül, és hipociklois, ha

g

f

körön belül gördül. Azonkívül hurkolt, csúcspontos és nyújtott cikloisról beszélünk aszerint, amint a

P

leíró pont a

g

körön kívül, rajta, ill. belül van. Eszerint az itt tárgyalt görbe egy kétágú csúcspontos epiciklois.

¹Az itt következő meggondolás csak heurisztikus, de a függvénytan elemei segítségével szigorú matematikai bizonyítássá egészíthető ki.