Cím: Az 1956. évi Arany Dániel matematikai tanulóverseny (3., befejező közlemény)
Füzet: 1956/november, 74 - 79. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alább közöljük a haladók (II. osztályosok) versenyén kitűzött feladatok megoldásait.

 

I. forduló
 

1. feladat. Valamely iskolában az év elején a leánytanulók létszáma 51-gyel kisebb, mint a fiúké. Év közben kimaradt 19 fiú és 41 lány, aminek következtében a év végén a lányok létszáma az összlétszám százalékaiban kifejezve 4%-kal kisebb, mint az év elején volt. Hány fiú- és hány lánytanuló volt az év elején ?
 

Megoldás: Jelöljük x-szel a lányok számát az év elején. Ekkor a lányok és fiúk száma az év elején, illetőleg év végén x és x+51, illetőleg x-41 és x+32. A lányok számát az összlétszám százalékában kifejezve a feladat feltétele a következő egyenletre vezet:
100x2x+51=100(x-41)2x-9+4.

Az egyenletet 4-gyel osztva, a törteket eltávolítva és 0-ra redukálva, nyerjük, hogy gyökei megegyeznek a
-4x2+466x+52734=0,
vagy a
2x2-233x-26367=0
egyenlet gyökeivel, feltéve, hagy utóbbiak különböznek az eltávolított nevezők gyökeitől. A nyert egyenletnek egy pozitív és egy negatív gyöke van, amelyek közül csak az előbbi felel meg a feladat feltételeinek, tehát a lányok száma az év elején
x=233+54289+2109394=233+5154=187,
(ami valóban nem gyöke az eltávolított nevezőknek), a fiúk száma pedig 238 volt. (A lányok év elején az összes tanulók 44 %-át, az év végén a tanulók 40 %-át tették ki.)
 

2. feladat. Bizonyítsuk be, hogy
n6-n2
osztható 60-nal, ha n természetes szám.
 

Megoldás: A vizsgálandó kifejezés
n2(n4-1)=(n2-1)n2(n2+1)=(n-1)n(n+1)n(n2+1).

Ha n egész szám, akkor itt az első három tényező három szomszédos egész szám. Ezek közül valamelyik osztható 3-mal.
Ha n páratlan, akkor az első és harmadik tényező, ha páros, akkor a második és negyedik osztható 2-vel, a szorzat tehát osztható 4-gyel.
Az első három tényező közül valamelyik osztható 5-tel is, ha n osztható 5-tel, vagy szomszédos egy 5-tel osztható számmal. Ha viszont n egy 5-tel osztható szám második szomszédja: n=5k+2, akkor az utolsó tényező
n2+1=25k2+20k+4+1=5(5k2+4k+1)
osztható 5-tel.
Az n6-n2 kifejezés tehát minden egész n-re osztható 3-mal, 4-gyel és 5-tel. Ebből következik, hogy 60-nal is osztható,* mert minden szám 60-nal osztva
60h+m
alakban írható, ahol 0≤m≤59 a maradék. Mivel az első tag osztható 3-mal, 4-gyel és 5-tel, az összeg csak úgy lehet mindhárom számmal osztható, ha m is osztható mind a hárommal.
Csak a 0-ra és 5-re végződő számok oszthatók 5-tel és ezek közül is csak 0-ra végződők lehetnek 4-gyel oszthatók, tehát m lehetséges értéke csak
0,10,20,30,40,50.
Ezek közül csak 0 és 30 osztható 3-mal, de az utóbbi nem osztható 4-gyel, tehát m=0 és így minden 3-mal, 4-gyel és 5-tel osztható szám osztható 60-nal is. Ezzel bizonyítottuk a tétel állítását.
 

Megjegyzés. Az, hogy a 3-mal, 4-gyel és 5-tel való oszthatóságtól a szorzatukkal 60-nal való oszthatóságra következtethetünk, azon múlik, hogy e három szám közül semelyik kettőnek nincs 1-nél nagyobb közös osztója. Nem volna nehéz a kifejezés 4-gyel, 5-tel és 6-tal való oszthatóságát kimutatni, ebből sem következtethetnénk 4⋅5⋅6=120-szal való oszthatóságra, amint hogy a kifejezés n=2-re 60-at ad és ez mindjárt nem osztható 120-szal. Ebbe a hibába többen beleestek, hogy két számmal való oszthatóságból a szorzatukkal való oszthatóságra következtettek, nem törődve a tényezők közös osztóival.
 

3. feladat. Legyen az ABCD trapéz érintőnégyszög. (AB∥CD). A beírt körhöz az átellenes A és C csúcsból húzott érintőszakaszok hossza legyen u ill. v. Bizonyítandó, hogy
u⋅CD=v⋅AB.

I. megoldás: Jelöljük az AB és CD oldalak hosszát a-val és c-vel, az AB, BC, CD, DA oldalakon levő érintési pontokat P, Q, R, S-sel. Bocsássunk merőlegest a C és D pontokból az AB egyenesre (1. ábra).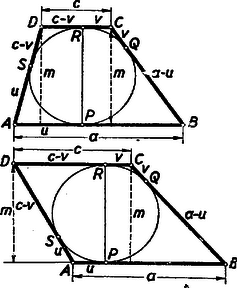
 
 
1. ábra
 

Két derékszögű háromszög keletkezik, melyek átfogója a BC, ill. DA oldal, egyik befogója a trapéz m magasságával, másik pedig a BP és CR, illetőleg a DR és AP érintőszakaszok különbségének abszolút értékével egyenlő. Mivel a körhöz egy pontból húzott érintőszakaszok egyenlők, így
BP=BQ=a-u,DR=DS=c-v,
tehát a derékszögű háromszögekre Pythagoras tételét alkalmazva
(a-u+v)2=m2+|a-u-v|2,(u+c-v)2=m2+|u-(c-v)|2.



Miután egy számnak és negatívjának a négyzete megegyezik, az abszolútérték-jeleket elhagyhatjuk. A második egyenletet az elsőből levonva az
[a-(u-v)]2-[c+(u-v)]2=[a-(u+v)]2-[(u+v)-c]2
összefüggéshez jutunk. Ebből a zárójelek felbontása és rendezés után kapjuk, hogy
4av=4cu,
ami egyenértékű a bizonyítandó összefüggéssel.
 

II. megoldás: A beírt kör O középpontja a trapéz szögfelezőinek metszéspontja. Mivel a trapéz B-nél és C-nél levő szögeinek összege 180∘, azért a BOC háromszög B-nél és C-nél levő szögeinek összege 90∘, és így a háromszög O-nál derékszögű (2. ábra).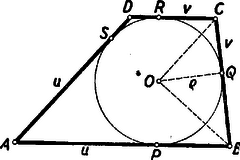
 
 
2. ábra
 

Az átfogóra bocsátott magasság a beírt kör sugara, ϱ. Így a derékszögű háromszögre vonatkozó középarányossági tételek szerint
ϱ2=BQ⋅CQ.
Hasonlóan adódik a DOA háromszögből, hogy
ϱ2=DS⋅AS,
tehát a jobb oldalak is egyenlők. Felhasználva ezt és azt, hogy körhöz egy pontból húzott érintőszakaszok egyenlők, nyerjük, hogy
u⋅CD=AS(DR+RC)=AS(DS+v)=AS⋅DS+AS⋅v=BQ⋅CQ++AS⋅v=BP⋅v+AP⋅v=AB⋅v,


és ezt kellett bizonyítanunk.
 

III. megoldás: Az állítás nyilvánvaló, ha BC∥DA, ezért feltehetjük, hogy a BC és DA oldalaknak mondjuk a C-n és D-n túli meghosszabbításai metszik egymást egy E pontban. Érintse a trapézba írt kör a párhuzamos oldalakat a P és R pontban, a CDE háromszögbe írt kör pedig a CD oldalt az R' pontban (3. ábra).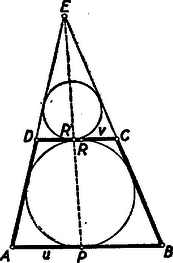
 
 
3. ábra
 

A trapézba írt kör a CDE háromszögnek hozzáírt köre, és egyben az ABE háromszögnek beírt köre. Ismeretes, a hozzáírt és beírt körre nézve a
CR=DR'
összefüggés.
Mivel az ABE és DCE háromszögek hasonlók és R' és P e hasonlóságnál egymásnak megfelelő pontok, így fennáll az
ABCD=APDR'=APCR=uv
összefüggés, ami a bizonyítandó állításnak csak átrendezett alakja.
 

Megjegyzések. Sokan abból kiindulva bizonyították a tételt, hogy a párhuzamos oldalak érintési pontjait összekötő egyenes átmegy az átlók metszéspontján, vagy, hogy érintőnégyszögben az átlók és a szemközti oldalakon levő érintési pontokat összekötő egyenesek egy ponton mennek keresztül. Ez az állítás ugyan igaz, de bizonyítása sokkal nehezebb, mint a feladat állításáé. Mások viszont abból a hamis állításból indultak ki, mely szerint két négyszög hasonló volna, ha megfelelő szögeik egyenlők.
 

II. forduló
 

1. feladat. Négy egész szám összege 36. Egy bizonyos n egész számot hozzáadva az első számhoz; n-net kivonva a második számból; n-nel szorozva a harmadik számot, és n-net osztva a negyediket, egyenlő eredményre jutunk. Melyik ez a négy szám, és mekkora n ?
 

Megoldás: A négy számot x, y, z, u-val jelölve feltétel szerint
x+y+z+u=36(1)x+n=y-n=z⋅n=un.(2)


Célszerű (2)-ből azzal a két ismeretlennel fejezni ki a többit, amelyikkel ez csupán összeadás, kivonás, és szorzás segítségével sikerül; ez a z és n lesz, melyek szorzata szerepel (2)-ben:
x=zn-n,y=zn+n,u=zn2,
és (1) bal oldalába beírva e kifejezéseket, a
2zn+z+zn2=z(n+1)2=36
egyenletet kapjuk. Innen (n+1)2 csak 1, 4, 9 vagy 36 lehet. Az ismeretlenek lehetséges értékeit az alábbi táblázatban tüntettük fel (tekintetbe véve, hogy az n=0 értéket ki kell zárnunk).
(n+1)214936n...-21-32-45-7z...36994411x...-708-246-1200y...-7410-3010-2010-14u...14498116642549

Megjegyzés. Ha más két ismeretlennel fejezzük ki a többit, akkor is egész hasonlóan történhet a megoldás, csak nehezebbé válhat a szorzattá alakítás lehetőségének megtalálása. Emellett külön kell diszkutálni nevezőbe kerülő kifejezések eltűnésének az esetét is.
 

2. feladat. Egy hatszög minden második szöge 120∘-os, és két-két 120∘-os szöget bezáró oldala egyenlő. Bizonyítandó, hogy a 120∘-os szögek csúcsai szabályos háromszöget alkotnak.
 

I. megoldás: Legyenek az 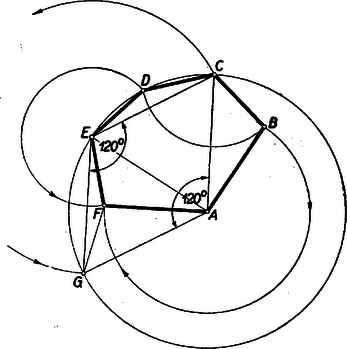ABCDEF hatszög A, C és E csúcsoknál levő szögei 120∘-osak. Ekkor a másik három szög összege is 360∘; mert a hatszög szögeinek összege 720∘. Így az ABC háromszöget A körül elforgatva, míg AB a vele egyenlő AF oldalra kerül és hasonlóan a CDE háromszöget E körül ED oldalával EF-re forgatva, a BC és DC oldalak egy egyenesre fognak kerülni (4. ábra), és mivel a két oldal egyenlő, a C csúcs a két forgatásnál ugyanabba a G pontba kerül.
 
 
4. ábra
 

A keletkező AEG háromszög az AEC háromszög tükörképe az AE egyenesre nézve. Az elforgatás folytán keletkezett CAG és CEG szögek 120∘-osak, s így az AE szimmetriatengely az AC és EC oldalakkal 60∘-os szöget zár be, az ACE háromszög tehát szabályos.
 

II. megoldás: a) Az állítást konvex hatszögre igazoljuk. Az előző megoldás jelöléseit használva rajzoljunk 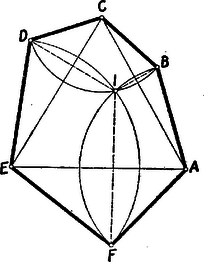A középpontú körívet F-en és B-n át a (120∘-os) FAB szög szárai közé és hasonlóan C középpontú kör a BCD szög szárai közé B-n és D-n át. A két körívről az FB, ill. BD szakasz 120∘ alatt látszik, mert a látószögek 240∘-os középponti szöghöz tartozó kerületi szögek. (5. ábra).
 
 
5. ábra
 

Belátjuk, hogy a két körív metszi egymást. A D pont az FAB120∘-os szögtérben van, mert a hatszög konvex, továbbá az FB köríven kívül, mert különben az FDB szög legalább 120∘-os volna. Mivel a BCD és DEF egyenlőszárú háromszögek szárai közti szög 120∘, így ezeknek a D-nél levő szárai 30∘-osak, tehát a hatszög D-nél levő szöge 180∘-nál nagyobb volna, de ez lehetetlen, mert a hatszög konvex. Ugyanígy következik, hogy az F pont a BCD120∘-os szögtérben van, a BD köríven kívül. A BD körív az FAB körcikk belsejébe indul a B pontból, mert az ABC szög a hatszög konvex volta miatt 180∘-nál kisebb. Így a két körív valóban metszi egymást egy I pontban. Ez a pont B tükörképe az AC egyenesre.
Az I pontból, mint láttuk, az FB és BD szakasz 120∘-os szög alatt látszik, s így ugyanakkora szögben látszik a DF szakasz vagyis az E középpontú, D-n és F-en áthaladó kisebb körív is átmegy I-n. Ebből következik, hogy az I pont D-nek is tükörképe a CE egyenesre és F-nek is tükörképe az EA egyenesre.
Az ACE háromszög oldalai a bizonyítottak szerint merőlegesek, az egymással 120∘-os szöget bezáró, IB, ID és IF szakaszokra s így szabályos háromszöget alkotnak.
b) Ha a hatszögben pl. a 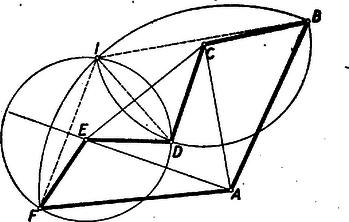D csúcsnál levő szög 180∘-nál nagyobb, akkor D az FAB körcikkben van, s így a BD és DF körívek meghosszabbítása metszi az FB ívet egy közös I pontban (6. ábra).
 
 
6. ábra
 

A bizonyítás ez esetben az előbbihez teljesen hasonló módon fejezhető be.
 

3. feladat. Hány téglalap látható a sakktáblán ? Ezek közül hány négyzet ?
 

Megoldás. Ha meghosszabbítjuk egy téglalap függőleges oldalait, kapunk a sakktáblán egy függőleges sávot. Hasonlóan a vízszintes oldalak egy vízszintes sávot határoznak meg. Fordítva, ha megadunk egy sakktáblamezőket elválasztó egyenesek határolta függőleges sávot és egy vízszinteset a sakktáblán, ezek egyértelműen meghatároznak egy téglalapot (7. ábra).
 
 
7. ábra
 

Így az összes téglalapok száma a függőleges és a vízszintes sávok számának szorzata.
Világos, hogy ugyanannyi a függőleges és a vízszintes sávok száma, tehát elegendő pl. az előbbieket összeszámolni. A sakktábla mezőit 9 függőleges egyenes határolja.
Ezek közül 9-féleképpen választhatjuk ki az első határvonalat, és 8-féleképpen a maradék közül a másodikat. Így azonban minden sávot kétszer, kapunk meg, tehát a függőleges sávok száma
9⋅82=36.
Ugyanannyi a vízszintes sávok száma is, tehát az összes téglalapok száma
362=1296.

Ezek között annyi négyzet van, ahányféleképpen ugyanolyan szélességű függőleges és vízszintes sávot párosíthatunk.
Egy h szélességű függőleges sáv baloldali határa nem lehet az utolsó h függőleges egyenes egyike sem, tehát a h szélességű sávok száma 9-h, ennyi a vízszinteseké is, s így (9-h)2 olyan négyzet van, amely h mező szélességű. Tehát a négyzetek száma (h=1,2,...,8) 82+72+62+52+42+32+22+12=204.
*Hivatkozhatnánk egyszerűen arra a tételre, hogy ha egy egész szám osztható olyan egész számokkal, amelyek páronként relatív prímek egymáshoz, akkor osztható ezek szorzatával is. A következő meggondolás azonban azt mutatja, hogy ezt konkrétan adott számok esetén könnyű közvetlenül igazolni.