Kezdőlap


Cím:	Az 1956. évi Arany Dániel matematikai tanulóverseny (2. közlemény)
Füzet:	1956/október, 33 - 41. oldal	PDF \| MathML
Témakör(ök):	Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alábbiakban közöljük a kezdők (I. osztályosok) versenyén kitűzött feladatok megoldásait.
Az I. forduló feladatai:

1. feladat. Mennyi a %-os alkoholt kell hozzátöltenünk b liter c %-os alkoholhoz, hogy d %-os alkoholt kapjunk ?

Megoldás: Nyilvánvalóan csak akkor várható megoldása a feladatnak, ha

d

a

és

c

közé eső érték. Általában

p

%-os alkohol azt jelenti, hogy

m

liter oldatban

\begin{matrix} \frac{p \cdot m}{100} \end{matrix}

liter alkohol van. Így, ha a

b

liter

c

% alkoholhoz

x

liter

a

%-os alkoholt adva, a keletkezett

b + x

liter

d

%-os lesz, ekkor az alkoholtartalmat kétféleképpen kiszámítva

\begin{matrix} \frac{b c}{100} + \frac{a x}{100} = \frac{(b + x) d}{100} . \end{matrix}

Innen, ha

d \neq a

\begin{matrix} x = b \frac{d - c}{a - d} . \end{matrix}

x

-re akkor ad pozitív értéket, ha

a - b

és

d - c

egyező előjelű, ami éppen azt jelenti, hogy

d

a

és

c

közé esik.

2. feladat. Szerkesszünk háromszöget, ha ismeretes a kerülete (k), egyik oldala (c), és a másik két oldallal szemközti szögek különbsége

(α - β)

Megoldás: Jelöljük az adott szögkülönbséget

δ

-val. Ha a

c

oldal és a kerület adott, akkor ismert a másik két oldal összege

a + b

is. A szerkeszthetőséghez természetesen szükséges, hogy

\begin{matrix} a + b = k - c > c, \end{matrix}

azaz

\begin{matrix} 2 c < k \end{matrix}

legyen.
Forgassuk rá egy tetszésszerinti

A B C

háromszögben pl. a

B C = a

oldal meghosszabbítására a

C A' = b

oldalt (1. ábra).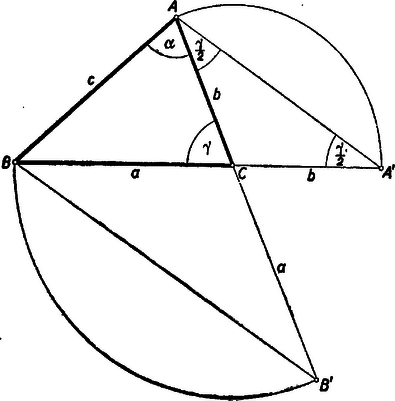

1. ábra

A keletkezett

A C A'

egyenlő szárú háromszög

C

csúcsánál levő külső szöge az

A B C

háromszög

γ

szöge, így az

A A'

alapon fekvő szögek

\frac{γ}{2}

nagyságúak.
Számítsuk ki a keletkező

A B A'

háromszögben az

A

-nál levő szöget:

\begin{matrix} A' A B ∢ = α + \frac{γ}{2} = α + \frac{180^{\circ} - (α + β)}{2} = 90^{\circ} + \frac{α - β}{2} = 90^{\circ} + \frac{δ}{2} . \end{matrix}

A A' B

háromszögben ismert tehát két oldal és a nagyobbikkal szemközti szög, így ez egyértelműen megszerkeszthető. Az

A A'

oldal felező merőlegese metszi ki az

A' B

oldalból a

C

pontot (2. ábra).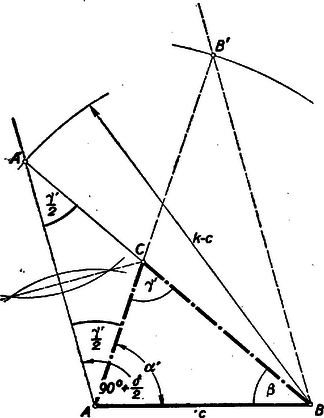

2. ábra

Ez a

B A'

oldal belsejére esik, mert az

A' A B

szög tompaszög.
A keletkezett

A B C

háromszög kielégíti a feltételeket, mert ‐ szögeit

α'

β'

γ'

-vel jelölve ‐ az

A C A'

háromszög szerkesztés szerint egyenlő szárú, így az alapon fekvő szögei feleakkorák, mint a

C

csúcsnál levő külső szög,

γ'

. Ezért

\begin{matrix} α' - β' = 90^{\circ} + \frac{δ}{2} - \frac{γ'}{2} - β' = 90^{\circ} + \frac{δ}{2} - \frac{180^{\circ} - (α' + β')}{2} - β' = \frac{δ}{2} + \frac{α' - β'}{2} . \end{matrix}

Innen

\begin{matrix} α' - β' = δ, \end{matrix}

másrészt a

C

csúcsból induló oldalak összege

\begin{matrix} A C + C B = A' C + C B = A' B, \end{matrix}

szintén az előírt

k - c

érték.

Megjegyzés: Az

A A'

oldal a

C

csúcsból induló szögfelezővel párhuzamos, és ha az

A C

oldal meghosszabbítására mérjük rá a

C B

-vel egyenlő

C B'

távolságot, akkor ugyanúgy

B B'

is párhuzamos a szögfelezővel. (1. ábra). A szerkesztés ennek alapján úgy is befejezhető, hogy az

A A' B

háromszög után ugyanarra az

A B

oldalra megszerkesztjük az

A B B'

háromszöget

(B B' | | A A'

és

A B' = k - c)

is. Ekkor

C

A B'

és

A' B

oldalak metszéspontjaként adódik (2. ábra).

3. feladat. Vonjuk le egy egész szám utolsó jegyének kétszeresét az utolsó jegy elhagyásával kapott számból (ha az egész szám egyjegyű, akkor

0

-ból). Igazoljuk, hogy ha az eredmény osztható

7

-tel, akkor az eredeti szám is mindig osztható

7

-tel, ha viszont az eredmény nem osztható

7

-tel, akkor az eredeti szám sem lehet

7

-tel osztható.

Megoldás: Az adott egész számot

n

-nel, utolsó számjegyét

b

-vel, az ennek elhagyásával keletkező számot

a

-val jelölve (

0 \leq b \leq 9

a \geq 0

) a feladat előírása szerint az

\begin{matrix} n = 10 a + b \end{matrix}

számhoz a

\begin{matrix} d = a - 2 b \end{matrix}

számot kell kiszámítani. Innen kiküszöbölhetjük pl.

b

-t úgy, hogy

d

-t hozzáadjuk

n

kétszereséhez:

\begin{matrix} 2 n + d = 21 a . \end{matrix}

A jobboldal osztható 7-tel, azért a baloldali összegnek is oszthatónak kell lennie 7-tel. Ebből következik, hogy ha valamely tag osztható 7-tel, akkor a másik is. Ha tehát

d

osztható 7-tel, akkor

2 n

is osztható 7-tel, különben pedig nem.
Ebből továbbá következik a feladat állítása, mert tudjuk, hogy

2 n

akkor és csakis akkor osztható 7-tel, ha

n

osztható 7-tel. Világos, hogy ha

n

osztható 7-tel, akkor

2 n

is. Ha viszont

n

nem osztható 7-tel, akkor 1, 2, 3, 4, 5 vagy 6 maradékot ad, és a kétszerese ekkor rendre 2, 4, 6, 1, 3 illetőleg 5 maradékot ad, tehát szintén nem osztható 7-tel.

A II. forduló feladatai:

1. feladat. Bizonyítsuk be, hogy

\begin{matrix} (a^{2} + b^{2}) (c^{2} + d^{2}) \geq {(a c + b d)}^{2} \end{matrix}

bármilyen pozitív vagy negatív (esetleg

0

) számokat jelentsen a, b, c, d. Mikor érvényes az egyenlőség jele ?

Megoldás: Képezzük a két oldal különbségét

\begin{matrix} (a^{2} + b^{2}) (c^{2} + d^{2}) - {(a c + b d)}^{2} = a^{2} d^{2} + b^{2} c^{2} - 2 a b c d = {(a d - b c)}^{2} \geq 0, \end{matrix}

a

b

c

d

minden számbajövő értékére. Egyenlőség csak abban az esetben állhat fenn, ha

\begin{matrix} a d = b c . \end{matrix}

Megjegyzés. 1. A bizonyítás a következő azonosság levezetésével történt:

\begin{matrix} (a^{2} + b^{2}) (c^{2} + d^{2}) = {(a c + b d)}^{2} + {(a d - b c)}^{2} . \end{matrix}

Ebből az itt bizonyított egyenlőtlenség mellett egy számelméleti érdekesség is leolvasható: ha itt

a

b

c

d

egész számokat jelentenek, akkor az azonosság azt fejezi ki, hogy ha két egész szám kifejezhető két négyzetszám összegeként (

m = a^{2} + b^{2}

és

n = c^{2} + d^{2}

), akkor a szorzatuknak is megvan ez a tulajdonsága. Ez lényeges segítséget nyújt annak a kérdésnek vizsgálatában, hogy mely számok állíthatók elő két négyzetszám összegeként (lásd idevonatkozóan pl. Matematikai Versenytételek II. részben az 1938. évi 1. feladathoz fűzött jegyzetet).

2. Könnyen igazolható a felhasznált azonosság következő általánosítása:

(a_{1}^{2} + a_{2}^{2} + ... + a_{k}^{2}) (b_{1}^{2} + b_{2}^{2} + ... + b_{k}^{2}) - {(a_{1} b_{1} + a_{2} b_{2} ... + a_{k} b_{k})}^{2} = {(a_{1} b_{2} - a_{2} b_{1})}^{2} +

+ (a_{1} b_{3} - a_{3} b_{1}) + ... + (a_{1} b_{k} - a_{k} b_{1}) + {(a_{2} b_{3} - a_{3} b_{2})}^{2} + ... + (a_{k} b_{k - 1} - a_{k - 1} b_{k})

,

amiből leolvashatjuk az

\begin{matrix} (a_{1}^{2} + a_{2}^{2} + ... + a_{k}^{2}) (b_{1}^{2} + b_{2}^{2}) + ... + b_{k}^{2}) \geq {(a_{1} b_{1} + a_{2} b_{2} + ... + a_{k} b_{2})}^{2} \end{matrix}

nevezetes Cauchy-féle egyenlőtlenséget. Itt egyenlőség csak akkor állhat fenn, ha a

b_{i}

-k a megfelelő

a_{i}

-ből minden egyes

i

-re ugyanazon

c

számmal való szorzással keletkeznek.

2. feladat. Szerkesszünk háromszöget, ha adva van a kerülete

2

s, a beírt kör sugara

ϱ

, és szögeik szöge

α

I. megoldás: Legyenek a háromszög csúcsai

A

B

C

, az ezeknél fekvő szögek

α

β

γ

. Mivel a beírt kör

O

középpontját a szögfelező metszéspontja adja, ezért az

a = B C

oldal látószöge az

O

pontból (3. ábra)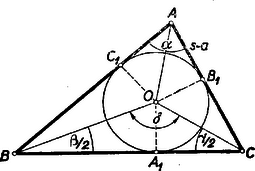

3. ábra

\begin{matrix} δ = 180^{\circ} - \frac{β}{2} - \frac{γ}{2} = 180^{\circ} - (\frac{α}{2} + \frac{β}{2} + \frac{γ}{2}) + \frac{α}{2} = 90^{\circ} + \frac{α}{2} . \end{matrix}

(1)

Ez a szög tehát

α

ismeretében megszerkeszthető. Azt is tudjuk, hogy

O

B C

oldaltól

ϱ

távolságra van, így a szerkesztés elvégezhető, ha

a

-t meg tudjuk szerkeszteni. Legyenek a beírt kör érintési pontjai a

B C

C A

A B

oldalon

A_{1}

B_{1}

C_{1}

, akkor ismeretes, hogy

\begin{matrix} A B_{1} = A C_{1} = s - B C = s - a . \end{matrix}

(2)

(Valóban a körhöz egy pontból húzott érintő egyenlő volta miatt

\begin{matrix} s = A B_{1} + B C_{1} + C A_{1} = A B_{1} + C A_{1} + A_{1} B = A B_{1} + a .) \end{matrix}

Ezzel a következő szerkesztéshez jutottunk: Rajzoljunk

\frac{α}{2}

nagyságú szöget, csúcspontját jelöljük

P

-vel (4. ábr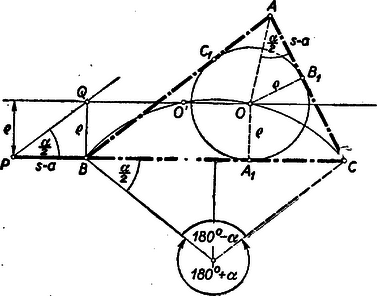a).

4. ábra

Húzzunk az egyik szárával párhuzamos egyenest

ϱ

távolságban, amely metszi a másik szárat egy

Q

pontban. Az előbbi szárra mérjük rá a

P

csúcstól a

P C = s

távolságot, a

Q

-ból

P C

-re bocsátott merőleges talppontja legyen

B

. Rajzoljuk meg azt a körívet, amelyből a

B C

szakasz

90^{\circ} + \frac{α}{2}

szög alatt látszik. Messe ez az először húzott párhuzamost

O

és

O'

pontokban. Rajzoljunk pl.

O

körül

ϱ

sugarú kört. Az ehhez

B

-ből és

C

-ből húzott érintők

A

metszéspontja lesz a keresett háromszög harmadik csúcspontja. (E két érintő szükségképpen metszi egymást, a

B C

ugyanazon az oldalán, amelyen a kör van. Ugyanis ezen érintőknek a

B C

szakasszal bezárt, a kör oldalán fekvő szögei

2 \cdot O B C ∢

, illetőleg

2 \cdot O C B ∢

, és e két szög összege

180^{\circ} - α

.)
Csak az így kapott háromszög felelhet meg a feladat feltételeinek, tehát nincs megoldása a feladatnak, ha a látókörív nem metszi a

ϱ

távolságban húzott párhuzamost.
Az

A B C

háromszög valóban megfelel a feltételeknek, mert beírt körének sugara

ϱ

, ennek a középpontjából a

B C

oldal

90 + \frac{α}{2}

szög alatt látszik, s így az

A

csúcsnál fekvő

α'

szögre (1) szerint

\begin{matrix} 90^{\circ} + \frac{α'}{2} = 90^{\circ} + \frac{α}{2}, α' = α . \end{matrix}

Végül a beírt kör érintési pontját a

C A

oldalon

B_{1}

-gyel jelölve, a szerkesztett háromszög

s'

kerületére (2) szerint

\begin{matrix} s' = A B_{1} + B C . \end{matrix}

De az

A O B_{1}

és

P Q B

derékszögű háromszögek egybevágók, mert

A

-nál, illetőleg

P

-nél fekvő hegyesszögük

\frac{α}{2}

, és az ezzel szemközti befogó mindkét háromszögben

ϱ

. Így

\begin{matrix} A B_{1} = P B . \end{matrix}

Ennélfogva

\begin{matrix} s' = P B + B C = s \end{matrix}

a szerkesztés szerint.
Ha

O

helyett az

O'

-ből kiindulva fejezzük be a szerkesztést, akkor

A B C

-vel egybevágó megoldást kapunk, mert

O

és

O'

szimmetrikus a

B C

szakaszt felező merőlegesére.

Megjegyzés. Legyen az

A B C

háromszög köré írt kör

A

-t nem tartalmazó

B C

ívének felezőpontja

D

(5. ábr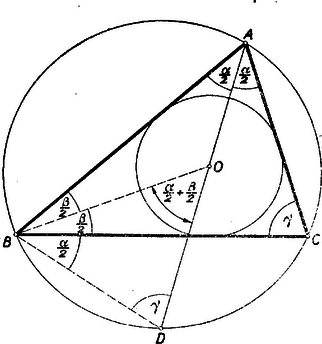a).

5. ábra

Tudjuk, hogy az

A

csúcsnál fekvő szög felezője átmegy

D

-n, és egyszerű szögszámítás adja, hogy a

B D O

háromszög egyenlő szárú:

D B = D O

. Így

B

O

és

C

egy

D

középpontú körön vannak. Ez éppen a fenti megoldásban használt látókörív.
Mivel

a

megszerkesztése után,

α

ismeretében a körülírt kör megszerkeszthető, így a

D

pont is. E körül

B

-n és

C

-n át körívet rajzolva, annak egyik metszéspontját a

B C

-től

ϱ

távolságra húzott párhuzamossal kössük össze

D

-vel. Ez metszi ki a körülírt körből

A

-t. Többen választották ezt a szerkesztési utat. Ehhez természetesen megfelelően kell módosítani annak bizonyítását is, hogy az

A B C

háromszög megfelel a feladat feltételeinek. (Lásd a jelen számban kitűzött 372. gyakorlatot.)

II. megoldás: Forgassuk le egy

A B C

háromszög oldalait pl. az

A B

oldal meghosszabbítására (6. ábra)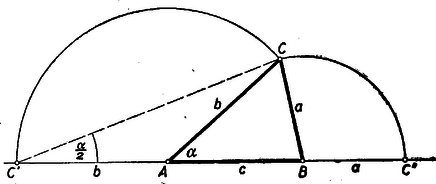

\begin{matrix} A C' = A C, B C' = B C . \end{matrix}

6. ábra

Ha az

A

csúcsnál levő szög

α

, akkor a

C A C'

háromszög egyenlő szárú voltából következik, hogy

\begin{matrix} C C' A ∢ = C C' C'' ∢ = \frac{α}{2} . \end{matrix}

Az előző megoldásban láttuk, hogy a

B C = a

oldal az adatokból megszerkeszthető, így megszerkeszthető a

B C C'

háromszög is a következő módon: Miután

a

-t megszerkesztettük, mint az előző megoldásban, mérjük fel egy egyenesre

C' C'' = 2 s

távolságot, ennek

C'

végpontjában az

\frac{α}{2}

szöget, a

C''

-től

a

távolságra levő

B

pont körül pedig rajzoljunk

a

sugárral kört (7. ábra).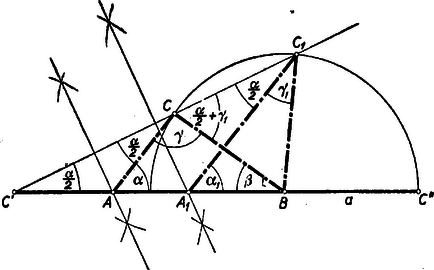

7. ábra

E körnek a szög másik szárával való valamelyik metszéspontja ‐ ha van ilyen ‐ legyen

C

. A

C C'

szakasz felező merőlegese metszi ki a

C' C''

szakaszból az

A

pontot.
Az

A B C

háromszög valóban megfelel a feltételeknek, mert szerkesztés szerint a

C A C'

háromszög egyenlő szárú, így

C A = C' A

, és a háromszög

A

-nál levő külső szöge

\begin{matrix} C A C'' ∢ = 2 \cdot C C' A ∢ = α . \end{matrix}

Ez az

A B C

háromszög belső szöge kell, hogy legyen. Ugyanis a szerkeszthetőséghez szükséges, hogy

a < s

legyen. Ez esetben

C'

a

sugarú

B

középpontú körön kívül van. Ha a kör és a

C' C

egyenes másik metszéspontját

C_{1}

-gyel jelöljük, akkor a

C C_{1}

szakasz felező merőlegese

B

-n megy át; mivel pedig

C C'

(és

C_{1} C'

) felezőpontja

C'

és a

C_{1} C

szakasz felezőpontja közé esik, így

A

-nak is

C'

és

B

közé kell esnie.

C A C'' ∢

tehát az

A B C

háromszögnek valóban belső szöge. A háromszög kerülete:

\begin{matrix} C A + A B + C B = C' A + A B + B C'' = 2 s . \end{matrix}

Így az I. megoldás (1) szerint a beírt kör érintési pontja

A

-tól

s - a

távolságra van. Ebből, mivel a beírt kör középpontja az

α

szög felezőjén van, a megszerkesztése szerint következik, hogy a beírt kör sugara olyan derékszögű háromszög befogója, melynek ezzel szemközti szöge

\frac{α}{2}

, a másik befogója pedig

s - a

. Mivel

a

-t egy ugyanilyen háromszög segítségével szerkesztettük, melynek emellett kérdéses befogója

ϱ

hosszúságú, így a megszerkesztett háromszög beírt körének sugara

ϱ

. A háromszög tehát megfelel a feladat feltételeinek.
Azt állítjuk, hogy ha

C

helyett

C_{1}

-ből kiindulva szerkesztünk egy

A_{1} B C_{1}

háromszöget, ez az előbbivel egybevágó lesz (a megfelelt csúcsok

A

C

és

B

). Valóban

A_{1}

C'

és

B

közé esik. Essék mondjuk a

C

C'

és

C_{1}

pontok közé, és jelöljük az

A B C

és

A_{1} B C_{1}

háromszögek szögeit

α

β

γ

, illetőleg

α_{1}

β_{1}

γ_{1}

-gyel. Szerkesztés szerint

α_{1} = α

a megadott szög.
A

B C C_{1}

egyenlő szárú háromszögből

\begin{matrix} B C C_{1} ∢ = B C_{1} C ∢ = γ_{1} + \frac{α}{2}, \end{matrix}

így a

C

-nél keletkező szögek összege

\begin{matrix} 180^{\circ} = C' C A ∢ + A C B ∢ + B C C_{1} ∢ = \frac{α}{2} + γ + γ_{1} + \frac{α}{2} = α + γ + γ_{1}, \end{matrix}

tehát

γ_{1} = β

. Az

A B C

és

A_{1} C_{1} B

háromszögek tehát hasonlók, mivel pedig

B C

és

C_{1} B

oldaluk egyenlő, tehát egybevágók is.

III. megoldás: Rajzoljuk meg a háromszög

B C

oldalához hozzáírt kört is. A betűzést a 8. ábra mutatja.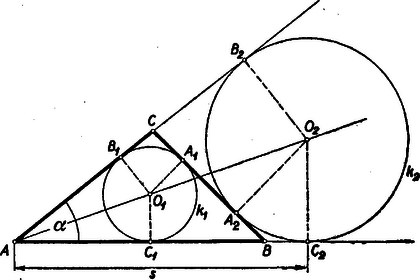

8. ábra

Ismeretes, hogy ekkor

\begin{matrix} A B_{2} = A C_{2} = s . \end{matrix}

(3)

(Valóban a körhöz egy pontból húzott érintők egyenlősége folytán

\begin{matrix} 2 A B_{2} = A B_{2} + A C_{2} = A C + C A_{2} + A B + B A_{2} = A C + A B + B C = 2 s .) \end{matrix}

Ez a következő szerkesztéshez vezet: Szerkesszünk

α

nagyságú szöget, csúcsa legyen

A

, és szerkesszük meg a két szárat érintő

ϱ

sugarú

k_{1}

kört. Mérjük rá a szög egyik szárára az

A C_{2} = s

távolságot, és szerkesszük meg azt a

k_{2}

kört, amelyik mindkét szárat érinti, egyiket

C_{2}

-ben. Húzzuk meg a két kör egyik közös belső érintőjét, messe ez a szög szárait

B

és

C

pontokban.

A B C

a keresett háromszög, mert

A

-nál levő szöge

α

, beírt körének sugara

ϱ

, és a (3) összefüggésből következik, hogy kerülete

2 s

.
A másik belső közös érintő meghúzása nyilvánvalóan a megszerkesztettel egybevágó háromszöghöz vezet.

3. feladat. A községből egy nő

10

óra

31

perckor elindult és egyenletesen haladva

13

óra

43

perckor érkezett B községbe. Ugyanezen a napon B-ből

9

óra

13

perckor indult el egy férfi ugyanazon az úton, és állandó sebességgel

11

óra

53

perckor ért A-ba. Útközben egyszerre értek egy hídhoz, amelyet a nő (miután egymás mellett elhaladtak)

1

perccel később hagyott el, mint a férfi. Mikor értek a hídhoz és hol vannak a híd végpontjai ?

I. megoldás: Az egész utat a nő 192 perc alatt tette meg, a férfi 160 perc alatt. Mivel mindketten egyenletesen haladnak, azért ugyanakkora út megtételéhez a nőnek és férfinak szükséges idők aránya mindig

\begin{matrix} \frac{192}{160} = \frac{6}{5} . \end{matrix}

Jelöljük a híd végigjárásához a férfinek szükséges időt ‐ percekben ‐

t

-vel, ekkora nő a feltétel szerint

t + 1

perc alatt jut át a hídon, és így

\begin{matrix} \frac{t + 1}{t} = 1 + \frac{1}{t} = \frac{6}{5}, t = 5 perc . \end{matrix}

A híd hosszát távolságegységnek választva, az egész út hossza (a férfi menetidejéből számítva)

\begin{matrix} 160 : 5 = 32 hídhossz . \end{matrix}

A híd eléréséig a nő és a férfi együtt 31 hídhossznyi utat tett meg. Ha a nő útja ebből

x

hídhossz volt, akkor, mivel a nő egy hídhosszat 6 perc alatt tesz meg, azért

6 x

idő alatt ért a hídhoz. A férfi 78 perccel korábban indult el, mint a nő, és (

31 - x

) 5 percig ment, míg a hídhoz ért. Mivel egyszerre értek a hídhoz, azért

\begin{matrix} 6 x = (31 - x) 5 - 78, \\ x = 7. \end{matrix}

Eszerint a nő (és ugyanakkor a férfi is) a nő elindulásától számított

6 x = 42

perc múlva ér a hídhoz, vagyis mindketten 11 óra 13 perckor érik el a hidat.
A híd

A

felőli hídfője 7 hídhossznyira van

A

-tól és így a másik hídfő 24 hídhossznyira

B

-től.

II. megoldás: A férfi 160 perc alatt teszi meg az egész utat és 78 perce gyalogol, mikor a nő elindul, tehát megtette már az út

\begin{matrix} \frac{78}{160} = \frac{39}{80} \end{matrix}

részét, együtt tehát még az út

\frac{41}{80}

részét teszik meg a találkozásig.
Mivel egyenletesen haladnak, mindketten, így sehességeik aránya

\begin{matrix} \frac{192}{160} = \frac{6}{5}, \end{matrix}

másszóval, ami utat a férfi 5 perc alatt tesz meg, azt a nő 6 perc alatt. Ebből mindjárt az is következik, hogy a hídon is 5, illetőleg 6 perc alatt haladnak át. A fenti arányt úgy is értelmezhetjük, hogy az ugyanazon idő alatt együttesen megtett útnak

\frac{5}{11}

-ét teszi meg a nő,

\frac{6}{11}

-ét a férfi. Így az egész útnak

A

-tól mért

\begin{matrix} \frac{5}{11} \cdot \frac{41}{80} = \frac{41}{176} \end{matrix}

részénél találkoznak, és ez a hídnak

A

-tól mért

\frac{5}{11}

részénél lesz. A híd hossza (a férfi menetidejéből számítva) az egész út

\begin{matrix} \frac{5}{160} = \frac{1}{32} \end{matrix}

része, így a híd

A

-hoz közelebb eső vége

A

-tól az út

\begin{matrix} \frac{41}{176} - \frac{5}{11} \cdot \frac{1}{32} = \frac{77}{352} = \frac{7}{32} \end{matrix}

részén, a túlsó vege pedig az út

A

-tól mért negyedrészére van.
A

B

-ből induló férfi a hídig terjedő utat, azaz az egész út

\frac{3}{4}

részét

\frac{3}{4} \cdot 160 = 120 perc = 2

óra alatt teszi meg, tehát mindketten 11 óra 13 perckor érnek a hídhoz.