Cím: Az 1956. évi Rákosi Mátyás matematikai verseny II. (döntő) fordulója
Füzet: 1956/szeptember, 1 - 10. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az április 17-én lefolyt II. (döntő) fordulóban az alábbi három feladat volt kitűzve:
1. A háromszög oldalait belülről érintő körhöz az a, b, c oldalakkal párhuzamosan húzott érintőknek a háromszög belsejében levő szakaszai legyenek rendre a1, b1, c1.
Bizonyítsuk be, hogy

a1a+b1b+c1c=1.

2. Bizonyítsuk be, hogyha
a=bz+cy,b=cx+az,c=ay+bx,
akkor
a21-x2=b21-y2=c21-z2.

3. Legyenek α, β, γ egy háromszög szögei. Bizonyítsuk be, hogy
ctg2α+ctg2β+ctg2γ≥1.

Mikor áll fenn egyenlőség ?
 

Öt órai munkaidő után 138 iskolában 364 dolgozatot adtak be.
A Bolyai János Matematikai Társulat által az Oktatásügyi Minisztériummal egyetértésben kiküldött központi bizottság (Horvay Katalin, Késedi Ferenc, Lőrincz Pál, Tolnai Jenő és Neukomm Gyula előadó) Surányi János, a Társulat főtitkárának elnökletével a május 12-iki ülésén a következő jelentést fogadta el:
A bizottság megállapítja, hogy a versenyzők teljesítménye ‐ annak ellenére, hogy a kitűzött feladatok a bizottság egyhangú véleménye szerint nehezebbek voltak a tavalyi feladatoknál ‐ jóval felülmúlja még a tavalyi jó eredményt is, amennyiben nem kevesebb, mint 44 versenyző oldotta meg lényegében mind a három feladatot, és két feladat megoldása az idén általában nem volt elég helyezés eléréséhez. Viszont az a tény, hogy a döntőben számos tanuló egy feladatot sem tudott megoldani, mutatja, hogy a tételek tényleg nem voltak könnyűek, bár meg kell állapítani, hogy a feladatok puszta megoldásához jó rutin munka is elegendő volt, viszont mind a három feladat bőven adott alkalmat minőségileg értékes megoldásokra, általánosításokra és érdekes speciális esetek felismerésére, ami már matematikai invenciót követel.
Meg kell azonban jegyezni, hogy az egy feladatra adott több megoldás között gyakran szerepeltek olyanok, amelyek az előző gondolatmenetet ismételték, többnyire még ügyetlenebbül, körülményesebben is. Az ilyen megoldások természetesen semmiképp sem emelik a dolgozat értékét.
A bizottság megállapítja, hogy a tanulók feladatmegoldása készségének e további fejlődése azt is tanúsítja, hogy az utóbbi négy év rendszeres matematikai tanuló versenyeinek, valamint a Középiskolai Matematikai Lapok állandó pontversenyeinek üdvös hatása most bontakozik ki először igazán.
14 tanuló teljesített többletmunkát a három feladat jó megoldásán felül. Ezek közül a bizottság alapos megfontolás után Stahl János, Makkai Mihály, Szatmáry Zoltán és Zsombok Zoltán dolgozatát emelte ki.
Stahl János az első feladatban az ábrát kiegészítve ötletesen használja fel két részábra hasonlóságát. A harmadik feladat megoldásában Jensen tételét alkalmazza, ennek révén egy lényeges általánosítást is ad. A második feladatra adott megoldása is elegáns. Mindegyik feladatra vannak további megoldásai is. A bizottság javasolja, hogy az 1. díjat Stahl János-nak ítéljék oda.
Makkai Mihály két feladatra adott megoldása igen ügyes, gondosan diszkutálja a felmerülő kivételes eseteket. Érdekes a legnehezebbnek bizonyult harmadik feladatra adott három különböző megoldása.
Szatmáry Zoltánnak mindhárom feladatra, de különösen az első és harmadik feladatra adott igen ügyes megoldást. Emellett szintén több megoldást keres az egyes feladatokra.
Zsombok Zoltán fő érdeme az első feladatra adott szép megoldása mellett egy térbeli általánosítás felismerése, bár ezt nem dolgozza ki. A második feladat taglalása nála a legteljesebb. A harmadik feladat megoldására nem találja meg a legegyszerűbb utat.
A bizottság e három dolgozatot egyenlő értékűnek ítélte, azért azt javasolja, hogy mind a három versenyző egyaránt 2. díjban részesüljön.
A többi 10 tanulót, akiknek teljesítménye csak kevéssel marad el a nyertesekétől, a bizottság I. dicséretre ajánlja. Lényegében három feladatot megoldott, vagy ezzel egyenértékű teljesítményt nyújtott 30 tanuló, míg két feladat megoldásánál többet, vagy két, minőségileg kiemelkedő, megoldást produkált 33 versenyző. A bizottság az előbbieket II. dicséretre, az utóbbiakat III. dicséretre ajánlja.
 

Az O. M. a fenti javaslat alapján a következő döntést hozta:
 


1. díj (oklevél + 1000 Ft):
Stahl János (Bp. VI., Kölcsey g. III. o. t.)
 


2. díj (oklevél + 500 Ft):
Makkai Mihály (Bp. V., Eötvös g. III. o. t.),
Szatmáry Zoltán (Bp. VIII., Piarista g. III. o. t.),
Zsombok Zoltán (Bp. IV., Könyves Kálmán g. IV. o. t.)
 


I. dicséretben és nagyobb könyvjutalomban részesült:
 

Beke Gyula (Hatvan, Bajza g. IV. o. t.)
Benkő Bálint (Sárospatak, Rákóczi g. IV. o. t.)
Csapody Miklós (Bp. VIII., Piarista g. III. o. t.)
Harza Tibor (Székesfehérvár, József Attila g. IV. o. t.)
Jedlovszky Pál (Bp. XIV., Petrik vegyip. t. IV. o. t.)
Literáthy Péter (Szeged, Irányi J. vegyip. t. III. o. t.)
Papp Kálmán (Bp. IX., Fáy g. III. o. t.)
Perneczky László (Kaposvár, Táncsics M. g. IV. o. t.)
Szabados József (Bp. III., Árpád g. IV. o. t.)
Szeidl Béla (Bp. V., Cukor u. gyak. g. IV. o. t.)
 


II. dicséretet és könyvjutalmat nyert:
 

Beliczky Tibor (Celldömölk, Gábor Áron g. III. o. t.), Berár István (Makó, József A. g. IV. o. t.), Budai László (Bp. V., Eötvös g. IV. o. t.), Czájlik István (Bp. II., Rákóczi g. IV. o. t), Daróczy Zoltán (Debrecen, Ref. g. IV. o. t.), Dobrovolszky András (Bp. I., Toldy F. g. III. o. t.), Fekete János (Bp. II., Rákóczi F. g. IV. o. t.), Frivaldszky Sándor (Bp. II. Rákóczi g. III. o. t.), Gáti Gyula (Debrecen, Vegyip. t. III. o. t.), Gelencsér László (Pannonhalma, Bencés g. III. o. t.), Grell Mihály (Bp. XVI., Corvin Mátyás g. III. o. t), Guba István (Mezőkövesd, I. László g. III. o. t.), Heinemann Zoltán (Pécs, Bányaip. t. III. o. t.), Horváth József (Orosháza, Táncsics g. IV. o. t.), Illés Csaba (Bp. VIII., Vörösmarty g. III. o. t.), Jakubovics János (Bp. V., Eötvös g. IV. o. t.), Jókúti Ferenc (Bp. VI., Kölcsey g. III. o. t.), Kelemen Péter (Bp. V., Eötvös g. IV. o. t.), Őri Viktor (Kaposvár, Táncsics g. IV. o. t.), Rázga Tamás (Bp. II., Rákóczi F. g. IV. o. t.), Réti Sándor (Bp. XVI., II. Rákóczi F. katonai középisk. IV. o. t.), Rockenbauer Antal (Bp. X., I. László g. III. o. t.), Ruppenthal Péter (Győr, Révai Miklós g. III. o. t.), Schipp Ferenc (Mohács, Kisfaludy K. g. III. o. t.), Simák Pál (Bp. I., Toldy F. g. III. o. t.), Solt György (Bp. VIII., Fazekas M. g. III. o.), Surán Gábor (Bp. VI., Kölcsey F. g. IV. o. t.), Szilárd András (Bp. II., Rákóczi g. III. o. t.), Udvari András (Bp. VIII., Piarista g. IV. o. t.), Veszely Gyula (Kőszeg, Jurisich M. g. III. o. t.)
 


III. dicséretben és könyvjutalomban részesült:
 

Argay Gyula (Balassagyarmat, Balassi B. g. III. o. t.), Böhm Róbert (Bp. IX., József A. gépip. t. IV. o. t.), Böröczky Károly (Bp. XVIII., Steinmetz g. III. o. t.), Csiszár Imre (Bp. I., Petőfi S. g. IV. o. t.), Daróczy Attila (Debrecen, Fazekas M. g. IV. o. t.), Demény Zoltán (Veszprém, Lovassy g. IV. o. t.), Deres János (Pécs, Bányaip. t. IV. o. t.), Farkas László (Ózd, József A. g. IV. o. t.), Finta Ida (Celldömölk, Gábor Áron g. IV. o. t.), Forgó Gábor (Bp. V., Eötvös g. IV. o. t.), Gárdos György (Bp. V., Eötvös g. IV. o. t.), Gergely Ervin (Bp. IV., Könyves K. gimn. III. o. t.), Geszti Tamás (Bp. VII., Madách I. g. IV. o. t.), Gulyás Gyöngyi (Diósgyőr, Kilián Gy. g. IV. o. t.), Hódossy Béla (Bp. IV., Könyves Kálmán g. IV. o. t.), Kim Hen Cse (Miskolc, Kohászati t. III. o. t.), Kocsis János (Eger, Dobó I. g. IV. o. t.), Koltai Henrik (Bp. IX., Fáy A. g. IV. o. t.), Komáromy Béla (Sárospatak, Rákóczi g. IV. o. t.), Kuti József (Veszprém, Lovassy g. IV. o. t.), Orlik Péter (Bp. V., Eötvös J. g. IV. o. t.), Óvári Ferenc (Székesfehérvár, József A. g. IV. o. t.), Polgár Előd (Bp. VIII., Széchenyi g. IV. o. t), Poór István (Kecskemét, Katona J. g. IV. o. t.), Soós Tibor (Bp. I., Petőfi g. III. o. t.), Szokoly Pál (Zalaegerszeg, Zrínyi M. g. III. o. t.), Teőke László (Bp. II., Rákóczi g. IV. o. t.), Tokai József (Esztergom, I. István g. III. o. t.), Tóth László (Miskolc, Vill. ener. ip. t. III. o. t.), Varga Sándor (Mezőkövesd, I. László g. IV. o. t.), Vásárhelyi Boldizsár (Bp. XI., József A. g. IV. o. t.), Zaránd Péter (Bp. VIII., Piarista g. III. o. t.), Zádor Miklós (Esztergom, I. István g. III. o. t.).
*

A verseny végeredményét megyék és iskolafajok szerint a 4. oldalon közölt táblázat mutatja.
Lapunk feladatmegoldóinak eredménye még további javulást mutat. A döntőben részt vett 364 tanuló közül 203 (55,8% ‐ tavaly 44,1%) volt lapunk munkatársa; a 77 helyezést elért versenyző közül azonban már 75 (97,4% ‐ tavaly 89,9%) tartozik lapunk feladatmegoldóinak táborába, s mindössze a III. dicséretet nyertek közt van két tanuló, aki lapunknak nem megoldója. (Részletes beszámoló ‐ sokféle szempontból ‐ a ,,Köznevelés'' szeptember 1-i számában jelent meg).
 

Kimutatás az 1956. évi Rákosi Mátyás matematikai verseny II. fordulójáról megyék és iskolafajok szerint
 


 Beadott dolg. számaEredményMegyék és Budapestgimn.ip.t.összesenDíjDicséretPontszám (nem hiv.) isk.tan.isk.tan.isk.tan.1.2.I.II.III.g.i. t.összesen 1. Baranya.....2625411‐‐‐21235 2. Bács-Kiskun.....3911410‐‐‐‐11‐1 3. Békés.....35‐‐35‐‐‐1‐2‐2 4. Borsod.....71722919‐‐1169211 5. Csongrád.....5824712‐‐11‐235 6. Fejér.....1723310‐‐1‐14‐4 7. Győr-Sopron.....61423817‐‐‐2‐4‐4 8. Hajdu-Bihar.....919221121‐‐‐21325 9. Heves.....37‐‐37‐‐1‐14‐410. Komárom.....3625511‐‐‐‐22‐211. Nógrád.....251136‐‐‐‐11‐112. Pest.....71411815‐‐‐‐‐‐‐‐13. Somogy.....411‐‐411‐‐11‐5‐514. Szabolcs-Szatmár.....241135‐‐‐‐‐‐‐‐15. Szolnok.....79‐‐79‐‐‐‐‐‐‐‐16. Tolna.....39‐‐39‐‐‐‐‐‐‐‐17. Vas.....25‐‐25‐‐‐215‐518. Veszprém.....51711618‐‐‐‐22‐219. Zala.....24‐‐24‐‐‐‐11‐119.Vidék.....76176192995205‐‐5121847105720. Budapest.....35*14881143159135181579483    Összesen.....111*32427401383641310303312614140*1 katonai középisk.

 

Alább közöljük a II. forduló feladatainak megoldását.
 

1. feladat.
 

I. megoldás: Az 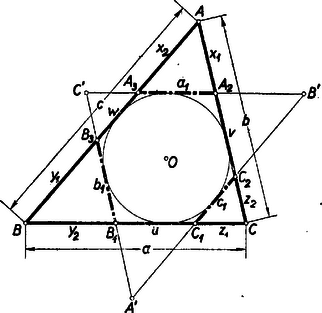a1, b1, c1 szakaszok által az adott ABC▵-ből lemetszett háromszögek nyilvánvalóan hasonlóak az ABC▵-höz. A jelölést az 1. ábra mutatja.
 
 
1. ábra
 

Ennek alapján
x1:b=a1:a
amiből
x1=a1ab.
Hasonlóképpen
x2=a1ac,y1=b1bc,y2=b1ba,z1=c1ca,z2=c1cb.

Az ABC▵ kerülete:
(u+v+w)+(x1+x2)+(y1+y2)+(z1+z2)=k.

Az érintő hatszög tétele szerint
u+v+w=a1+b1+c1,
és így
(a1+b1+c1)+a1a(b+c)+b1b(a+c)+c1c(a+b)==a1+b1+c1+a1a(k-a)+b1b(k-b)+c1c(k-c)==a1+b1+c1+a1ak+b1bk+c1ck-a1-b1-c1==k(a1a+b1b+c1c)=k.
Mindkét oldalt k-val osztva a bizonyítandó összefüggést kapjuk.
 

II. megoldás: Az előző megoldásban szereplő
y2=b1ba,z1=c1ca
összefüggéseket fogjuk felhasználni, emellett megmutatjuk, hogy
a1=u.
Ebből már következik az állítás, ha az
a=y2+u+z1=b1ba+a1+c1ca
összefüggést a-val osztjuk.
A bizonyítandó egyenlőség igazolására hosszabbítsuk meg az a1, b1, c1 egyeneseket, míg metszik egymást. A keletkező A'B'C'▵ oldalai párhuzamosak az ABC▵ megfelelő oldalaival, és beírt körük közös. Így a kiegészített ábra centrálszimmetrikus a beírt kör O középpontjára nézve. Tehát az u és a1 szakaszok is egymás tükörképei O-ra nézve, amivel állításunkat igazoltuk.
 

III. megoldás: Egészítsük ki az ábrát az 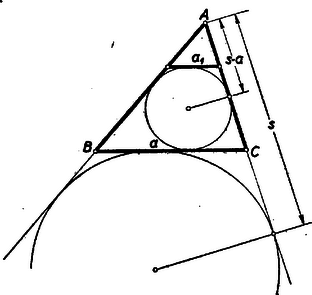AB oldalt és a másik két oldal meghosszabbítását érintő körrel (2. ábra).
 
 
2. ábra
 

A háromszög kerületét 2s-sel jelölve tudjuk, hogy a C csúcsból a két körhöz húzott érintő szakaszok hossza s-a és s. A beírt kör a C csúcsnál az a1 szakasszal levágott kis háromszögnek hozzáírt köre. Így e kis háromszögből és körből álló ábrarész hasonló az ABC háromszögből és hozzáírt köréből álló ábrarészhez. A kettőben egymásnak megfelelő szakaszok aránya tehát egyenlő. Így
a1a=s-as.
Hasonlóan
b1b=s-bs,c1c=s-cs.
Ezeket összeadva
a1a+b1b+c1c=3s-(a+b+c)s=3s-2ss=1.

Megjegyzések: 1. Néhány versenyző rámutatott, hogy tételünk a hozzáírt kör esetén is érvényes, ha a keletkező szakaszokat előjellel vesszük. Egy még messzebb menő általánosítást adott Udvari András. Megfogalmazásához először is tekintsünk két párhuzamos szakaszt egyező vagy ellenkezű előjelűnek aszerint, amint a két szakasz kezdőpontjától a végpont felé mutató irány megegyezik, vagy ellentétes.
Legyen egy ABC háromszögnek valamely, a síkjában fekvő, P pontjára vonatkozó tükörképe A'B'C'▵ és jelölje A'B' metszéspontját BC-vel és CA-val C1, illetőleg C2-vel, B'C' metszéspontját CA-val és AB-vel A2 ill. A3, végül C'A' metszéspontját BA ill. BC-vel B3, ill. B1-gyel, ekkor
A2A3CB+B3B1AC+C1C2BA=1.(1)

Az 1. ábrában a P szerepét O tölti be; ez esetben mind a három arányszám pozitív és az (1) helyességét az I., II., III. megoldásokban bebizonyítottuk.
Az általános esetet a 3. ábra mutatja.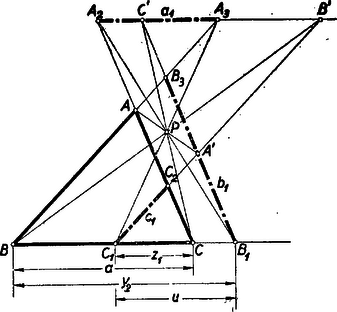
 
 
3. ábra
 

Mivel a pontra való tükrözés egy szakaszt ugyanakkora, de ellenkező előjelű szakaszba visz át:
A2A3CB=-A2A3BC=B1C1BC,B3B1AC=BB1BC,C1C2BA=C1CBC.


E három egyenlőség összeadásából adódik
A2A3CB+B3B1AC+C1C2BA=B1C1+BB1+C1CBC=BB1+B1C1+C1CBC=BCBC=1.



2. Egy térbeli általánosításra mutatott rá Zsombok Zoltán. Lásd a 772. sz. feladatot a 29. oldalon.
 

2. feladat.
 

I. megoldás: A megoldásnak egy természetesen kínálkozó (ha nem is legegyszerűbb) módja, hogy megoldjuk a feltételi egyenletrendszert és a nyert gyökök értékeit behelyettesítjük a bizonyítandó egyenlőségekbe.
 

A feltételi egyenleteket rendre a, b, c-vel szorozva
a2=abz+acy;(1)b2=bcx+abz;(2)c2=acy+bcx.(3)


(2)-ből abz értékét, (3)-ból acy értékét (1)-be helyettesítve
a2=b2+c2-2bcx.
Innen, ha b≠0, c≠0, akkor
x=b2+c2-a22bc,
tehát
1-x2=4b2c2-(b2+c2-a2)24b2c2==4b2c2-(a4+b4+c4+2b2c2-2a2b2-2a2c2)4b2c2==2(a2b2+a2b2c2+c2)-(a4+b4+c4)4b2c2


és így, ha x≠±1
a21-x2=4a2b2c22(a2b2+a2c2+b2c2)-(a4+b4+c4).

Ebben az alakban nyilvánvaló, hogy a, b, c és x, y, z egyidejű ciklikus felcserélésével a baloldal átmegy b21-y2, illetőleg c21-z2-be, míg a jobboldal önmagába megy át. Ezzel a feladat állítását bebizonyítottuk, arra az esetre, ha x≠±1, y≠±1 és z≠±1, a≠0, b≠0, c≠0.
Vizsgáljuk meg, mi a helyzet a kizárt esetekben.
1. Ha b=c=0, akkor az első egyenletből a=0. Ez az eset figyelmen kívül hagyható.
Ha pl. c=0, b≠0, akkor az első két egyenletből
z=ab=ba.

Innen z=±1 és a harmadik egyenletből
y=±abx=∓x
(vagy mindkét helyen a felső, vagy mindkét helyen az alsó előjel veendő) x tetszőleges lehet. Ez esetben tehát a következményben szereplő első két tört egyenlő, a harmadik értelmetlen.
2. Ha a≠0, b≠0, c≠0, de pl. x=±1, akkor kell, hogy az 1-x2-re kapott tört kifejezés számlálója 0 legyen. Mivel pedig az az a, b, c fölcserélésével nem változik, így egyszersmind 1-y2=1-z2=0 adódik, tehát a feladat következményében szereplő mindhárom tört értelmetlen.
 

II. megoldás: Kiküszöbölve z-t (1)-ből és (2)-ből, nyerjük, hogy
c(ay-bx)=a2-b2.
Ebbe c értékét 3-ból behelyettesítve
a2-b2=(ay+bx)(ay-bx)a2y2-b2x2.
Ez így is írható
a2(1-y2)=b2(1-x2),
ami egyenértékű a bizonyítandó első egyenlőséggel. Hasonlóan kapjuk a második egyenlőséget.
 

Megjegyzés: Az I. megoldásban felismerjük, hogy amennyiben a, b, c valamely háromszög oldalainak mértékszámai, akkor x éppen cosα.
A feltételi egyenletek ez esetben a következőkbe mennek át:
a=bcosγ+ccosβ,b=ccosα+acosγ,c=acosβ+bcosα.
Ez az oldalak előállítása a másik két oldal vetületeként. A bizonyítandó állításban pedig a sinus-tételt ismerhetjük fel.
Ez a trigonometriai összefüggés csak speciális esete a feladat állításának, mert a bizonyított tételünk akkor is érvényes, ha a, b, c tetszésszerinti számok.
E trigonometriai összefüggésre több versenyző rámutatott. Volt olyan is, aki ‐ mint láttuk, tévesen ‐ a trigonometriai összefüggést a feladat állításával egyenértékűnek vette, és ennek alapján vélte a kívánt bizonyítást szolgáltatni.
 

3. feladat.
 

A feladat megoldására a versenyzők többsége felhasználta a háromszög alkotórészei közti legkülönfélébb összefüggéseket és sokan hosszabb számítások után jutottak csak el a feladat igazolásához.
Ezen megoldási módok közül talán a legegyszerűbb a sinus és cosinus-tétel felhasználásával az oldalakat közvetlenül bevonni a számításunkba.
 
I. megoldás: Mivel
ctg2α=cos2αsin2α=1-sin2αsin2α=1sin2α-1,
azért
ctg2α+ctg2β+ctg2γ=1sin2α+1sin2β+1sin2γ-3.
Tehát a bizonyítandó egyenlőtlenség ekvivalens a következővel:
1sin2α+1sin2β+1sin2γ≥4.(1)

Szorozzuk meg (1)-et sin2γ-val
sin2γsin2α+sin2γsin2β+1≥4sin2γ=4(1-cos2γ)=4-4cos2γ.
A sinus-tétel, ill. cosinus-tétel alapján ez az egyenlőtlenség így is írható
c2a2+c2b2+1≥4-4(a2+b2-c22ab)2=4-(a2+b2-c2)2a2b2.
Mindkét oldalt a2b2-tel szorozva
b2c2+a2c2+a2b2≥4a2b2-(a4+b4+c4+2a2b2-2a2c2-2b2c2),
azaz rendezve
a4+b4+c4≥a2b2+a2c2+b2c2.(2)
Mindkét oldalt 2-vel szorozva, és 0-ra redukálva
2a4+2b4+2c4-2a2b2-2a2c2-2b2c2≥0,
ami így is írható
(a2-b2)2+(a2-c2)2+(b2-c2)2≥0.(3)

Ez azonban nyilvánvaló, mert valós számok négyzete nem lehet negatív. Egyenlőség jele csak a=b=c esetén érvényes.
Mivel csupa egyenértékű átalakítást végeztünk, azért (3)-ból kiindulva visszafelé következtetve (1)-hez jutunk. Ezzel a feladat állítását bebizonyítottuk.
 

Megjegyzés: Sok versenyző jutott el (2)-höz, de a befejező lépést nem találta meg.
 

II. megoldás: A bizonyítandó egyenlőtlenség baloldalát alakítsuk át a következőképpen
ctg2α+ctg2β+ctg2γ=12[(ctg2α+ctg2β)+(ctgβ+ctg2γ)++(ctg2γ+ctg2α)]==12[(ctgα-ctgβ)2+(ctgβ-ctgγ)2+(ctgγ-ctgα)2]++ctgαctgβ+ctgβctgγ+ctgγctgα.
Felhasználva, hogy α+β+γ=180∘, kapjuk, hogy
ctgγ=-ctg(α+β)=-ctgαctgβ-1ctgα+ctgβ
és ebből ctgα+ctgβ-val szorozva és átrendezve
ctgαctgβ+ctgβctgγ+ctgγ+ctgα=1.(4)
Ezt a fent nyert azonosságba helyettesítve
ctg2α+ctg2β+ctg2γ=1+12[(ctgα-ctgβ)2+(ctgβ-ctgγ)2+(ctgγ-ctgα)2]≥1.



Egyenlőség csak akkor állhat fenn, ha a három cotangens érték egyenlő, ami egy háromszög szögeire csak úgy következhetik be, ha α=β=γ=60∘.
A cotangensek négyzetösszege a minimális 1 értéket tehát egyedül a szabályos háromszögre veszi fel.
 

Megjegyzés: Felhasználhatjuk közvetlenül a számtani és mértani közép közötti ‐ a tananyagból ismert ‐ egyenlőtlenséget:
ctg2α+ctg2β+ctg2γ=ctg2α+ctg2β2+ctg2β+ctg2γ2++ctg2β+ctg2α2≥ctgαctgβ+ctgβctgγ+ctgγctgα.

Most már csak (4)-et kell bizonyítanunk. (A II. megoldás második átalakítása ennek a bizonyítását tartalmazza.)