Cím: Az 1956. évi Rákosi Mátyás Matematikai Tanulmányi Verseny I. fordulója
Füzet: 1956/május, 129 - 134. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez idén e versenyt március 6-án bonyolították le az egyes iskolákban a gimnáziumok és ipari technikumok III. és IV. osztályú tanulói részére változatlan feltételek mellett. Munkaidő 5 óra. Beadtak összesen 236 iskolában 3220 dolgozatot (tavaly 223/2823). Örvendetes a gimnáziumok számának megnövekedése (179-re 164-ről), viszont sajnálatos, hogy az ipari technikumok közül idén csak 57 indult a tavalyi 59-cel szemben.
A versenybizottság április 7-iki javaslata alapján 138 iskola 365 versenyzője ‐ a dolgozatot beadók 11,3 %-a ‐ került a II. (döntő) fordulóba (tavaly 136/341 ‐ 12,1 %). Részletes adatok iskolafajok és megyék szerint az itt közölt táblázatban találhatók.
A döntőbe került 365 tanuló közül csak 202 (55,3 % ‐ tavaly 43,4 %) lapunk feladatmegoldója, ami ismét mutatja, hogy még számos jóképességű tanuló van az országban, aki sikeresen vehetne részt a feladatmegoldói munkában.
A tavalyi versenyen helyezést nyert 26 III. osztályos tanuló 1 kivételével bekerült a döntőbe; a tavalyi Arany Dániel versenyen helyezést elért 32 II. osztályos tanuló közül 27-nek sikerült idén is a döntőbe jutnia.

 

Kimutatás az 1956. évi Rákosi Mátyás matematikai verseny
I. fordulójáról megyék és iskolafajok szerint
 

Beadott dolgozatokDöntőbe került
gimnáziumip.technikumösszesengimnáziumip.technikumösszeseniskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanulóiskolatanuló   1. Baranya615027815726254112. Bács-Kiskun8821298439114103. Békés111041171212135--354. Borsod811345012163717229195. Csongrád71183301014858247126. Fejér43433276617233107. Győr-Sopron1014254115183614238178. Hajdú-Bihar9116445131619192211219. Heves48011959937--3710.Komárom89131911110362551111. Nógrád22211733925113612. Pest8961891047141181513. Somogy664115779411--41114. Szabolcs8731497724113515. Szolnok131691111418079--7916. Tolna790--79039--3917. Vas8881198925--2518. Veszprém711823791555171161819. Zala22611734324--24 Vidék13617763637217221487617619299520520. Budapest43*8072126564107235*14981143160Összesen17925835763723632201113252740138365*1 katonai középiskola és 1 orosz-magyar iskola.

 

Az alábbiakban közöljük az I. forduló három feladatát a megoldásokkal együtt.
 

1. feladat. Legyenek a és a nála nagyobb b pozitív egész számok. Számítsuk ki az a és b közé eső, 7 nevezőjű, nem egyszerűsíthető törtek összegét.
 

I. megoldás: A 7 nevezőjű törtek sorozata (a-t és b-t is közéjük sorolva)
7a7,7a+17,7a+27,...,7b-17,7b7.(1)
Azonban e, sorozat tagjai közül
7a7,7a+77,...,7b7
egyszerűsíthető törtek, s a következő alakban írhatók
a,a+1,...,b.(2)

Az a és b közé eső, 7 nevezőjű, nem egyszerűsíthető törtek összegét az (1) és (2) számsorozatok összegének különbsége adja.
Az (1) sorozat olyan számtani sorozat, amelynek első tagja a, különbsége 17 utolsó tagja b. Ezekből az adatokból a tagok számát az n-edik tag ismert képlete felhasználásával nyerhetjük:
b=a+(n-1)17,ahonnann=7b-7a+1.


Így az (1) sorozat összege az összegképlet alapján:
S'=(7b-7a+1)(b+a)2.

A (2) sorozat az a-val kezdődő és b-vel végződő természetes számok sorozata, ezért összegére közvetlenül adódik
s=(b-a+1)(b+a)2.

Tehát a keresett tulajdonságú törtek összege
S=S'-s=(b+a)(7b-7a+1-b+a-1)2=(b+a)(6b-6a)2=3(b2-a2).

II. megoldás: a és a+1 közé eső, 7 nevezőjű, 6 törtszám összege
(a+17)+(a+27)+...+(a+67)=6a+217=6a+3.
Minden következő számközben a törtszámok egy-egy egységgel nőnek, tehát a 6 törtszám összege 6-tal nő.
Az a és b közé eső, 7 nevezőjű, nem egyszerűsíthető törtek összege ezért olyan számtani sorozat összege, amelynek első tagja 6a+3, különbsége 6, tagjainak száma b-a.
Tehát az összegképlet alapján nyerjük
S=b-a2[2(6a+3)+(b-a-1)6]=(b-a)(6a+3+3b-3a-3)==(b-a)(3a+3b)=3(b2-a2).



III. megoldás: A számításba jövő, nem egyszerűsíthető törtek ugyan nem alkotnak számtani sorozatot, de összegüket először a tagok növekedő, azután fogyó sorrendjében egymás alá írva:
S=(a+17)+(a+27)+...+(a+67)+(a+87)+...+(b-27)+(b-17),S=(b-17)+(b-27)+...+(b-67)+(b-87)+...+(a+27)+(a+17).

Az egymás alatt álló tagok összege mindig b+a, és két szomszédos egész szám között 6 ilyen tagpár van. Így nyerjük, hogy
2S=(b-a)⋅6⋅(b+a)=6(b2-a2),vagyisS=3(b2-a2).

2. feladat. Adva van egy egyenesszakasz és egy ezzel párhuzamos egyenes. Szerkesszük meg csak vonalzó segítségével a szakasz harmadrészét.
 

I. megoldás: Legyen AB az adott szakasz és e az adott egyenes. Vetítsük az AB szakaszt egy tetszőleges O pontból az e egyenesre, a DC szakaszba. Az ABCD pontok egy trapéz csúcspontjai. Ismeretes, hogy a trapéz nem-párhuzamos oldalainak metszéspontját az átlók metszéspontjával összekötő egyenes felezi a trapéz párhuzamos oldalait.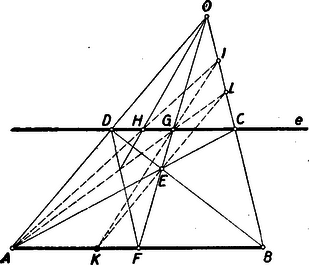
 
 
1. ábra
 

Az 1. ábrán az O pontot a trapéz AC és BD átlóinak E metszéspontjával összekötő egyenes az AB, illetve CD szakaszt az F, illetve G felezési pontokban metszi. Az ABCD trapézzal kapcsolatosan most végzett szerkesztésnek az AFGD trapézre való megismétlésével nyerjük a DG szakasz felezési pontját, a H pontot. Tehát a HG szakasz a HC szakasznak harmadrésze. Messe az AH egyenes az OB egyenest az I pontban, az I és G pontok összekötő egyenese az AB szakaszt a K pontban. Mivel az I pontból a HG és GC szakaszokat AK és KB szakaszokba vetítjük, ezért az AK szakasz az AB szakasznak harmadrésze. (Itt 10 egyenes vonalat használtunk fel a K pont szerkesztéséhez.)
 

Megjegyzés: Ha az O pont és e egyenes az AB szakasz által el vannak választva; akkor előfordulhat, hogy AH∥OB (vagyis az I pont a végtelenbe kerül), akkor a G pontnak az AH (ill. OB) egyenessel párhuzamos vetülete szolgáltatja az AB szakaszon a keresett K pontot.
 

II. megoldás: Ha már megszerkesztettük a CD szakasz G felezési pontját, akkor egyszerűbben is célt érünk. Messe az A és G pontokat összekötő egyenes az OB egyenest az L pontban, akkor megmutatjuk, hogy az LE egyenes és az AB szakasz K metszéspontjára AK az AB szakasz harmadrésze (1. és 2. ábra).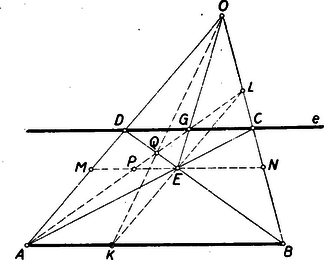
 
 
2. ábra
 

Ugyanis képzeljünk a trapéz átlóinak E metszéspontján át a párhuzamos oldalakkal párhuzamos egyenest, amely az OA és OB egyeneseket az M, illetve N pontban metszi (2. ábra). Ha az AG egyenes az utóbbi párhuzamost P pontban metszi, akkor MP=PE, mivel ezek a szakaszok az egymással egyenlő DG és GC szakaszoknak vetületei A-ból a párhuzamosra. Azonban ismeretes, hogy ME=EN, tehát PE a PN szakasz harmadrésze. Mivel végül L-ből a PE és EN szakaszokat az AK és KB szakaszokba vetítjük, ezért az AK szakasz valóban az AB szakasz harmadrésze. (Itt már 7 egyenessel célhoz jutottunk.)
 

Megjegyzés: Itt ugyanúgy előfordulhat mint az I. megoldásban, hogy AG∥ ∥OB. Ez esetben az E-nek AG-vel (ill. OB-vel) párhuzamos vetülete az AB szakaszon a keresett K pont.
 

III. megoldás: Ugyancsak 7 egyenest igényel a következő szerkesztés. A CD szakasz G felezőpontjának megszerkesztése után az AG és BD szakaszok Q metszéspontját kötjük össze az O ponttal (2. és 3. ábra). Az OQ egyenes metszi ki az AB szakaszból a keresett K harmadoló pontot.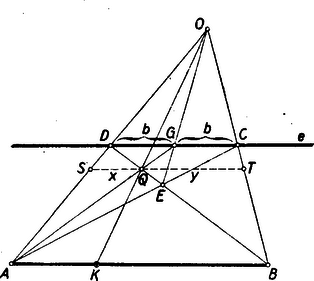
 
 
3. ábra
 

Bizonyítás: Legyen CG=GD=b. Messe a Q ponton átmenő AB-vel párhuzamos egyenes az OA és OB egyeneseket az S, ill. T pontban (3. ábra). Legyen SQ=x, QT=y. A szögek egyenlősége miatt AQSΔ∼AGDΔ, BQTΔ∼BDCΔ, ABQΔ∼GDQΔ.
Ennek alapján
x:b=AQ:AG=BQ:BD=y:2b,
amiből
y=2x,
és így az y és x szakaszokat O-ból az AB szakaszra vetítve a keletkező szakaszokra
KB=2AK.

3. feladat. Egy 2 méter átmérőjű köralakú biliárdasztal O középpontjától 12 méterre fekvő P pontban van egy biliárdgolyó. A golyót úgy kell ellökni, hogy kétszeri visszaverődés után ismét P-n haladjon át. Mekkora szöget zár be ez esetben az ellökés iránya a PO iránnyal ?
 

I. megoldás: Jelöljük a visszaverődési pontokat Q és R-rel (4. ábra).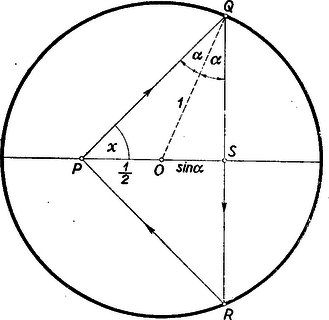
 
 
4. ábra
 

A PQRΔ egyenlőszárú és a szimmetria viszonyoknál fogva PO⊥QR. A beesési merőleges (a visszaverődési pontban a körérintőre merőleges egyenes) jelen esetben a QO körsugár. Legyen az OQP∢=OQR∢=α, a PO egyenes metszéspontja QR-re legyen S, a keresett OPQ∢-et jelöljük x-szel. Akkor OS=sinα, továbbá a feladat szerint OQ=1, és OP=12.
Felhasználva a szögfelező-tételt
OSOP=QSQP,
vagyis
2sinα=cos2α.
De cos2α=cos2α-sin2α=1-2sin2α, amely értéket a jobboldal helyére írva, és rendezve a
2sin2α+2sinα-1=0(1)
goniómetriai egyenlethez jutunk. Ennek egyik gyöke 1-nél nagyobb abszolút értékű, a használható gyök
sinα=3-12≈0,3660,és ígyα=21∘28'.
(A tompaszögű megoldás ismét nem jön tekintetbe.)
Tehát a keresett szög
x=90∘-2α=90∘-42∘56'=47∘4'.

II. megoldás: A szögfelező-tétel felhasználása nélkül is többféleképpen juthatunk az (1) egyenlethez. A legegyszerűbben úgy, hogy az OPQ háromszögre alkalmazzuk a sinus-tételt:
sinx:sinα=1:12,
amiből
sinx=2sinα.(2)

De sinx=sin(90-2α)=cos2α=1-sin2α, amely értékét (2)-be írva, nyerjük az (1) alatti egyenletet.
 

Megjegyzés: Azzal a triviális esettel, midőn a golyót a PO irányban lökjük el és az már egy (és tetszés szerinti számú) visszaverődés után halad át ismét a P ponton, nem kell foglalkozni, mert ezt az esetet a feladat szövege tulajdonképpen kizárja.