Kezdőlap


Cím:	Egyszerű nomogramok
Szerző(k):	Pálmay Lóránt
Füzet:	1956/november, 65 - 74. oldal	PDF \| MathML
Témakör(ök):	Szakmai cikkek

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Az $y = f (x)$ egyváltozós függvényt tudjuk ábrázolni a derékszögű koordinátarendszerben. A függvény görbéjéből az $x$ független változó és az $y$ függő változó összetartozó értékpárait le tudjuk olvasni; ily módon a függvény görbéje táblázatot helyettesít. Igaz, hogy a táblázat értékei pontosabbak, de a függvény görbéje áttekinthetőbb és gyorsabban kezelhető.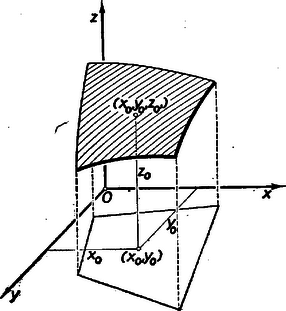
A $z = f (x, y)$ függvényt derékszögű térbeli koordinátarendszerben felülettel ábrázolhatjuk. Felveszünk egy $O$ pontból kiindult három, páronként egymásra merőleges tengelyt. A felvett $(x_{0}, y_{0})$ pontot megkeressük az $x$ , $y$ tengelyek síkjában. E pontban párhuzamost húzunk a $z$ tengellyel és az $(x_{0}, y_{0})$ pontból kiindulva felmérjük ezen egyenesre a függvénykapcsolatból adódó $z_{0}$ értéket. Ilyen módon általában felületet kapunk (1. ábra).

1. ábra

Elképzelhető, hogy egyes kétváltozós függvényekhez papír- vagy gipszmodell készíthető, azonban az ilyen modellek elkészítése és használata igen körülményes. Kettőnél többváltozós függvényeknél ilyen modelleket sem tudnánk készíteni.
Jól ismerjük azonban, hogy felületet lehet síkban ábrázolni. Erre szolgál a szintvonalas (rétegvonalas) térkép. Az azonos magasságban levű helyeket egy görbével kötjük össze.
2. Nézzük meg a

z = x y

függvény példáján, hogy egy, a térben felülettel ábrázolható kétváltozós függvényt hogyan ábrázolhatunk a síkban szintvonalakkal.
Tudjuk, hogy

x y = c

(konstans) görbéje a derékszögű koordinátarendszerben hiperbola, melynek aszimptotái a koordinátatengelyek. Ha

c

helyébe a

z

változó különböző értékeit téve ábrázoljuk a hiperbolákat (pozitív

x, y

és

z

értékek felvétele esetén a hiperbolák egyik ágát), akkor egy hiperbolasereget kapunk. Minden hiperbolához tartozik egy fix

z

érték, pl. az

x y = 1

görbéhez a

z = 1

x y = 2

-höz a

z = 2

stb. Ezt a

z

értéket a lerajzolt görbe mellé írjuk, és a görbe kótájának nevezzük (2. ábra).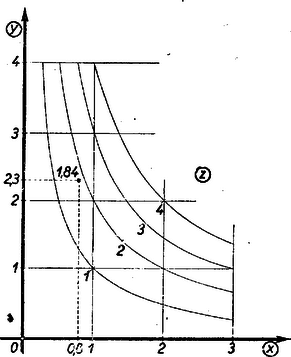

2. ábra

Az adott

(x_{0}, y_{0})

koordinátákkal rendelkező ponton áthaladó hiperbola

z_{0}

kótája adja az

x_{0} y_{0}

szorzat értékét. Ha a kérdéses ponton átmenő görbe nincs megrajzolva, akkor becsléssel kell megállapítani

z_{0}

értékét. Ezt az ábrát akkor is lehet használni, ha nem

x_{0}

és

y_{0}

, hanem például

x_{0}

és

z_{0}

adott. Az adott

x_{0}

pontból kiinduló

y

tengellyel párhuzamos egyenes, és az adott

z_{0}

kótájú görbe metszéspontjának

y

koordinátája adja a

\frac{z_{0}}{x_{0}} = y_{0}

hányados értékét.
Ezeknek a hiperboláknak a megrajzolása sok nehézséget okoz, különleges görbevonalzókra van szükség, és a becsléssel megállapított értékek akkor is igen pontatlanok, ezért ez az ábrázolás nem nagyon használható. A későbbiekben látni fogjuk, hogy az

z = x y

függvénykapcsolat praktikusabban is ábrázolható.
A többváltozós függvények síkbeli ábráját nomogram-nak nevezzük. A 2. ábra a

z = x y

függvénykapcsolathoz tartozó nomogram. A nomogramoknak a gyakorlatban nagy szerepük van. Ez az ábra használható pl. Ohm törvényénél

(V = I R)

, ha az egyik tengelyre az ellenállást, a másik tengelyre az áramerősséget mérjük fel. A görbék a feszültség különböző értékeivel lesznek kótázva.
Előbb a szorzáshoz (

x y = z

) készítettünk nomogramot. Lássunk ennél még egyszerűbb példát; ábrázoljuk nomogrammal a

z = x + y

függvénykapcsolatot. Ez

x

-ben és

y

-ban elsőfokú kifejezés, ezért, ha

z

állandó, egy egyenes egyenletét kapjuk:

y = - x + z

. Az egyenes meredeksége

- 1

, az

y

tengelyen levő metszete

z

. A meredekség

z

-től független, tehát, ha különböző

z

értékeket veszünk, egymással párhuzamos egyeneseket kapunk, amelyek az

x

tengely pozitív irányával

135^{\circ}

-os szöget zárnak be, ha a két tengelyen az egységek egyenlők (3. ábra).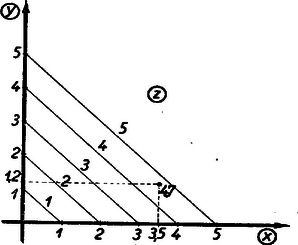

3. ábra

Nem szükséges, hogy a két tengelyen egyenlő egységeket vegyünk fel. Ti. ha egy elkészített nomogramot az egyik tengely irányában megnyújtunk, vagy összenyomunk, az egyenesek egyenesekbe mennek át és a párhuzamosság is öröklődik. Megváltozik azonban az egyeneseknek az

x

tengellyel bezárt szöge, a két tengelyen különbözők lesznek az egységek. Ilyenkor az egyeneseket legjobb két pontjuk segítségével megszerkeszteni. (A pontosság növelése érdekében gyakran az egyenes több pontját is megrajzolják, mielőtt meghúznák az egyenest. A most nyert párhuzamos egyenesek egy, az

x y

síkhoz hegyes szögben hajló sík rétegvonalai.)
Ennél a két példánál (

z = x y

és

z = x + y

) a koordinátarendszerben egy-egy kótázott görbesereg szerepelt. Az ilyen típusú nomogramokat görbesereges nomogramoknak nevezzük.
3. A nomogramok másik típusát jól megvilágítja a következő egyszerű példa: Ismerjük, hogy a trapéz középvonalának a hossza a két párhuzamos oldal számtani közepe. Húzzuk meg a trapéz két oldalegyenesét és a középvonal egyenesét, és skálázzuk ezeket egyenletes beosztással. (Egyenlő egységeket véve fel a három egyenesen.) Ekkor, ha egy vonalzót illesztünk a felső skála ,,

a

''-val és az alsó skála ,,

b

''-vel skálázott pontjához, akkor a vonalzó a középső skálának az

\frac{a + b}{2}

értékkel skálázott pontján fog áthaladni (4. ábra).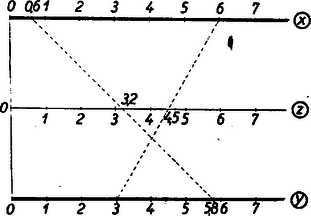

4. ábra

Az ábra mutatja. hogy pl.

3

és

6

számtani közepe

4, 5

.
Ezzel a

z = \frac{x + y}{2}

összefüggéshez egy új típusú nomogramot készítünk. Itt három skálázott vonalunk van. (Igen gyakran egyenesek szerepelnek, mint példánkban is.) Az egyik vonalon

x

, a másikon

y

, a harmadikon

z

értékeit tüntetjük fel. Az összetartozó

(x, y, z)

értékhármasok egy egyenesen fekszenek. Az ilyen típusú nomogramokat pontsoros nomogramoknak nevezzük.
Ha az elkészített nomogram középső skáláján, a szélső skálákon levő egység felével, mint egységgel készítünk egy egyenletes skálát, akkor az összeadáshoz (

z = x + y

) készítettünk pontsoros nomogramot (5. ábra).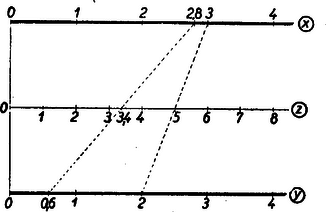

5. ábra

Itt sem szükséges, hogy

x

és

y

egyenesein ugyanakkorák legyenek az egységek. Képzeljük ui., hogy a fenti nomogramot üvegre karcoltuk és párhuzamosan vetítettük olyan síkra, amely az üveg síkjával nem párhuzamos, akkor egyenes egyenesbe megy át. Ha három pont egy egyenesen volt, akkor a három pont vetülete is egy egyenesen lesz. Az egységek különbözőek lesznek, de továbbra is egyenletes skálákat kapunk. A középen elhelyezkedő egyenes nem lesz pontosan középen. Gyakorlatban előfordulhat, hogy egyszerű összeadást kell ábrázolni nomogrammal, de

x

és

y

különböző határok között változik. Ilyenkor szükség van arra, hogy

x

és

y

egyenesein különböző egységeket vegyünk fel.
Természetesen, ha egy nomogram használható összeadásra, akkor használható kivonásra is. Ha

z

és

y

ismert, úgy az

z - y = x

-et az 5. ábrán az alsó skálán kapjuk meg. Ha állandóan kivonást akarunk végezni, akkor célszerű olyan nomogramot szerkeszteni, ahol az eredmény a középső skálán adódik. Így pontosabban olvashatjuk le az eredményt. Ilyen nomogramot kapunk, ha

x

egyenesén az irányítást ellenkezőjére változtatjuk, így

+ x

helyett

- x

-et kapunk (6. ábra).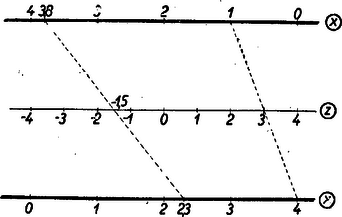

6. ábra

4. Az eddigiek alapján nagyon könnyen tudunk nomogramot készíteni Pythagoras tételéhez.

\begin{matrix} c^{2} = a^{2} + b^{2} . \end{matrix}

Láthatjuk, hogy itt is összeadásról van szó. Jelöljük

c^{2}

-et

z

-vel,

a^{2}

-et

x

-szel,

b^{2}

-et

y

-nal. Így

z = x + y

adódik. Ezt a kapcsolatot az ismert módon ábrázoljuk. Ebből az ábrából azonnal kapjuk Pythagoras tételéhez a nomogramot, ha

x

helyébe azt az ,,

a

'' számot írjuk, melynek négyzete

x

. Más szóval az egyenesen készítünk

x

-ben egy egyenletes skálát, s mivel

a = \sqrt[]{x}

, adott

x

értéke mellé az érték négyzetgyökét írjuk. (7. ábra felső egyenese.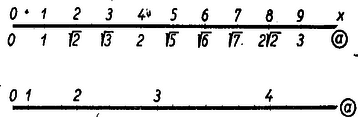

7. ábra

‐ Itt a feladat természetéből kifolyólag csak a pozitív négyzetgyök jön számításba.) Ilyen módon az egyenesszakaszunk

a

-val lesz skálázva, s kapjuk az ún. négyzetskálát. Az egyenes mellett csak ezt a skálát hagyjuk meg, ennek az elkészítésénél segédskálaként használt

x

egyenletes skáláját törüljük. Rendszerint a négyzetskálán is az egész értékeket írjuk ki. (7. ábra alsó egyenese, ahol kisebb egységet használtunk.)
Jelen példában mindhárom változóhoz a fent leírt módon négyzetskálát kell készíteni (8. ábra).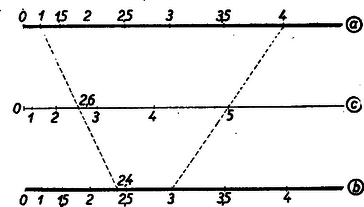

8. ábra

Pythagoras tételéhez igen egyszerűen készíthetünk egyenletes skálájú görbesereges nomogramot is. Vegyük fel ui. az (

a

b

) derékszögű koordinátarendszert. Ebben a rendszerben egy origó középpontú és

c

sugarú kör egyenlete

a^{2} + b^{2} = c^{2}

. Ha tehát

c

-nek különböző állandó értékeket adunk, akkor egy körsereget kapunk (9. ábra).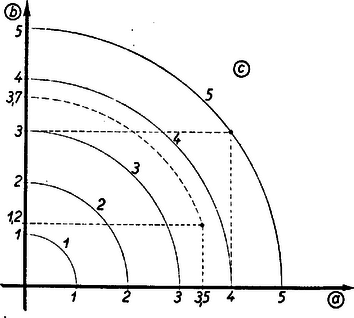

9. ábra

Itt is csak pozitív

x

y

és

z

értékekre szorítkoztunk.
5. A

z = x y

függvénykapcsolathoz már készítettünk görbesereges nomogramot. Megjegyeztük akkor, hogy ez a nomogram nem praktikus. Ez a kapcsolat egyenessereges nomogrammal is ábrázolható, mégpedig az egyeneseknek lesz egy közös pontjuk.
Készítsük el a nomogramot ui. úgy, hogy a koordinátatengelyekre az

x

és

z

változók kerüljenek, és

y

-nak adjunk különböző állandó értékeket. Így

z

-ben és

x

-ben elsőfokú kapcsolat adódik:

z = y x

alakból kiolvasható, hogy

y

rögzítése mellett az egyenes áthalad a koordinátarendszer kezdőpontján és iránytangense éppen az adott

y

(10. ábr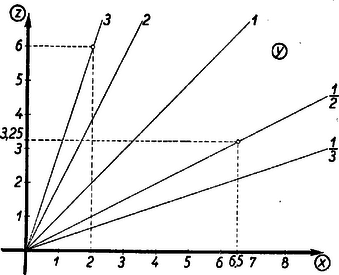a).

10. ábra

Ezt a nomogramot sugársoros nomogramnak nevezzük.
Természetesen itt sem szükséges, hogy a tengelyeken azonos egységeket szerepeltessünk.
A

z = x y

kapcsolatot visszavezethetjük az összeadásra is. Ui. vegyük mindkét oldal logaritmusát:

lg z = lg x + lg y

.
Hasonlóképpen, mint a Pythagoras-tétel ábrázolásánál tettük, új változókat vezetünk be

\begin{matrix} w = lg z; \end{matrix}

s így

w = u + v

adódik. Elkészítjük az összeadó nomogramot és utána átskálázunk.

u

-ban készítünk egy egyenletes skálát, s tetszőleges

u

értékhez azt az

x

értéket írjuk, amelynek logaritmusa

u

, más szóval

lg x

távolságra írjuk az

x

-et. Az így kapott skálát logaritmikus skálának nevezik; ez a logarléc alapskálája. Mivel a II. osztályos anyagban a logarléc tárgyalásánál szerepel a logaritmikus skála, így ezzel itt tovább nem foglalkozunk. Az olvasóra bízzuk, hogy ilyen módon elkészítse a nomogramot.
A szorzathoz készíthetünk más úton is pontsoros nomogramot. Ez a következő egyszerű észrevételen alapszik.
Vegyük az

y = x^{2}

parabolát és messük el egy

y

tengellyel nem párhuzamos egyenessel. Az egyenes egyenlete

\begin{matrix} y = m x + b . \end{matrix}

A metszéspontok

x_{1}

és

x_{2}

abszcisszái tehát az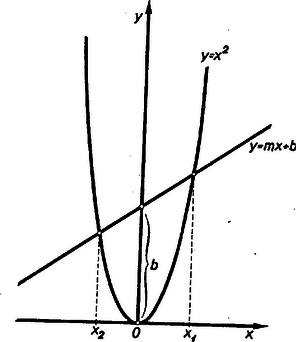

\begin{matrix} x^{2} - m x - b = 0 \end{matrix}

egyenlet gyökei (11. ábra), és így fennáll rájuk az

\begin{matrix} x_{1} x_{2} = - b \end{matrix}

összefüggés. Az előjelre a továbbiakban nem leszünk tekintettel, az mindig könnyen megállapítható külön. Így az

\begin{matrix} | x_{1} | | x_{2} | = | b | \end{matrix}

összefüggést fogjuk felhasználni.

11. ábra

Ennek alapján a következőképpen készíthetünk nomogramot: Az

x

és

y

tengelyen egyenlő egységeket veszünk fel, az

y

tengelyt egyenletesen skálázzuk, a parabola pontjaihoz írjuk a megfelelő pontok abszcisszáinak abszolút értékét. Ha elkészítjük ezt a nomogramot, akkor a következőképpen használhatjuk: megkeressük a parabolán a két összeszorzandó számot, az ezekhez tartozó pontokat egyenessel összekötjük, az

y

tengelyen metszi ki ez az egyenes a szorzat értékét (12. ábra).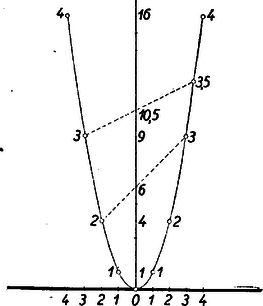

12. ábra

6. A

z = \frac{x}{y}

kapcsolatot nem kell külön tárgyalni, hiszen ez az előbbire visszavezethető. Itt talán legjobb a sugársoros nomogramot használni.
Sokszor jól használható a következő pontsoros osztó nomogram: Vegyünk fel egymástól eléggé távol két párhuzamos egyenest, s létesítsünk mindkét egyenesen egyenletes skálázást ellenkező irányítással. (Nem szükséges, hogy a két párhuzamos egyenesen egyenlő egységek legyenek.)

z = \frac{x}{y}

, a hányados skálája a nullapontokat összekötő egyenesen adódik.
A

z

skála

c

pontját ott kapjuk, ahol az

y

skála

1

-es pontját az

x

skála

c

pontjával összekötő egyenes a

z

skáláját metszi (13. ábra).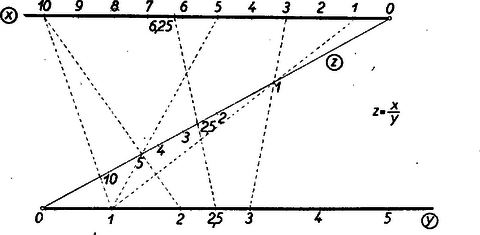

13. ábra

Igen egyszerűen látható, hogy ily módon valóban a

z = \frac{x}{y}

kapcsolatot ábrázoltuk.
A 14. ábrán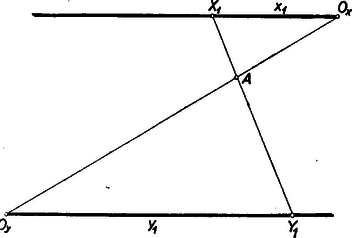

O_{x} A X_{1} ▵ \sim O_{y} A Y_{1} ▵

, ezért

\frac{x_{1}}{y_{1}} = \frac{O_{x} A}{O_{y} A}

14. ábra

\frac{x}{y}

arány egyértelműen meghatároz egy

A

pontot

O_{x} O_{y}

egyenesén. Így ez az egyenes skálázható

\frac{x}{y}

-nal.
Ennek a nomogramnak előnye a 10. ábrán szereplővel szemben, hogy csak három egyenest kell rajzolni. Ez a nomogram akkor is használható, ha logaritmust nem vehetünk.
Nagy hátránya azonban, hogy

z

skálája nagyobb értékeknél használhatatlanul sűrűvé válik.
Előfordulhat, hogy

x

és

y

olyan határok között változik, hogy nullapontjaik kiesnek az ábrából. Ilyenkor

z

skálájának egy pontját úgy szerkesztjük meg, hogy összekötjük az

x

skála

x_{1}

pontját az

y

skála

y_{1}

pontjával. Ezen az összekötő egyenesen lesz az

\frac{x_{1}}{y_{1}}

skálájú pont. Veszünk olyan

x_{2}

-t és

y_{2}

-t, melyekre

\frac{x_{2}}{y_{2}} = \frac{x_{1}}{y_{1}}

. Az

x_{2}

-t

y_{2}

-vel összekötő egyenes fogja kimetszeni az előbbi egyenesből

z

skálájának

\frac{x_{1}}{y_{1}}

-gyel skálázott pontját. A vázolt eljárással a

z

skála kellő sok pontját megszerkeszthetjük.
Ezt a nomogramot ferdeskálás, vagy ,,

Z

'' nomogramnak nevezzük.
7. Lényegében összeadásra és szorzásra vezethetők vissza a következő kapcsolatok:

α

)

\frac{1}{x} + \frac{1}{y} = \frac{1}{z}

. Új változókat bevezetve:

u = \frac{1}{x}

v = \frac{1}{y}

w = \frac{1}{z}

w = u + v

kapcsolatot kapjuk. Ezt ismertetett módon ábrázoljuk, és utána átskálázunk. Az ábrát nem készítjük el, mert az ilyen módon adódó nomogram nem igen használható nagyobb

x

y

vagy

z

értékek esetén. Ennek oka az, hogy reciprok skálákat alkalmazunk, s tudjuk, hogy minden

1

-nél nagyobb szám reciproka a

(0, 1)

számközbe esik; a skála nagyon sűrű lesz. Lehet azonban igen praktikus nomogramot készíteni ehhez a fontos, fizikában gyakran használt kapcsolathoz, amint az megtalálható a ,,Matematikai versenytételek'' I. részében (Tankönyvkiadó, 1955. 91. old.).

β

) Ábrázolandó

a x y + b x + c y + d = f (z)

függvénykapcsolat (

a

b

c

d

állandók,

a \neq 0

). E kapcsolatot átalakítjuk:

\begin{matrix} a (x + \frac{c}{a}) (y + \frac{b}{a}) - \frac{c b}{a} + d = f (z) . \end{matrix}

vagy

\begin{matrix} (x + \frac{c}{a}) (y + \frac{b}{a}) = \frac{1}{a} [f (z) + \frac{c b}{a} - d] = g (z) . \end{matrix}

(A jobb oldalon álló kifejezés csak

z

-től függ.) Új változókat vezetünk be:

u = x + \frac{c}{a}

;

v = y + \frac{b}{a}

;

w = g (z)

. Ekkor a kapcsolat

u v = w

alakú lesz. Ezt már tudjuk ábrázolni. Ábrázolás után a kapott nomogramot az előbbi példákhoz hasonlóan át kell skálázni.
Ilyen módon nagyon sok kapcsolat ábrázolható.

γ

) Ábrázoljuk az

x + y + z = x y z

kapcsolatot. Látni fogjuk, hogy egy ügyes ötlettel ez a kapcsolat is ábrázolható összeadó nomogrammal. Fejezzük ki a kapcsolatból

(- z)

-t

\begin{matrix} - z = \frac{x + y}{1 - x y} . \end{matrix}

Ezen kifejezés jobb oldala emlékeztet

tg (α + β)

kifejezésére. Ez adja azt a gondolatot, hogy vezessünk be új változókat a következőképpen:

x = tg α

;

γ = tg β

;

z = tg γ

,
ekkor

\begin{matrix} - tg γ = \frac{tg α + tg β}{1 - tg α tg β} = tg (α + β) . \end{matrix}

Tudjuk, hogy

\begin{matrix} tg (- γ) = - tg γ, \end{matrix}

és így

\begin{matrix} tg (- γ) = - tg (α + β), \end{matrix}

ahonnan:

- γ = α + β + k π

, ahol

k

tetszőleges egész. Ha

α = 0

β = 0

γ = 0

, akkor

x = 0

y = 0

z = 0

, s mivel a

(0, 0, 0)

számhármas kielégíti az eredeti kapcsolatot,

k

értékét nullának választjuk.

α + β + γ = 0

alakra jutottunk. Ezt tudjuk ábrázolni. Ábrázolás után átskálázásra van szükség. Ennek a példának inkább elvi jelentősége van, a skálák elkészítése még további bonyodalmakat okozna.

δ

) Az

u^{2} + p u + q = 0

valós együtthatós másodfokú egyenlethez pontsoros nomogram található a ,,Matematikai Versenytételek'' I. rész 92. oldalán. (Tankönyvkiadó, 1955.) Természetesen görbesereges nomogramot is lehet készíteni ezen kapcsolathoz.
8. Igen egyszerű egyenessereges nomogramokat lehet készíteni az

u + v + w = állandó

, ill.

u v w = állandó

‐ kapcsolatokhoz. Itt nem derékszögű koordinátarendszert alkalmazunk.
Vegyünk egy

c

oldalú egyenlő oldalú háromszöget. (A háromszög körüljárása legyen az óramutató járásával ellenkező irányú.) Vegyünk fel ezen háromszögön belül egy tetszőleges pontot, és ezen pontból az oldalakkal húzzunk párhuzamost. Ezen párhuzamosok az oldalakból

u

v

w

darabokat metszenek ki. (A háromszög irányított, így mindegyik oldalán meg tudjuk mondani, hogy melyik az első és melyik a második csúcs;

u

v

w

távolságokat mindig a megfelelő oldal első csúcsától mérjük.) A 15. ábrából közvetlenül leolvasható, hogy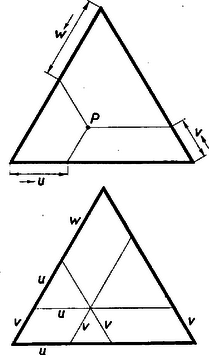

u + v + w = c

15. ábra

Ha a háromszög oldalaival párhuzamos egyenesseregeket rajzolunk, s ezt a

3

egyenessereget

u

-val,

v

-vel,

w

-vel kótázzuk, akkor az

u + v + w = c

kapcsolatot ábrázoltuk. Ha ezen egyenesek kótázásánál logaritmikus beosztást használunk, akkor ilyen nomogrammal ábrázolhatjuk az

u v w = k

kapcsolatot (

lg u + lg v + lg w = lg k

).
Így készülnek az ún. háromszög-nomogramok. (Háromszög-nomogramot készíthetünk nemcsak egyenlő oldalú háromszöggel.)
Az eddigiekben minden függvénykapcsolat

z = f (x, y)

alakú volt. A gyakorlatban többnyire nem szoktuk kitüntetni a független változót a függő változóval szemben. (Ohm törvényénél is lehetséges, hogy az ellenállást és az áramerősséget ismerjük és keressük a hozzájuk tartozó feszültséget, de ugyanúgy lehetséges, hogy a feszültség és az ellenállás, illetve a feszültség és az áramerősség ismert, és az áramerősséget, illetve az ellenállást keressük.) Éppen ezért a nomográfiában a függvényeket a szokástól eltérően osztályozzuk. Az

y = f (x)

függvényt szívesebben írjuk

F (x, y) = 0

alakban, és a függvényt kétváltozós kapcsolatnak mondjuk. (A két változó

x

és

y

; egyik sincs a másikkal szemben kitüntetve.) Hasonlóan

z = f (x, y)

helyett

F (x, y, z) = 0

-t írunk és háromváltozós kapcsolatról beszélünk.
Háromnál több változós kapcsolatokat is sok esetben nomogrammal tudunk ábrázolni, de erre itt nem térünk ki.

Röviden megismerkedtünk a nomogramokkal. Láttunk példákat görbesereges és pontsoros nomogramokra. A két típus összevetésénél a következőket mondhatjuk el:
A görbesereges nomogram előnye a pontsorossal szemben, hogy minden háromváltozós kapcsolat ábrázolható ezen a módon; használatához nincs szükség eszközre; kis darabja is használható (térkép). Idővel a levegő nedvessége miatt a nomogram papírja, s így maga a nomogram is deformálódik. Ez a deformáció a görbesereges nomogramnak nem árt, mert ha három görbe egy pontban metszette egymást, akkor deformáció után is egy pontban metszik egymást. (A három görbe közül többnyire kettő párhuzamos a koordinátatengelyekkel, s így ezeket nem is rajzoljuk be a nomogramba.) A görbesereges nomogram hátránya a pontsoros nomogrammal szemben, hogy áttekinthetetlenebb. Többnyire több időt vesz igénybe a megrajzolása. Pontatlanabbul használható. Ha sok görbe van berajzolva, könnyen hibázhatunk a görbe kótájának leolvasásánál.
A pontsoros nomogram előnyei: áttekinthető, könnyű megrajzolni és használni a nomogramot. A leolvasás általában pontosabban hajtható végre. A nomográfia magasabb fejezeteiben nagy szerepet játszanak a pontsoros nomogramok. Hátrányai viszont, hogy nem minden háromváltozós kapcsolat ábrázolható így, és sokszor nehéz eldönteni egy kapcsolatról, hogy lehet-e pontsoros nomogrammal ábrázolni. A nomogram használatánál asztalra, vonalzóra van szükség. A papír deformációja árt a nomogramnak, mert, ha

3

pont egy egyenesen volt, a deformáció után már általában nem lesz egy egyenesen.
Az elmondottakból látszik, hogy terepen inkább görbesereges, hivatalokban inkább pontsoros nomogramot használnak.
A nomográfiával a múlt század második felében kezdtek foglalkozni. D'Ocagne és Soreau sokat dolgoztak a nomográfia fejlesztéséért. A nomográfiának nagy gyakorlati jelentősége van; a technikában, iparban ma már szinte nélkülözhetetlenek a nomogramok. Előnyük elsősorban abban van, hogy igen egyszerűen és gyorsan használhatók bonyolultabb összefüggések esetén is. Nagy gyakorlati felhasználhatóságuknak köszönhető, hogy az utolsó 10‐15 évben hatalmasat fejlődött a nomográfia. Az elmúlt években igen jelentős sikereket értek el a nomográfia fejlesztésében a szovjet matematikusok.