|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Alább közöljük a haladók (II. osztályosok) versenyén kitűzött feladatok megoldásait:
I. forduló
1. feladat: Igazoljuk, hogy egész szám.
I. megoldás: A gyökjel alatti kifejezések így alakíthatók át: , és hasonlóan . Mivel , így a gyökmennyiségek pozitív értékét véve ami valóban egész szám.
Célhoz érhetünk azonban a felhasznált átalakítás lehetőségének észrevétele nélkül is.
II. megoldás: A vizsgálandó érték pozitív. Számítsuk ki a négyzetét: | |
Így a két gyök különbsége 2, ami valóban egész szám.
Jegyzet: Hasonlóan belátható, hogy ha és , akkor
Megjegyzés: A legnagyobb hiba, amit a versenyzők egy része elkövetett az volt, hogy a négyzetgyökök értékét számította ki közelítőleg tizedestörtekben, és így vélte a kívánt igazolást szolgáltatni. ‐ Igen sokan nem vették észre, hogy a vizsgálandó különbség pozitív, és értékének a >><<-t is megadták.
2. feladat: Adva van egy kör és a körön kívül fekvő P pont. Szerkesszünk P-től a körhöz érintőket, és jelöljük az érintési pontokat A-val és B-vel. A körnek B-vel átellenes pontja legyen D. Bocsássunk az A pontból merőleges egyenest a BD átmérőre, ennek talppontja legyen C. Bizonyítsuk be, hagy a PD egyenes felezi az AC szakaszt.
I. megoldás: Legyen és metszéspontja , továbbá messe a egyenes a kör -ben húzott érintőjét -ben (1. ábra). 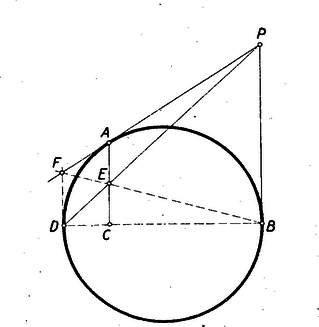 1. ábra
Bebizonyítjuk, hogy a trapéz átlóinak metszéspontja. Egyrészt mint egy pontból húzott érintők. Az átlók metszéspontja az átlókat a párhuzamos oldalak arányában osztja, ugyanúgy, mint az szakaszt, tehát az -t az átlók metszéspontjával összekötő egyenes párhuzamos a párhuzamos oldalakkal s így azonos az egyenessel.
Ismert tétel szerint az átlók metszéspontja felezi a rajta át a párhuzamos oldalakkal párhuzamosan húzott szakaszt, s így a feladat állítását igazoltuk.
II. megoldás: Messe meghosszabbítása -t -ban (2. ábra). 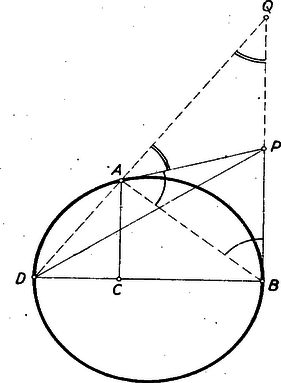 2. ábra
Mivel az háromszög egyenlő szárú, így az derékszögű háromszögben a és szögek egyenlő szögeket pótolnak -ra vagyis az háromszög is egyenlő szárú. Így , tehát a háromszög súlyvonala, tehát felezi a -val párhuzamos szakaszt is, és ez volt a bizonyítandó.
III. megoldás: Az egyenes párhuzamos a pontot a kör középpontjával összekötő egyenessel (3. ábra). 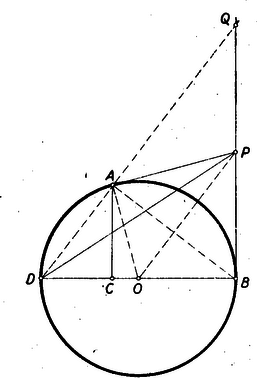 3. ábra
Ugyanis az egyenes merőleges -re. Thales tétele szerint, -ra pedig azért, mert utóbbi szögfelezője, az előbbi pedig alapja az egyenlőszárú háromszögnek.
Mivel felezi a szakaszt, ezért is felezi a egyenesnek -től az egyenessel való metszéspontjáig terjedő szakaszát. tehát súlyvonala a háromszögnek s így felezi a -val párhuzamos szakaszt is. Ezzel igazoltuk a feladat állítását.
Jegyzet: és párhuzamossága sok más úton is belátható, például így: az kerületi szög fele az középponti szögnek (3. ábra). Mivel a két szög -n átmenő szárai egy egyenesbe esnek, így párhuzamos a középponti szög felezőjével, ez pedig a egyenes, mert a négyszög deltoid.
Megjegyzés: Itt a leggyakoribb hiba az volt (mint az a bizonyítási feladatnál általában lenni szokott), hogy a bizonyítandó tétellel egyenértékű állítást használtak fel a versenyzők bizonyítás nélkül. Pl. az 1. ábrában feltételezték, hogy és szakaszok egy egyenesen vannak stb.
3. feladat: Az ABC egyenlőoldalú háromszög oldala . A háromszög A és B csúcspontjából egyszerre indul egy-egy pont, az AC oldalon , ill. a BC oldalon egyenletes sebességgel és halad C-ig. Mikor lesz a két mozgó pont egymástól mért távolsága egyenlő a háromszög magasságával?
Megoldás: Legyen másodperc múlva az -ból induló pont helyzete , a -ből indulóé . Jelöljük vetületét az egyenesen -rel (4. ábra). 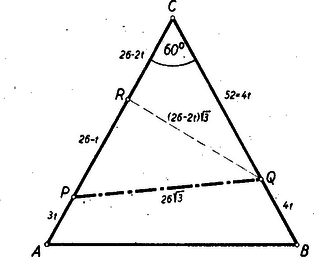 4. ábra
Számítsuk ki a derékszögű háromszög befogóit. s így a -os derékszögű háromszögből | |
tehát A feladat követelménye szerint -nak méternek kell lennie, ebből a
egyenlet adódik, vagy 13-mal osztva Innen A második gyök nem jön számításba, mert 26 másodperc múlva már mindkét pont a megfelelő oldal meghosszabbításán mozogna, így másodperc múlva következik be a kívánt helyzet.
Megjegyzés: A versenyzők egy része nem jött rá arra, hogy .
II. forduló
1. feladat: Melyik az az időpont és óra között, amelyhez található és óra közötti időpont úgy, hogy a két időpontban az óramutatók állása ‐ felcserélt mutatókkal ‐ megegyezik.
I. megoldás: A mutatóknak az óralapon megtett útját célszerű a teljes körüljárás -ad részével (a nagymutató percnyi útjával) vagy -ed részével (a kismutató egy órai útjával) mérni.
A és óra közti mutatóállásnál legyen a kismutatónak a órától kezdve megtett útja, a körüljárás -ad részében mérve . Ekkor a kismutató a -es számtól egységnyire van, a nagymutató pedig -nyire.
Ha óra után egységnyit mozdult el a kismutató a felcserélt mutatókkal ugyanezen álláshoz, akkor a második helyzetben a kismutató -nyira a nagy pedig -nyira van a -estől. Feltétel szerint
kell hogy legyen. Innen | |
Tehát a keresett időpont | |
A megfelelő időpont és óra között | |
II. megoldás: Az ismeretlenek meghatározására abból is nyerhetünk egyenleteket, hogy bármely időpontban olyan arányban osztja a kismutató a két szomszédos egész órát jelölő szám közti ívet, mint amilyen a -es számtól az egyik és másik irányban a nagymutatóig terjedő ívek aránya.
Válasszuk egységnek a teljes kör -ed részét, a kérdéses mutatóállásnál legyen az egyik mutató a -es szám után beosztással, a másik a -os után beosztással. Ekkor a fenti megjegyzést a és óra közti időre vonatkoztatva és óra közötti mutatóállást tekintve pedig Ezekből Ha még tekintetbe vesszük, hogy itt a mértékszámok ötödei az előző megoldásban szereplő és értékeknek, akkor láthatjuk, hogy lényegében az ott szereplő egyenletrendszert kaptuk vissza.
III. megoldás: Egy ismeretlennel is megoldhatjuk a feladatot. Az első megoldás jelöléseit használva a kis és nagymutató helyét és óra közt a és elfordulások adják most. Ha most a kismutató van és közt a helyen, akkor a nagymutató helyzetét a elfordulás jelzi, tehát Itt tulajdonképpen nem tettünk egyebet, mint hogy okoskodás útján küszöböltük ki az első megoldás egyenletrendszerében szereplő ismeretlent.
Jegyzet: Sokan választották a mutatók helyzetének meghatározására a következő utat (az elfordulásokat ismét a teljes kör -ed részével mérve): A és óra közti mutató állásánál a nagymutató és közt van. Ez azt jelenti, hogy a kicsi a -es számtól legalább és legfeljebb távolságra lehet. Ekkor és óra közt a nagymutató van a -estől számítva és -del jelzett határok közt, tehát a kicsi a után legalább -del, de legfeljebb -del kell hogy legyen. Ekkor azonban a nagymutató is ezen határok közt van és közt, vagyis a -től mérve legalább és legfeljebb -nyire. Így a kismutatóról azt is tudjuk, hogy a -estől legalább -nyire és legfeljebb -nyire van. Hasonlóan szűkíthetők egyre jobban a mutatók helyzetére adható határok. Pl. -ad beosztás (vagyis perc ugyanennyied része) kevesebb mint másodperc, tehát már a kapott értékek is jó közelítést adnak. Alkalmas ez a fokozatos közelítési eljárás a pontos érték meghatározására is, azonban ennek a keresztülvitele lényeges új fogalmak tisztázásán keresztül történhetne csak, ami nem állna arányban a feladat nehézségével.
Megjegyzés: Feltűnően sok versenyző idegenkedett a pontos eredményt szolgáltató közönséges törtektől és inkább közelítő értéket szolgáltató tizedestörtekkel számolt pontatlanul.
2. feladat: Szerkesszünk háromszöget, ha adna van az egyik oldala, a, és a másik két oldalhoz írt (kívülről érintő) körök és sugara.
I. megoldás: A feladatot megoldhatjuk számítás segítségével. Jelöljük az érintőkörök középpontját és -vel, érintési pontjukat a egyenesen és -vel (5. ábra). 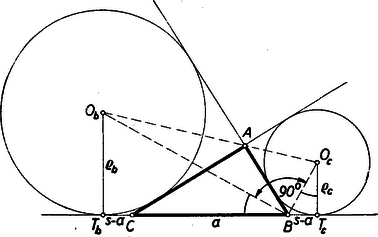 5. ábra
Ismeretes, hogy , ahol a háromszög kerületének felét jelenti. -t összekötve a körközéppontokkal tudjuk, hogy és a háromszög -nél levő belső és külső szögfelezői, és így egymásra merőlegesek.
Ebből következik, hogy mint merőlegesszárú szögek egyenlők, következőleg és háromszögek hasonlók. A befogók arányát felírva | |
Innen -et kiszámítva (a pozitív gyököt véve)
Ez a távolság megszerkeszthető; a második tag pl. a következő módon: mérjük fel egy egyenesre közös pontból ellenkező irányban a távolságot (6. ábra). 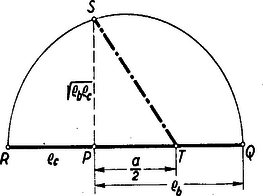 6. ábra
Az egyenesre -ben emelt merőleges messe a , mint átmérő fölé emelt félkört -ben akkor ‐ mint ismeretes ‐ . -ből felmérve a egyenesre (bármelyik irányban) a távolságot
, alapján a egyenesen megszerkeszthetjük a és , pontokat. A többi már triviális.
II. megoldás: Az előző megoldás jelöléseit használva, ott azt láttuk be, hogy az szakasz a pontból ‐ és természetesen ugyanúgy a pontból is ‐ derékszögben látszik. Ezt az előbbinél sokkal egyszerűbben is felhasználhatjuk a háromszög megszerkesztésére. A nyert összefüggés szerint az , mint átmérő fölé emelt félkör átmegy -n és -n (7. ábra). 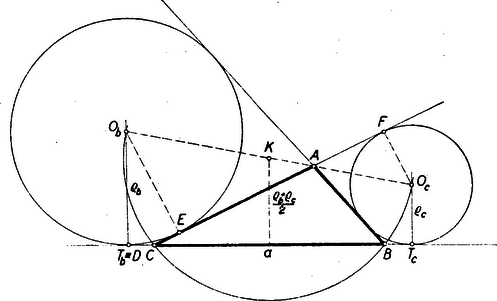 7. ábra
A kör középpontjából a egyenesre bocsátott merőleges egyrészt felezi a szakaszt, mint a kör húrját, másrészt hossza, mint az trapéz középvonala hosszúságú.
Ennek alapján a szerkesztés a következőképpen történhetik: Egy hosszúságú szakasz felezőpontjában hosszúságú merőlegest emelünk (8. ábra). 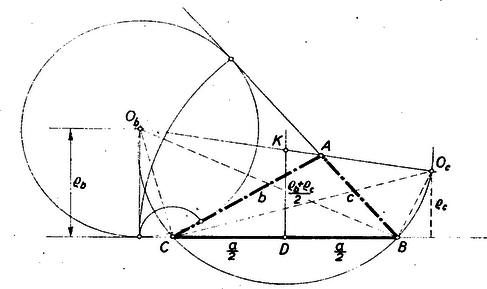 8. ábra
Megrajzoljuk a középpontú -n és -n átmenő kört és ennek a egyenestől a pont felé eső félkörét elmetsszük a egyenestől távolságban. Az pont körüli, egyenest érintő kör -ből és -ből húzott érintője lesz a háromszög másik két oldala.
Be kell látnunk, hogy a háromszög megfelel a feltételeknek, tehát hogy oldalához hozzáírt kör , sugarú. Azt mutatjuk meg, hogy e hozzáírt kör középpontja a középponttal rajzolt kör pontjával átelenes , pont és ez a egyenestől távolságra van. Az előbbi következik abból, hogy , a háromszög pontban levő belső szögének és a csúcsú külszögnek a szögfelezőin van. Ennek igazolására tekintsük az középpontú sugarú kört. Ez szerkesztés szerint hozzáírt köre a háromszögnek, tehát felezi a csúcsnál levő külső szöget, pedig a -nél levő belső szöget. Így a és egyenesek, amelyek az előbbiekre merőlegesek, valóban felezik a -nél levő belső szöget, ill. a -nél levő külső szöget. Másrészt -ből és -ből merőlegest bocsátva a egyenesre trapézt kapunk, amelynek -ből induló párhuzamos oldala hosszúságú, -ból induló középvonala pedig hosszúságú. Így az -ből induló oldal hossza valóban .
III. megoldás: Készítsünk vázlatot (7. ábra). A oldalhoz hozzáírt sugarú kör érintse a egyenest -ben, -t -ben, az oldalhoz hozzáírt sugarú kör -n levő érintési pontja legyen ; a háromszög kerületének felét jelöljük -sel.
Ekkor tehát
Ennek alapján a következő szerkesztés nyerhető: hosszúságú szakaszhoz rajzoljunk ellenkező oldalról -ben érintő sugarú és -ben érintő sugarú kört (9. ábra). 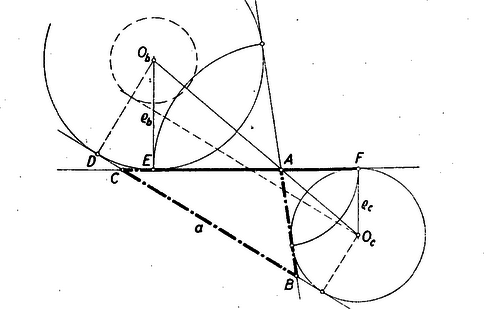 9. ábra
Szerkesszük meg a második belső közös érintőt és egy külső közös érintőt. Az érintők zárják közre a kívánt háromszöget. Jelöléseket az ábra szerint választva azt kell igazolnunk, hogy , ez pedig a fenti számoláshoz hasonlóan következik: | |
Megjegyzés: A helyes megoldók többsége csak bonyolult számításokkal oldotta meg a feladatot.
3. feladat:.A sík egyenese, melyek között párhuzamosak nincsenek, legfeljebb hány részre osztja fel a síkot? Ezek között hány síkrész véges területű?
Megoldás: Azt fogjuk megállapítani, hogy egy újabb egyenes meghúzása mennyivel növelheti a síkrészek számát. Az első egyenes a síkot két részre osztja. Egy második egyenes, ha metszi az elsőt, mindkét síkrészből egy-egy újabb síkrészt választ le, s így két egyenes részre osztja a síkot. Egy harmadik egyenes, ha metszi az első kettőt különböző pontokban, akkor három síkrészt oszt újra ketté, s így -mal szaporítja a síkrészek számát. Egy negyedik egyenes annyi síkrészt oszt tovább, ahány részre ezt az egyenest az előzőkkel való metszéspontjai osztják. A negyedik egyenes tehát legfeljebb -gyel szaporíthatja a síkrészek számát, annyival akkor, ha mindegyik egyenest metszi, de nem megy át semelyik kettő metszéspontján.
Általában ha egyenes van a síkban és meghúzunk egy -ediket ezt az előzőkkel való metszéspontok részekre osztják (véges szakaszokra és a két szélső metszésponttól végtelenbe nyúló két félegyenesre). Az egyenes minden egyes része egy-egy síkrészt kettéoszt. Az -edik egyenesnek az előzőkkel maximálisan metszéspontja lehet (ha nem megy át az előző egyenesek metszéspontjain), és ezek -részre osztják az egyenest. Ha tehát egyenest egymásután húzunk meg, az első két részre osztja a síkot, a továbbiak sorra -szal szaporítják a síkrészek számát, ha nincs köztük párhuzamos és semelyik egyenes nem megy át egy ponton. Így egyenes
részre osztja a síkot.
Egymás után húzva az egyeneseket, végtelenbe nyúló síkrészek csak végtelenbe nyúló síkrészekből keletkezhetnek. Végtelenbe nyúló síkrész elvágása esetén csak akkor lesz mindkét rész végtelenbe nyúló, ha a részekre osztó egyenesnek végtelenbe nyúló része osztja ketté, mert a feltétel szerint nem lehetnek az egyenesek között párhuzamosak. Így minden egyenes -vel szaporítja a végtelenbe nyúló síkrészek számát. Mivel ez első egyenes is végtelenbe nyúló részre osztja a síkot, így kétszer annyi a végtelenbe nyúló síkrészek száma, mint az egyeneseké. Speciálisan a egyenes szolgáltatta síkrészek közül lesz végtelenbe nyúló.
Jegyzet: 1. Ugyanúgy akárhány egyeneshez meghatározhatjuk, hogy mekkora a legtöbb síkrész száma, amelyre ennyi egyenessel fel lehet a síkot osztani. A síkrészek megszámlálásához azt kellett tudni, hogy a keletkező metszéspontok az egyenest hány részre osztják. Hasonló gondolatmenettel tovább is lehet menni annak meghatározására, hogy adott számú síkkal a teret hány részre lehet osztani.
2. A végtelenbe nyúló síkrészeket összeszámlálhatjuk a következőképpen is. Kerítsük körül az egyenesek összes metszéspontját pl. egy elég nagy körrel. Ez a kör a végtelenbe nyúló síkrészeken halad keresztül, mindegyikbe egy íve esik; mivel párhuzamos egyenesek nincsenek, nem eshet két ív ugyanabba a síkrészbe, így annyi síkrész nyúlik a végtelenbe, ahány részre az egyenesek a kört osztják. egyenes esetén ezek a kört pontban metszik és ugyanennyi ívre is osztják, tehát egyenes esetén: , speciálisan egyenes esetén: a végtelenbe nyúló síkrészek száma.
Megjegyzés: Számos versenyző a feladat szövegében szereplő >>egyenes<< fogalmát összetévesztette a >>szakasz<< fogalmával. Természetesen megoldást nem találhatott.
Matematika gimnáziumok II. osztálya számára. Tankönyvkiadó 1953. 30. old. |
|
 PDF | MathML
PDF | MathML