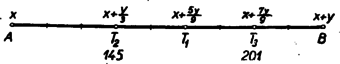Cím: Az 1955. évi Arany Dániel matematikai tanulóverseny (2. közlemény)
Füzet: 1955/október, 33 - 40. oldal  PDF  |  MathML 
Témakör(ök): Arany Dániel

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Alábbiakban közöljük a kezdők (I. osztály) versenyén kitűzött feladatok megoldásait.

 

Az I. forduló feladatai:
 

1. feladat. Egy motorcsónak sebessége a km/óra, egy gőzhajóé b km/óra. Mindkét jármű az AB utat teszi meg, de a motorcsónak csak akkor indul, mikor a hajó már d km-t meglett. Az utóbbi mégis n órával később érkezik B-be, mint az előbbi. Mekkora az AB távolság?
 

I. megoldás. A motorcsónak az AB=x km távolságot
xa
óra alatt teszi meg. A motorcsónak indulásától kezdve a hajó x-d km-t tesz meg B-ig; ezt b km/óra sebességgel haladva
x-db
óra alatt teszi meg. Ez n órával több, mint a motorcsónak menetideje, tehát
x-db=xa+n.
Innen
(a-b)x=ad+abn,
tehát ha a≠b, akkor
AB=x=a(bn+d)a-bkm.  

Az a, b, d, n adatok pozitív számok és a megoldásnak is csak akkor van értelme a feladat szempontjából, ha pozitív.
A feladatnak tehát csak akkor van megoldása ha a>b (ez nyilvánvaló is), és akkor mindig van egy megoldása.
 

II. megoldás. A feladatnak nyilvánvalóan csak akkor lehet megoldása, ha a>b. Ekkor a motorcsónak óránként a-b km-t hoz be a gőzhajó előnyéből. A motorcsónak az AB úton utoléri a hajót, sőt még akkora előnyt is szerez, amennyit a hajó n óra alatt tud megtenni, vagyis bn km előnyt. A d km hátrány behozásához és a bn km előny megszerzéséhez
d+bna-bóra
időre van szüksége a motorcsónaknak. Ennyi idő alatt teszi tehát meg az AB¯ utat, s így a megtett út hossza
AB=abn+da-bkm

 

2. feladat. Az ABC▵ A csúcsából kiinduló belső szögfelező messe a BC = a oldalt egy D pontban, a külső szögfelező pedig ugyanennek az oldatnak meghosszabbítását egy E pontban. Milyen összefüggés van az ABC háromszög szögei között, ha AD = AE?
 

Megoldás: A betűzést az 1. ábra mutatja.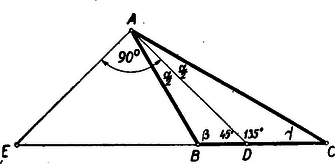
 
 
1. ábra
 

Mivel a feltétel szerint az ADE▵ egyenlő szárú, a belső és külső szögfelező pedig egymással merőleges azért
ADB∢=45∘,
és így
ADC∢=135∘.

Az ADC, ill ADB háromszögekre a külső és belső szögek közötti összefüggést felhasználva
γ+α2=45∘,(1)γ+β2=135∘.(2)



(1) és (2)-ből következik, hogy
β=135∘-α2=135∘-(45∘-γ)=90+γ,
és így
α=180∘-(β+γ)=180∘-(90∘+2γ)=90∘-2γ.

Tehát a háromszög szögeire fennáll,
γ<45∘,β=90∘+γ,α=90∘-2γ.(3)

Fordítva, ha a (3) alatti összefüggések teljesülnek, akkor α, β γ mind pozitívok, és összegük 180∘, és így szerkeszthető (pl. kiindulva egy tetszőleges 45∘-nál kisebb γ szögből) olyan háromszög, amelynek ezek a szögei. Ebben a háromszögben teljesülnek az (1) a (2) alatti egyenlőségek, vagyis az ABC▵ α szögének AD felezője a DB iránnyal
α2+γ=45∘
nagyságú szöget zár be. Ha AE az α szög külső szögének a felezője akkor EAD∢=90∘, és így AED∢-45∘, vagyis ADE▵ egyenlő szárú azaz
AD=AE.

Tehát a (3) alatti összefüggések teljesen jellemzik a feladat követelményeinek megfelelő háromszögeket.
 

3. feladat. Két szám negyedik hatványúnak különbsége mikor osztható 5-tel?
 

I. megoldás: Öttel való oszthatóság eldöntésére elegendő egy szám utolsó jegyét nézni. Hatvány utolsó jegye viszont csak az alap utolsó jegyétől függ, így egyszerű számítással adódik, hogy a negyedik hatvány utolsó jegye, ha az alap utolsó jegye
0,1,2,3,4,5,6,7,8,9
sorra
0,1,6,1,6,5,6,1,6,1
lesz. Két negyedik hatvány különbsége tehát 0-ra vagy 5-re végződik, s így osztható 5-tel, kivéve azt az esetet, ha az egyik hatványozott szám osztható öttel, a másik pedig nem.
 

II. megoldás. Annak eldöntésére, hogy egy különbség osztható-e 5-tel, elég ezt a maradékot nézni, amely adódik, ha a kisebbítendőt, ill. kivonandót 5-tel osztjuk.
Szükségünk lesz ennek megvizsgálásához arra az észrevételre, hogy egy szám négyzete 5-tel osztva ugyanazt a maradékot adja, mint az 5-tel való osztásból származó maradékának a négyzete. Valóban, ha
a=5k+r,
akkor
a2=25k2+10kr+r2=5(5k2+2kr)+r2,
s így a2-nek 5-tel osztva ugyanannyi a maradéka, mint r2-nek.
Legyen most már a és b két egész szám.
Ekkor
a4-b4=(a-b)(a+b)(a2+b2).

Ha a két szám ugyanannyi maradékot ad 5-tel osztva, akkor az első tényező osztható 5-tel. (Beleértjük azt az esétet is, ha mind a két szám osztható 5-tel, azaz ha mindkét maradék 0.) Ha a két szám maradéka 1 és 4, vagy 2 és 3, akkora második tényező osztható 5-tel.
Maradnak még azok az esetek, amelyekben a két szám maradéka 1 és 2, 1 és 3, 4 és 2, 4 és 3, mert ha az egyik szám 0 maradékot ad, a másik pedig 0-tól különböző maradékot 5-tel osztva, akkor a negyedik hatványok különbsége nyitván nem osztható 5-tel. Az 1 és 4 maradékot adó számok négyzete 1-et, a 2 és 3 maradékot adó számok négyzete pedig, 5-tel osztva, 4-et, ad maradékul, s így a hátralevő négy esetben a fenti szorzat harmadik tényezője osztható 5-tel.
Azt nyertük tehát, hogy két szám negyedik hatványának különbsége csak akkor nem osztható 5-tel, ha az egyik szám osztható 5-tel a másik nem,
Jegyzet: Válasszuk b-t 1-nek, ekkor eredményünk azt adja, hogy
a4-1
mindig osztható 5-tel, ha a nem osztható 5-tel. Ez speciális esete Fermat következő nevezetes tételének:*1
Ha p prímszám, a pedig bármilyen p-vel nem osztható szám, akkor
ap-1-1
osztható p-vel.
 

A II. forduló feladatai:
 

1. feladat. Egy háromszög α és β szögének szögfelezője messe a háromszög köré irható kört a D és E pontban. Mekkora szögeket zár be a DE szakasz a háromszög γ szögének szögfelezőjével?
 

I. megoldás. Legyen a C-ből induló szögfelező és DE metszéspontja F, a szögfelezők metszéspontja O. (2. ábra. ‐ Felhasználjuk tehát azt a tételt, amely szerint a belső szögfelezők egy pontban metszik egymást.)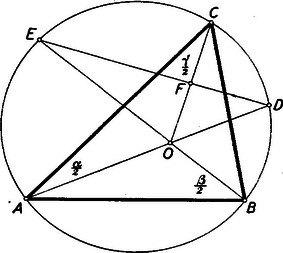
 
 
2. ábra
 

Ekkor, mint az AOC▵ külső szöge
COD∢≡FOD∢=α2+γ2.

A kerületi szögek tétele szerint
ADE∢≡ODF∢=β2.

Így a DFO háromszögből
DFO∢=180∘-(ODF∢+FOD∢)=180∘-α+β+γ2=90∘.



DE tehát merőleges a C-ből induló szögfelezőre.
 

II. megoldás: A D ill. E pont felezi a körülírt körnek a BC, ill. AC oldalak fölötti ívét. Így az egyenlő íveken nyugvó kerületi szögek egyenlő volta miatt a CDOE négyszögben a DE átló felezi a végpontjainál levő szögeket (3. ábra), tehát szimmetria-tengelye a négyszögnek. (A négyszög deltoid.)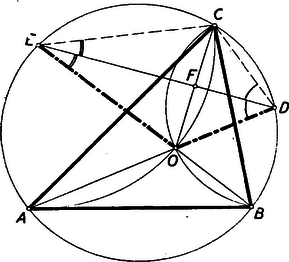
 
 
3. ábra
 

Mivel C és O egymás tükörképei DE-re nézve, azért
DE⊥CO,
de CO a C-ből induló szögfelező, mert O-n kell átmennie a harmadik szögfelezőnek is.
 

III. megoldás: A CDOE négyszög deltoid voltát a következőképpen is bizonyíthatjuk:
Ha a B és C pontokat rögzítjük és A végigfut a BEC^ íven, akkor O annak a körnek BC ívén fut végig, amelynek középpontja D (3. ábra ‐ lásd a tavaly A. D. verseny I. forduló 1. feladatát a K. M. L. 1954 októberi számában). Hasonlóképpen A és C rögzítése és a B pont mozgása esetén O mértani helye az E középpontú AC körív. Tehát
DC=DOésEC=EO,
ami bizonyítandó volt.
*

 

A további megoldások nem használják fel a szögfelezők metszéspontjára vonatkozó tételt.
 

IV. megoldás. Jelölje G a C-ből húzott szögfelező metszéspontját a körrel (4. ábra).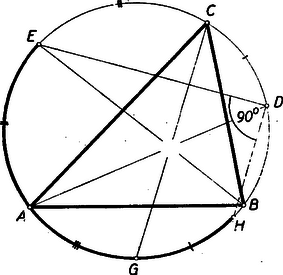
 
 
4. ábra
 

D, E és G felezik a háromszög oldalai feletti köríveket. Húzzunk D-ből párhuzamost CG-vel. Legyen ennek második metszéspontja a körrel H. Ekkor
CH⌢=CD⌢,
így az EAGH^ körív a három oldal fölötti körívnek felerészeiből tevődik össze, vagyis félkör.
Ebből következik, hogy
EDH∢=90∘,
és így a DH||CG összefüggés folytán
DE⊥CG.

Megjegyzés: Tulajdonképpen azt az általános tételt bizonyítottuk az itt szereplő speciális esetre, hogy két húr szöge akkora, mint a szög és csúcsszögével szemközti ívek összege fölötti kerület szögek a körben. Az itt használt bizonyítás tetszés szerinti húrokra átvihető.
A feladat néhány további megoldása lényegében e tétel más segédvonalak alapján történő bizonyításaiban állt. (Ezeket itt nem közöljük.)
 

V. megoldás: Messe a DE egyenes az AC és BC oldalt K-ban és L-ben. Több versenyző azt mutatta ki, hogy a CKL háromszög egyenlő szárú. Ebből következik, hogy DE merőleges a C-ből induló szögfelezőre, mert egyenlőszárú háromszögben az alap és a csúcsnál levő szög szögfelezője merőlegesek egymásra.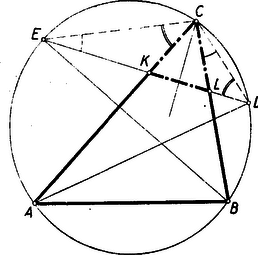
 
 
5. ábra
 

Az egyenlőszárúság például így látható be egyszerűen: Mivel E felezi az AC körívet, D a BC körívet (5. ábra), azért
CED∢=BCD∢ésACE∢=CDE∢,
mint egyenlő köríveken nyugvó kerületi szögek. Ebből következik, hogy a CKE▵ és DLC▵ harmadik szögei is egyenlők, amelyek egyben a CKL▵ háromszög K-nál és L-nél levő külső szögei.
Így a CKL háromszög egyenlő szárú.
 

VI. megoldás: Legyen C0 az AB fölötti C-t tartalmazó körív felezőpontja. Az ABC0 egyenlőszárú háromszőg C0-ból induló szögfelezője az ábrának szimmetriatengelye s így az ABC0 másik két szögfelezőjének, D0 és E0 metszéspontjait összekötő egyenes merőleges rá (6. ábra).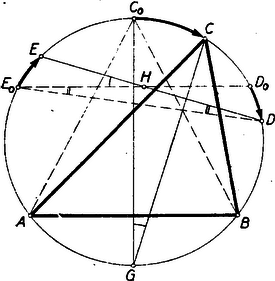
 
 
6. ábra
 

Ha most C0 elmozdul a kör mentén C-be, akkor D0 és E0 ugyanolyan irányban feleakkora körívvel mozdulnak el. Legyen D0 E0 és DE metszéspontja H. A mondottak szerint
D0E0D∢=EDE0∢=12C0GC∢.

Ennek folytán, mint az E0DH háromszög külső szöge
E0HE∢=HE0D∢+HDE0∢=C0GC∢,


vagyis a DE egyenes ugyanakkora szöggel fordult el, mint a C csúcsból induló szögfelező, merőlegességük tehát megmaradt.
 

2. feladat. Egy műút két pontjából, A és B-ből egyszerre indul egy-egy gépkocsi egymással szembe. Sebességük állandó, aránya 5:4 (az A-ból induló a gyorsabbik). A két gépkocsi A és B között ide-oda cirkál. Másodszor a 145-ös km-kőnél, harmadszor a 201-es km-kőnél találkoznak. Hányas km-kőnél fekszik A és B?
 

I. megoldás: Nevezzük a két gépkocsit röviden a-nak és b-nek. Feküdjön A az x km-kőnél és B az (x+y) km-kőnél. Jelöljük az első, második és harmadik találkozási pontot rendre T1, T2, T3-mal.
Az első találkozásig a két gépkocsi együttvéve y km utat tesz meg. A feladat szerint AT1:T1B=5:4, amiből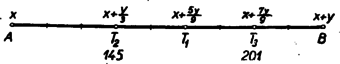
 
 
7. ábra
 

AT1=5y9(7.ábra).

A második találkozásig együttesen 3y km utat tesznek meg, tehát a megtesz 3⋅5y9=15y9=y+6y9=y+2y3 km-t, és így T1 az x+y-2y3=x+y3 km-kőnél fekszik.
A harmadik találkozásig a két gépkocsi együttvéve 5y utat tesz meg, amiből a-ra esik 5⋅5y9=25y9=2y+7y9, tehát T2-nél az x+7y9 km-kő van. A feladat szerint
x+y3=145,(1)
x+7y9=201,(2)
amiből
y=126ésx=103.

Tehát A a 103-as, B a 103 + 126 = 229-es km-kőnél fekszik.
Célszerű az x ismeretlent egyelőre teljesen figyelmen kívül hagyni, amikor is y-ra olyan egyszerű egyenletet ‐ tudniillik (2) és (1) különbségét ‐ nyerünk, amely már következtetéssel pótolható, amint azt az alábbi megoldás mutatja.
 

II. megoldás: Az a és b jelöléseket megtartva az első találkozásig a az AB útszakasz 59-ét, b a 49-ét teszi meg. Minden további Két találkozás közt a két gépkocsi együtt az AB szakasz kétszeresét teszi meg, tehát a az útszakasz 109-ét, b a 89-ét. Így a második találkozás az útszakasz A-tól számított 13-án történik, a harmadik pedig az A-tól számított 79-én. A két találkozás helyének 56 km-es távolsága tehát az AB szakasz 49 része. A harmadik találkozástól 29 útszakasznyira tehát a 229-es kilométerkőnél van B, A pedig az útszakasz 13=39-ével azaz 42 km-rel a második találkozás helye előtt, tehát a 103-as kilométerkőnél.
 

3. feladat. Igazoljuk, hogy ha n természetes szám, akkor 2n-1, 2n+1, 22n+1 számok egyike osztható 5-tel.
 

I. megoldás: Figyeijük meg, hogy páros számot 6-tal szorozva az utolsó számjegy változatlan marad, két egész szám szorzatának utolsó jegyét pedig a tényezők utolsó számjegyei szorzatának az utolsó jegye adja. Így mivel 24 utolsó jegye 6, tehát 25,29, általában tetszés szerinti pozitív egész k-ra 24k+1 ugyanarra a jegyre végződik mint az első hatvány, vagyis 2-re, hasonlóan 24p+2 utolsó jegye 4, 24k+3-é 8, végül 24k-é 6.
Így 2n+1 akkor és csakis akkor végződik 5-re, ha az n kitevő 4k+2 alakú, 2n-1 akkor és csakis akkor, ha 4k alakú a kitevő 2n aszerint 4k+2 alakú, vagy 4k alakú, amint n páratlan, vagy páros. Így 22n+1 az első esetben 5-re, a másodikban 7-re végződik. Azt kaptuk tehát, hogy ha a természetes szám, akkor a
2n-1,2n+1,és22n+1
számok közül az egyik és csakis az egyik osztható mindig 5-tel.
 

II. megoldás. 2n-1 és 2n+1 szomszédos páratlan számok, tehát utolsó jegyeik 1 és 3 vagy 3 és 5, vagy 5 és 7, vagy 7 és 9 vagy 9 és 1 lehet. A második és harmadik esetben a feladat állításának helyessége nyilvánvaló. Az ötödik nem fordulhat elő, mert ekkor
(2n-1)+(2n+1)=2⋅2n=2n+1
10-zel, tehát 5-tel is osztható volna, ami lehetetlen. A fennmaradó első és negyedik esetben az utolsó jegyek szorzata egyformán 3-ra végződik, tehát (2n-1)(2n+1)=22n-1 utolsó jegye 3, s így (22n+1)-é 5, tehát ez osztható 5-tel.
 

III. megoldás: Elég megmutatni, hogy a feladatban szereplő három szám szorzata osztható 5-tel, mert 5 prímszám, és prímszámoknak megvan az a tulajdonságuk, hagy egész számok egy szorzatának csak úgy lehetnek az osztói, ha osztói valamelyik tényezönek.2
A négy szám szorzata:
(2n-1)(2n+1)(22n+1)=(22n-1)(22n+1)=24n-1=(24)n-1
mindig osztható 24-1=15-tel, tehát 5-tel is.
Az eredmény mutatja, hogy a három szám valamelyike mindig osztható 3-mal is.
Jegyzet. Ez a megoldás világosan mutatja a feladat kapcsolatát az I. forduló 3. feladatával kapcsolatban említett Fermat-féle tétellel.
 

IV. megoldás: Mivel
22n+1=22n-4+5=(2n-2)(2n+2)+5,
így ez a szám akkor és csak akkor osztható 5-tel, ha jobboldalon szereplő szorzat osztható 5-tel.
De
2n-2,2n-1,2n,2n+1,2n+2
öt egymástitáni egész szám. Tehát közülük egy és csakis egy osztható 5-tel. A középső szám nem osztható 5-tel, tehát a másik négy közt kell 5-tel oszthatónak lennie. Ebből már következik a feladat állításának helyessége.
1Lásd pl. Faragú László: ≫ A számelmélet elemei≪ c. szakköri füzet 75. old.

2A primszáwoknak ez a nevezetes tulajdonsága semmiképpen sem tekinthető magától értetődőnek. Bizonyításira lásd pl. az előző lábjegyzetben idézett műben a 22. old.