Cím: Az 1955. évi Rákosi Mátyás matematikai tanulmányi verseny II. (döntő) fordulója
Füzet: 1955/szeptember, 1 - 13. oldal  PDF  |  MathML 
Témakör(ök): OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az április 23-án lefolyt II. (döntő) fordulóban az alábbi három feladat volt kitűzve:
1. Bizonyítsuk be, hogy ha n tetszőleges természetes szám, akkor

5n+2⋅3n-1+1
osztható 8-cal.
2. Határozzuk meg az
(x+y)4=6x2y2-215,xy(x2+y2)=-78
egyenletrendszer valós gyökeit.
3. Írjunk adott hegyesszögű háromszögbe téglalapokat, amelyeknek egyik oldala meghatározott háromszög oldalon (és további két csúcsa is a háromszög kerületén) van.
a) Határozzuk meg e téglalapok középpontjainak mértani helyét.
b) Írjunk az adott háromszögbe három olyan téglalapot, amelyeknek közös a körülírt körük.
 

Öt órai munka után 131 iskolából 331 dolgozatot adtak be.
A Bolyai János Matematikai Társulat által az Oktatásügyi Minisztériummal egyetértésben kiküldött Központi Bizottság május 18-án a következő jelentést fogadta el:
≫A Bizottság megállapítja, hogy a verseny, mind a versenyzők teljesítményét, mind a feladatok kiválasztását tekintve, igen sikeres volt.
A beadott dolgozatok alapján további fejlődés állapítható meg a tanulók tudásában és fogalmazásában. Szövegmentes megoldás a döntőben már nem akadt, viszont a többletmunka tekintetében további haladás volt észlelhető.
Mind a három feladat bőven adott alkalmat minőségileg értékes megoldásokra és többletmunkára. Voltak versenyzők, akik éppen a legkönnyebbnek bizonyult 1. (számelméleti) feladatot nem tudták megoldani, de boldogultak a 2. (algebrai) és 3. (geometriai) feladattal. Ez utóbbi ‐ ha a teljes, kifogástalan megoldást tekintjük ‐ bizonyult a legnehezebbnek, de ezzel is számos versenyző megbirkózott, értékes, ötletes megoldásokat adva a feladat első illetőleg második részéhez.
Mind a három feladatot megoldotta 18 versenyző. Ezek közül a megoldások minőségével, a fogalmazás szabatosságával és értékes többletmunkával kiválik 7 tanuló.
Bártfai Pál, Szabados József, Csiszár Imre az első feladathoz 3 különböző megoldást ad, a 2. feladatra Szabados ad két megoldást. Bártfai dolgozata a 3. feladat második részére, az első résztől független, igen értékes II. megoldást tartalmaz. Hasonlóképpen értékes Szabados megoldása a 3b feladatra. Csiszár pedig a 3. feladat első részére ad kétfélé megoldást.
Ezek alapján a Bizottság javasolja, hogy az 1. díjat Bártfai Pál, a budapesti Petőfi gimnázium IV. oszt. tanulónak ítéljék oda, 2. díjban Szabados József, a budapesti Árpád g. III. oszt. tanulója, 3. díjban Csiszár Imre, a budapesti Petőfi g. III. oszt. tanulója részesüljön, míg azt a négy tanulót, akinek teljesítménye nem sokkal marad el a díjnyerteseké mögött, I. dicséretre ajánlja.
Legalább három feladat megoldásáért a Bizottság II. dicséretre ajánl 11 tanulót. Két feladat megoldásán felül lényeges többletteljesítményt nyújtott 24 versenyző, míg legalább két feladatot megoldott vagy ezzel egyenértékű teljesítményt ért el 27 tanuló. A Bizottság az előbbieket III. dicséretre, az utóbbiakat pedig IV. dicséretre javasolja≪.
 

Az O. M. a fenti javaslat alapján a következő döntést hozta:
 


1. díj (oklevél + 1000 Ft)
Bártfai Pál (Bp. I., Petőfi g. IV. o. t.)
 


2. díj (oklevél + 500 Ft)
Szabados József (Bp. III., Árpád g. III. o. t.)
 


3. díj (oklevél + 500 Ft)
Csiszár Imre (Bp. I., Petőfi g. III. o. t.)
 


I. dicséretben és nagyobb könyvjutalomban részesült:
Beleznay Ferenc (Bp. VIII., Piarista g. IV. o. t.)
Biczó Géza (Bp. II., Rákóczi g. IV. o. t.)
Harza Tibor (Székesfehérvár, József Attila g. III. o. t.)
Kálmán György (Szolnok, Verseghy Ferenc g. IV. o. t.)

 


II. dicséretet és könyvjutalmat nyert:
Almási Lajos (Bp. II, Rákóczi g. IV. o. t.), Boros Pál (Bp. VII., Madách g. IV. o. t.), Kertész Ádám (Bp. I., Toldy F. g. IV. o. t.). Pátkai György (Bp. IX.,) Vértes Péter (Bp. V., Eötvös g. IV. o. t.), Zentai Árpád (Bp. XVIII., Steinmetz g. III. o. t.), Zsombok Zoltán (Bp. IV., Könyves Kálmán g. III. o. t.).
 


III. dicséretben és könyvjutalomban részesült:
Bauer András (Bp. II., Rákóczi g. IV. o. t.), Beke Gyula (Hatvan, Bajza g. III. o. t.), Benkő Bálint (Sárospatak, Rákóczi g. III. o. t.), Dominyák Imre (Miskolc, Földes g. IV. o. t.), Doroszlai Pál (Bp. I., Petőfi g. IV. o. t.), Farkas László (Ózd, József Attila g. III. o. t.), Györösi Péter (Bp. IV., Könyves Kálmán g. III. o.t.), Jakubavics Péter (Bp. V., Eötvös g. III. o. t.), Jedlovszky Pál (Bp. XIV., Petrik vegyip. techn. III. o. t.), Jónás József (Gyöngyös, Vak Bottyán g. IV. o. t.), Kiss Péter (Gyöngyös, Vak Bottyán g. IV. o. t.), Kovács István (Bp. IV., Piarista g. IV. o. t.), Lackner Györgyi (Bp. V., Bolyai textilip. techn. IV. o. t.), Lábos Elemér (Sátoraljaújhely, Kossuth g. IV. o. t.), Mecseki Attila (Bp. XV., Dózsa György g. IV. o. t.), Neumann György (Bp. XIII., Villamosenergiaip. techn. IV. o.t.), Quittner Pál (Bp. I., Petőfi g. IV. o. t.), Rázga Tamás (Bp. II., Rákóczi g. III. o. t.), Szabó Endre (Gyöngyös, Vak Bottyán g. IV. o. t.), Tarlacz László (Szombathely, Nagy Lajos g. IV. o. t.), Tolnai Tibor (Szombathely, Nagy Lajos g. IV. o. t.), Udvari András (Bp. VIII., Piarista g. III. o. t.), Uray László (Bp. VIII., Piarista g. IV. o. t.), Ványai László, (Sátoraljaújhely, Kossuth g. III. o. t.).

 


IV. dicséretben és könyvjutalamban részesült:
Beliczky Géza (Celldömölk, Gábor Áron g. IV. o. t.), Bauer Péter (Bp. VI., Kiilrsey Ferenc g. IV. o. t.), Bognár Péter (Bp. XIII., Villamosip. techn. IV. o. t.), Bokor Gábor (Bp. XIV., Gorkij isk. IV. o. t.), Boschán Péter (Bp. VIII., Széchenyi g. III. o. t.), Deák Henrik (Pécs, Szakérettségis tanfolyam), Dévai Huba (Karcag, Gábor Áron g. IV. o. t.), Dunay András (Bp. I., Petőfi g. IV. o. t.), Edőcsény LászLó (Bp. XI., József Attila g. IV. o. t.), Fuchs Tamás (Bp. II., Rákóczi g. IV. o. t.), Gerencsér Piroska (Bp. VIII., Zrínyi Ilona lg. IV. o. t.), Kirz János (Bp. VIII.. Apáczai Csere g. IV. o. t.), Kiss Sándor (Debrecen, Ref. g. III. o. t.), Krakóczki Ferenc (Gyöngyös, Vak Bottyán g. IV. o. t.), Krem Alajos (Bp. VIII., Bánki Donát gépip. techn. III. o. t.). Komjátszegi Lajos (Szeged, Irinyi vegyip. techn. IV. o. t.), Makai Imre (Csongrád, Bacsányi g. IV. o. t.). 0rlik Péter (Bp. V., Eötvös g. III. o. t.), Peták Kálmán (Ózd. József Attila g. IV. o. t.), Polgár Előd (Bp. VIII., Széchenyi g. III. o. t), Rédly Dénes (Pannonhalna, Bencés g. IV. o. t.), Roboz Ágnes (Bp. VI., Varga, Katalin IV. o. t.), Szepesszentgyörgyi Oszkár (Sátoraljaújhely, Kossuth g. IV. o. t.). Takács Gyula (Bp. VIII., Piarista g. IV. o. t.), Válas György (Bp. XIV., Gorkij isk. III. o. t.), Vértes György (Bp. XIV., Petrik vegyip. techn. IV. o. t.), Zárody Albin (Győr, Gépip. techn. III. o. t.).
*

Bár hivatalosan semmiféle pontozás nincs, szerkesztőségünk célszerűnek tartja a teljesítmények összehasonlítására a helyezéseket ‐ mint az az előbbi években is történt ‐ pontozni. Ilyen módon ez idén 7+6+5+4⋅4+11⋅3+24⋅2+27⋅1=142 pont került szétosztásra. A verseny végeredményét megyék és iskolafajuk szerint a 4. oldalon közölt táblázat mutatja.
Lapunk feladatmegoldói ez idén még az előbbi évek kítünő eredményeit is felülmúlták, amennyiben a döntőben részt vett 331 tanuló közül 146 (44,1%) volt lapunk munkatársa; a 69 helyezett közül azonban már 62 (89,91%) lapunk feladatmegoldója, akik összesen 133 pontot, azaz az összes pontok 93%-át érték el. (Részletes beszámoló ‐ sokféle szempontból ‐ a ≫Köznevelés≪ július 1-i számában a 314‐315. oldalon jelent meg.)
Kimutatás az 1955. évi Rákosi Mátyás Matematikai verseny II. fordulójáról megyék és iskolafajok szerint

 


Beadott dolgozatok száma|EredményMegyék és  gimn.ip. t.összesenDíjDicséretPontszámBudapest(nem hivatalos)isk.tan.isk.tan.  isk.tan.1.2.I.II.III.IV.V.g.ip.t.  |össz.1. Baranya2*626412------1*1*-1*2. Bács‐Kiskun51011611----------3. Békés46--46----------4. Borsod71925924-----5212-125. Csongrád5615611------2112  6. Fejér142337---1---4-47. Győr‐Sopron-81159------21128. Hajdú‐Bihar51012612------11-19. Heves381149-----419-910. Komárom41011511----------11. Nógrád111324----------12. Pest561268----------13. Somogy23--23----1--3-314. Szabolcs‐Szatmár221133----------15. Szolnok561167---1--15-516. Tolna12--12----------17. Vas51112613-----215-518. Veszprém51411615----------19. Zala11--11----------Vidék67133183585168---21111142244Budapest33122134146163111210131689998Összesen1002553176131331111411242713111142

*1 szakérettségis tanf. ill. tanuló.
 

Alább közöljük a II. forduló feladatainak megoldását.
 

1. feladat
 

Ismeretesek a következő oszthatósági tételek:
Ha n természetes szám, akkor
an-bn osztható (a-b)-vel,(1)an+bn osztható (a+b)-vel, ha n páratlan.(2)



E tételeket felhasználva többféleképpen is bizonyíthatjuk feladatunk állítását.
 

I. megoldás: Jelöljük az adott kifejezést F(n)-nel,
a) Ha n páros, vagyis n=2k (ahol k=1,2,3...), akkor írjuk F(n)-et a következő alakban
F(2k)=(52k-1)+2(32k-1+1).

A jobboldal első tagja (1) alapján osztható (52-12)=24=3⋅8-cal, a második tagban a zárójeles tényező (2) alapján osztható 3+1=4-gyel, vagyis a második tag osztható 2⋅4=8-cal.
 

b) Ha n páratlan, vagyis n=2k+1 (ahol k=0, 1, 2, ...), akkor k=0 esetén F(1)=5+2+1=8, minden más esetben pedig
F(2k+1)=52k+1-5+2⋅32k+6=5(52k-1)+6(32k-1+1).

Ez esetben tehát nemcsak az első tag osztható 24-gyel, hanem a második tag is osztható 6⋅4=24-gyel. Tehát 1-nél nagyobb páratlan n esetén, kifejezésünk nemcsak 8-cal, hanem 24-gyel is osztható.
 

II. megoldás: a) Ha n=2k (ahol k=1, 2, 3, ...), akkor F(n) így is írható:
F(2k)=5⋅52k-1+5⋅32k-1-3⋅32k-1+1==5(52k-1+32k-1)-(9k-1).


A jobboldal első tagja (2) alapján osztható 5+3=8-cal, a második tag pedig (1) alapján 9-1=8-cal.
b) Ha n=2k+1 (ahol k=0, 1, 2, ...), akkor
F(2k+1)=52k+1+(3-1)32k+1=(52k+1+32k+1)-(9k-1),
amiből az előbbi esethez teljesen hasonlóan következik, hogy F(n) osztható 8-cal.
 

Megjegyzés: Sok versenyző a kéttagúak hatványának polinom előállítását használta fel, azonban ‐ mint láttuk ‐ a kevesebb előismeretet feltételező (1) és (2) alatti oszthatósági tételek is elegendők. Még ezek is mellőzhetők, ha teljes indukciót alkalmazunk.
 

III. megoldás: n=1-re a bizonyítandó állítás igaz, mert F(1)=8.
Tegyük fel, hogy F(k) osztható 8-cal, akkor elegendő azt bizonyítani, hogy F(k+1)-F(k) is osztható 8-cal.
F(k+1)-F(k)=(5k+1+2⋅3k+1)-(5k+2⋅3k-1+1)==5⋅5k+6⋅3k-1+1-5k-2⋅3k-1-1=4(5k-1+3k-1).


A zárójeles kifejezés, mint két páratlan szám összege, páros szám, és így F(k+1)-F(k) osztható 4⋅2=8-cal.
 


2. feladat
I. megoldás:
(x+y)4=6x2y2-215,(1)xy(x2+y2)=-78(2)

(2) így is irható:
xy(x+y)2=2x2y2-78.(3)

(2) alapján xy≠0, szorozhatjuk tehát (1)-et x2y2-tel, (3)-at pedig emeljük négyzetre
x2y2(x+y)4=6x4y4-215x2y2,(4)x2y2(x+y)4=(2x2y2-78)2.(5)

(4) és (5)-ből következik, hogy a két jobboldal egyenlő. Vezessük be az x2y2=z jelölést és vegyük észre, hogy ha x és y valósak, akkor z>0.
6z2-215z=(2z-78)2=4z2-312z+6084,
vagyis
2z2+97z-6084=0,(6)
amiből a pozitív gyök
z=36.
Tehát
z=x2y2=36,
és mivel (2) alapján xy<0, azért
xy=-6.(7)

Így (3)-ból
(x+y)2=72-78-6=1,(8)
vagyis
x+y=±1.(9)
(9)-ből y=-x±1; ezt az értéket (7)-be helyettesítve
-x2+x+6=0(10)
ill.
-x2-x+6=0(11)
(10)-ből x1=3, x2=-2, (11)-ből x3=-3, x4=2, és így (7)-ből
y1=-2,y2=3,y3=2,y4=-3.

Megjegyzés: A (6) alatti egyenlethez még az alábbi módon is juthatunk.
Írjuk (1)-et a következőképpen
x4+4x3y+6x2y2+4xy3+y4=6x2y2-215,
akkor
x4+y4+4xy(x2+y2)=-215,
és így (2) figyelembevételével
x4+y4=-4(-78)-215=312-215=97.(12)
(2)-t négyzetre emelve
x2y2(x4+y4+2x2y2)=6084.
(12) figyelembevételével és x2y2 helyébe z-t írva a (6) egyenlethez jutunk.
 

II. megoldás: Legyen (x+y)2=u és xy=v, akkor x2+y2=(x+y)2-2xy=u-2v, és egyenletrendszerünk így alakul
u2-6v2+215=0,(1)v(u-2v)+178=uv-2v2+78=0.(2)

Vegyük észre, hogy ha x és y valósak, akkor u≥0. (2) háromszorosából (1)-et kivonva
3uv-u2+19=0,
ahonnan
v=u2-193u.(3)
Ezt az értékét (1)-be helyettesítve
u2-6u4-38u2+3619u2+215=0,
amiből
u4+721u2-722=0,
és innen az egyetlen pozitív gyök
u=1.
(3)-ból
v=1-193=-6.
Tehát
x+y=u=±1,xy=v=-6.



Tovább úgy történhetik a számítás, mint az I. megoldásban.
 

III. megoldás: Felhasználva az I. megoldás (12) alatti
x4+y4=97,
valamint az előző megoldásokból az
x2y2=36,
azaz
x4y4=1296
egyenleteket, látjuk, hogy x4 és y4 a
t2-97t+1296=0
másodfokú egyenlet két gyöke; ezek pedig
t1=81,t2=16.
Tehát
x4=81ésy4=16,vagy fordítvax4=16ésy4=81,
ahonnan (xy<0 figyelembevételével) az előbbi megoldásokban szereplő négy valós gyökpár adódik.
 


3. feladat a) része
 

I. megoldás: Vizsgáljuk meg az ABC▵ BC=a oldalán nyugvó beírt téglalapok középpontjainak mértani helyét. Legyen egy ilyen téglalap P1P2P3P4. A betűzést az 1. ábra mutatja.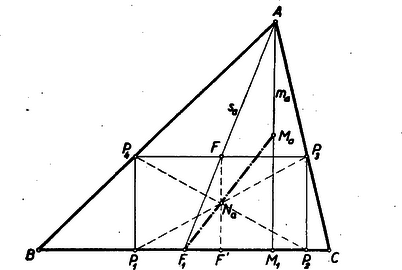
 
 
1. ábra
 

A P3P4 oldal F felezőpontja, mint ismeretes, rajta van az AF1=sa súlyvonalon. FF' a téglalap P1P2 oldalára merőleges (tehát az AM1 magasságvonallal párhuzamos) középvonala. A téglalap Na középpontja e középvonal felezőpontja, és így rajta van az AM1F1 derékszögű háromszög F1Ma súlyvonalán, ahol Ma az AM1=Ma magasság felezőpontja.
 

Megfordítva legyen Na az F1Ma szakasz tetszés szerinti belső pontja.Tegyük fel, hogy a háromszög nem egyenlőszárú. Húzzunk az Na ponton át az a egyenesre merőleges egyenest, legyen ennek az a és az AF1 egyenesek közé eső szakasza F'F. Ennek Na felezőpontja, mert az AF1M1 háromszög F1Ma súlyvonalán van és F'F párhuzamos az ABC háromszög AM1 magasságával. Hasonlóan látható, hogy az F pont felezi a rajta át a-val párhuzamosan húzott egyenesnek az AC és AB vonalak közé eső P3P4 szakaszát. A végpontokból az a egyenesre P3P2 és P4P1 merőlegeseket bocsátva tehát olyat téglalapot kapunk, amelynek Na a középpontja és amely az ABC háromszögbe van írva a kívánt módon. Több ilyen téglalap nem lehetséges, mert ha a P3P4 oldalt közelítjük az a oldalhoz, illetőleg távolítjuk attól, akkor a középpont is közeledik, illetőleg távolodik, tehát különbözni fog Na-tól.
 

Ha az ABC háromszög egyenlőszárú (AB=AC), akkor a szimmetria alapján könnyen látható (2. ábra), hogy a téglalapok középpontjai az M1Ma szakaszra esnek, másrészt ennek bármely Na belsőpontjára tükrözve az M1(=F1) pontot, az F tükörképen át a-val párhuzamosan húzott egyenesnek a szárakkal való metszéspontjaiból az a oldalra bocsátott merőlegesek ismét egy kívánt tulajdonságú téglalapot adnak.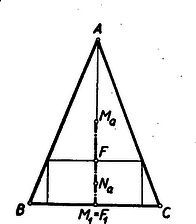
 
 
2. ábra
 

Az F1 és Ma végpontokhoz tartozó téglalapok az a oldallá, illetőleg az Ma magasságvonallá fajulnak.
A keresett mértani hely tehát az F1Ma szakasz.
 

II. megoldás: A téglalap középpontja felfogható a másik, P1P2-vel párhuzamos, FbFc középvonal felezőpontjaként is (3. ábra).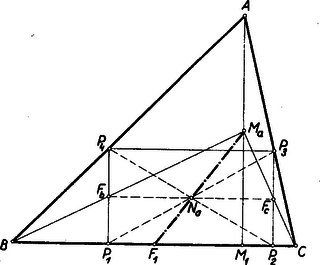
 
 
3. ábra
 

Nyilvánvaló, hogy Fb, mint P1P4 felezőpontja rajta van az AM1B derékszögű háromszőg BMa súlyvonalán, Fc pedig az AM1C háromszög CMa súlyvonalán. Így az FbFc középvonal Na felezöpontja rajta van a BMaC▵-nek MaF1 súlyvonalán.
Ismét könnyen látható a gondolatmenet megfordításával, hogy az F1Ma szakasz minden pontjához tartozik pontosan egy kívánt elhelyezkedésű téglalap, amelynek a kiszemelt pont a középpontja.
*

Mint a fenti két megoldásból látható, a keresett mértani hely teljesen elemi úton, minden koordináta‐geometria nélkül meghatározható. Minthogy igen sok versenyző használt koordináta‐geometriát, mégpedig legtöbbnyire igen ügyetlenül, és gyakran még a helyes eredménynek sem tudott geometriai értelmet adni, azért itt közlünk egy egyszerű megoldást koordináta‐geometriában.
 

III. megoldás: Helyezzük el hegyesszögű háromszögünket a derékszögű koordinátarendszerben úgy, hogy a BC oldal az x tengelyre, az A csúcspont a pozitív tengelyre kerüljön. A betűzést a 4. ábra mutatja.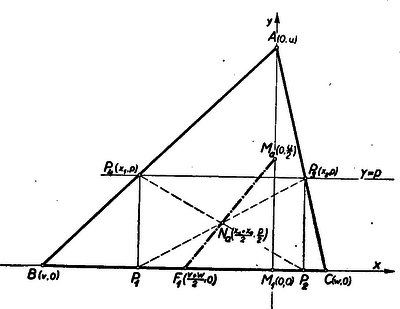
 
 
4. ábra
 

Legyen a P3P4 téglalapoldal egyenlete y=p, a P4 pont koordinátái (x1,p) és P3 ponté (x2,p) akkor Na, a téglalap középpontjának koordinátái xa=x1+x22, ya=p2.
 

Az AB egyenes egyenlete
y=-uvx+u,azazux+vy=uv,(1)
Az AC egyenes egyenlete
y=-uwx+u,azazux+wy=uw,(2)
y helyébe a P3 illetőleg P4 pont p ordinátáját írva, (1)-ből, illetőleg (2)-ből x értékül x1-et, illetőleg x2-t kell kapnunk, tehát
ux1+vp=uvésux2+wp=uw.

A kettőt összeadva
u(x1+x2)+(v+w)p=u(v+w)

Mivel x1+x2 és p az Na pont xa és ya koordinátáinak kétszeresei, így azt kaptuk, hogy e koordinátákra
2uxa+2(v+w)ya=u(v+w),(3)
vagyis (explicit alakra térve át) Na koordinátái kielégítik az
y=-uv+w(x-v+w2)
egyenletet, feltéve, hogy v+w≠0.
Ez az egyenes átmegy a (v+w2,0) ponton, vagyis a BC oldal F1 felezőpontján, és iránytangense -uv+w=-u2:v+w2, de ez nem más, mint F1-ből a (0,u2) pontba, a magasságvonal Ma felezőpontjába vivő egyenes iránytangense. Az Na pont tehát ezen az egyenesen mozog, és mivel p pozitív és u-nál kisebb, így ya pozitiv és u2-nél kisebb, xa pedig v+w2 és 0 között változik, mert ya két szélső érlékéhez xa=v+w2 (ha ya=0), illetőleg xa=0 (mikor ya=u2) értékek tartoznak.
A keresett mértani hely tehát az F1Ma szakasz.
Ha v+w=0, vagyis egyenlőszárú a háromszög, akkor (3)-ból
xa=0,
továbbá most is 0<ya<u2. A mértani hely tehát most is az F1Ma(=M1Ma) szakasz.
 

Megjegyzés: Ha megengedjük, hogy a beírt téglalapok csúcspontjai a háromszögoldalak meghosszabbításán is lehetnek, akkor a háromszög tompaszögű is lehet, és a mértani hely a teljes F1Ma egyenes.
 


3. feladat b) része
 

I. megoldás: A téglalap köré írt kör középpontja a téglalap középpontja, a téglalap átlója pedig átmérője a körnek. Így a keresett téglalapok középpontjának közösnek kell lennie, átlóiknak pedig egyenlőknek ‐ ha vannak egyáltalán ilyen téglalapok.
Két téglalap közös középpontja a feladat a) része szerint csak két háromszögoldalhoz meghatározott mértani helyek közös pontja lehet. Mivel az adott háromszög feltétel szerint hegyesszögű, a magasságvonalak Ma, Mb, és Mc felezőpontjai az oldalközéppontok alkotta F1F2F3 háromszög oldalainak belső pontjai (5. ábra), az F1Ma és F2Mb szakaszok tehát e háromszög transzverzálisai, s így metszik egymást egy N pontban.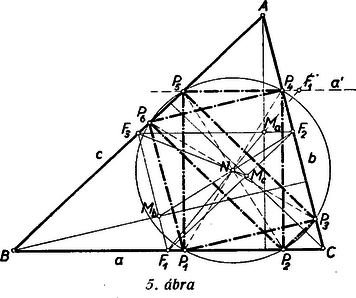
 
 
5. ábra
 

Legyen az ABC háromszögbe írt N középpontú és a oldalon nyugvó téglalap P1P2P4P5. Tudjuk, hogy van ilyen téglalap és csak egy.
A P1 és P4 pontok, mint átlóvégpontok, egymás tükörképei az N pontra vonatkozóan. Mivel pedig a b egyenesnek csak egy olyan pontja van, amelynek N-re vonatkozó tükörképe a BC egyenesen van, így P4 ez a pont.
Az N pont rajta van az F2Mb egyenesen is, tehát írható az ABC háromszögbe olyan N középpontú téglalap is, amelyik a b oldalon nyugszik. Ennek egyik b-n levő csúcsával átellenes csúcs az a oldalon lesz és ezek egymás tükörképei az N pontra nézve, így az előző megjegyzés szerint e csúcspárt csak a P4 és P1 pontok adhatják. Legyen a kérdéses b oldalon nyugvó beírt téglalap P3P4P6P1. Ekkor a P3P6=P1P4, mint a téglalap átlói, továbbá P1P4=P2P5, mint a P1P2P4P5 téglalap átlói. Mindhárom átlót felezi az N pont.
Ekkor a P5P6P2P3 négyszög átlói is felezik egymást és egyenlők, tehát a négyszög téglalap; az ABC háromszögbe írt olyan téglalap, amelynek N a középpontja és egyik oldala az AB=c háromszögoldalon van. A három téglalap középpontja közös, átlóik egyenlők, tehát körülírt körük közös.
A feladat a) része I. megoldásának második felét is figyelembe véve, a fenti gondolatmenet módot ad a téglalapok megszerkesztésére is (5. ábra). Ilyen téglalap‐hármas csak egy lehet, mert az N pont egyértelműen meg van határozva, ennek helyzete pedig egyértelműen meghatározza a téglalapokat.
Mivel N középpontja mindhárom téglalapnak, eredményünkből az is következik, hogy az F1Ma, F2Mb, F3Mc mértani helyek egy ponton mennek keresztül.
 

II. megoldás: A mértani helyek felhasználása nélkül is megoldható feladatunk. Ha a P1P3P5▵-et tekintjük (5. ábra), akkor látjuk, hogy a P1-nél levő szög, mint merőleges szárú szög, egyenlő az ABC▵-nek C-nél fekvő γ szögével. Ugyanezen oknál fogva a P1P3P5∢=α, és P3P5P1∢=β, és így
P3P5P1▵∼ABC▵.

A P6P2P4 háromszög a P3P5P1 háromszögnek a köréjük írt kör középpontjára vonatkozó tükörképe. Ezt a megfigyelést felhasználva a következőképpen szerkeszthetünk a keresett ábrához hasonlót (amit azután alkalmasan elforgatva és kicsinyítve már könnyen megszerkeszthetjük a keresett téglalapokat).
Rajzoljunk az ABC▵ köré kört; ebben a csúcsokkal átellenes pontok legyenek A', B', C' (6. ábra).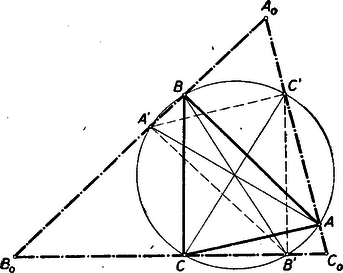
 
 
6. ábra
 

Az AC', BA', CB' egyenesek alkotta A0B0C0▵ oldalai merőlegesek az ABC▵ megfelelő oldalaira, s így a két háromszög hasonló. ABA'B', BCB'C' és CAC'A' az előbbi háromszögbe beírt téglalapok, mert átlóik (mint körátmérők) felezik egymást és egyenlők. Így valóban a keresett ábrához hasonlót nyertünk. (Magát a szerkesztést természetesen mindjárt az A0B0C0▵ megrajzolásával kezdhetjük; a szerkesztés igazolását szolgáló segédvonalak a szerkesztéskor elhagyhatók).
 

III. megoldás: A P1, P6, P5 és P4 pontok ismeretében (5. ábra) a másik kettő könnyen szerkeszthető (pl. mint P6 és P5 tükörképe a P1P4 szakasz felezőpontjára). E négy pont viszont P1 ismeretében úgy szerkeszthető, hogy belőle a-ra merőlegest állítunk, illetőleg b-vel párhuzamost húzunk. Az előbbinek c-vel való P6 metszéspontjából párhuzamost húzunk a-val, az utóbbinak c-vel való P6 metszőpontjából merőlegest állítunk b-re. A kettő P4-ben metszi egymást.
 

Ha egy pontot sem ismerünk, akkor az a oldal tetszésszerinti Q1 pontjából kiindulva végezzük el az éppen leírt szerkesztést, a keletkezett metszéspontok legyenek sorra Q5, Q6, Q4 (7. ábra).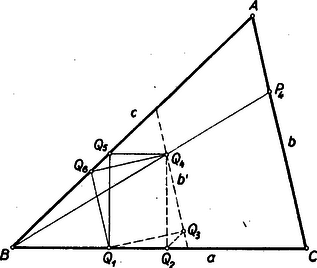
 
 
7. ábra
 

Egészítsük ki Q6Q5Q4-et egy Q2 csúccsal, Q1Q6Q4-et pedig egy Q3 csúccsal téglalappá. Q2 nyilván a-n van, a Q3-an és Q4-en átmenő b' egyenes pedig párhuzamos b-vel. A keletkezett téglalapok Q2Q5, illetőleg Q3Q6 átlói egyenlők a közös Q1Q4 átlóval és felezik egymást annak felezőpontjában. Ebből viszont következik, hogy Q5Q6Q2Q3 is téglalap, mert átlói felezik egymást és egyenlő hosszúak. Az a, b' és c oldalak az adott háromszöghöz hasonló és hasonló helyzetű háromszöget alkotnak B-vel mint hasonlósági ponttal. Így a keresett ábrához hasonlót kaptunk. Q4-et B-ből b-re vetítve nyerjük a P4 pontot és ebből kiindulva már megszerkeszthetjük a továbbiakat. (A szerkesztés elvégzésekor Q4 után természetesen mindjárt P4-et szerkesztjük. A szerkesztés megtalálását és egyben mindjárt helyességének igazolását is szolgáló segédvonalak és pontok megrajzolására a szerkesztéskor nincs szükség.)
 

Megjegyzések: 1. A feladat a) részéhez fűzött megjegyzésből kitűnik, hogy ha a beírt téglalap csúcspontjaira semmi kikötést nem teszünk, akkor tompaszögű háromszög esetén is megoldható feladatunk b) része.
2. Derékszögű háromszög esetén (pl. ha γ=90∘) F1≡Mb és F2≡Ma, és így Mc≡N, P5≡P6, P2≡P3≡C. Ez esetben tehát a befogókhoz tartozó téglalapok azonosak, az átfogóhoz tartozó téglalap pedig az mc magasságvonallá fajul.
3. Tehát minden háromszögnek van egy és csakis egy N pontja.