Cím: A Menelaos- és a Ceva-féle tétel
Szerző(k):  Kárteszi Ferenc 
Füzet: 1955/november, 67 - 75. oldal  PDF  |  MathML 
Témakör(ök): Szakmai cikkek
Hivatkozás(ok):Feladatok: 1955/november: 307. matematika gyakorlat, 1955/november: 308. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Menelaos- és a Ceva-féle tétel1

 

1. A lineáris ponthármas osztóviszonya

 

Három, egy egyeneshez illeszkedő pont konfigurációját (vagyis azt az alakzatot, melyet ilyen három pont alkot) lineáris ponthármasnak nevezzük. Ez a geometriai fogalom ‐ ha nem is a mondott nevén nevezve ‐ előfordul a középiskolai tananyagban is. Néhány példát megemlítünk.
A háromszög bármelyik szögpontja, a vele szemközti oldal felezőpontja, a háromszög súlypontja lineáris ponthármast alkotnak, mégpedig a szóbanforgó szögponthoz tartozó súlyvonalon. Ilyen pl. az 1. ábrán az 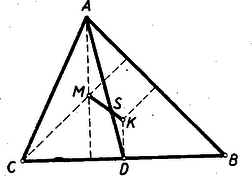A,D,S.
 
 
1. ábra
 

Az S pont az AD szakaszt 2:1 arányban osztja. Ilyen továbbá a háromszög köré írt kör középpontja (K), magasságpontja (M), súlypontja (S) által alkotott ponthármas is. Ezeket a pontokat az Euler-féle egyenes köti össze, vagyis ugyancsak lineáris ponthármast alkotnak. Itt most az S pont a KM szakaszt 1:2 arányban osztja. Az eddig mondottak mintájára a D pont BC szakaszon való helyét is kifejezhetnők úgy, hogy az a pont, mely a BC szakaszt 1:1 arányban osztja.
A felsorolt példák mutatják a következő fogalmak és jelölések bevezetésének célszerűségét. Akkor, de csak akkor, ha A,B,X egy egyenes három különböző pontja, (ABX)-szel jelöljük az AX és XB távolság hányadosát. Az
(ABX)=AXXB
távolság-hányadost az X osztópont A és B alappontokra vonatkozó osztóviszonyának nevezzük. Így ‐ hacsak X nem az AB szakasz felezőpontja ‐ az (ABX) és (BAX) osztóviszony két különböző szám. A definícióban adott hányados alakból tüstént láthatjuk, hogy az utóbbi az előbbinek reciprok értéke. Ezért az írás sorrendjében első és második alappontról beszélünk. Azt nem kötjük ki, hogy X az AB szakasz valódi osztópontja (belső pontja) legyen, lehet az AB szakasz B-felé, avagy A felé való meghosszabbításán is (külső pont). Éppen ezért szerencsésebb X-et ‐ általában ‐ viszonyított pontnak nevezni.
További meggondolásra int a következő ‐ ugyancsak jól ismert ‐ tétel. A háromszög bármelyik szögpontjához tartozó szögfelezők (akár belső, akár külső szögfelező) egyező osztóviszonyú pontokban metszik a szögponttal szemközti oldalt (2. ábra).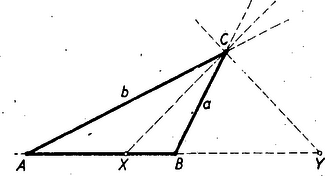
 
 
2. ábra
 

Az idézett tétel a bevezetett jelöléssel így fejezhető ki:
(ABX)=baés(ABY)=ba

Jegyezzük meg azt a kivételes esetet, amidőn a=b, mert akkor
(ABX)=1:1,
de az (ABY)-nak nincs értelme, mert a C-hez tartozó külső szögfelező BC oldalegyenessel párhuzamos, tehát Y metszéspont nem is lép fel. No már most, ha az osztóviszony felírt jelöléséből és az ahhoz tartozó értékből kívánjuk az alappontokat összekötő egyenesen a viszonyított pont helyét rekonstruálni, még azt sem tudjuk, hogy belső, vagy külső pontról van-e szó; hiszen éppen az idézett tétel felírásából láttuk, e feladat nem egyértelmű.
A most mondottak indokolják az osztóviszony értékének előjellel való ellátását. Tekintsük az AX-et és XB-t úgy, hogy A-tól X felé és X- től B felé haladva leírt utakról van szó. Az AB szakasz belsejébe eső X-re nézve ezek az utak egyező irányításúak, a szakasz meghosszabbítására eső X esetében ellenkező irányításúak. Az utóbbi esetben tekintsük az osztóviszonyt negatív számnak. Így a 2. ábrára vonatkozó állításunk szerencsés kifejezése:
(ABX)=+baés(ABY)=-ba.

Annyiban módosítjuk tehát az (ABX) eredeti értelmezését, hogy az AX:XB hányadost irányított utak hányadosának tekintjük és ezáltal az osztóviszony előjeles számot szolgáltat2.
Az AB egyenest leíró X pont (ABX) osztóviszonya az X mozgása folyamán folytonosan változik és egy rögzített X helyhez egy határozott (ABX) érték tartozik3. Kivételt képez az A-val egybeeső és a B-vel egybeeső X pont, ahol is a három különböző pontot feltételező (ABX) értelmezése hiányzik.
Ha pedig adva van A és B, továbbá egy v szám akkor az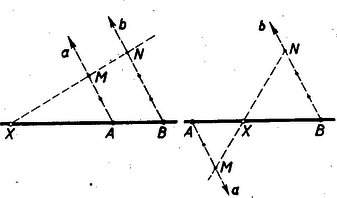
(ABX)=v
kirovásnak megfelelő X pont egyértelműen előállítható. A 3. ábra a v=-2/3 és v=+2/3 értéknek megfelelő eljárást mutatja be. Szóban csak annyit fűzünk hozzá, hogy a és b tetszőleges, de egymással párhuzamos segédegyenesek.
 
 
3. ábra
 

Mérjük fel az a és b segédegyenesekre A-tól M-ig terjedően és B-től N-ig terjedően egy tetszőlegesen választott szakasznak 2-szeresét 3-szorosát.
Az eljárás alkalmazható tetszés szerinti v érték esetén. Általában AM és BN szerepét olyan szakaszokra ruházzák át, amelyeknek a hányadosa v abszolútértéke4
Ez az eljárás megvilágítja azt, hogy X metszéspont nem lép fel, ha v=-1, mert akkor AM=BN, s ennélfogva MN egyenes az AB egyenessel párhuzamos. Megvilágítja azt is, hogy v=0 esetén ‐ AM-et zérussá zsugorodott hosszúságúnak tekintve ‐ X az A-val egybeesik. (Ámde az osztóviszony fogalmát ezzel kiterjesztettük, mert eredetileg megköveteltük, hogy A,B,X különböző pontok legyenek. Nem terjeszthető ki ilyen módon a B-vel egybeeső X-re is. mert akkor a b segédegyenesre felmért osztótávolság ‐ a BN szakasz ‐ válik zérussá, osztó pedig nem lehet zérus.)
Foglaljuk össze az eddig tárgyaltak lényegét. ‐ (1) Az adott A,B pontokat összekötő egyenest leíró X pont meghatározta (ABX)=v számot tekintve: Az X pont az egyenes minden helyén ‐ kivéve a B pontot ‐ egy-egy v számot létesít. Könnyen belátható, hogy így két különböző pont két különböző számot létesít. ‐ (2) Az adott A,B pontokat összekötő egyenest és a minden értéken egyszer végigfutó v számot tekintve: Bármely v számhoz egy-egy X pont tartozik, v=-1 kivételével; két különböző számhoz két különböző pont tartozik. (3) B alappontot és v=-1 számot kivéve az (ABX)=v követelmény az AB egyenes pontjai és a számok összessége között egy egyértelmű megjeleltetést létesít.
 

2. A Menelaos-féle tétel

 

Az osztóviszony előjelzése indokolja, hogy egy egyenes szakaszainak, vagy párhuzamos egyenesű szakaszoknak az egymáshoz való viszonyítása helyett irányított ‐ vagyis kezdőponttól végpontig haladó ‐ utak hányadosát alkalmazzuk. Ilyen módon előjeles számok fognak az arányok szerepében fellépni. Aszerint, hogy egyező, vagy ellenkező irányításúak a szakaszok, a szakaszok arányát pozitív, vagy negatív számnak tekintjük.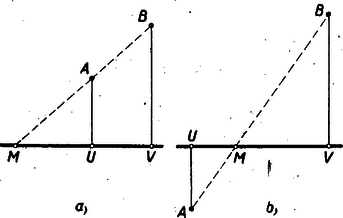
 
 
4. ábra
 

Például (4. ábra) a következő kifejezések a helyesek:
4a  ábrán  (ABM)=AUVB=UABV,4b  ábrán  (ABM)=AUBV=UAVB.
Ugyanis, ha a baloldali osztóviszony negatív, akkor a jobboldalon ellenkezően irányított, párhuzamos szakaszokat kell írnunk. Ha a baloldali osztóviszony pozitív, akkor a jobboldalon egyező irányítású, párhuzamos szakaszokat kell írnunk.
Ezzel a megállapodással az előjelzés folytán támadható logikai zavarokat elhárítottuk. A párhuzamos szelőkre vonatkozó ismert tételeinket is ebben az értelemben ‐ módosított fogalmazásban ‐ alkalmazzuk a továbbiakban.
Egy háromszög és egy a háromszög síkján levő egyenes ‐ ABC és s ‐ ha az egyenes nem megy át egyik szögponton sem, két különböző kölcsönös helyzetben lehet. A szögpontok az egyenes egyik oldalára esnek, vagy kettejük az egyik oldalára és a harmadik a másik oldalára. Eszerint, ha s az ABC mindhárom oldalegyenesét metszi, mégpedig AB, BC, CA, egyenest rendre Z, X, Y pontban, akkor az
(ABZ),(BCX),(CAY)
osztóviszonyok közül vagy három negatív, vagy kettő pozitív és egy negatív. Akár az előbbi, akár az utóbbi eset áll fenn, mindig az
(ABZ)⋅(BCX)⋅(CAY)<0
érvényes. A Menelaos-féle tétel ennél többet mond, nevezetesen azt, hogy e három osztóviszony szorzatának mi az értéke.
Menelaos-féle tétel: Ha s egyenes nem megy át az ABC háromszög egyik szögpontján sem, és az AB, BC, CA, egyeneseket rendre Z, X, Y pontokban metszi, akkor
(ABZ)⋅(BCX)⋅(CAY)=-1.

Az 5. ábra a két különböző helyzetviszonyt szemlélteti. Egy-egy oldalegyenes és az s egyenes egy-egy párt alkot. E három egyenespár bármelyikének két-két párhuzamos szelője lép fel az ábrán.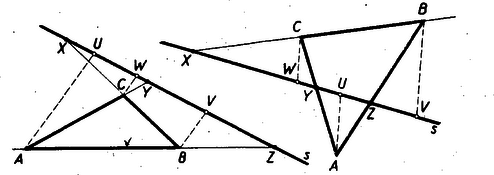
 
 
5. ábra
 

Azokra a fentebb már idézett tételt alkalmazva mind a két esetben az
(ABZ)=AUVB,(BCX)=VBCW,(CAY)=CWUA
érvényes.
A három egyenlőség szorzatából éppen a bizonyítandó formula helyessége adódik. A jobboldali törtek szorzata ugyanis >>-<< előjelű tört, melynek számlálójában és nevezőjében ugyanaz a három irányított szakasz szerepel. Tehát a jobboldal értéke valóban -1.
A Menelaos-tétel megfordításának tekinthető tétel a következő: ha az ABC háromszög szögpontjaitól különböző Z, X, Y pontok rendre az AB, BC, CA egyenesen vannak és fennáll az
(ABZ)⋅(BCX)⋅(CAY)=-1,
akkor az X, Y, Z pontok egy egyenesen vannak, vagyis X, Y, Z kollineáris ponthármas.
E tétel bizonyítását úgy végezzük, hogy a tétel állítását tagadjuk, s a Menelaos-féle tételre támaszkodva megmutatjuk a tagadás tarthatatlanságát.
Tegyük hát fel, hogy a bizonyítandó tétel összes kirovásai teljesülnek, s mégsem kollineáris az X,Y,Z ponthármas. Ennélfogva XY egyenes egy a Z-től különböző P pontban metszi az AB egyenest, vagy párhuzamos vele. Ha az első feltevés áll fenn, akkor a Menelaos-féle tétel szerint
(ABP)⋅(BCX)⋅(CAY)=-1,
a kiinduló feltevés pedig
(ABZ)⋅(BCX)⋅(CAY)=-1
volt. E kettő egybevetéséből
(ABP)=(ABZ)
következik, ami képtelenség, mert különböző pontok osztóviszonya nem lehet egyenlő. Ha a másik feltevés áll fenn, vagyis XY az AB-vel párhuzamos, akkor a párhuzamos szelők tétele szerint
(BCX)⋅(CAY)=+1,
amit a kiinduló feltevéssel egybevetve (ABZ)=-1 adódik. Ez szintén képtelenség, mert ‐ amint már tudjuk ‐ v=-1 osztóviszonynak megfelelő pont az AB egyenesen nincs.
Ezzel a megfordított tétel indirekt bizonyítását be is fejeztük.
 

3. A Ceva-féle tétel

 

Tekintsük a sík ABC háromszögét, továbbá a csúcsoktól különböző és az oldalegyenesekhez sem illeszkedő S pontot. Két esetet különböztessünk meg: az S pont a háromszög belsejében van, vagy a háromszögön kívülre esik. Tekintsünk el ama esetektől, midőn csak egyike is bekövetkezik a következő lehetőségeknek: AS∥BC, BS∥CA, CS∥AB. Másszóval AS a BC-t, BS a CA-t, CS az AB-t messe, mégpedig rendre egy X, Y, Z pontban.
Könnyen belátható az, hogy az ABC háromszög belsejében levő S pont esetében X metszéspont a B és C pontok között, Y a C és A, Z az A és B között van. Ha azonban az S külső pont és az X,Y,Z metszéspontok mind fellépnek, az oldalegyeneseken való helyzetük megállapítása körültekintőbb meggondolást kíván (6. ábra).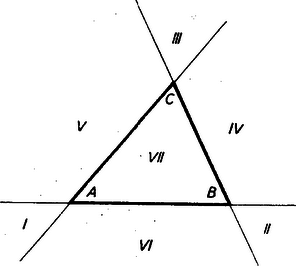
 
 
6. ábra
 

A háromszög oldalegyenesei 7 tartományra bontják a síkot. Egy véges tartományra (VII) és még hat, végtelenbe nyúló tartományra. Az utóbbiak a külső tartományok. Alkatuk szerint két különböző típust képeznek. Az egyik típushoz az I, II, III tartományok, a másikhoz a IV, V, VI tartományok tartoznak.
Ha S pont I-ben van, akkor X a B és C között Y és Z pedig rendre a CA, és AB oldal meghosszabbításán van. Ha S pont a IV tartományban van és Y, Z metszéspontok fellépnek, akkor X és B és C között, az Y és Z pedig rendre az AC és AB oldal valamelyik meghosszabbításán van. Hasonlóan tisztázható a II, III, ill. az V, VI tartományban levő S pont esetében az X,Y,Z pontok helyzete.
Az eddig megállapítottak alapján, ha S az ABC-hez képest belső pont, akkor (ABZ), (BCX), (CAY) osztóviszonyok mindegyike pozitív szám; ha pedig külső pont, akkor a három osztóviszony ketteje negatív és egy pozitív szám. Vagyis akár belső, akár külső pontra nézve, ha X, Y, Z metszéspontok mindegyike fellép, fennáll az
(ABZ)⋅(BCX)⋅(CAY)>0
egyenlőtlenség. Ceva szerint azonban ennél többet is tudunk mondani.
Ceva-féle tétel: Ha az ABC háromszög BC, CA, AB oldalegyenesein rendre X, Y, Z háromszög csúcsaitól különböző olyan pontok, hogy AX, BY, CZ egyenesek egy S pontban találkoznak, akkor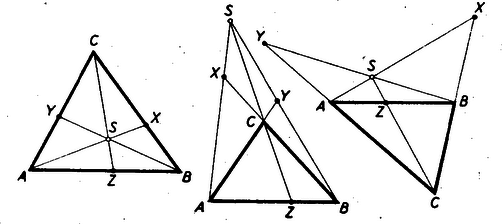
(ABZ)⋅(BCX)⋅(CAY)=+1.

 
7. ábra
 

Bizonyítás (7. ábra). Alkalmazzuk a Menelaos-féle tételt a ZCA háromszög BY szelőjére, valamint a BCZ háromszög AX szelőjére. A tételt képező egyenlőséget mindkét esetben részletes alakban írjuk ki:
ZSSC⋅CYYA⋅ABBZ=-1,ésBXXC⋅CSSZ⋅ZAAB=-1.
E két egyenlőség szorzatából, ha még az irányított szakaszokra érvényes
ZSSZ=-1,CSSC=-1,ZABZ=AZZB
egyenlőségeket is tekintetbe vesszük, éppen a bizonyítandó
AZZB⋅BXXC⋅CYYA=+1
adódik.
Ez a tétel úgy fordítható meg, hogy ha az ABC háromszög AB, BC, CA, oldalegyenesein rendre rajta vannak a csúcspontoktól különböző Z, X, Y pontok és fennáll az
(ABZ)⋅(BCX)⋅(CAY)=+1
egyenlőség, akkor az AX, BY, CZ egyenesek vagy egy pontban találkoznak, vagy párhuzamosak egymással.
A tételt itt is a tételt tagadó állítás megcáfolásával igazoljuk.
Tegyük fel, hogy AX és BY egy S pontban metszik ugyan egymást, de CZ egyenes már nem megy át az S ponton. Eszerint CS egyenes vagy egy a Z-től különböző P pontban metszi az AB oldalegyenest, vagy párhuzamos vele.
Ha fellép a P metszéspont, akkor a Ceva-féle tétel szerint
(ABP)⋅(BCX)⋅(CAY)=+1;
ezt a bizonyítandó tétel kirovásával egybevetve
(ABZ)=(ABP)
következik. Ez azonban képtelenség, mert két különböző ponthoz, ugyanazokra az alappontokra vonatkoztatva, különböző osztóviszony tartozik.
Ha pedig CS∥AB, akkor az X ponton átmenő BC és AS, valamint az Y ponton átmenő AC és BS egyenesek párhuzamos szelői a CS és az AB egyenesek. Így a párhuzamos szelőkre vonatkozó arányossági tételt alkalmazva:
BXXC=BASC,CYYA=SCAB.
Tekintetbe véve BA=-AB összefüggést is, a két egyenlőség szorzata:
BXXC⋅CYYA=-1.
Ezt az alapkirovással egybevetve következik, hogy
(ABZ)=-1.
Ez pedig képtelenség, mert ‐ amint már tudjuk ‐ a v=-1 osztóviszonyhoz nem tartozik viszonyított pont.
Annak a bizonyítása pedig, hogy ha állnak a tétel kirovásai, de az AX BY, CZ egyenesek bármely ketteje nem metszi, egymást, vagyis párhuzamosak, akkor a harmadik is párhuzamos velük, már könnyen megy, az olvasóra bízzuk.
 

4. A harmonikus pontnégyes

 

Tekintsük A,B,C,D pontokat a síkon, ha közülük semelyik három sem esik egy egyenesbe (8. ábra).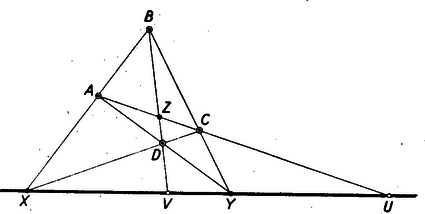
 
 
8. ábra
 

Az ilyen négy pont ún. teljesnégyszöget létesít. A teljesnégyszög szögpontokból és oldalakból álló alakzat; szögpontjai az A,B,C,D pontok és oldalai az AB, CD, AC, BD, AD, BC, egyenesek.
Bármelyik oldalnak van egy átellenes párja. Az oldal két szögpontot köt össze, az átellenese pedig a többi két szögpontot. Így az átellenes oldalak párokat alkotnak:
AB  párja  CD,AC  párja  BD,AD  párja  BC.

A párok egy-egy metszéspontot szolgáltatnak ‐ ha csak nem párhuzamosak ‐ az X,Y,Z pontokat. Ezeket átlóspontoknak nevezzük.
Tekintsünk most egy három átlósponttal rendelkező teljesnégyszöget, amilyen az ábrán is szerepel. Az XY egyenest az X,Y, átlóspontokon át nem menő AC és BD oldalak úgy metszik U és V pontokban, hogy az X,Y alappontokra és U,V viszonyított pontokra nézve fennáll az
(XYU)(XYV)=XUUY:XVVY=-1(H)
összefüggés. Úgy mondjuk e relációnak megfelelő egyenesvonalú pontnégyes viszonyát, hogy az X,Y; U,V pontpárok harmonikus pontnégyest alkotnak. Bizonyítsuk is be a (H) reláció helyességét.
Tekintsük evégből az XYB háromszöget, a d egyenest és a D pontot. Alkalmazzuk ezekre az elemekre a Menelaos-féle és a Ceva-féle tételt:
(XYU)⋅(YBC)⋅(BXA)=-1
és
(XYV)⋅(YBC)⋅(BXA)=+1.
(A háromszög oldalait d egyenes U,C,A pontokban metszi. D pontot pedig a háromszög csúcsaival összekötő egyenesek a szemközti oldalakból kimetszik a V,C,A pontokat.) E két egyenlőség hányadosaként éppen a bizonyítandó egyenlőség adódik.
A középiskolai matematika és fizika tananyagában több helyütt szerepel harmonikus pontnégyes. Így pl. ha AC=BC, akkor az ABC háromszög AB oldalát a C-nél levő szög külső és belső felezőegyenese olyan pontpárban metszi, mely az A,B alappontpárral együtt harmonikus négyest alkot. pl. a 2. ábrán az A,B;X,Y pontnégyes. Más példa: ha kisnyílású homorú gömbtükörnek középpontja (vagyis a tükröző gömbsüveg középpontja) G, a gömb középpontja O, a GO tengely, tetszőleges T pontjának képe K, akkor a G,O alappontpár a T,K pontpárral együtt harmonikus négyest alkot.
Tekintsük a számegyenesen a
0,1k-1,1k,1k+1
számokat képviselő pontokat. Vegyük alappontoknak az első és harmadik pontot, viszonyított pontoknak a negyedik és a második pontot. Rövid számolással az derül ki, hogy ezek is harmonikus pontnégyest alkotnak. Ebből érthető az is, hogy miért nevezik az
11,12,13,14,15,...
(0-hoz tartó) számsorozatot harmonikus sorozatnak,
 

Az osztóviszony, valamint a harmonikus pontnégyes fogalma, továbbá a Ceva- és a Menelaos-féle tétel, valamint e tételek megfordítottja több, sorrakövetkező feladat megoldásához fogja segíteni az olvasót.
1Menelaos az 1. században élt, görög matematikus. G. Ceva (kiejtése: Cseva) olasz matematikus, a szóban forgó tétele 1678-ból való.

2 Tisztán konvenció, hogy melyik hányadost vesszük pozitív, ill. negatív előjellel. Az irodalomban gyakran találjuk az (ABX)=AXBX=XAXB értelmezést, amikor tehát a belső pont osztóviszonya negatív, és a külsőé pozitív.

3Tanulságos dolog az osztóviszony értékváltozásának grafikus ábrázolása. Célszerűbb evégből AB egyenest koordinátatengelynek, AB szakaszt egységnek tekinteni. Egy X pontban a tengelyre merőlegest állítunk, arra az (ABX) értekét az AB egységszakaszhoz viszonyított nagyságban, a tengelytől fogva, előjele szerint felmérjük. Az így nyert végpontokat összekötő vonal hiperbola.

4Itt nyilvánvalóan nem az érdekel, hogy ilyen két szakaszt miként kapunk, hanem csak az (ABX)=v kirovásnak megfelelő X pont egyértelműen meghatározott voltát kívánjuk beláttatni. Célszerű b segédegyenesre valamely tetszőlegesen választott egységszakaszt, a-ra pedig az adott v abszolútértékét képviselő hosszúságot felrakni, hogy azok töltsék be BN és AM szerepét. Ez a gyakorlatilag kielégítő eljárás a szó szigorú értelmében nem szerkesztés.