Kezdőlap


Cím:	Az 1955. évi Rákosi Mátyás tanulmányi verseny I. fordulója
Füzet:	1955/május, 130 - 136. oldal	PDF \| MathML
Témakör(ök):	OKTV

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ez idén e verseny március 8-án folyt le az egyes iskoláknál a szokott szabályok szerint: csak a gimnáziumok és az ipari technikumok III. és IV. osztályú tanulói indulhattak. Munkaidő 5 óra. A résztvevők száma ismét meghaladta a 3000-et. Beadtak összesen 223 iskolában 2823 dolgozatot. (Tavaly $209 / 2896$ .) A gimnáziumokra eső rész $164 / 2149$ (tavaly $157 / 2139$ ) még csak igen kicsiny előnyös változást mutat, de az ipari technikumok adataiból: $59 / 674$ a tavalyi $52 / 757$ -tel szemben, már határozottan mutatkozik a $≫$ több iskola kevesebb tanuló $≪$ tendenciája, ami feltétlenül minőségi javulást jelent.
A versenybizottságnak április 6-i javaslata alapján 341 versenyző (a dolgozatot beadók $12, 1 %$ -a) került a döntőbe a tavalyi $287 = 9, 8 %$ -kal szemben. Ez a javulás főleg az ipari technikumok vonalán történt előnyös eltolódásnak köszönhető. Ugyanis amíg tavaly 29 ip. technikumnak 41 tanulója (a dolgozatot beadók $5, 4 %$ -a) került a döntőbe, addig ez idén 33 ip. technikumnak 81 tanulója ( $12, 0 %$ ) nyert jogot a II. fordulóban való részvételre. Részletes adatok megyék és iskolafajok szerint az itt közölt táblázatban találhatók.
A döntőbe került 341 tanuló közül csak 148-an ( $43, 4 %$ ) lapunk feladatmegoldói, ami ismét felderíti azt a sajnálatos tényt, hogy igen sok, matematikában tehetséges, tanuló nem forgatja lapunkat, és megmutatja, mennyire indokolatlan számos iskola teljes passzivitása a $≫$ Középiskolai Matematikai Lapok $≪$ -kal szemben.
Amíg a tavalyi R. M. versenyen helyezést elért 29 III. osztályú tanuló ez idén, kivétel nélkül, mind bekerült a döntőbe, addig a tavalyi Arany Dániel versenyen helyezett 30 II. oszt. tanuló közül 11-nek nem sikerült ezúttal az R. M. verseny II. fordulójába kerülni.
Alább közöljük a kitűzött három feladatot a megoldásokkal együtt.

1. feladat. Adva van valamely mértani sorozat első tagja, utolsó tagja és tagjainak száma. Mekkora tagjainak szorzata?

I. megoldás: Jelöljük a keresett szorzatot

P_{n}

-nel.

\begin{matrix} P_{n} = a_{1} a_{2} ... a_{n} = a_{1} \cdot a_{1} q \cdot a_{1} q^{2} ... a_{1} q^{n - 1} = a_{1}^{n} \cdot q^{1 + 2 + ... + (n - 1)} . \end{matrix}

q

kitevőjében levő számtani sorozat összege

\frac{(n - 1) n}{2}

, és így

\begin{matrix} P_{n} = a_{1}^{n} q^{\frac{(n - 1) n}{2}} = a_{1}^{n} {(q^{n - 1})}^{\frac{n}{2}} . \end{matrix}

(1)

Mivel

a_{1} q^{n - 1} = a_{n}

, azért

\begin{matrix} q^{n - 1} = \frac{a_{n}}{a_{1}}, \end{matrix}

mely értéket (1)-be helyettesítve

\begin{matrix} P_{n} = a_{1}^{n} \frac{{a_{n}}^{\frac{n}{2}}}{{a_{1}}^{\frac{n}{2}}} = {a_{1}}^{\frac{n}{2}} {a_{n}}^{\frac{n}{2}} = {(a_{1} a_{n})}^{\frac{n}{2}} . \end{matrix}

Megjegyzés: Az (1) alatti kifejezés a következőképpen is átalakítható

\begin{matrix} a_{1}^{n} {(q^{n - 1})}^{\frac{n}{2}} = {(a_{1}^{2} q^{n - 1})}^{\frac{n}{2}} = {(a_{1} \cdot a_{1} q^{n - 1})}^{\frac{n}{2}} = {(a_{1} a_{n})}^{\frac{n}{2}} . \end{matrix}

II. megoldás:

\begin{matrix} P_{n} = a_{1} \cdot a_{1} q \cdot a_{1} q^{2} ... a_{1} q^{k - 1} ... a_{1} q^{n - 1} \end{matrix}

(1)

a mértani sorozat tagjait mint tényezőket

a_{n}

-től kezdve fordított sorrendbe írva

\begin{matrix} P_{n} = a_{n} \cdot \frac{a_{n}}{q} \cdot \frac{a_{n}}{q^{2}} ... \frac{a_{n}}{q^{k - 1}} ... \frac{a_{n}}{q^{n - 1}} . \end{matrix}

(2)

(1) és (2) szorzata úgy képezhető, hogy az egymás alatt álló tényezőket páronként összeszorozzuk. Tehát

\begin{matrix} P_{n}^{2} = (a_{1} a_{n}) (a_{1} a_{n}) ... (a_{1} a_{n}) ... (a_{1} a_{n}) = {(a_{1} a_{n})}^{n}, \end{matrix}

amiből

\begin{matrix} P_{n} = \sqrt[]{{(a_{1} a_{n})}^{n}} = {(a_{1} a_{n})}^{\frac{n}{2}} \end{matrix}

Kimutatás az 1955. évi Rákosi Mátyás matematikai verseny I. fordulójáról

megyék és iskolafajok szerint

\begin{matrix} Beadott dolgozatok & Döntőbe került \\ gimnázium & ip. techn. & Összesen & gimnázium & ip. techn. & Összesen \\ Megyék és  Budapest & is & ta & is & ta & is & ta & is & ta & is & ta & is & ta \\ ko & nu & ko & nu & ko & nu & ko & nu & ko & nu & ko & nu \\ la & ló & la & ló & la & ló & la & ló & la & ló & la & ló \\ 1. Baranya & 6^{1} & 117 & 3 & 58 & 9 & 175 & 2^{4} & 6 & 2 & 6 & 4 & 12 \\ 2. Bács-Kiskun & 8 & 80 & 1 & 1 & 9 & 81 & 5 & 10 & 1 & 1 & 6 & 11 \\ 3. Békés & 10 & 93 & 1 & 18 & 11 & 111 & 4 & 6 & ‐ & ‐ & 4 & 6 \\ 4. Borsod & 8 & 95 & 5 & 79 & 13 & 174 & 8 & 20 & 2 & 5 & 10 & 25 \\ 5. Csongrád & 7^{2} & 124 & 3 & 49 & 10 & 173 & 5 & 6 & 2 & 6 & 7 & 12 \\ 6. Fejér & 2 & 25 & 3 & 19 & 5 & 44 & 1 & 4 & 2 & 3 & 3 & 7 \\ 7. Győr-Sopron & 9 & 131 & 4 & 36 & 13 & 167 & 5 & 10 & 1 & 1 & 6 & 11 \\ 8. Hajdu-Bihar & 9 & 108 & 3 & 28 & 12 & 136 & 6 & 11 & 1 & 2 & 7 & 13 \\ 9. Heves & 4 & 46 & 1 & 1 & 5 & 47 & 3 & 8 & 1 & 1 & 4 & 9 \\ 10. Komárom & 8 & 77 & 2 & 7 & 10 & 84 & 4 & 11 & 1 & 1 & 5 & 12 \\ 11. Nógrád & 2 & 15 & 1 & 3 & 3 & 18 & 1 & 1 & 1 & 3 & 2 & 4 \\ 12. Pest & 8 & 65 & 1 & 11 & 9 & 76 & 5 & 6 & 1 & 2 & 6 & 8 \\ 13. Somogy & 4 & 63 & 1 & 20 & 5 & 83 & 2 & 3 & ‐ & ‐ & 2 & 3 \\ 14. Szabolcs-Szatmár & 6 & 93 & 2 & 21 & 8 & 114 & 2 & 2 & 1 & 1 & 3 & 3 \\ 15. Szolnok & 11 & 101 & 2^{3} & 10 & 13 & 111 & 5 & 6 & 1^{3} & 1 & 6 & 7 \\ 16. Tolna & 6 & 73 & ‐ & ‐ & 6 & 73 & 1 & 2 & ‐ & ‐ & 1 & 2 \\ 17. Vas & 9^{4} & 104 & 1 & 3 & 10 & 107 & 5^{7} & 11 & 1 & 2 & 6 & 13 \\ 18. Veszprém & 6 & 94 & 2 & 31 & 8 & 125 & 5 & 14 & 1 & 1 & 6 & 15 \\ 19. Zala & 2 & 18 & 2 & 17 & 4 & 35 & 1 & 1 & 1 & 3 & 2 & 4 \\ Vidék & 125 & 1522 & 38 & 412 & 163 & 1934 & 70 & 138 & 20 & 39 & 90 & 177 \\ 20. Budapest & 39^{5} & 627 & 21 & 262 & 60 & 889 & 33^{8} & 122 & 13 & 42 & 46 & 164 \\ Összesen & 164 & 2149 & 59 & 674 & 223 & 2823 & 103 & 260 & 33 & 81 & 136 & 341 \end{matrix}

^{$^{*}$}
2. feladat. Egy háromszög belsejében felvett tetszőleges ponton át a háromszög oldalaival párhuzamos egyeneseket húzunk. Ezek az egyenesek a háromszög területét hat részre osztják. Mekkora az adott háromszög területe, ha adva van a keletkezett 3 háromszög területe:

t_{n}

t_{2}

t_{3}

I. megoldás: Legyenek a keletkezett részháromszögeknek az adott háromszög

a

oldalával párhuzamos oldalai rendre

a_{1}

a_{2}

a_{3}

és ezen oldalakhoz tartozó magasságok

m_{1}

m_{2}

m_{3}

. Nyilvánvaló, hogy

a_{1} + a_{2} + a_{3} = a

, és az is könnyen belátható, hogy

m_{1} + m_{2} + m_{3} = m

(1. ábra), ahol

m

az adott háromszögnek

a

oldalához tartozó magassága.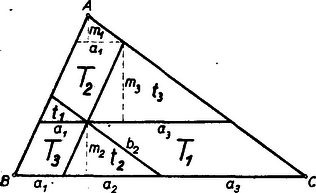

1. ábra

Tehát az adott háromszög területét

T

-vel jelölve

\begin{matrix} 2 T = a m = (a_{1} + a_{2} + a_{3}) (m_{1} + m_{2} + m_{3}) = \\ a_{1} m_{1} + a_{2} m_{2} + a_{3} m_{3} + (a_{1} m_{2} + a_{2} m_{1}) + (a_{1} m_{3} + a_{3} m_{1}) + (a_{2} m_{3} + a_{3} m_{2}) & (1) \end{matrix}

2 t_{1} = a_{1} m_{1}

és

2 t_{2} = a_{2} m_{2}

; e két egyenlőség szorzata

\begin{matrix} 4 t_{1} t_{2} = a_{1} m_{1} a_{2} m_{2} = (a_{1} m_{2}) (a_{2} m_{1}) \end{matrix}

(2)

Mivel a részháromszögek ‐ a szögek egyenlősége miatt ‐ mind hasonlók az adott háromszöghöz, és így egymás között is, azért

\begin{matrix} \frac{a_{1}}{a_{2}} = \frac{m_{1}}{m_{2}}, vagyis a_{1} m_{2} = a_{2} m_{1} . \end{matrix}

Tehát (2) alapján

\begin{matrix} {(a_{1} m_{2})}^{2} = {(a_{2} m_{1})}^{2} = 4 t_{1} t_{2}, \end{matrix}

amiből

\begin{matrix} a_{1} m_{2} = a_{2} m_{1} = 2 \sqrt[]{t_{1} t_{2}}, vagyis a_{1} m_{2} + a_{2} m_{1} = 4 \sqrt[]{t_{1} t_{2}} . \end{matrix}

Ugyanígy mutatható meg, hogy

\begin{matrix} a_{1} m_{3} + a_{3} m_{1} = 4 \sqrt[]{t_{1} t_{3}} és a_{2} m_{3} + a_{3} m_{2} = 4 \sqrt[]{t_{2} t_{3}} . \end{matrix}

Ezen értékeket (l)-be helyettesítve, és 2-vel osztva

\begin{matrix} T = t_{1} + t_{2} + t_{3} + 2 \sqrt[]{t_{1} t_{2}} + 2 \sqrt[]{t_{1} t_{3}} + 2 \sqrt[]{t_{2} t_{3}} = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}

Megjegyzés: Ha a keletkezett 3 paralelogramma területeit

T_{1}

T_{2}

T_{3}

-mal jelöljük, amint azt az ábra mutatja, akkor az ábrából közvetlenül leolvasható, hogy

\begin{matrix} a_{1} m_{2} (= 2 \sqrt[]{t_{1} t_{2}}) = T_{3}, a_{3} m_{2} (= 2 \sqrt[]{t_{2} t_{3}}) = T_{1}, \end{matrix}

és könnyen belátható (kis területi átalakítás után), hogy

\begin{matrix} a_{1} m_{3} = (= 2 \sqrt[]{t_{1} t_{3}}) = T_{2}, \end{matrix}

Eszerint a fenti eredmény a

T = t_{1} + t_{2} + t_{3} + T_{1} + T_{2} + T_{3}

egyenlőség alapján adódik.
Az itt felhasznált összefüggések közvetlen igazolásán (mégpedig a hasonlóság felhasználása nélkül) alapszik a következő megoldás.

II. megoldás: Tekintsük először az ábrának

t_{1}

t_{3}

és

T_{2}

alkotta részét. A betűzést a 2. ábra mutatja.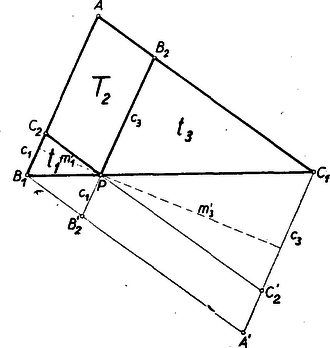

2. ábra

Egészítsük ki az

A B_{1} C_{1}

háromszöget, a

B_{1} C_{1}

oldal felezőpontjára tükrözve, paralelogrammává és hosszabbítsuk meg a

B_{2} P

és

C_{2} P

szakaszokat a paralelogramma szemközti oldaláig. Ekkor

\begin{matrix} B_{1} C_{1} A_{▵} ≅ C_{1} B_{1} A_{▵}^{'}, P B_{1} C_{2 ▵} ≅ B_{1} P B_{2 ▵}^{'}, C_{1} P B_{2 ▵} ≅ P C_{1} C_{2 ▵}^{'} \end{matrix}

és így a

C_{2} A B_{2} P

paralelogramma

T_{2}

területe megegyezik a

B_{2}^{'} A^{'} C_{2}^{'} P

paralelogrammáéval. Az előbbinek

P B_{2} = c_{3}

, oldalához tartozó magassága egyenlő a

t_{1}

háromszög

c_{1}

oldalához tartozó

m'_{1}

magasságával; az utóbbi paralelogramma

P B_{2}^{'} = c_{1}

oldalához tartozó magassága pedig a

t_{3}

háromszög

c_{3}

oldalához tartozó

m'_{3}

magasságával. Tehát

\begin{matrix} T_{2} = c_{3} m_{1} = c_{1} m'_{3}, \end{matrix}

amiből

\begin{matrix} T_{2}^{2} = c_{1} m_{1}' c_{3} m_{3}' = 4 t_{1} t_{3}, vagyis T_{2} = 2 \sqrt[]{t_{1} t_{3}} . \end{matrix}

Hasonlóképpen adódik, hogy

\begin{matrix} T_{1} = 2 \sqrt[]{t_{2} t_{3}}, T_{3} = 2 \sqrt[]{t_{1} t_{2}}, \end{matrix}

és így

\begin{matrix} T = t_{1} + t_{2} + t_{3} + 2 \sqrt[]{t_{2} t_{3}} + 2 \sqrt[]{t_{3} t_{1}} + 2 \sqrt[]{t_{1} t_{2}} = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}

III. megoldás: Legegyszerűbben úgy jutunk célhoz, ha felhasználjuk azt az ismeretes tételt, mely szerint hasonló háromszögek területei úgy aránylanak egymáshoz, mint a megfelelő oldalak négyzete.
Tehát

\begin{matrix} \sqrt[]{t_{1}} : \sqrt[]{T} = a_{1} : (a_{1} + a_{2} + a_{3}), \\ \sqrt[]{t_{2}} : \sqrt[]{T} = a_{2} : (a_{1} + a_{2} + a_{3}), \\ \sqrt[]{t_{3}} : \sqrt[]{T} = a_{3} : (a_{1} + a_{2} + a_{3}) . \end{matrix}

Összeadva

\begin{matrix} \frac{\sqrt[]{t_{1}}}{\sqrt[]{T}} + \frac{\sqrt[]{t_{2}}}{\sqrt[]{T}} + \frac{\sqrt[]{t_{3}}}{\sqrt[]{T}} = \frac{a_{1} + a_{2} + a_{3}}{a_{1} + a_{2} + a_{3}} = 1, \end{matrix}

ahonnan,

\begin{matrix} \sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}} = \sqrt[]{T}, \end{matrix}

vagyis

\begin{matrix} T = {(\sqrt[]{t_{1}} + \sqrt[]{t_{2}} + \sqrt[]{t_{3}})}^{2} . \end{matrix}

3. feladat. Két munkás A és B valamely rájuk bízott munkát a következőképpen végzett el. Először csak A dolgozott

\frac{2}{3}

annyi ideig, mint amennyi idő alatt B egyedül elvégezné az egész munkát. Azután B felváltotta A-t és befejezte a munkát. Ilyen módon a munka 2 órával több időt vett igénybe, mintha együtt fogtak volna hozzá és együttesen végezték volna el. Ha együtt dolgoztak volna az utóbbi módon, akkor A fele annyi munkát végzett volna, mint amennyit ténylegesen B-re hagyott. Hány óra alatt végezné el a munkát A, illetőleg B egyedül?

I. megoldás: Legyen az adott munka egységnyi. Tegyük fel, hogy a munkát

A